基于改进证据理论和检测信息的混凝土桥梁服役状态评估分析
任荣明 谭海立 罗月静



摘要:为解决传统证据理论方法证据冲突的问题,文章结合模糊层次分析法与证据理论,提出了改进的证据理论方法,建立了相应的评定指标体系和评定准则,并结合某混凝土桥梁工程实例,与传统模糊层次分析法进行对比分析,验证了所提方法的优越性。
关键词:在役混凝土桥梁;改进证据理论;桥梁检测;服役状态评定
文献标识码:U448.33-A-36-120-4
0 引言
随着桥梁老化现象加剧以及“危/病桥”数量的快速增加,在役桥梁的状态评定研究越发重要。目前,国内外服役桥梁技术状况评定规范中使用较多的方法主要包括分层综合评定法与单项指标控制法相结合的评估方法,以经验分析法为主,试验分析法为辅,基于实测或监测数据的可靠性分析法为补充的多方法综合运用的评估方法。上述不同的桥梁状态评定方法具有各自的优点和不足,如我国《公路桥梁技术状况评定标准》中的评定方法虽然流程较为简单、运用比较广泛,但该法主要基于实桥检测信息进行定性评价,主观经验成分较大[1]。一些学者对其他桥梁评定方法展开了积极探索。刘来君等[2]结合AHP法和改进贝叶斯理论建立了一种新颖的服役桥梁状态评定方法,该法不仅能合理地利用历史评定信息对桥梁实际状态进行快速评估,还能大大减少评定过程产生的费用;Sasmal和Ramanjaneyulu[3]基于层次分析法给出了服役桥梁技术状况评定的系统步骤和相应评估公式,提出了桥梁或构件维修优先级的确定方法,该方法能帮助桥梁管理或决策者解决与桥梁维修相关的优先级和资金决策问题,其将结构健康监测数据与可靠性分析程序相结合。
目前,虽然有些学者已经将证据理论应用到了桥梁服役状态的评定当中,如王应明等[4-5],但是却鲜有学者研究证据融合过程中可能造成的证据冲突现象,以及此计算方法在混凝土桥梁服役状态评定中的应用。因此,本文在现有研究成果基础上,将改进的证据理论与模糊层次分析法相结合,并融入实桥检测数据,建立相应的桥梁评价体系和模糊评价集,将本文提出的方法应用于实桥的服役状况评估,同时与传统模糊综合评判法进行对比分析,验证了该改进证据理论的优越性。
1 证据理论和模糊层次分析法
1.1 模糊层次分析法
由于具有理论完备、结构严谨、使用简洁的特点,模糊层次分析法(FAHP)已被广泛用于中小型桥梁的技术状况评定。现有不少学者对FAHP法的定义和计算方法展开了深入研究[6-7],此处不再详细介绍。在本文中,该法主要包含以下三个步骤:(1)建立完整的状态指标体系;(2)根据专家给出的各状态指标之间的重要性信息构造两两比较矩阵,并对上述所有矩阵进行一致性检验,以验证各指标重要性之间的协调性,确保指标权重体系具有较好的稳健性;(3)通过计算优先权重、优先权重去模糊化以及对去模糊化后的权重进行标准化来获得各状态指标的最终权重。
1.2 改进证据理论
证据理论中识别框架Θ={A1,A2,…,An},证据的基本概率赋值函数为
mi(Aj),表示证据mi对命题Ai的信任度,合成公式如式(1)所示:
m(A)=11-K∑∩Aj=A∏1≤j≤nmi(Aj),AΘ,A≠Φm(Φ)=0,其他
(1)
式中,K=∑∩Aj=Φ∏1≤j≤nmi(Aj)表示冲突权值,反映了证据的冲突程度。当K值为1时,传统证据理论方法不再适用,因此本文对冲突证据修正以提高桥梁评估精度。辨识框架中坐标采用证据的基本概率函数(BPA)赋值,将证据转化成该框架中的一组向量
mi=(mi(A1),mi(A2),…,mi(An))T。为避免赋值大小顺序对证据产生冲突,采用文献[8]中相似度方法重新定义,如式(2)所示:
Simij=αcosmi,mj+β
Simseqmi,mj
(2)
式中:cos(mi,mj)为证据向量mi、mj
之间的余弦相似度;cos(mi,mj)=miTmj/(miTmi)(mjTmj);
Simijseq=1-δij∑kikjp=1Rpi-Rpj2/∑nl=1n+1-2l2。在识别框架Θ下,针对N个证据向量中第i个证据向量mi的平均相似度为:
Simi=1N-1∑Nj=1,i≠jSimij
(3)
由此可得确定证据mi的相似度,经修正冲突矩阵后,得到基本概率赋值:
m′i(Aj)Crdi·mi(Aj),Aj≠ΘCrdi·mi(Θ)+1-Crdi,Aj=Θ
(4)
对证据向量mi中原始数据mi(Aj)按式(5)进行修正:
mi(Aj)=miAj,Confi≤τm′iAj,Confi>τ
(5)
2 桥梁评价体系
在桥梁评价工作中,为了得到正确、合理的桥梁评价信息,就必须建立正确的评价体系。一般应符合下列条件:完备性、唯一性、代表性、简洁性。
依照混凝土桥梁的特点,可将桥梁評价体系按对象划分为三个层次。顶层待评估参数反映了桥梁评价的最终结果。中间评价层的待评估参数可依照桥梁的主要构件进行划分,分别是:上部结构、下部结构、附属构造物、支座及其他四个部分。底层待评估参数则可按照代表性进行划分,一般可划分出多个。对桥梁结构主要构件的描述,可以是定性的或者是定量的,因此可建立如图1所示的桥梁评价体系。
3 桥梁评估隶属度函数及评估准则
参考文献中的做法[9-10]和桥梁专家的经验与认知,利用概率统计规律进行统计分析,且依照混凝土梁桥的分级标准和与此相关的隶属度函数,根据形式的不同,可将隶属函数主要划分为:正态分布型、矩形分布、梯形分布、三角分布等。由于梯形隶属度函数计算过程简洁明了,且依照分级标准能够将待评估参数的等级隶属关系清晰完整地表达出来,适用于大多数工程实际。因此本文采用梯形隶属度函数来研究待评估参数的模糊隶属性。
对于越大越优的待评估参数,当评估级别为1时,隶属度函数为式(6):
I1=
0max(H2)
x-max(H2)min(H
1)-max(H2)max(H2)
(6)
当评估级别为2、3、4时,隶属度函数可依照式(7)计算:
Ik=00
(7)
则待评估参数隶属于级别5时,可建立相应的隶属度函数为式(8):
I5=1x
(8)
上式中,Hk(k=1,2,3,4,5)为相应评估级别的分级标准区间。针对越小越优指标则将上述隶属函数max与min,<(≤)和>(≥)进行两两互换即可。
依照规范[11]建立服役桥梁状态评定标准,划分为五个评级类别,分别为:1类、2类、3类、4类、5类,并建立对应的模糊集:
H={H1,H2,H3,H4,H5},其含义分别表示为:良好、较好、较差、很差、危险。各评定分级及代表含义如表1所示。
在评价过程中,一部分底层待评估参数可以采用实际测量或计算结果进行定量评定,而另一部分底层待评估参数只能采用定性描述进行分级评定。为了能够对五类桥服役状况进行比较清晰明了的描述,评定准则的建立本文则依照模糊划分原则进行处理。评价体系中底层待评估参数评定标准区间及其含义如表2所示。
4 现场检测结果
4.1 主梁的检测
抗弯可靠度:基于测试数据,利用《结构可靠度理论》[12]中的方法得到此桥现有服役年限的抗弯可靠度为4.07。结构表观损伤:经检测分析发现,表观蜂窝以及混凝土剥落等现象不明显,但梁体多处出现裂缝破碎现象,与设计时的主梁面积相比较,经统计分析损伤率大致在16%左右。普通钢筋锈蚀:使用GXY1型钢筋锈蚀测量仪进行测量取值,得到各测区普通钢筋电位水平的均值大致为-297.84 mV。
4.2 下部结构的检测
普通钢筋锈蚀:使用GXY1型钢筋锈蚀测量仪进行测量取值,因此下部结构各测区普通钢筋电位水平的均值大致为-304.41 mV。混凝土强度:采用回弹法对下部结构混凝土的实体强度进行推定,计算其平均换算强度,然后与极限抗压强度相比较,得出下部结构的混凝土强度匀质系数为0.947。墩台基础裂缝:墩台基础的最大裂纹宽度可采用裂缝宽度仪测出,测得其值为0.16 mm。
4.3 支座及其他
支座狀态:经过仔细检查支座完好、清洁、转动正常,未出现垫板锈蚀、老化和支座处混凝土剥落的现象,评价结果为良好。
4.4 附属构造物
桥面铺装缺损率:对桥面铺装而言,局部有油污、坑槽,铺装层表面不存在较严重的龟裂现象,但个别位置存在表面破碎现象。经统计分析,桥面铺装缺损水平大致在19.3%左右。人行道及栏杆缺损:对栏杆、护栏而言,约有长度为护栏总长0.8%的护栏存在局部变形或冲撞引起的损坏,且少数栏杆存在防护漆脱落现象。照明系统损坏:对照明系统而言,全桥仅3个灯泡损坏,但有5个灯柱出现轻微锈蚀,且其中1个灯柱歪斜不正,仅占总体的1%左右。
5 桥梁服役状态评价分析
为了对某桥的服役状态进行准确的评价,邀请从事桥梁检测人员、业内桥梁专家、工程监理人员以及桥梁维修加固技术人员共计8人组成专家评价小组,根据相关规范对此桥的实际病害情况进行系统的评估。经过收集并整理评价小组各位专家的评价建议,在争取各位专家的同意后,建立如表3~7中所示的各个层次的模糊判断矩阵和权重值。
根据检测结果,计算得到各个中间待评估参数的隶属度矩阵为:
上部结构:R1=00.850.150000.3330.6670000.7170.28300
下部结构:R2=00.60.40000.5640.4360000.850.15000.20.8000
支座及其他:R3=00.4360.5640010000
附属构造物:R3=000.5010.4990000.920.08000.4440.5560010000
因此,可以得到中间评估层的各个待评估参数的基本信度分配函数矩阵为:
M=ΘHⅠHⅡHⅢHⅣHⅤ0.81500.1290.0560000.0390.7060.2550000.3670.2760.3570000.1950.1380.5360.1310
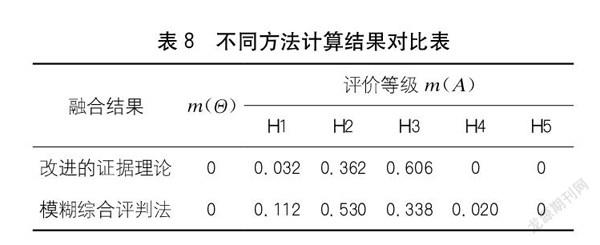
进行证据理论的融合计算,并且和模糊综合评判法对比。计算结果如后页表8所示。
根据最大隶属度原则,对两种计算方法所得结果进行比较。从表8中可以看出,模糊综合评判法计算所得的评估结果均指向2类桥,改进的证据理论指向3类桥。造成这一现象的原因是由于模糊综合评判法不能够很好地解决评价指标中不确定的因素,同时此评估方法过于依赖于权重值的大小。而本文所提出的改进证据理论能够充分考虑证据间的冲突特性,将高冲突证据给予合理的修正,提升了评价结果的可信性。从此评估结果得知此桥为较差的服役状态,因此应提醒相关单位做好桥梁加固措施。
6 结语
混凝土桥梁服役状态的评估是一项复杂的多指标评价问题。本文将模糊层次分析法与证据理论结合,提出了改进的证据理论方法,建立了相应的评定指标体系和评定准则,结合现场桥梁检测结果,以某混凝土实桥服役状态评定为例对所提出的方法进行了阐述,与传统模糊层次分析法进行对比验证了方法的优越性。本文所提方法可为在役混凝土桥梁维修加固决策提供理论依据,在具体的桥梁检测评定当中有着较为广泛的应用前景。
参考文献
[1]JTG/T H21-2011,公路桥梁技术状况评定标准[S].
[2]刘来君,吴 多,张 夏,等.改进贝叶斯方法在桥梁状态评估中的应用[J].长安大学学报(自然科学版),2017,37(6):47-53.
[3]Sasmal S,Ramanjaneyulu K.Condition evaluation of existing reinforced concrete bridges using fuzzy based analytic hierarchy approach[J].Expert Systems with Applications,2008,35(3):1 430-1 443.
[4]Wang Yingming,Elhag T M S.Evidential reasoning approach for bridge condition assessment [J].Expert Systems with Applications,2008,34(1):689-699.
[5]王 涛,王应明.基于证据理论的不同形式偏好信息群决策方法研究[J].情报探索,2012(3):1-3.
[6]Mosadeghi R,Warnken J,Tomlinson R,et al. Comparison of Fuzzy-AHP and AHP in a spatial multi-criteria decision making model for urban land-use[J].Computers,Environment and Urban Systems,2015(49):54-65.
[7]張征昀,彭步新,王子健,等.基于改进证据理论与IFAHP的预应力混凝土梁桥状态评估[J].公路与汽运,2020(6):135-139.
[8]田林钢,靳聪聪,巴 超.改进的模糊层次分析法在海堤工程安全评价中的应用[J].武汉大学学报(工学版),2013,46(3):317-320.
[9]刘文龙.基于不确定型层次分析法桥梁安全性评估研究[D].武汉:武汉理工大学,2005.
[10]韩文学.基于AHP的模糊综合评价在混凝土桥梁评估中的应用[D].南宁:广西大学,2007.
[11]JTG H11-2018,公路桥涵养护规范[S].
[12]赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000.
收稿日期:2021-03-08
作者简介:
任荣明(1983—),高级工程师,主要从事桥梁设计及研究工作;
谭海立(1985—),硕士,高级工程师,主要从事桥梁设计及研究工作;
罗月静(1970—),博士,教授级高级工程师,主要从事结构检测与加固设计及课题研究工作。

