基于无迹卡尔曼滤波的火箭弹姿态估计

许立松,马国梁,闻 泉,王雨时

(南京理工大学 1.机械工程学院;2.能源与动力工程学院,江苏 南京 210094)

随着外弹道学的发展,对制导弹药的姿态测量提出了新的要求。大量程微机电(micro electro mechanical systems,MEMS)陀螺的出现为解决高转速测量问题提供了途径,通过MEMS陀螺的角速率测量信息进行捷联解算可以得到弹丸飞行姿态,但随着时间增加会出现误差累积的问题,因此一般将GPS与惯性器件进行组合[1-2],通过Kalman滤波获得飞行姿态的估计值。

Kalman滤波方法于1960年被提出,在其基础上发展了扩展卡尔曼滤波(extended Kalman filter,EKF)、无迹卡尔曼滤波(unscented Kalman filter,UKF)、粒子滤波(particle filter,PF)等一系列滤波方法[3-4]。迭代方法[5]和自适应算法[6]的加入进一步提升了滤波效果,神经网络[7]等人工智能技术也在滤波领域发挥了很大的作用。

国外一直致力于制导弹药姿态估计方面的研究[8-11]。文献[11]采用了EKF方法对双旋弹丸进行姿态估计;文献[12]针对炮射弹丸将卡尔曼滤波与多维标度(multi-dimensional scaling,MDS)相结合,提高了位置测量的鲁棒性。国内也有相应的研究,文献[13]利用UKF方法辨识弹道模型,预报弹道落点;文献[14]将UKF方法加以改进,降低了弹丸射程修正的误差;文献[15]结合EKF建立了固定鸭舵双旋弹的实时位置和速度估计方法。可以看到,多数研究集中在弹丸位置及速度参数的估计,部分弹丸姿态估计的研究主要使用EKF方法。使用EKF需要对系统进行线性化处理,而本文所述的火箭弹滚转角速率较高,是状态变化较快的强非线性系统,因而线性化模型导致的精度丢失会导致滤波误差的进一步加大。UKF方法实际上属于粒子滤波器的一种,也被称为Sigma点滤波器。UKF方法最大的特点是采用无迹变换来估计非线性变换的均值和方差,其计算复杂程度与扩展卡尔曼滤波相当,有研究表明,在对飞行器气动参数辨识效果的比较中,UKF在辨识精度和收敛性上都优于EKF。在以非线性系统模型为基础的滤波算法中,UKF的计算量相对较小,随着现今嵌入式系统计算能力的提升,基于UKF算法的实时嵌入式滤波有望实现工程化应用,因而选用UKF滤波方法进行组合滤波,并与EKF方法的滤波效果相对比,进行更深层次的讨论。

本文以某尾翼稳定火箭弹为研究对象,测量器件包括三轴角速率陀螺、三轴加速度计和GPS组件,陀螺和加速度计以捷联方式安装于弹体,能够在弹丸飞行过程中测得弹体坐标系下的三轴角速率及三轴加速度。针对其姿态估计的滤波问题,以姿态角、位置、速度参数作为状态变量,建立了火箭弹运动参数的捷联惯性解算模型,以GPS的位置和速度测量值作为输出变量,构成组合滤波模型。分别通过EKF和UKF滤波方法对飞行姿态进行估计,仿真结果表明,UKF组合滤波方法的滤波性能更加优良,其俯仰角、偏航角估计误差均方根相比EKF降低了一半,滚转角估计误差均方根降低了三分之二,满足姿态估计的需求。

1 组合滤波模型

1.1 姿态角及坐标系定义

为了描述火箭弹的飞行姿态,引入飞行力学中的姿态角概念:俯仰角ϑ,偏航角ψ,滚转角γ。地面坐标系Axyz和弹体坐标系Ox1y1z1定义方式如文献[16]所述。地面坐标系Axyz先绕Ay轴顺时针旋转ψ角,形成坐标系Ax0yz0,坐标系Ax0yz0再绕Az0轴顺时针旋转ϑ角形成坐标系Ax1y0z0,坐标系Ax1y0z0再绕Ax1轴顺时针旋转γ角形成坐标系Ax1y1z1,坐标系Ax1y1z1平移至弹丸质心形成弹体坐标系Ox1y1z1。用俯仰角ϑ和偏航角ψ可以确定弹轴在地面坐标系中的指向。

1.2 捷联惯性解算模型

描述弹丸运动的基本参数除了姿态角外,还包括飞行速度及弹丸的位置坐标,共9个运动参数,根据飞行力学及惯性导航知识[16],以差分形式写出捷联惯性解算方程组为

(1)

式中:Ts为采样周期;上标k表示离散时刻序号;ωx1,ωy1,ωz1分别为弹体坐标系下三轴角速率;ax1,ay1,az1分别为弹体坐标系下三轴加速度分量;vx,vy,vz分别为弹丸对地飞行速度在地面发射坐标系下的三轴分量;x,y,z分别为弹丸质心位置在地面发射坐标系下的三轴分量。

根据测量特性,认为三轴陀螺和加速度计的测量误差由系统误差和随机误差构成,以x1轴陀螺为例,测量模型可表示为

(2)

最终取状态向量为

X=(ϑψγvxvyvzxyz
εgx1εgy1εgz1εax1εay1εaz1)T

(3)

式中:εgx1,εgy1,εgz1为三轴角速率陀螺的系统误差分量;εax1,εay1,εaz1为三轴加速度计的系统误差分量。以x1轴陀螺为例,认为系统误差变化缓慢甚至不随时间变化时,其变化方程可描述为

(4)

对于y1,z1轴陀螺和三轴加速度计的系统误差,状态方程形式与式(4)一致,不再赘述。

根据Kalman滤波理论,式(1)和式(4)构成了状态方程,而地面坐标系下的速度测量值和位置测量值都可以由GPS测量值通过坐标转换得到,观测向量可表示为

Z=(vxvyvzxyz)T+V

(5)

式中:V=(ηvxηvyηvzηxηyηz)T为观测噪声向量,各元素分别表示地面坐标系下速度分量和位置分量的随机观测噪声。

2 EKF滤波方法的实现步骤

组合测姿系统的状态方程形式上较为复杂,采用扩展卡尔曼滤波方法,需先将其线性化,并计算雅可比矩阵。

对于此非线性系统,其状态方程和观测方程可写为

(6)

式中:U为控制向量,W=(ηgx1ηgy1ηgz1ηax1ηay1ηaz1)T为过程噪声,V为观测噪声向量,下标k表示离散时刻序号,其线性化表示为

(7)

(8)

(9)

EKF的实现步骤如下。

①计算相应雅可比矩阵。

②时间更新:

(10)

(11)

③测量更新并计算后验状态估计和状态协方差阵:

(12)

(13)

重复以上步骤,即可计算下一时刻的状态估计值。

3 UKF滤波方法实现步骤

根据UKF基本理论,对于状态方程组(1)和方程组(4),定义增广状态向量为

(14)

式中:W为过程噪声向量,各元素分别表示三轴陀螺和三轴加速度计的随机测量噪声。令过程噪声协方差阵为Q,观测噪声协方差阵为R,状态协方差阵初值记为P0。用χ表示Sigma点对应的变量,令χX为状态向量对应的Sigma点向量,χW为过程噪声向量对应的Sigma点向量,χV为观测噪声向量对应的Sigma点向量,对照增广状态向量的定义方式,定义增广Sigma点向量为

(15)

UKF算法的实现步骤如下。

②按下式计算Sigma点向量:

(16)

式中:α,κ为可以进行设置的滤波器参数;N为增广状态向量维数。

(17)

(18)

(19)

(20)

(21)

⑤求取滤波器增益矩阵,计算后验状态估计和状态协方差阵:

(22)

(23)

(24)

⑤完成后,返回②,计算下一时刻的状态估计值。可以看出UKF与传统Kalman滤波器的区别主要在于状态协方差阵的计算方法不同。

UKF算法中用到的有关参数选择情况如下。

选择κ≥0可以保证协方差阵的正半定性,本文中取κ=0;

选择0≤α≤1,α控制Sigma点的分布范围,一般选一个较小正数,以避免强非线性时的局部采样效应,本文中取α=0.001。

本文假设测量噪声满足高斯分布,参数的优化取值为2,而参数λ=α2(N+κ)-N。

4 仿真分析

以某火箭弹为研究对象,进行六自由度弹道仿真计算,并分别使用惯性解算、EKF组合滤波和UKF组合滤波的方法对全弹道过程进行姿态估计。火箭弹初始质量50 kg,推力持续2.5 s。主要仿真条件:初速为44.969 7 m/s,射角为45°,初始滚转速率为31.73 rad/s,初始偏航速率为2 rad/s。

计算结果表明该弹丸最大转速达到30 r/s,最大马赫数3.2。在生成各测量器件的仿真测量值过程中,惯性器件的采样周期选为2 ms,假定随机噪声均满足高斯分布。其中x1轴陀螺随机误差的标准差为5(°)/s,系统误差10(°)/s,y1、z1轴陀螺随机误差的标准差为5(°)/s,系统误差3(°)/s,x轴加速度计随机误差的标准差为10×10-3g,系统误差为100×10-3g,y、z轴加速度计随机误差的标准差为5×10-3g,系统误差为50×10-3g。地面坐标系下三轴速度测量值的随机误差的标准差为0.1 m/s,三轴位置测量值的随机误差的标准差为5 m,不考虑速度和位置的系统误差。

首先考虑仅采用惯性解算的方式获取俯仰角和偏航角,假设俯仰角、偏航角初始对准误差均为2°,滚转角的初始对准误差为5°。通过惯性解算可以获得全弹道的俯仰角、偏航角和滚转角。

惯性解算结果与弹道仿真值的曲线对比如图1和图2所示。

图1 偏航角惯性解算曲线与真值对比曲线

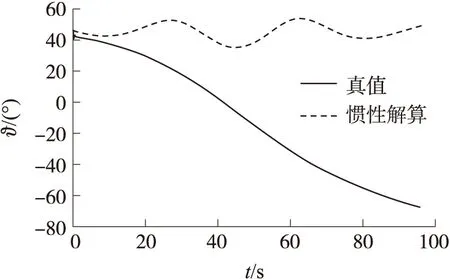
图2 俯仰角惯性解算曲线与真值对比曲线

可以看出,由于积累误差的影响,惯性解算在弹丸飞行几秒内就很快发散,与真值相差较大。

图3～图8为全弹道下各姿态角真值与EKF和UKF滤波估计值的对比曲线,为了便于观察,将俯仰和偏航角的对比曲线分时间段展示。滚转角变化剧烈,亦取其中一段时间内的数据进行观察。

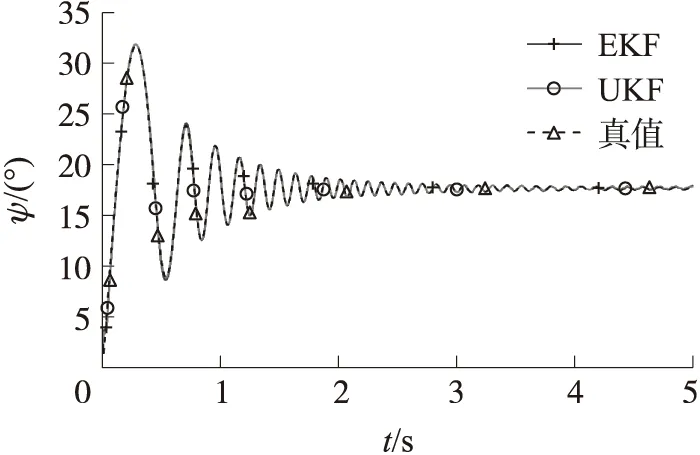
图3 偏航角对比曲线(0～5 s)

图4 偏航角对比曲线(5 s以后)

图5 俯仰角对比曲线(0～5 s)

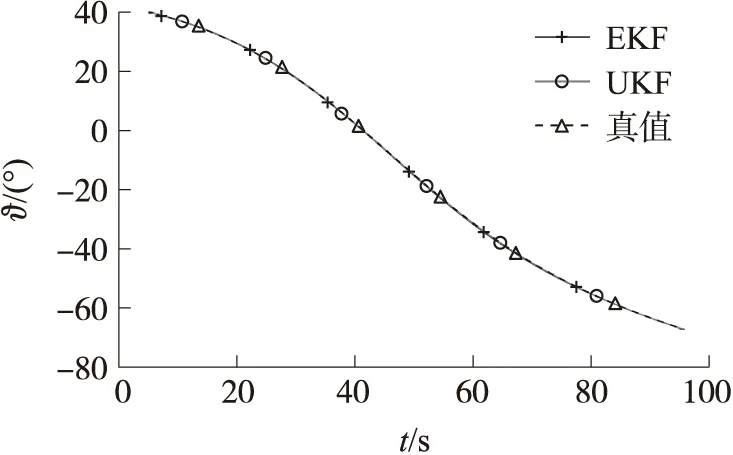
图6 俯仰角对比曲线(5 s以后)

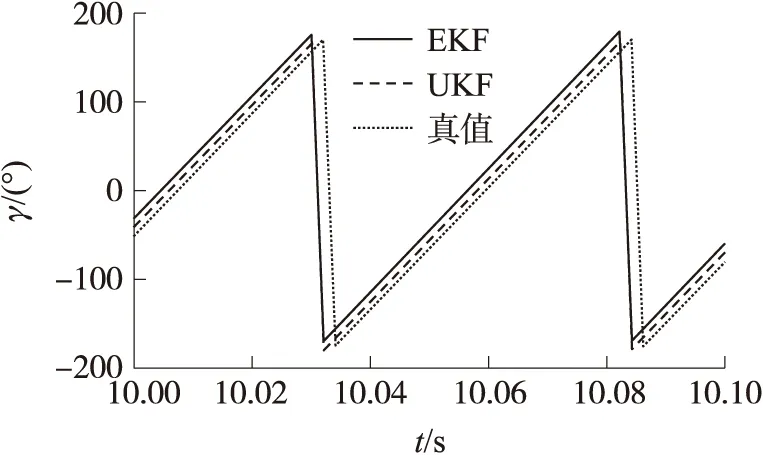
图7 滚转角对比曲线(10～10.1 s)

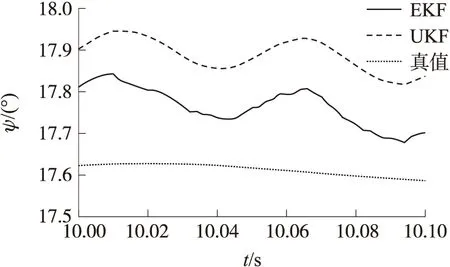
图8 偏航角对比曲线(10～10.1 s)

两种滤波方法下的各姿态角估计误差(Δψ,Δϑ,Δγ)曲线如图9～图11所示。结合表1和表2中数据可以观察到,在俯仰角和偏航角的滤波估计上,EKF和UKF方法的误差都较小,最大误差相当,因而从两者与真值曲线的对比图可看出差距不大,但从误差曲线可以看到,UKF的估计误差明显降低,由表中数据可得其误差均方根较EKF降低了一半。在滚转角的估计上,EKF滤波结果已经完全无法满足测量需求,而UKF方法的估计精度大幅提升,其误差均方根相比EKF降低了三分之二。图中的俯仰角、偏航角的估计值曲线呈波动状,而滚转角的估计曲线较为平滑,原因在于快速变化的滚转角会对俯仰角、偏航角的估计产生影响,从图7与图8可以看到,相同的时间段下,其变化的趋同性是很明显的。当竖直坐标轴范围较小,同时坐标横轴跨度较大,曲线便呈现出了较强的波动性。

图9 EKF和UKF滤波后偏航角估计误差曲线

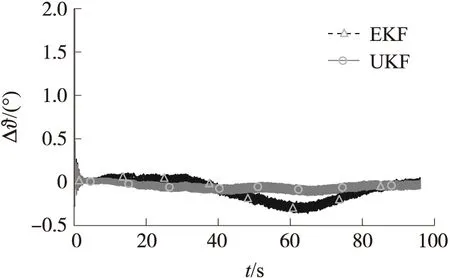
图10 EKF和UKF滤波后俯仰角估计误差曲线

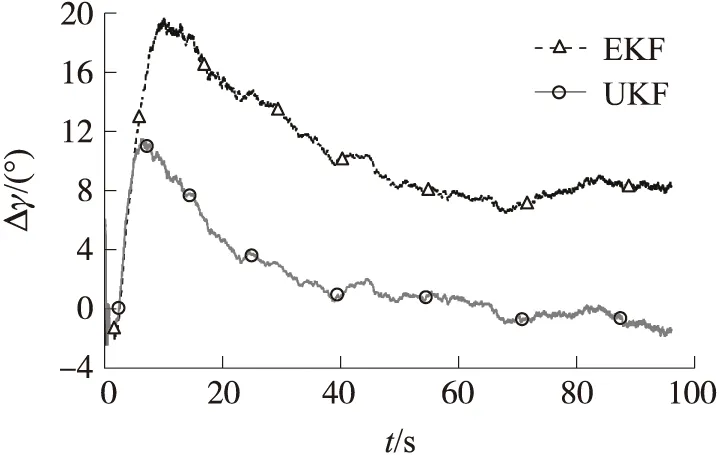
图11 EKF和UKF滤波后滚转角估计误差曲线

表1 滤波估计最大误差

表2 滤波估计误差均方根

产生这些差异的原因在于EKF对模型的线性化使得EKF的先验估计与真值差距较大,在相同的测量噪声设定下,使用无迹变换的UKF没有状态转移模型上的精度损失,显然具有更小的方差分布。随着火箭弹转速的提升,相同的滤波周期下带来的是滚转角更大的变化尺度,从而随着前期的误差积累集中爆发。UKF更高的模型精度同时意味着其收敛速度会优于EKF,这一点在图10也有很好的体现,可以看到UKF的误差拐点先于EKF出现。

5 结束语

本文以姿态角、位置、速度参数作为状态变量,建立了弹丸运动参数的捷联惯性解算模型,对比了EKF和UKF方法的滤波效果。仿真结果验证了UKF组合滤波方法的有效性,其俯仰角、偏航角估计误差均方根相比EKF降低了一半,滚转角估计误差均方根降低了三分之二。

本文的UKF组合滤波方法仍有一定的不足,其对滚转角的跟踪精度尚不能达到同其余两轴相当的程度,如何进一步改进滤波效果并使其适用于运动状态变化更快的制导弹药及常规弹药,都有待进一步研究。