代价敏感组合旋转森林用于脑卒中数据分类

梅晓碧，张雪英+，李凤莲，胡风云，贾文辉

(1.太原理工大学 信息与计算机学院，山西 太原 030024； 2. 山西省人民医院 神经内科，山西 太原 030012)

0 引 言

经颅多普勒超声(Transcranial Doppler，TCD)可以帮助临床医生诊断狭窄、硬化等引起的颈动脉血管疾病，是脑卒中早期筛查诊断的重要依据[1-3]。本文在TCD数据基础上，扩充构建了新的组合特征，利用机器学习方法来挖掘TCD数据中的潜在信息，可以辅助医生更快速、准确地做出诊断。

现实生活中的许多问题都是实例相关的代价敏感问题[4]，近年来它受到越来越多的关注[5-7]，但将实例相关代价引入到脑卒中分类问题中的研究几乎未见报道。Bahnsen等[4]提出了实例相关的代价敏感决策树算法，并对应提出了Savings成本节约量评估指标，取得了可观的成本节约效果。最近，Zelenkov等在Bahnsen的基础上提出了代价敏感决策树的boosting集成算法[5]，进一步提升了成本节约量。旋转森林(rotation forest，ROF)[8]是一种集成分类算法，其核心是利用主成分分析(principal component analysis，PCA)对数据进行特征变换，旨在增加基分类器的多样性。该算法已被广泛应用于各个领域，并表现出了优越的性能[9-11]。

脑卒中TCD数据具有显著的非平衡特性和实例相关代价敏感特性，本文根据脑卒中疾病的特性设计了脑卒中代价矩阵，并用于脑卒中分类模型的构建。同时受文献[9-11]启发，本文提出了一种组合旋转森林框架。将组合旋转森林与实例相关代价敏感问题结合进行TCD非平衡数据的分类研究，并与已有的方法进行比较，验证了本文算法的有效性。

1 实例相关代价敏感的理论基础

1.1 实例相关代价函数

给定训练数据集X，其含有N个实例，每个实例有n个特征，定义X={(xi,yi),i=1,…,N}，xi是n维特征空间X的一个实例，yi∈Y={0,1} 是实例xi的类别标签，标签yi=1对应于少数类(即正类)，yi=0对应于多数类(即负类)。

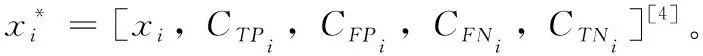
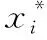
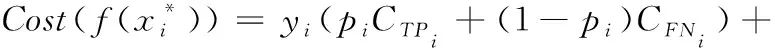
(1)

那么，集合X的总代价为

(2)

1.2 实例相关代价敏感决策树(ECSDT)

本文采用实例相关代价敏感决策树(example-depen-dent cost-sensitive decision tree，ECSDT)[4]作为基分类器，在构建决策树时，采用基于实例成本的节点分割准则，将不同实例的不同成本引入决策树的生成阶段。不同于传统决策树采用信息熵、基尼系数等度量方法，ECSDT使用基于实例成本的不纯度度量方法，考虑每个实例的成本矩阵，旨在衡量分割准则在降低成本方面的表现，而不只是提高准确率。

Cost(f0)表示分类器f将节点中所有的样例分为正常人所造成的损失，Cost(f1)表示分类器f将节点中所有的样例分为脑卒中患者所造成的损失，ECSDT采用两者中的较小值来定义基于成本的不纯度度量

Ic(X)=min{Cost(f0(X)),Cost(f1(X))}

(3)

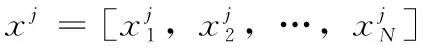
(4)

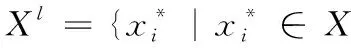
2 特征构建及代价矩阵设计

本文首先根据脑卒中疾病特点，对脑卒中TCD数据进行特征构建，更好挖掘数据信息；然后根据脑卒中的实例相关代价敏感特性设计了针对脑卒中疾病的代价矩阵，将实例相关代价引入到脑卒中TCD数据分类问题中。

2.1 特征构建

本文使用的脑卒中TCD数据均来自山西省人民医院神经内科，其中1248例正常人、553例硬化患者、265例狭窄患者，可见不同病症患者TCD数据量同健康个体TCD数据量之间存在着非平衡关系。每个实例有17维特征。以往的研究[3]只使用了仅有的17维特征，未对特征进行深入的挖掘和研究，本文根据已有的血流特征，构建两组共8维组合特征，包括收缩期最大流速与舒张末期流速的比值S/D；左右两侧动脉血流速度的对称度 |L-R|， 构建的组合特征见表1。其中S/D可评估血管顺应性和血管弹性； |L-R| 可评估左右两侧脑动脉的差别。将组合得到的8维特征加上原始17维特征得到25维特征。

2.2 设计脑卒中分类代价矩阵

脑卒中的分类诊断问题，是与实例相关的代价敏感问题。如果未能成功预测出脑卒中患者，患者会因为病情被延误，错过最佳的预防或治疗时机，从而面临巨大的医疗开销甚至是付出生命的代价。由此造成的后果因人而异，其中年龄是导致各实例代价差异较大的一个关键因素。因为随着年龄的增长，身体各方面机能会有所下降，患者的致残甚至致死的风险会更大，而且还会加大治愈的难度，因此本文将根据不同年龄段的致死率和致残率设计代价矩阵。

首先将每个实例正确分类的代价为0，CTPi=CTNi=0； 然后假定去医院做一次检查的费用为Cti，则将正常人预测为病人的代价CFPi都为Cti；将病人预测为正常人的代价CFNi因人而异，而且大于将正常人预测为病人的代价，即CFNi>CFPi， 本文定义CFNi=Ui·ri·Cti， 其中Ui为数据

表1 脑卒中TCD数据原始特征及组合特征

的不平衡度，ri为实例对应年龄段的致残率和致死率之和。设计的脑卒中代价矩阵见表2。

表2 脑卒中代价矩阵

3 实例相关代价敏感组合旋转森林ECS_CROF

传统的旋转森林采用PCA进行特征映射，旨在增加基分类器的多样性。在此基础上，本文引入有监督的LDA进行特征映射，旨在增加基分类器多样性的同时提升其准确性，此外考虑到不同的特征空间具有不同的表征能力，本文还考虑了原始的特征空间。这样针对每个基分类器，根据3个不同的特征空间训练出3个独立的子分类器，进一步提高组合旋转森林的多样性。

3.1 PCA用作特征映射

PCA是一种无监督的特征变换技术，可使得投影后的数据方差尽可能的大。假定训练集X={(x1,y1),(x2,y2),…,(xN,yN)}， 其中任一样本xi包含n维特征，yi∈{0,1}。 PCA作为特征映射算法，算法流程如下：

(1)对X进行中心化，得到Xc；

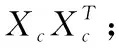
3.2 LDA用作特征映射

LDA是一种有监督的特征变换技术，能合理运用标签信息，使得投影后的维度具有判别性，不同类别的数据尽可能分开，同类别的数据尽可能靠近。采用LDA作为特征映射算法，将数据映射到具有可分性的特征空间，算法流程如下：

假定Xm(m=0,1) 为第m类样本的集合，而um(m=0,1) 为第m类样本的均值向量，定义∑m(m=0,1) 为第m类样本的协方差矩阵。

(1)计算每个类的类内散度矩阵之和Sw

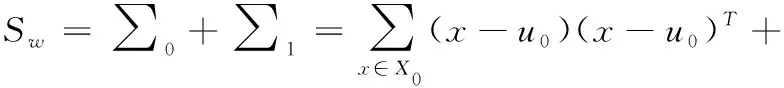
(5)

(2)计算类间散度矩阵Sb

Sb=(u0-u1)(u0-u1)T

(6)

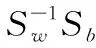
3.3 实例相关代价敏感组合旋转森林ECS_CROF

下面给出本文提出的实例相关代价敏感组合旋转森林ECS_CROF的构建步骤，图1展示了ECS_CROF算法框架。用F表示样本完整的特征集。T1,T2,…,TD表示使用D个基分类器。

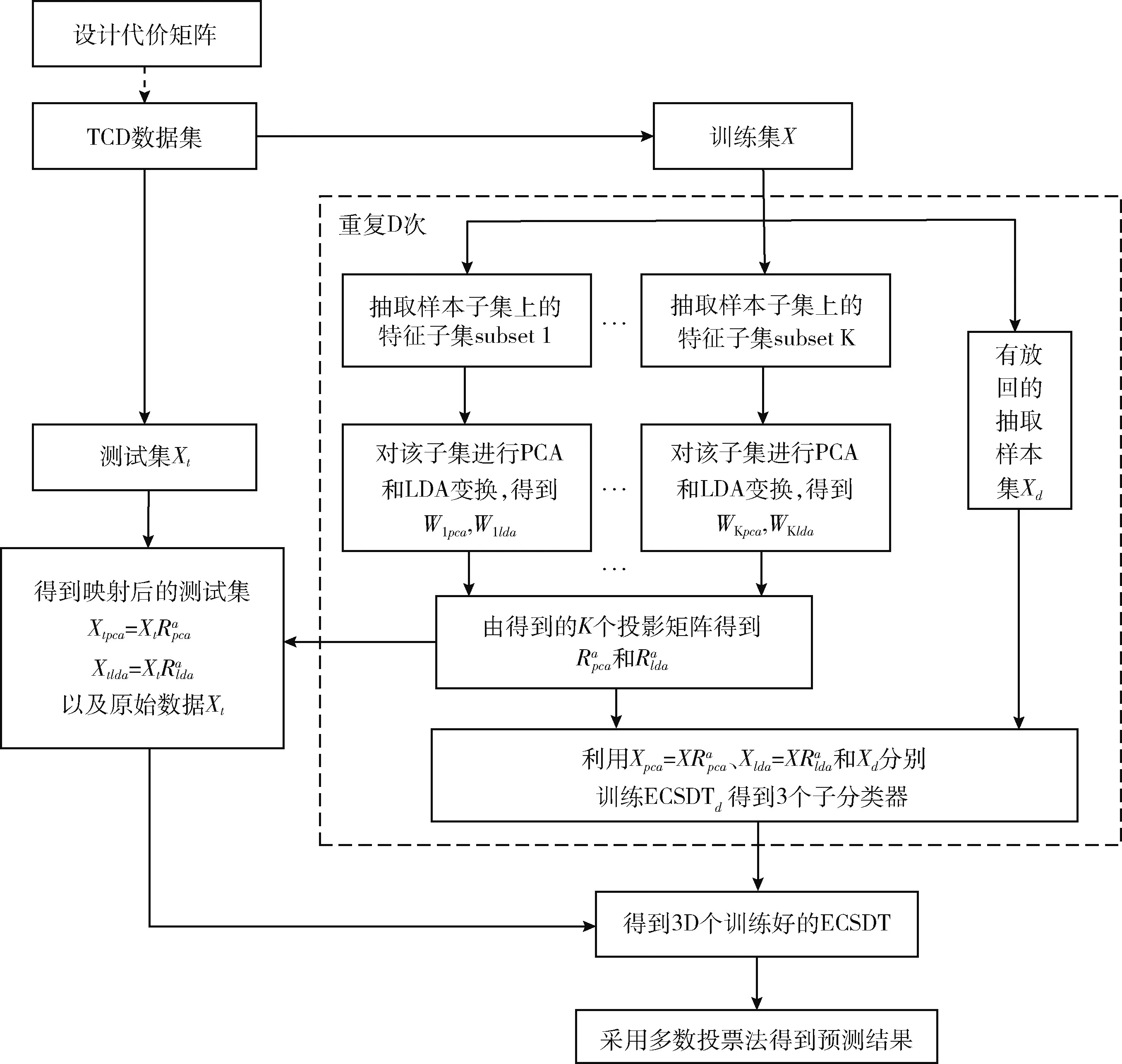
图1 实例相关代价敏感组合旋转森林框架

(1)针对训练集X，随机将F划分为K个不相交的特征子集，每个子集包含M=n/K个特征，若K不能整除n，最后一个子集将是n除以K的余数。令Fd,k(1≤d≤D,1≤k≤K) 为第d个基分类器的第k个特征子集，对训练样本集按一定比例进行重复抽样，得到新的训练样本子集X′，对此样本子集上的Fd,k特征子集进行PCA和LDA变换，得到投影矩阵Wkpca，Wklda。

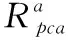
(7)

(4)将以上步骤重复D次，得到3D个训练好的ECSDT。

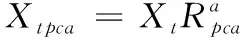
4 实 验

4.1 实验设计

本文根据山西省人民医院神经内科的TCD数据设计了两组实验，分别为“正常人-硬化患者”，“正常人-狭窄患者”，每组实验分别对“原始特征”和“融合特征”进行对比实验。将所提出的ECS_CROF与实例相关代价敏感随机补丁ECSRP[5]，基于PCA特征映射的实例相关代价敏感旋转森林(用ECSROF_PCA表示),以及基于LDA特征映射的实例相关代价敏感旋转森林(用ECSROF_LDA表示)进行比较，以此验证所提出的ECS_CROF算法的有效性。将数据进行五折交叉验证，每一折都划分为训练集、验证集和测试集，使用网格寻优算法对模型进行参数寻优，寻优的目标函数为“成本节约(Savings)”，取五折交叉验证的平均值评估算法的整体性能。

4.2 评价指标

传统的分类性能评价指标，如准确率(accuracy)、几何平均(geometricmean，Gm)、召回率(recall)等，只强调准确性而不考虑误分类所产生的代价。实例相关代价敏感问题需要评估的是算法在降低成本方面的性能，而不仅仅强调准确性。

本文使用Savings指标评价算法的成本节约性能[4]。首先，计算将所有实例分为负类或正类时(即代价最大时)所产生的总代价Costbase(X)，然后将成本节约Savings定义为在实际预测中使用算法预测结果所产生的代价Cost(f(X)) 相比于Costbase(X)所带来的成本节约量

(8)

其中，Costbase(X) 为Cost(f0(X)) 和Cost(f1(X)) 之间的最小值，fa(X)=a，a∈{0,1}。 Savings值越大，说明算法在节约成本方面的性能更优越。

本文还采用了传统的Gm、Recall和特异性(specificity，Sp)评价指标，Gm为Recall和Sp的几何平均，Recall表示在所有患者中，被正确识别出的患者比例，Sp表示在所有正常人中，被正确识别出的正常人比例，对应的公式如下所示

(9)

(10)

(11)

式中：FP(false positives)代表实际为负类样本，但被错误预测为正类样本的数量，FN(false negative)代表实际为正类样本，但被错误预测为负类样本的数量。TP(true positives)、TN(true negative)分别表示的是实际为正(负)类样本且被正确预测为正(负)类样本的数量。

4.3 实验结果与分析

(1)验证组合特征的有效性。表3给出了本文方法及对比方法用于分类脑卒中TCD数据的Savings实验结果，可以看出，采用融合特征后，对于硬化患者(实验①②)和狭窄患者(实验③④)，各个方法的Savings值都有一定的提升。由此可见，本文构建的组合特征有实际效用，能更好挖掘脑卒中TCD数据信息。

(2)验证本文算法ECS_CROF的有效性。由表3的实验结果可以看出，对于硬化患者和狭窄患者，本文的方法的Savings都是最优的，可见本文方法ECS_CROF用于不平衡TCD数据的成本节约性能最优。此外可以看出ECSROF_PCA和ECSROF_LDA的性能均优于ECSRP，由此验证了旋转森林模型的有效性。在实验①②③中ECSROF_LDA的性能均优于ECSROF_PCA，实验④中两者性能差别不大，ECSROF_LDA只是略低于ECSROF_PCA，说明利用LDA技术代替PCA进行特征投影，可以进一步提升旋转森林模型性能。

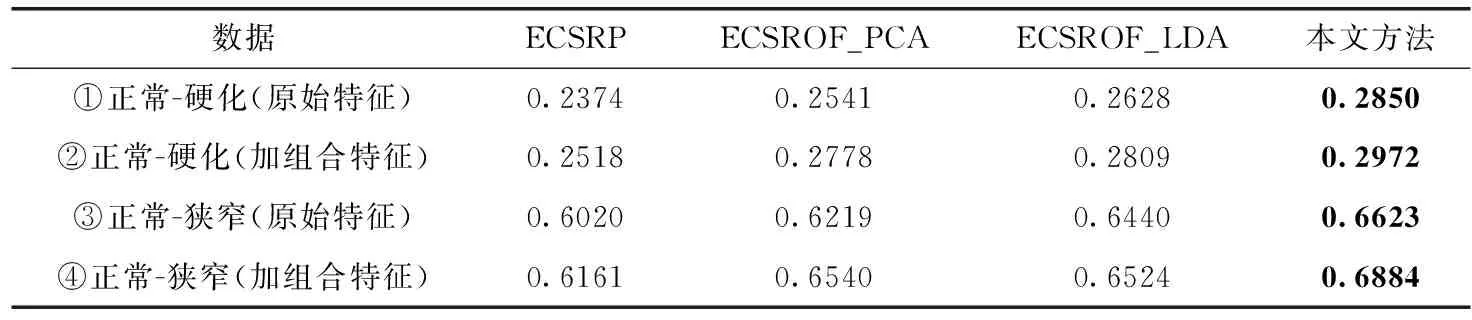
表3 不同算法对脑卒中TCD数据的Savings性能对比

(3)本文进一步对比分析了4种方法的传统评价指标Gm、Recall和Sp。对比结果见表4，可见本文方法ECS_CROF的Gm参数和Savings性能类似，仍然是最优的，进一步验证了本文方法的有效性。由表3和表4实验①可见，ECSRP的Savings指标不如ECSROF_PCA，但是Gm却优于后者；由实验④可见ECSROF_LDA的Savings指标不如ECSROF_PCA，但是Gm却优于后者；可见Gm指标和Savings并没有严格的正相关或负相关关系，因为Savings考虑了每个实例的代价，更具有实际参考价值。

此外相比于ECSROF_LDA和本文方法ECS_CROF，ECSROF_PCA的Recall更高但是其Savings和Gm性能都较差，这是因为ECSROF_PCA判别能力较差，受到代价矩阵的影响便一味提高Recall，却将大量的正常人误判为了患者，也就是Sp指标较差，最终导致Savings和Gm效果较差，这在现实生活中，势必会因为大量的复查造成极大的资源浪费，失去了代价敏感分类的意义。然而本文提出的方法ECS_CROF能够保证较高Recall的同时，很好提升Savings和Gm指标，说明本文方法通过综合不同的特征空间，更好权衡Recall和Sp两个指标，最终取得最优的成本节约性能Savings。

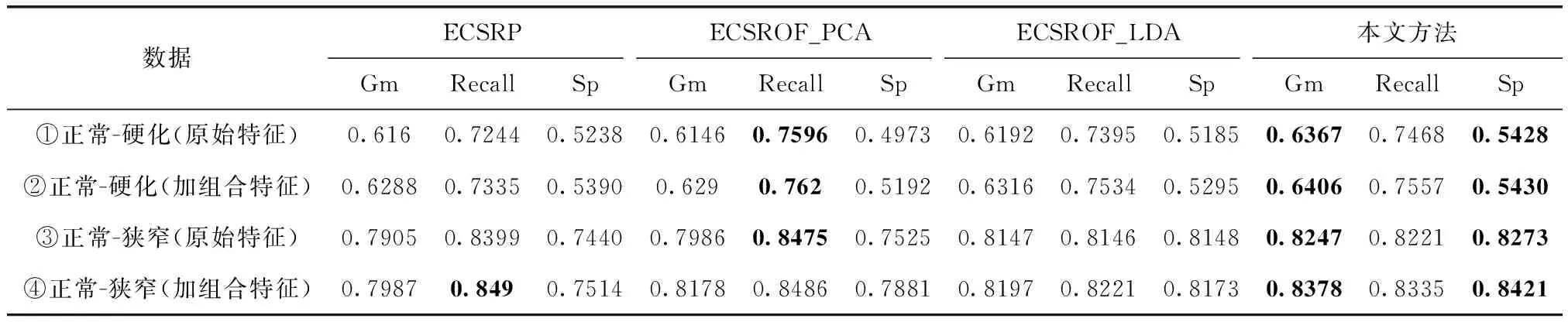
表4 不同算法对脑卒中TCD数据的Gm、Recall和Sp性能对比

总之，本文提出的组合特征能更好挖掘数据潜在信息，针对不同的算法，均能有效提升数据可分性；此外，本文提出的ECS_CROF的Savings和Gm指标均优于对比算法，可见本文提出的算法，能有效提升模型性能，更好节约成本，更具有实际的参考价值。

5 结束语

首先根据脑卒中TCD数据特点，本文构建了多个组合特征，充分挖掘数据的潜在信息来提高其分类性能。然后根据脑卒中的实例相关代价敏感特性，本文设计了适用于脑卒中的新的代价矩阵，用于实例相关代价敏感算法，并用“成本节约(Savings)”评估算法性能。最后提出了实例相关代价敏感组合旋转森林算法用于脑卒中TCD数据分类，结果显示，与已有的实例相关代价敏感算法相比，所提的ECS_CROF在成本节约上性能更为显著。本文仅对代价敏感脑卒中早期筛查诊断做出初步的探索，今后，可以综合考虑多方面因素，设计更加精细的脑卒中代价矩阵；采用其它的特征映射算法，构建更多样的旋转森林，进一步改善性能指标。