一种改进的KNN案例推理检索算法*
孙宝贵,车文刚,廖江福
(1.昆明理工大学信息工程与自动化学院,云南 昆明650500;2.昆明理工大学云南省计算机技术应用重点实验室,云南 昆明650500)
1 引言
案例推理CBR(Case-Based Reasoning)是人工智能领域中一种基于现有知识的问题求解与学习方法,其通过重用或修改与目标案例相似性高的历史案例解决问题[1]。目前,对CBR的应用与研究非常广泛[2 -5],应用最为广泛的CBR模型是Aamodt等[6]提出的“4R循环”,包括以下4个环节:(1)案例检索(Retrieve):从案例库中检索与目标案例相似性最高的一个或多个相似源案例;(2)案例重用(Reuse):将检索得到的相似源案例作为建议解;(3)案例修正(Revise):对建议解进行评估。若评估合格,则不需要修正;若评估不合格,则对建议解进行相应的修正;(4)案例保存(Retain):将目标案例及其解决方案作为新案例存储到案例库中。
案例检索是案例推理的中心环节,因此,检索算法的性能直接影响案例推理检索结果的精度和执行时间[7]。目前常用的案例推理检索算法有:知识引导法(Knowledge-Guided)、归纳索引法(Induce Indexing)和K-最近邻KNN(K-Nearest Neighbor)算法等。其中,由于K-最近邻算法通过欧氏距离实现相似性计算,所以被广泛应用于案例推理。
但是,传统的KNN算法在检索案例时存在2处缺陷:(1)计算量大,效率低。传统KNN算法需要对案例库中所有的案例进行相似度计算。因此,对于海量案例库而言,计算量巨大,会降低效率。(2)近邻K值影响最终的输出结果。当K值较小时,容易发生过拟合;当K值较大时,会将噪声点划分为相似源案例,导致输出结果的误差增大,质量下降[8]。
目前对于改善传统KNN算法性能、提高案例推理检索效率的研究颇多。张春晓等[9]提出了一种通过遗传算法、内省学习和群决策思想改进的CBR分类方法。但是,该方法需要多次迭代实验,才能确定最佳匹配属性与不匹配属性的阈值。严爱军等[10]提出了一种基于可信度阈值优化的CBR评价分类方法,以改善CBR分类器性能。然而其存在一个问题:可信度阈值优化方法能否划分出合理的可信集与不可信集。樊瑞宣等[11]提出了一种个性化K近邻的检索算法,其每个样本的近邻K值通过算法自动确定。但是,文献[11]算法需要对每个样本优化近邻K值,因此时间复杂度相对较高。万碧君等[12]提出了一种改进K最近邻回归建模算法。文献[12]中改进的算法虽然提高了检索效率,弥补了传统KNN算法的2个缺陷,但是其采用的K-Means和粒子群优化算法都存在易陷入局部最优解的问题,且粒子群优化算法不易收敛。
针对传统KNN检索算法的2处缺陷及其现有研究的不足,本文提出一种改进的KNN案例推理检索算法(SAGA-FCM-GAPSO-KNN_Opt_Stra):以遗传模拟退火-模糊C均值聚类SAGA-FCM(Simulated Annealing Genetic Algorithm-Fuzzy C-Means)算法对案例库聚类;利用改进的遗传-粒子群优化混合GA-PSO(Genetic Algorithm-Particle Swarm Optimization)算法优化各类簇的近邻K值;然后,提出最优原则的检索策略,确定目标案例的检索子案例库及近邻K值;最后,利用Mackey-Glass混沌时间序列数据验证改进的KNN案例推理检索算法的有效性。
2 相关内容
2.1 CBR问题描述
一般地,案例在案例库中采用二元组形式存储:
Ck={Xk;yk},k=1,2,3,…,n
其中,n为案例库Ck中的源案例总数,yk为第k条源案例的类型,Xk为第k条源案例的问题描述,可以表示为:
Xk={x1k,x2k,x3k,…,xik,…,xmk},
i=1,2,3,…,m
其中,m为案例的特征属性总数,xik为第k条源案例的第i个特征属性。
以线性问题类型的案例推理为例,Ck={x1k,x2k,x3k,…,xmk;yk} 。xmk与yk都是实数,且m个特征属性间接地决定输出值。
2.2 K最近邻回归算法
K最近邻算法KNN是1967年由Cover和Hart[13]提出的一种基本分类与回归算法,是最简单的机器学习算法之一。相较于其他常用的检索算法,KNN是基于距离的相似性度量算法,没有检索过程繁杂以及对数据的归纳整理操作。
一般地,在案例推理中应用KNN算法,有以下3个步骤:
步骤1计算目标案例与案例库中所有案例的距离-特征项距离和;
步骤2从案例库中选择K个距离最小的案例作为相似源案例;
步骤3利用K个相似源案例预测输出最终结果。
一般地,KNN算法采取求K个相似源案例的输出值的平均值或加权平均值作为预测结果:
平均值如式(1)所示:
(1)
加权平均值如式(2)所示:
(2)
其中,ωi为yi的权重。
3 改进的KNN案例推理检索算法
针对聚类与近邻K值问题,本文利用遗传模拟退火-模糊C均值聚类算法实现案例库聚类,通过改进的遗传-粒子群优化混合算法优化每个类簇的近邻K值。
3.1 基于遗传模拟退火-模糊C均值聚类算法的聚类
将聚类思想应用到案例推理的检索过程,有利于减少检索时间,提高检索质量。常用的聚类算法有:K-Means聚类算法、模糊C均值聚类算法、支持向量机算法、神经网络和遗传模糊C均值聚类算法等。
相较于K-Means聚类算法,模糊C均值聚类算法是一种基于目标函数的模糊聚类算法。其在K-Means聚类算法的基础上增加了隶属度函数,用来描述样本与某一类簇的相似程度,使得样本的隶属度可以为[0,1]的实数。基于此,假设一个数据集X有n个样本,聚类数为cn。其目标函数为:
(3)

隶属度函数uij如式(4)所示:
(4)
类簇中心cj如式(5)所示:
(5)
但是,模糊C均值聚类算法本质上依然是局部搜索优化算法。与K-Means算法一样,若初始值选择不当,就会收敛到局部最优解。
因此,本文采用遗传模拟退火-模糊C均值聚类SAGA-FCM算法实现案例库聚类。遗传模拟退火算法作为一种改进的优化算法[14],在优化算法前期,初始化生成的种群中个体的差异较大,即个体的适应度值相差较大,因此会存在部分较为优秀的个体,而此时模拟退火算法中的温度值较高,有较大的概率接受较劣个体成为新解,以避免整个种群较早地收敛于局部优秀个体,出现陷入局部最优解的问题;在优化算法后期,整个种群中个体的适应度值基本相同。此时温度值较低,模拟退火算法可以适当拉伸遗传算法中种群个体的适应度值,扩大种群个体间适应度值的差异,提升优秀个体在后期迭代过程中的优势,克服了遗传算法在种群后期进化时停滞不前的缺点。因此,遗传模拟退火算法可以提高全局与局部的搜索能力与效率,能够解决FCM算法或K-Means算法因初始值选择不当,导致算法陷入局部最优问题。所以,遗传模拟退火-模糊C均值聚类(SAGA-FCM)算法可以更加稳定有效地收敛到全局最优解,具体步骤如算法1所示。
算法1遗传模拟退火-模糊C均值聚类算法
输入:数据集X,类簇个数cn。
输出:cn个不同簇间疏散、同簇内密集的类簇。
步骤1初始化种群控制参数:种群规模pop_size,最大进化次数max_Iterate,交叉概率Pc,变异概率Pm,退火初始温度Tstart,冷却系数J,终止温度Tend。
步骤2随机初始化cn个类簇中心,并生成初始种群Chrom。对每个类簇中心用式(4)计算各样本的隶属度,以及用式(3)计算每个个体的适应度值Fi,其中i=1,2,…,pop_size。
步骤3设置进化迭代参数Iterate=0。
步骤4对种群Chrom进行选择、交叉和变异等遗传操作,对新产生的个体用式(4)和式(5)计算各样本的隶属度以及cn个类簇中心,并用式(3)计算每一个体的适应度值fi。若fi>Fi,则用新个体替换旧个体;否则,以概率P=exp((Fi-fi)Ti)接受新个体,抛弃旧个体,其中,Ti为模拟退火时,每次冷却的温度。
步骤5令Iterate=Iterate+1,若Iterate 步骤6令Ti=J*Ti-1,若Ti>Tend,则转至步骤3;否则,输出最优结果。 由此,得到cn个不同簇间疏散、同簇内密集的类簇。 一般地,使用交叉验证法或者优化算法确定近邻K值,比如遗传算法、粒子群优化算法和灰狼优化算法。但是,遗传算法容易出现早熟收敛的情况;粒子群优化算法与灰狼优化算法都存在局部最优解且不易收敛的缺点。因此,本文采用改进的遗传-粒子群优化混合GA-PSO算法,可以有效地避免局部最优以及早熟收敛的缺陷。具体算法步骤如算法2所示。 算法2遗传-粒子群优化混合算法 输入:cn个类簇。 输出:cn个类簇的近邻K值。 步骤1初始化粒子群并对其编码,本文采用真实值整数编码,如:02,12,36。 步骤2计算各类簇中每个案例与同类簇中其他案例的距离,并将距离值按升序排序。 步骤3通过适应度函数计算每个粒子的适应度值。其中,适应度值为当前粒子值下,预测输出值的均方误差值,如式(6)所示: (6) 其中,N为类簇内案例的个数;yj,real为第j个案例输出值的真实值;yj,pre为第j个案例输出值的预测值,如式(7)所示: (7) 其中,yi为升序排序后前K个案例输出值的真实值。d为当前粒子数,表示某案例在类簇中最相似的d个案例,即步骤2中升序排序后的前d个案例。 步骤4根据粒子适应度值更新粒子最优值Pbest和群体最优值Gbest。 步骤5将群体最优值Gbest十位上的数值对应交叉到粒子值的十位上,若新粒子的适应度值优于未交叉粒子的适应度值,则更新粒子及其适应度值。例如:群体最优值Gbest=16,当前粒子individual=32。交叉后的粒子new_individual=12。 步骤6对粒子上的个位值、十位值进行变异,若新粒子的适应度值优于未变异粒子的适应度值,则更新粒子及其适应度值。 步骤7循环执行步骤3~步骤5,直到满足结束迭代的条件。 步骤8输出cn个类簇的近邻K值。 本文采用平均值作为预测结果。因此,当聚类以及优化近邻K值的工作完成后,需要确定目标案例的检索子案例库及其近邻K值,才能开始检索案例并计算平均值。 一般地,确定目标案例的检索子案例库步骤如下所示: 步骤1通过式(8)计算目标案例与各类簇中心的距离distj: (8) 其中,m为案例中特征属性的个数;h′i为目标案例的第i个特征属性的值;vj,i为类簇j中心的第i个特征属性的值。 步骤2根据式(9)确定最小值距离Min: Min=min(dist1,dist2,…,distcn) (9) 其中,cn为类簇个数,distcn为第cn个类簇的类簇中心与目标案例的距离。 步骤3依据最小值Min找到相应的类簇,将该类簇作为目标案例的检索子案例库,并确定其近邻K值。 但是,上述方法可能存在一个现象:除却最小距离Min外,个别目标案例与剩余类簇中心的距离中还存在几乎等于最小距离Min的值。这说明存在此现象的目标案例恰好处于2个类簇的边界,且距离2个类簇中心的距离几乎相等。 因此,上述方法在确定此类型目标案例的检索案例库时,会强制剔除掉较相似的类簇,将其划分到最相似的类簇中。这会导致此类型目标案例损失部分相似历史案例,使其检索案例库减小。 针对上述现象,本文提出一种最优原则的检索策略。最优原则检索策略的具体步骤如下所示: 步骤1通过式(8)计算目标案例与各类簇中心的距离distj; 步骤2将各个距离distj按升序排列成(dist1,dist2,…,distcn),并通过式(10)计算Dist: Dist=dist2-dist1 (10) 步骤3通过判断Dist与阈值的大小,确定dist2对应的子类簇是否归并到目标案例的检索子案例库; 步骤4如果Dist大于阈值,目标案例的检索子案例库为dist1对应的子类簇,其近邻K值为该类簇的近邻K值; 步骤5如果Dist小于或等于阈值,目标案例的检索子案例库为dist1、dist2对应的子类簇,其近邻K值为2个类簇近邻K值的平均值。 根据上述步骤可得到各目标案例的检索案例库和近邻K值。 本文利用遗传模拟退火-模糊C均值聚类算法对案例库进行有效分类,然后通过改进的遗传-粒子群优化混合算法优化近邻K值,最后根据提出的最优原则检索策略,确定检索子案例库及其近邻K值,预测输出结果。具体的检索流程如图1所示。 Figure 1 Flow chart of the improved KNN retrieval algorithm of case-based reasoning proposed in this paper图1 本文改进的KNN案例推理检索算法的流程图 当φ=17时,上述微分方程呈现混沌特性。本文仿真取φ=30,通过Runge-Kutta方法生成20 000个数据。去掉前5 000个暂态点,从剩下的点中选取1 000个数据点。其中,前800个数据点组成训练集,后200个数据点组成测试集。对选取的数据点进行异构重组,得出时延为1,嵌入维为4[15],即一个案例由5个数据点组成,前4个数据点决定后1个数据点,如图2所示。 Figure 2 Heterogeneous reorganization of data sets to form case base图2 数据集异构重组形成案例库 本文进行了2组实验: 实验1不考虑目标案例的边界问题,即未采用最优原则检索策略,比较本文提出的检索算法与其他4种检索算法的预测结果,以验证本文提出的检索算法在未采用最优原则检索策略时具有良好的预测能力。 实验2考虑目标案例的边界问题,比较结合最优原则检索策略前后,本文提出的检索算法的预测结果,验证最优原则检索策略的有效性。 评价2组实验预测结果的指标采用均方误差值MSE(Mean Squared Error)和平均绝对百分误差MAPE(Mean Absolute Percentage Error)。 以下为本文采用的5种检索算法: (1)传统KNN检索算法(未采用最优原则检索策略),记为KNN; (2)基于模糊C均值聚类算法和粒子群优化算法改进的KNN检索算法(未采用最优原则检索策略),记为FCM-PSO-KNN; (3)基于遗传模拟退火-模糊C均值聚类算法和粒子群优化算法改进的KNN检索算法(未采用最优原则检索策略),记为SAGA-FCM-PSO-KNN; (4)基于灰狼-支持向量机算法和遗传-粒子群优化混合算法改进的KNN检索算法(未采用最优原则检索策略),记为GWOSVM-GAPSO-KNN; (5)基于遗传模拟退火-模糊C均值聚类算法和遗传-粒子群优化混合算法改进的KNN检索算法(未采用最优原则检索策略),记为SAGA-FCM-GAPSO-KNN; (6)本文提出的检索算法(采用最优原则检索策略),记为SAGA-FCM-GAPSO-KNN_Opt_Stra。 对于聚类及优化近邻K值的算法,有以下要求:模拟退火算法与粒子群优化算法要保证局部搜索能力,且收敛速度不宜太慢;遗传算法需保证全局寻优能力等。本文提到的算法的参数设置如表1所示。 Table 1 Parameter setting of each algorithm表1 各算法的参数设置 Figure 4 Partial figure of prediction results by 5 retrieval algorithms图4 5种检索算法预测结果的局部图 本文采用Davies-Bouldin指标DBI(Davies Bouldin Index)对聚类的最佳类簇数进行评价,其定义如式(11)所示: (11) (12) (13) 其中,xi表示类簇C中第i个样本的值,|C|表示类簇C中样本的个数;ci表示第i个类簇;avg(C)表示类簇C的类内样本的平均距离;u为类簇C的中心点。 DBI通过计算任意2类簇的类内平均距离之和除以2类簇中心距离,最后求最大值。DBI越小意味着类簇内距离越小,类簇间距离越大,聚类效果越好。 (1)不考虑目标案例边界问题,比较5种检索算法的预测结果。 通过Davies-Bouldin评价指标确定最佳仿真类簇个数为4。4种改进的KNN检索算法对训练集聚类,其结果为:158*5,170*5,200*5,266*5。相应的近邻K值为:11,14,10,19。传统KNN的近邻K值为训练集数目的平方根,即仿真数据取26。5种检索算法仿真结果如图3和图4所示。 Figure 3 Comparison of prediction results of 5 retrieval algorithms图3 5种检索算法的预测结果对比图 图3和图4能够具体展现各检索算法预测结果的拟合情况,其中 SAGA-FCM-GAPSO-KNN检索算法具有良好的拟合效果。拟合效果最差的是传统KNN检测算法,可以看出大部分案例的预测值与真实值有一定的差距。4种改进的检索算法中,GWOSVM-GAPSO-KNN算法预测结果波动性较大,拟合效果相对较差。 由表2可知,5种检索算法中,MSE、MAPE最小的是SAGA-FCM-GAPSO-KNN算法,其次是SAGA-FCM-PSO-KNN算法,最差的是传统的KNN算法。在改进的4种算法中,预测效果最差的为GWOSVM-GAPSO-KNN算法。通过比较FCM-PSO-KNN与SAGA-FCM-PSO-KNN以及GWOSVM-GAPSO-KNN与SAGA-FCM-GAPSO-KNN的MSE和MAPE发现:在优化近邻K值算法相同的情况下,SAGA-FCM聚类算法效果最好,说明SAGA算法可以有效地解决FCM算法易陷入局部最优的问题;比较SAGA-FCM-PSO-KNN与SAGA-FCM-GAPSO-KNN的MSE发现:在聚类算法相同的情况下,GAPSO算法优化近邻K值的效果最佳。因此,SAGA-FCM-GAPSO-KNN算法在检索案例时预测结果最好。 Table 2 Evaluation index of prediction results of 5 retrieval algorithms表2 5种检索算法预测结果的评价指标 从图4可看出,5种检索算法对案例6~案例12、案例50~案例55、案例106~案例110、案例127~案例131、案例184~案例190预测的结果皆存在明显的误差。通过分析数据发现:上述目标案例与4个类簇中心的距离中,次小距离值与最小距离值非常接近。因此可以验证这些目标案例存在边界问题。上述部分目标案例与4个类簇中心的距离,如表3所示。 由表3可知:上述目标案例与4个类簇中心的距离按照升序排序后,前2个最小距离的最小为0.003,最大为0.099,因此,本文提出的最优原则检索策略中的阈值取为0.1。下节实验考虑目标案例的边界问题,比较采用最优原则检索策略前后本文检索算法的预测结果。 Table 3 Distance between some target cases and the centers of 4 clusters(SAGA-FCM-GAPSO-KNN)表3 部分目标案例与4个类簇中心的距离(SAGA-FCM-GAPSO-KNN算法) (2)比较SAGA-FCM-GAPSO-KNN与SAGA-FCM-GAPSO-KNN_Opt_Stra的预测结果。 通过上文的对比实验可知:不考虑目标案例边界问题的情况下,相较于其他检索算法,SAGA-FCM-GAPSO-KNN算法预测结果精度最高。基于此,本节实验将在SAGA-FCM-GAPSO-KNN算法基础上,采用最优原则检索策略,比较SAGA-FCM-GAPSO-KNN与SAGA-FCM-GAPSO-KNN_Opt_Stra的预测结果。采用最优原则检索策略后,上述目标案例的预测结果如表4所示。 由表4可知,相较于SAGA-FCM-GAPSO-KNN,采用最优原则策略后,SAGA-FCM-GAPSO-KNN_Opt_Stra算法有效解决了目标案例的边界问题,使目标案例的检索子案例库扩大,预测结果更接近真实值。虽然存在极个别预测结果不是最佳的情况(案例108、案例109、案例188),但相较其他算法,SAGA-FCM-GAPSO-KNN_Opt_Stra整体预测效果最佳。 SAGA-FCM-GAPSO-KNN与SAGA-FCM-GAPSO-KNN_Opt_Stra算法对上述目标案例预测的结果如图5所示,对整体目标案例预测的结果如图6所示。 从图5可直观看出,采用最优原则检索策略后,SAGA-FCM-GAPSO-KNN_Opt_Stra算法对200个目标案例进行预测时,显著地减小了因目标案例的边界问题而导致的误差,验证了本文提出的最优原则检索策略的有效性,改善了预测结果和整体的拟合效果。如图6所示。 Table 4 Prediction results of some target cases by each algorithm 表4 各算法对部分目标案例的预测结果 Figure 5 Partial figure of prediction results by the retrieval algorithm proposed in this paper图5 本文检索算法预测结果的局部图 Figure 6 Prediction results of the retrieval algorithm proposed in this paper图6 本文检索算法的预测结果 由表5可得,相较于KNN算法,SAGA-FCM-GAPSO-KNN_Opt_Stra算法对200个目标案例仿真预测结果的MSE、MAPE值分别提高了62.7%和44.7%。相较于SAGA-FCM-GAPSO-KNN算法,SAGA-FCM-GAPSO-KNN_Opt_Stra算法预测结果的MSE、MAPE值分别提高了18.9%和8.9%。因此,SAGA-FCM-GAPSO-KNN_Opt_Stra算法可以提高线性问题预测结果的质量。 Table 5 Evaluation index of the prediction result of each retrieval algorithm 表5 各检索算法预测结果的评价指标 案例推理的中心环节是案例检索。对于海量案例库,在处理线性问题时,传统的KNN检索算法需要对所有案例进行相似度计算,且固定近邻K值会影响预测结果的质量。因此,本文利用聚类、优化近邻K值思想和最优原则检索策略,提出一种改进的KNN案例推理检索算法。并通过Mackey-Glass混沌时间序列数据进行仿真,实验结果表明,针对线性问题,本文提出的改进KNN案例推理检索算法不仅解决了传统KNN检索算法存在的两大缺陷,而且还具有良好的预测能力,可以进一步改善预测结果。3.2 改进的遗传-粒子群优化混合算法优化近邻K值
3.3 最优原则检索策略
3.4 算法流程

4 实验及结果分析
4.1 实验方案


4.2 参数设置


4.3 聚类有效性评价指标
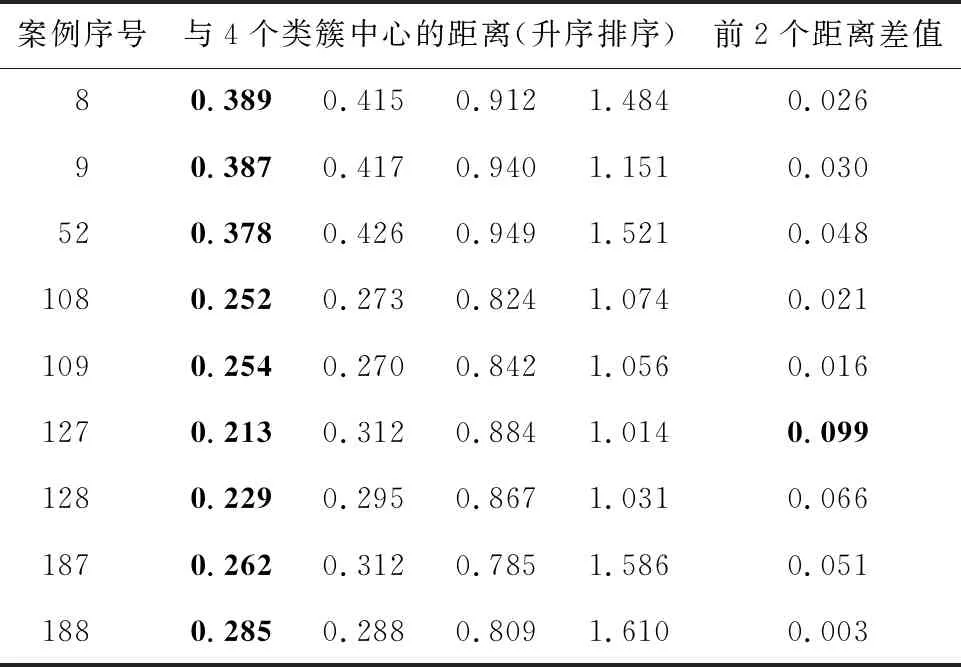
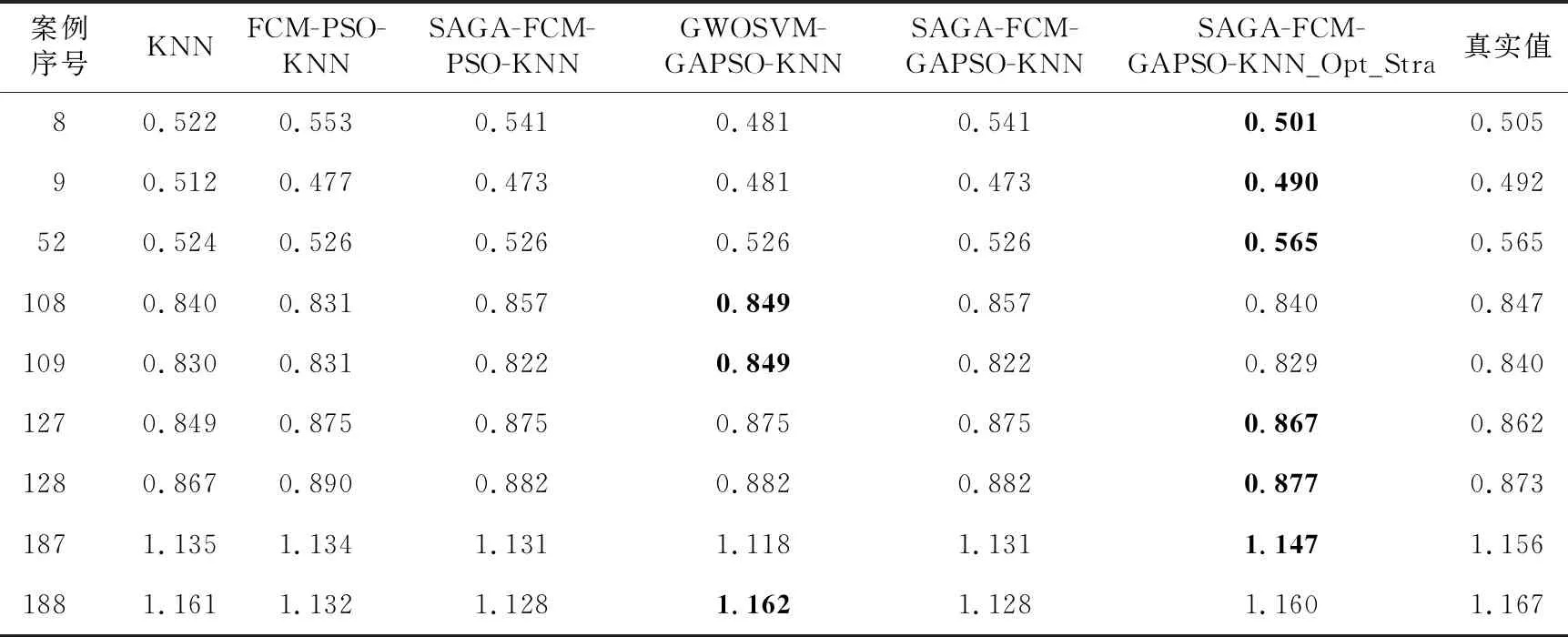
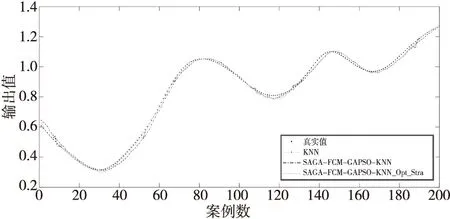
4.4 实验结果及分析




5 结束语

