基于变分模态分解和神经网络算法的微机械陀螺温度补偿

郭文静，曹慧亮

(1.太原工业学院 电子工程系，山西 太原 030008；2.中北大学 仪器与电子学院，山西 太原 030051)

0 引 言

微机械(MEMS)陀螺仪是重要的姿态检测器件，它基于哥氏力原理敏感角速度，是一种角速度测量的微型传感器，具备尺寸、功耗、精度、集成、稳定等多方面的独特优点，特别是体积小、高性能、高稳定性，使得其在自动控制、无人驾驶、航空航天、可穿戴设备、工业控制系统、消费电子等各领域有重要的地位和广泛的应用[1].但目前，温度特性是限制MEMS陀螺仪应用的主要因素之一，原因主要有硅结构封装方法会带有热应力，温度的改变极大地影响硅结构的主要物理特性，从而导致陀螺的性能不稳定，同时温度变化也会给陀螺的处理电路带来影响，所以许多研究者都很重视这一因素，在MEMS陀螺的温度误差处理方面做出了许多有效的工作[2].对于陀螺仪的温度补偿方法，主要有对陀螺内部的温度进行控制、器件的优化提升设计和陀螺温度输出算法处理补偿这3个方面，都取得了很好的效果[3].

DZ.Xia等人[4]提出了一种有效的控制系统对环境的温度进行控制，其中采用温度传感器实时检测温度，有很好的实验结果；S.H.Lee等人[5]采用了一种真空封装技术，使用该技术后能够很好地实现温度补偿，MEMS器件的温度系数大大降低，从17.3×10-6℃降到0.22×10-6℃；Yang等人[6]通过MEMS陀螺片上温度传感器对陀螺进行温度补偿，使内部芯片工作受温度变化的影响大大减小.温度控制方法直接对环境温度进行补偿，将温度控制在一个规定范围内，直接改善了器件的工作环境，该方法直观有效，但缺点是设计的系统复杂、实施困难，存在较大的功耗和可控温度范围有限等问题，造成了补偿效果的局限.

Cao和Li等人[7]研究了温度因素对陀螺结构力学模型的影响，并应用了一种有效的方法来提高硅结构的温度稳定性；Fu等人[8]通过配置电路，提出了一种简单且更合适的补偿方法，以减少谐振频率和阻尼系数的影响；在Zhang等人[9]的研究中，柱形陀螺仪采用热应力结构，提高了温度性能，结构优化后开环温度漂移率大大降低，降低了约2/3.Cao等[10]研究了硅结构陀螺仪在高温下的性能，提出了一种合理的硅结构等效电模型来提高精度，以应对由于温度过高而导致的性能不准确的难题.通过对陀螺进行硬件上的改善从而提升其对温度的敏感特性，从本质上对其进行温度特性的补偿，应用效果好，具有实时性，对长期漂移的抑制效果好.但同样存在不足之处，比如面对已经成型的器件难以使用，加工设计的成本耗费巨大且难度大，价格昂贵实现较为困难.

Zhang等人[11]通过全文范围的温度实验和数据处理，采用多项式拟合法建立了一种实用而精准的模型来补偿温度变化引起的误差，该方法实用且灵活，实验结果显示零偏为0.2 mV，证明了其有效性；Shen等人[12]采用基于EMD-ELM的多维并行方法处理双质量MEMS陀螺仪的温度误差，多维处理方法计算效率高，ELM预测运行速度快，实验的效果很好；I.P.Prikhodko等人[13]提出了一种MEMS陀螺长期漂移补偿方法，是一种实时温度漂移自补偿方法，驱动模态谐振频率作为内在温度检测装置，利用其线性频率温度依赖性，通过多项式拟合实现；许鹏等人[14]通过采用分段插值法提升陀螺的温度特性指标，在 -40℃～60℃范围内零偏稳定性提升了约 50倍.软件补偿方法具有高精度、高适应性等特点，更重要的是其成本低且可行性高，易于实现，对样本数据有一定的要求，先提取温度误差数据后对其中的映射关系进行建模即可获得补偿模型，因此应用广泛，随着算法的发展和硬件计算能力的提升，软件自补偿方法的发展也越来越快.

本文对MEMS陀螺的温度性能和补偿方法进行研究，采用软件补偿方法改善陀螺零偏等指标，提出基于变分模态分解和神经网络算法的温度漂移补偿技术，包含了高频噪声的消除与低频漂移的补偿，同时采用粒子群优化改进平行处理算法中存在的不足，提升模型自适应性和精度，构建内在温度特征映射关系，在温度变化环境中有效降低温度误差，具有较高的理论意义和实用价值.

1 MEMS陀螺基本理论

MEMS陀螺的工作原理是旋转的轴对称壳体激发弹性驻波的科里奥利效应，是一种哥氏振动陀螺仪，其工作机理是哥氏力耦合能量在驱动模态与检测模态之间的相互转移.通过对轴对称壳体敏感结构施加频率与陀螺敏感结构二阶固有频率相同的驱动力，使轴对称敏感结构进行稳定的弹性驻波4波幅运动，由于陀螺器件敏感到的惯性角速度与轴对称敏感结构的驻波进动量成正比，通过检测提取驻波进动量之后，即可检测陀螺仪的角速度.MEMS振动陀螺具有许多显著的优势，例如高精度、低能耗、长寿命和批量生产.

图 1 MEMS陀螺仪模型示意图

x轴为驱动振动方向，y轴为检测振动方向，z轴为外部角速度输入方向.当不考虑模态间耦合时，振动陀螺仪的动力学方程为

(1)

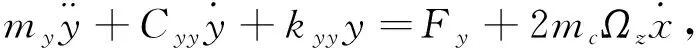
(2)

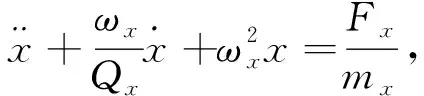
(3)

(4)

振动响应具有稳态和暂态分量，且暂态振动幅度随时间呈指数衰减，稳态响应为

x(t)=Axcos(ωdt+φd),

(5)

检测振动位移也由稳态和暂态分量组成，稳态响应为

y(t)=Aysin(ωdt+φd+φy),

(6)

图 2 MEMS陀螺仪开环检测框图

2 模型整体方案设计

在变化的温度环境中，陀螺输出含温度漂移，漂移趋势和温度为非线性关系，同时输出中白噪声幅度和频率也会随温度变化.针对这一特性，本文提出了基于变分模态分解(VMD)和反向传播(BP)神经网络算法的平行处理模型，算法流程如图 3 所示，具体步骤如下：

1) 进行MEMS陀螺仪的温度实验，获取在温度变化环境中的输出信号.采用粒子群优化的变分模态分解(PSO-VMD)，首先得到搜索优化的VMD内置参数，然后将陀螺输出的多分量复杂信号分解为预设尺度的调幅调频信号分量，即固有模态函数，不同模态函数代表了陀螺信号中的不同信号特征.

2) 采用样本熵(SE)对分解得到的固有模态函数(IMF)进行分析，将IMFs根据熵值大小分为噪声项、混合项和温度特征项.直接去除处于高频段的IMF(噪声项)，即去除纯噪声分量；对中间频率段的IMF(混合项)采用TFPF滤波，以保留其中的温度特征成分；之后与低频段的IMF(特征项)进行重建，即得到去除噪声后的陀螺输出信号.

3) 将温度序列进行处理，根据不同温度下持续的时间处理得到温度时间积分项，表征的是陀螺仪在某个恒定温度下的运行时间情况，由此构成一个二维度的温度序列，作为输入数据.利用二维温度输入和对应的漂移特征输出项对PSO-BP神经网络进行训练，得到PSO-BP神经网络模型.之后，将温度数据代入模型对陀螺零位进行补偿.之后进行信号处理重构，完成温度补偿.

图 3 MEMS陀螺温度补偿模型

3 陀螺仪温度实验

微机械陀螺受温度影响较为严重，通过进行温度实验来获取陀螺在不同温度环境下的输出信号.温度实验中使用的设备主要是高低温温控箱、数据采集卡、信号发生器和样品MEMS陀螺仪.实验设备如图 4 所示.实验室的温控箱可以精准控制温度，在-40℃～60℃温度范围内进行陀螺温度实验.操作装置旁的计算机用于收集微机械陀螺仪的输出信号.

图 4 温度实验设备

陀螺实验测试连接如图 4(c)，本次实验采用的是一个新型的双U型振动梁陀螺.首先，将样品陀螺放入温控箱中，降低温度至-40℃并保持1 h，保证陀螺在此温度下稳定运行后，将温控箱的温度变化范围设置为-40℃～60℃，温度每上升20℃后保持约1.5 h，以保证陀螺内部温度变化稳定，期间数据的采集是连续的，数据采集卡同时采集温度数据与陀螺输出数据，采样间隔设置为1 s，采样精度5.5 b，陀螺仪的输出和相对应的温度数据同时获取.

连续收集温控箱内温度和陀螺仪输出值的数据.为了避免偶然性，进行5组温度实验，结果数据大体一致，选取其中一组作为样本数据进行分析处理.实验采集陀螺仪的输出是温度与零偏的关系，图5是MEMS陀螺仪在温度实验中的输出曲线.

图 5 MEMS陀螺仪温度实验输出

通过图 5，可以看出微机械陀螺仪的输出信号具有如下特征：

1) 输出不是一个平稳的趋势，在整个温度测试中产生了较大的非线性不规则偏移，这说明输出信号受温度变化的影响很大.

2) 整个输出信号不平滑，比较粗糙，噪声来源多且其随着温度的变化也在发生变化，对真实结果会产生很大的干扰.

3) 在外部温度稳定在一个数值时，陀螺仪也存在明显的温度漂移.即使在同一个温度条件下，陀螺仪的输出也在不断变化，且该变化不具有规则性.

因此，对MEMS陀螺的温度误差补偿是十分有必要的.

4 算法处理与分析

4.1 信号降噪

温度实验的结果如图5所示，从图5中可以看出，温度从-40℃变化到60℃，MEMS陀螺仪的输出变化非常大，也就是说，温度变化极大地影响了MEMS陀螺仪的性能.因此，对陀螺仪的信号进行温度误差处理是有必要的.

温度的变化会导致MEMS陀螺的输出呈非线性不规则的变化，并且信号中含有大量的噪声，影响真实结果.噪声的来源很多，也会随着温度改变而发生变化.

本文所提出的温度误差处理模型，是并行处理.首先，采用PSO-VMD对输出信号进行分解，PSO搜索结果如图 6 所示，图 6 中圆圈代表粒子，灰色圆圈代表全局最优的粒子，由PSO搜索得到的α和K结果为[76 430,12]；然后，采用优化内置参数的VMD进行分解，如图 7 所示，VMD将MEMS陀螺仪输出信号按照频率有效分解为12个本征模态函数(IMF1-IMF12)，每个IMF自适应匹配一个固定带宽和中心频率.

(a) 1次迭代

图 7 PSO-VMD分解图

陀螺的输出信号由低频漂移和高频噪声组成，VMD分解提取了低频漂移和高频噪声，得到12个固有模态函数(IMF1-IMF12)，它们代表陀螺输出信号中的温度漂移特征和噪声信息.如果对每一个IMF进行处理，则计算消耗巨大且容易破坏静态信息，导致误差，因此这样本熵(SE)用于对模态函数进行分类，根据序列自相关性和复杂程度将IMF分为纯噪声项、混合项和温度特征项，如图 8 所示.

图 8 SE-VMD-TFPF降噪过程

如果IMF的样本熵值大于0.5，则它是不包含任何有用信号的纯噪声项，可直接将其删除；如果IMF的样本熵值在0.2～0.5之间，则为混合项，同时包含了有效温度特征和噪声，采用TFPF滤波，混合项的处理是温度补偿的重要部分，这里将TFPF算法设置为短窗滤波，在抑制噪声的同时保护静态特性，降噪结果在图 8 中显示.

若信号样本熵值小于0.2，则该信号是与温度相关的清晰的变化趋势，和经过时频峰值滤波后的混合项进行叠加，得到MEMS陀螺仪输出信号的去降结果，如图 9 所示.将原始信号和降噪信号进行比较，可以看出，降噪效果非常明显，很好地保留了温度漂移信息，从而证明了VMD-SE-TFPF平行降噪方法的有效性.

图 9 SE-VMD-TFPF降噪结果

4.2 温度漂移补偿

将二维温度序列和温度特征项作为补偿模型的训练集，训练神经网络，得到MEMS陀螺仪温度-漂移的输入输出映射关系.

首先需要对采集的温度数据进行处理，根据温度实验中陀螺温度与输出的关系可以得出：受温度变化的影响，输出也在随之改变，但它们不是一一对应的关系，即使温度恒定在某一个值不变，但输出在不断变化，而且，在不同的温度下，这种变化趋势也不同.换句话说，陀螺在一个温度下持续运行，输出会改变，且在不同温度下的变化趋势不同.这样的温度-输出是一个高度非线性的不规则关系，给温度补偿带来了很大的困难.单独的温度维度无法映射到输出，加上温度变化率构成的二维输入也无法完成映射，因为温度不变时温度变化率始终为零，特征无效.

本文引入温度的时间积分项，每当陀螺处于一个新的温度下运行稳定后开始进行时间的积分，描述的是陀螺仪在某个恒定温度下的运行时间情况，由此构成一个二输入单输出的映射关系，来提升补偿预测的精度.

在确定了训练集之后，训练PSO-BP神经网络模型，将网络设置为2-15-4-1结构，即总共4层网络，第1层(输入)含2个神经元；第2层(隐层)含15个神经元；第3层(隐层)含4个神经元；第4层(输出)含1个神经元.然后，编码粒子，问题的总维数为114，第1层到第2层连接权值有30个，即将其与粒子前30个维度对应；第2层含有阈值15个，与维度31到45对应，依次每个粒子包含的信息和网络结构参数一一对应.

PSO迭代过程适应度值变化如图 10 所示，可以看出粒子群全局搜索能力非常强，收敛速度快.

图10 PSO适应度变化曲线

经过粒子群30次更新计算，用解空间范围内最优结果更新网络参数，之后利用BP算法优秀的局部逼近能力进行训练，防止局部过拟合模型泛化能力差现象的发生，BP算法训练过程如图 11 所示，迭代31次后模型收敛.

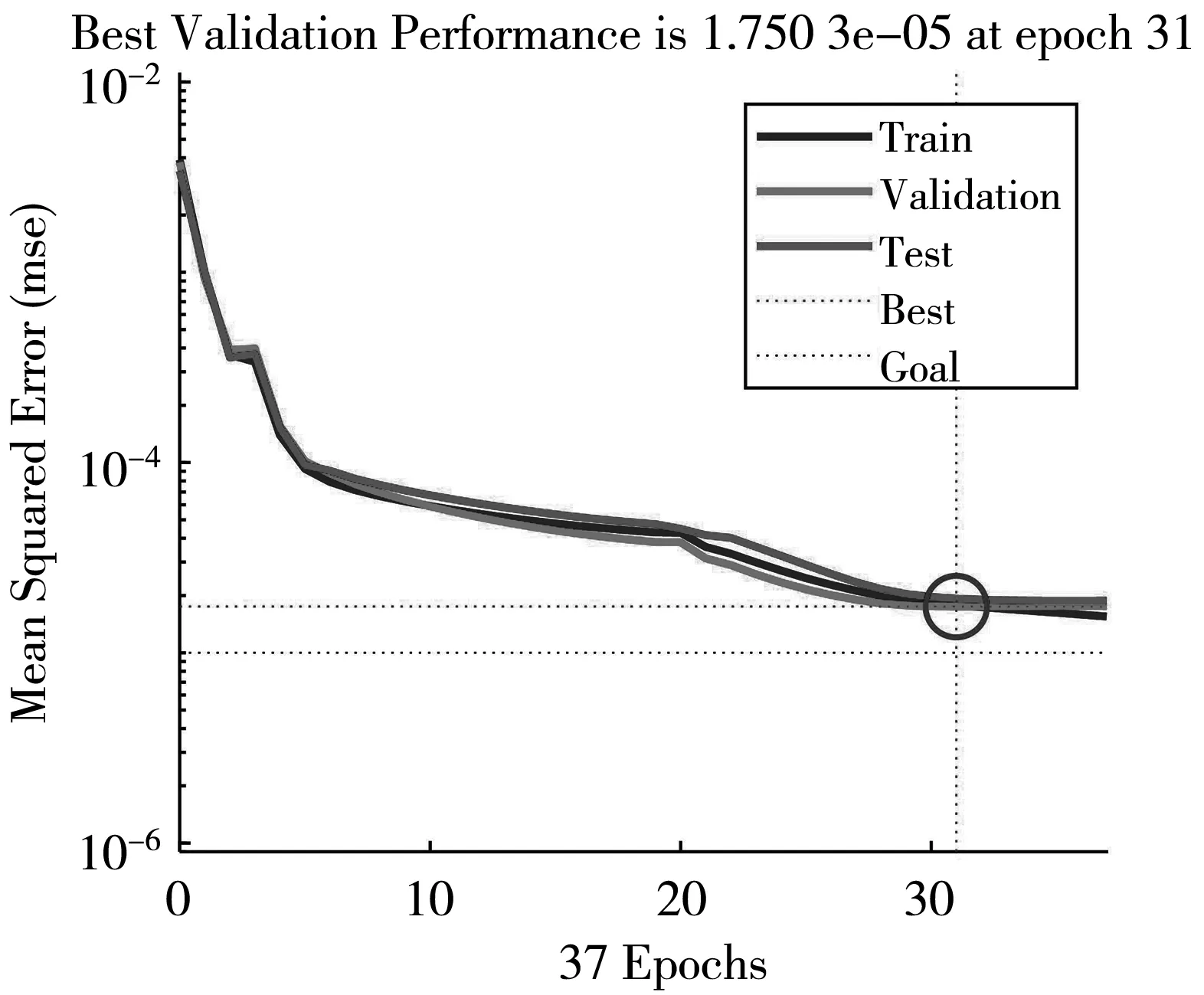
图11 神经网络模型收敛曲线

图 12 为PSO-BP神经网络模型回归结果.在混合项经过时频峰值滤波，温度特征项经过PSO-BP模型补偿后，重建信号并对序列进行平滑处理，去除由于温度突变产生的尖峰(构造的温度积分维度会在温度突变时产生尖峰)，之后获得最终的补偿结果，如图 13 所示，将温度补偿结果与原始的陀螺输出信号对比，可以看温度补偿具有很好的效果.

图 12 PSO-BP神经网络模型回归结果

图 13 原始输出与温度补偿信号

4.3 结果分析

本文采用Allan方差去分析所提出算法的性能.Allan方差是一个IEEE认可的标准的陀螺仪性能分析方法，被广泛应用[15].

图 14 Allan方差分析图

5 结 论

本文研究了MEMS陀螺仪的温度误差处理技术，基于变分模态分解和BP神经网络算法，包含了陀螺信号的去噪和温度补偿.该方法是一种多维度平行处理算法，主要应用了模态提取技术、时频降噪方法、机器学习以及粒子智能寻优方法.首先，用VMD分解对信号分层，提取特征，平行降噪模型能够有效去噪并且为网络预测训练提供精确的漂移目标.根据本征模态函数的自相关性，SE将IMFs分为纯噪声项、混合项和漂移项，极大地减少了计算消耗.混合项用时频峰值滤波，漂移项用神经网络补偿.同时采用PSO对算法的关键部分进行优化，针对变分模态分解算法中的分解层数和惩罚因子以及BP神经网络的初始连接权值和阈值进行优化处理，提高VMD算法的自适应能力，同时，解决BP神经网络可能会出现的过拟合、陷入局部优化等现象，提升温度补偿精度和模型鲁棒性.温度实验和Allan方差指标证明了该算法模型的有效性.