Interaction of Irregular Waves with Vertical Breakwater and Characteristics of Secondary Wave Generated by Overtopping

HAN Xinyu, JIANG Yunpeng, and DONG Sheng, *

Interaction of Irregular Waves with Vertical Breakwater and Characteristics of Secondary Wave Generated by Overtopping

HAN Xinyu1), JIANG Yunpeng2), *, and DONG Sheng1), *

1) College of Engineering, Ocean University of China, Qingdao 266100, China 2) Tianjin Research Institute for Water Transport Engineering, Tianjin 300456, China

This study investigated the interaction between irregular waves and vertical breakwater. The main goal was to determine the wave force on the breakwater for different depths, along with the evolution of the secondary wave generated by overtopping. The open source code DualSPHysics was used in the simulation. Wavelet transform was employed to remove the acoustic components from the weakly compressible smoothed particle hydrodynamics pressure solution. The results of the experiments and simulations showed that although the wave height at the low water level (case 2) was smaller than that at the high water level (case 1), the horizontal and uplifting force of case 2 was higher than that of case 1. In case 2, a large impact pressure occurred because of the plunging wave and wave breaking effects. As the water level was close to the breakwater top in case 1, the secondary wave generated by overtopping was studied. Results indicated that wave and breakwater interactions transfer wave energy from the leading wave component to higher harmonics. Two main harmonics were identified in the secondary wave. The first harmonic was the incident peak frequency, which was still the dominant component. During the wave propagation behind the breakwater, the frequencies of harmonics remained unchanged, but the amplitude of the first harmonic showed an obvious change. Under the same wave condition, the first and second harmonics did not change with depth.

irregular waves; vertical breakwater; wavelet; wave force; secondary wave

1 Introduction

A breakwater is an offshore structure that defends a- gainst waves and protects the stability of the ships within a harbor. With marine engineering developments in recent years, the water depth requirements of ports have increased. Thus, breakwaters have been placed increasingly farther from the coast. Therefore, wave breaking behavior and the wave load characteristics of the wave force at different depths should be comprehensively investigated, along with the effects of the secondary waves generated behind a dike in a harbor.

Minikin (1963) proposed a method for estimating the local pressure of a wave impacting a vertical breakwater or seawall. However, many studies have indicated that Minikin’s formula is incorrect because the impacting force decreases with an increase in incident wave length. Goda (1974) introduced a new formula for the wave load on a vertical wall on the basis of a series of experiments and theories. Then, further studies were conducted by Takaha-shi(1993, 1994). They considered the influences of berm, top slopping, wave breaking, and incident wave angle and developed Goda’s original formula. Goda (2000)developed a physically rational method for wave force assessment.

Using the physical model test from the probabilistic design tools for vertical breakwaters (PROVERBS), Kortenhaus(1994) and Klammer(1996) analyzed the horizontal wave impact force and uplifting load, respectively. Allsop(1996) and Allsop and Vicinanza (1996) developed a new formula for predicting the wave impact force on a vertical wall on the basis of experiments. As the research progressed, a new approach to the evaluation of the impact load on a vertical seawall or breakwater was proposed on the basis of PROVERBS (Allsop, 1999). This new method first considers the uncertainties and variability of the loading process. Therefore, it represents a step forward toward the development of increasingly rational and reliable design tools.

In the process of wave impact on a vertical wall, the entrapped air pocket exerts an important effect on the force exerted on the vertical wall. Bagnold (1939) emphasized the importance of entrained and entrapped air and observed that the greatest pressure occurs when the amount of air in the water is least but not zero. Obhrai(2004) found that the magnitude of peak pressure decreases with the amount of entrapped air and that pressure rise time increases. In addition, when a wave impacts a wall, the air pocket may generate pressure oscillations. Chan and Melville (1988) and Hattori(1994) found that in addition to its effect on pressure maxima, a trapped air pocket interacts with the surrounding fluid in a pulsating motion.

These studies mainly focused on proposing effective methods and formulas to provide a preliminary evaluation of the maximum wave force on a vertical seawall or break- water in practical engineering. However, none of them considered the history behind the wave-breakwater interaction. Thus, methods such as computational fluid dynamics (CFD) are necessary to analyze such interaction.

With the development of computer technology, calculations can be performed at increasingly rapid speeds. The use of numerical schemes to solve the governing equations of fluid mechanics has become popular. Describing flow motion, free surface deformation, and fluid-structure interaction is a complex problem in CFD. The nonlinearity of fluid motion is mainly manifested by capturing violent free surface deformations, such as those from wave impact, wave breaking, air pocket generation, and overtopping. The Lagrangian method and Eulerian method are the most commonly used numerical schemes for approximating the free surface in the flow process.

Traditional CFD methods, such as the marker and cell (MAC), volume of fluid (VOF), level set (LS), and constrained interpolation profile (CIP) methods, have been used to determine the fluid-structure interaction.

Harlow and Welch (1965) introduced the MAC method to simulate free surfaces. The MAC method was developed using the particle-in-cell technique, in which particles cover the whole fluid domain and move with the flow. The weakness of the MAC method is its expensive storage requirement.

Hirt and Nichols (1981) proposed the VOF method to capture free surfaces. Fluid fraction functionwas defined to represent the fluid volume state in a grid; anvalue of 0 or 1 indicated that the cell was filled with air or water, respectively. An F value between 0 and 1 indicated that the grid contained a combination of air and water,, a free surface. The VOF method is a simple and efficient method for capturing free surfaces and is widely used in coastal and ocean engineering (Higuera, 2013; Tsai, 2016; Sogut and Yalciner, 2019).

Osher and Sethian (1988) introduced the LS method to track fluid boundaries, and the technique has become popular in recent years because it can sharply model interfaces. However, the traditional LS method cannot guarantee mass conservation during the reinitialization process (Tornberg and Enhquist, 2000). In recent decades, many researchers have exerted effort to improve the method. Sussman and Puckett (2000) proposed the coupled level set/VOF method, which combines the advantages of the simple curvature calculation in the LS method and the mass conservation maintenance in the VOF method. Enrigh(2002) adopted a Lagrangian form for capturing interfaces so as to improve the mass conservation of the LS method.

The CIP method is a new method for capturing nonlinear free surfaces. The CIP scheme is a semi-Lagrangian numerical solver for hyperbolic equations (Takewaki,1985). This method explicitly transports a physical quantity and its spatial derivatives and interpolates them over a cell by third-order polynomials along the characteristic curve of a hyperbolic equation (Yabe and Wang, 1991). The CIP method is made advantageous by its compact high-order property and elimination of time step restrictions. However, the CIP method is not effective at mass conservation. Much work has been conducted to guarantee mass conservation. The CIP-conservative semi-Lagrangian scheme (CIPCLS) was proposed by Tanaka(2000), Nakamura(2001), and Yabe(2001). In the CIPCLS, an integrated form of variables is applied to the CIP scheme, and the advection and non-advection terms are treated separately. Mass conservation is maintained in each grid. Xiao(2005) presented the tangent of hyperbola for interface capturing (THINC) scheme to describe the interfaces in a multiphase flow with good mass conservation. Hu and Kashiwagi (2009) used the THINC scheme and virtual particle method to improve the non-conservation of the CIP scheme on the basis of a regular Cartesian grid.

The aforementioned methods were based on Euler mesh. They were not able to solve the free surface directly, and they faced severe challenges involving large deformations. A weak point of the Euler grid method is the numerical diffusion in the discretization of the advection term (Gotoh and Sakai, 1999). The difficulty of meshing techniques for complex structures remains a problem without effective solutions.

Over the past two decades, particle methods have been developed as new numerical methods. They are mainly divided into two categories: the smoothed particle hydrodynamics (SPH) method and the moving particle semi-implicit (MPS) method. The traditional SPH method uses an explicit algorithm to simulate fluid flow. By contrast, the MPS method uses a semi-implicit method for modeling. Particle methods are full Lagrangian methods, which do not require the use of any mesh. Fluid is represented by a finite number of particles. Each particle has physical properties, such as position, mass, velocity, and pressure. As a result of its Lagrangian nature, free surface flow can be obtained directly without any special treatment. As it is mesh free, the SPH method facilitates the modeling of complex geometric structures, such as an armor blocks. Thus, the SPH method is widely used for the violent surface motion of the fluid-structure interaction.

The SPH method originated from the simulation of astrodynamics in the 1970s (Lucy, 1977). To expand the application of the SPH method to the field of hydrodynamics, many scholars have proposed a series of modifications and corrections aimed at improving the accuracy and stability of numerical calculations. The efforts to improve the accuracy of the SPH method have mainly focused on reducing the nonphysical oscillations generated during particle interactions. Impressive work, such as the development of the delta-SPH model (Molteni and Cola- grossi, 2009; Antuono, 2012) and the Riemann SPH method (Monaghan, 1997; Gao, 2012), has enhancedthe accuracy of the pressure field, as well as the completeness and consistency (Liu and Liu, 2006). Numerical instability can be categorized into two major categories, namely, rank deficiency and stress state instability (Beissel and Belytschko, 1996; Gotoh and Khayyer, 2016). The criterion of the maximum time step in the weakly compressible smoothed particle hydrodynamics (WCSPH) was suggested by Morris(1997) and Violeau and Leroy (2014). A number of studies have minimized the probability of tensile instability, including artificial repulsive forces (Monaghan, 1992, 2000), corrective functions for kernel estimates (Dilts, 1999), and conservative smoothing (Hicks and Liebrock, 2004).

In coastal engineering, the SPH method has been widely used in wave generation and absorption (Heller, 2016; Altomare, 2017), wave propagation (Altomare, 2015b), wave breaking (Gotoh and Sakai, 1999; Farahani and Dalrymple, 2014), wave run-up (Shadloo., 2015), overtopping (Gotoh, 2005; Shao, 2006), wave-structure interaction (Sarfaraz and Pak, 2017a; Verbrugghe, 2018), and porous flow (Ren, 2014, 2016). Thefluid-structure interaction is an important direction in SPH research. The main treatment methods for such interaction are the coupling of SPH and Finite Element Method (SPH-FEM) (Yang, 2012) and coupling of SPH and Discrete Element Method (SPH-DEM) (Canelas, 2016; Tang, 2018).

Breakwaters are important coastal structures that can utilize armor blocks, caissons, and core stones. A literature review was performed on the interaction between waves and breakwaters based on the SPH method. Ren(2013) proposed a 2D DEM-SPH model for simulating the movement of armor blocks on a rubble-mound breakwater under wave action and evaluated the hydraulic stability of the armor blocks. Altomare(2014) simulated the interaction between periodic waves and a Zeebrugge breakwater on the basis of DualSPHysics. Antifers were used as an armor layer and arranged in three regular permutations. Altomare(2017) simulated the interaction of irregular waves and a vertical breakwater with and without AWAS and validated the results with experiments. Sarfaraz and Pak (2017b) used an integrated SPH-polyhedral DEM algorithm to evaluate the stability of a cubic armor in a slope breakwater with different geometric sections and wave conditions. Then, the same method was used to analyze the stability of the cubic armor in a low-crest breakwater. A nondimensional equation was proposed on the basis of extensive calculations, and the results showed that stability s related to wave steepness, length of the free bore, and cubic side (Sarfaraz and Pak, 2018).

Under extreme circumstances, such as high water level and large wave height, breakwaters are subjected to a large force and are prone to damage. At the same time, waves easily cross the top of a breakwater, and an overtopping flow is produced. This flow continues, and secondary waves are generated after the breakwater. Although these secondary waves obviously weaken after the breakwater as a result of breakwater resistance, the wave state in the port is still changed. Such variation exerts an effect on docked ships. Under extreme conditions, the wave height in a harbor is large, and the cables of ships may even break. The existing research on secondary waves has mainly focused on the transmission waves of submerged breakwaters. The general understanding is that secondary waves are partially caused by the transfer of weak nonlinear dissipative waves and high-frequency energy generation. Beji and Battjes (1993) found that high-frequency energy is generated when waves pass over a bar. Wave energy is transformed into high-frequency energy. No obvious relationship exists between wave spectrum evolution and wave breaking type. Masselink (1999) presented two stages of secondary wave generation: 1) phase-bound harmonic energy generation and 2) decoupling of high-frequency energy. Sénéchal(2001) found that wave breaking weakens the nonlinearity of the coupling of different frequencies but that it exerts little effect on the process of energy transfer to a high frequency. The decoupling process occurs after a breakwater is submerged, and it is not entirely due to the increase in water depth and the deshoaling effect (Sénéchal, 2002). Li and Yu (2009) found that the energy of regular and irregular waves crossing a slope bar is transferred to a high frequency, thereby causing a drastic change in the spectrum shape. The reflection increases, and high-frequency energy decreases at the upslope of the bar. Kuznetsov and Saprykina (2012) found that a high-frequency wave is generated after a wave passes a submerged breakwater and that it leads to a reduction in the mean period. This phenomenon is especially pronounced when the wave crosses multiple submerged levees. Saprykina(2015) found that a solid submerged bar could effectively reduce the mean period and that a permeable bar could significantly reduce wave height. The research on secondary waves generated by overtopping is limited. Thus, the current work focuses on the wave pressure of the interaction between irregular waves and a vertical breakwater, as well as the secondary waves generated by overtopping. This study considers the secondary waves generated by overtopping and the energy evolution during wave propagation.

The paper is organized as follows. Sections 2 and 3 describe the WCSPH numerical method and experiments, respectively. On the basis of the premise that the WCSPH solution is the superimposition of an incompressible solution with acoustic components, Section 4 shows how filtering techniques, such as wavelet transform (WT), can be adopted to remove acoustic components. Numerical solutions and experimental results are compared, and the wave forces on a caisson are discussed. Section 5 presents the analysis of the secondary waves generated by overtopping and their evolution.

2 SPH Method

The SPH method is a full Lagrangian and meshless numerical method. The computing domains are discretized into a set of particles. The method constructs an approximation function through discrete points and solves the integral equation or differential equation of field variables with various boundary conditions, such as density, velocity, and pressure.

2.1 Basic Principle of SPH

Discretization schemes based on SPH have two basic steps: kernel approximation and particle approximation. Kernel approximation is used to represent a function and its derivatives in a continuous form as an integral representation using the kernel function and its derivations. The approximation value ofat positioncan be written as follows:

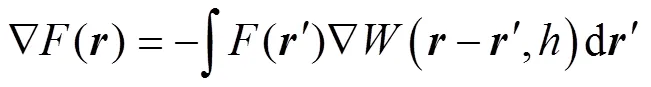
where() is the approximate value at positionin the computational domain.is a kernel function that is approximated by a Dirac function, andis the smoothing length.(−,) represents the weight contribution of positionto positionin the support domain. Therefore,() is a weighted integral interpolation.

In the particle approximation, the computational domain is discretized with a set of particles, and the integral equation is transformed into a discrete summation form. This step is used to discretize Eq. (1) and Eq. (2) using particles. The() value of particleis determined by all the particles in its support domain.

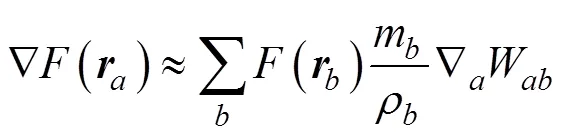
where particleis relative tom/ρof the neighbor particle andandare the mass and density, respectively.Wrepresents the weight contribution of particleto positionin the support domain. Eq. (3) and Eq. (4) provide a numerical discrete method to solve the partial differential equation by using the kernel function.

The kernel function should satisfy a number of basic requirements, such as the normalization condition, compact support, and Dirac function behavior (Liu and Liu, 2003; Liu, 2003).It comes in many forms, with the most commonly used being the cubic and quantic forms. In the current work, the following quantic kernel function is employed:

where=/andα=7/(14π2)has a constant value in two dimensions.

2.2 Governing Equation and Its Discrete Form

The SPH method is a Lagrangian mesh-free method. It relies on the Lagrangian form of the Navier-Stokes equations, which are written as follows:

where,,, anddenote the time, velocity, pressure, and viscosity, respectively; andis the body force per unit mass. Using Eq. (3) and Eq. (4), Eq. (6) and Eq. (7) can be respectively transformed into the following SPH discrete forms:

2.3 State Equation

In the WCSPH method, an artificial compressibility technique is usually used to simulate an incompressible flow as a slightly compressible flow. Therefore, the following state equation is used to describe the relationship between the density and the pressure in a quasi-incompressible flow:

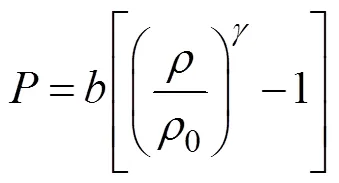
whereis the Courant number, which is a constant in the order of 0.1 (Gómez-Gesteira, 2010). The explicit time integration scheme for the time step is defined by. The first term considers the force magnitudes, and the second term is a viscous diffusion term.

2.4 Delta-SPH Formulation

The delta-SPH model is adopted in the calculations to reduce the pressure oscillation caused by the state equation. The delta-SPH model introduces a dissipation term in the continuity equation. The formula is as follows:

whereΦis a parameter that needs to be appropriately selected; herein, 0.1 is adopted. In the fluid region, Eq. (13) expresses an accurate diffusion.

2.5 Boundary Condition

In SPH, the boundary condition is expressed by a set of particles that separate from fluid particles. The dynamic boundary condition (DBC) was proposed by Crespo(2007). In this method, boundary particles and fluid particles have the same properties, such as mass, density, and velocity. They also satisfy the governing equations of fluid mechanics. However, boundary particles do not move, or they move with a given motion. When the distance between the fluid and the boundary particles is less than 2, the density and pressure of the boundary particles increase. Therefore, the repulsive forces of the fluid particles and boundary particles increase simultaneously to prevent fluid particles from passing through. DBC has been verified to be capable of effectively simulating the interaction between waves and structures (Altomare, 2014, 2017).

3 Experimental Model Setup

Experiments were performed at the Tianjin Research Institute for Water Transport Engineering, Port Hydraulic Engineering Technology, National Engineering Laboratory Wind Wave Flume. The flume measured 68m in length, 1m in width, and 1.5m in height (Fig.1). The right side of the flume was equipped with a piston-type wave maker, which can generate regular waves and irregular waves on the basis of the JONSWAP spectrum. A sponge was provided at the left end of the flume to absorb waves and prevent wave reflections. Fig.2 shows a cross section of a vertical breakwater that was placed 35m from the piston. It was a chamfered vertical breakwater with a height of 0.98m and chamfering slope of 1:1.67. Armor block and stone were used to protect the breakwater from erosion (Fig.3). In measuring the wave force, 24 pressure transducers were arranged in a caisson (Fig.4). An SG2008wave pressure acquisition system with an acquisition frequency of 50Hz was adopted. Sensors #1–#6 were used to measure the uplifting force, #7–#18 were used to measure the horizontal force, and #16–#24 were used to measure the downward force caused by overtopping. The coordinates of the pressure transducers are presented in Table 1.

The experiments were carried out with irregular waves by using the JONSWAP spectrum with a peak enhancement factor=3.3. The wave conditions are listed in Table 2, and the wave making time was 130 mean periods. The relationship between the peak periodpand the mean periodmis shown in Eq. (14).

Fig.2 Sketch of experimental setup.

Fig.3 Vertical breakwater section.

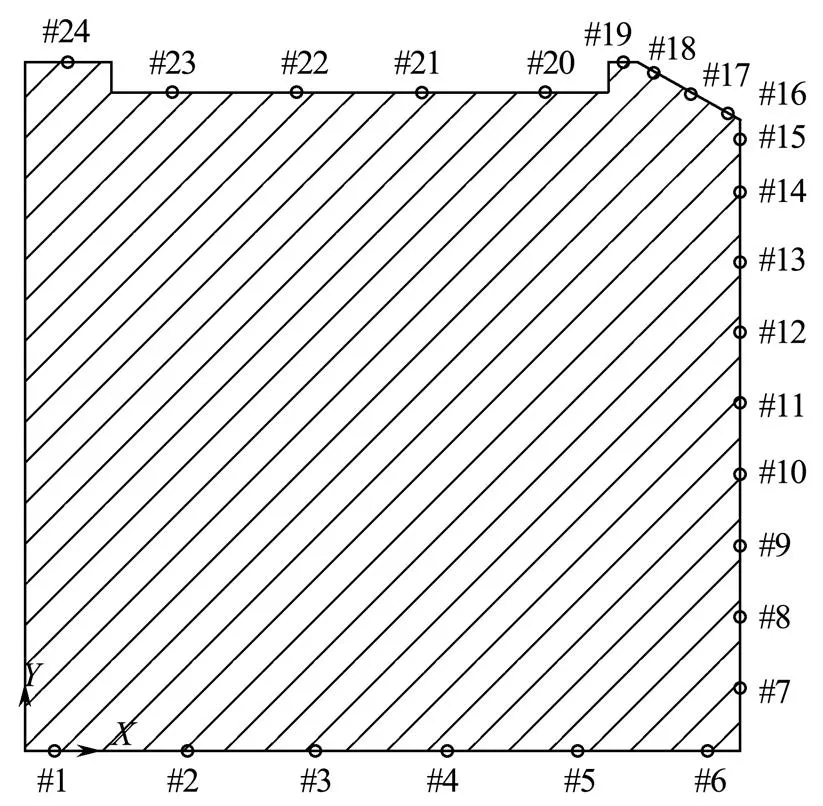
Fig.4 Arrangement of measurement points.

Table 1 Coordinates of pressure sensors

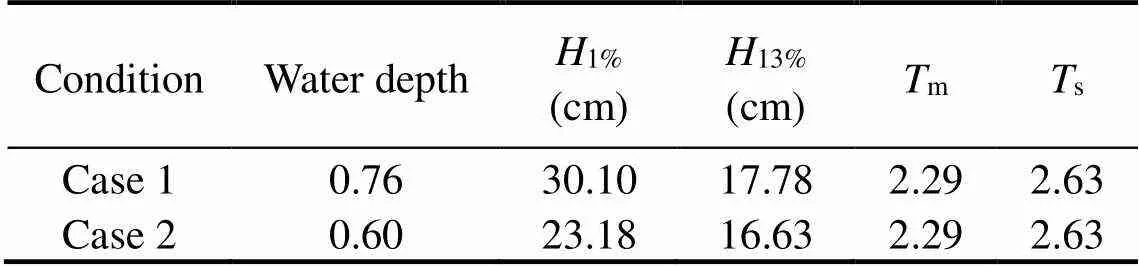
Table 2 Wave conditions

4 Numerical Wave Making Test

A two-dimensional numerical wave tank was used to simulate wave propagation. The JONSWAP spectrum was adopted for the experiments. The shape of the spectrum was defined by the spectral peak. The method of Liu and Frigaard (2001) was used to generate irregular waves by implementing a first-order wave generation algorithm: the irregular wave train was generated by combining the discrete amplitude wave spectra corresponding to the target wave energy spectra with random phases obtained by a random number generator (Altomare, 2017).

On the basis of the Biesel transfer functions, the free surface elevation is converted into the motion of the piston:

After the piston stroke, angular frequency, and initial phase of each regular wave are defined, the time series of the piston for irregular waves can be given:

wherek,ω, andεdenote the wave number, angular velocity, and initial phase of the component waves, respectively.

The total energy is divided into 120 parts. Fig.5 shows the energy bisection results.

The length of the numerical wave tank (NWT) was set to 38m to reduce the amount of calculation. The piston was set at=0m. Wave elevation gauges were located from 19m to 21m at intervals of 0.5m (Fig.6). As the average period was relatively large, the generated waves could break near the piston. To prevent wave breaking near the wave piston, we increased the water depth by 20cm and built the breakwater on a submerged levee structure, which had a height of 20cm. Fig.7 shows the surface elevations at=20m for case 1 and case 2. The wave characteristic parameters were calculated and compared with the those of the target waves, and the relative errors are listed in Table 3. The fast Fourier transform (FFT) method was used to analyze the elevation signal and obtain the energy spectrum. A comparison of the computational spectrum and theoretical spectrum is shown in Fig.8. The irregular wave spectrum simulated by SPH is basically consistent with the theoretical spectrum. Hence, the program could simulate irregular waves on the basis of the JONSWAP spectrum.

Fig.5 Energy bisection results for case 1 (a) and case 2 (b).

Fig.6 Sketch of NWT for verifications.

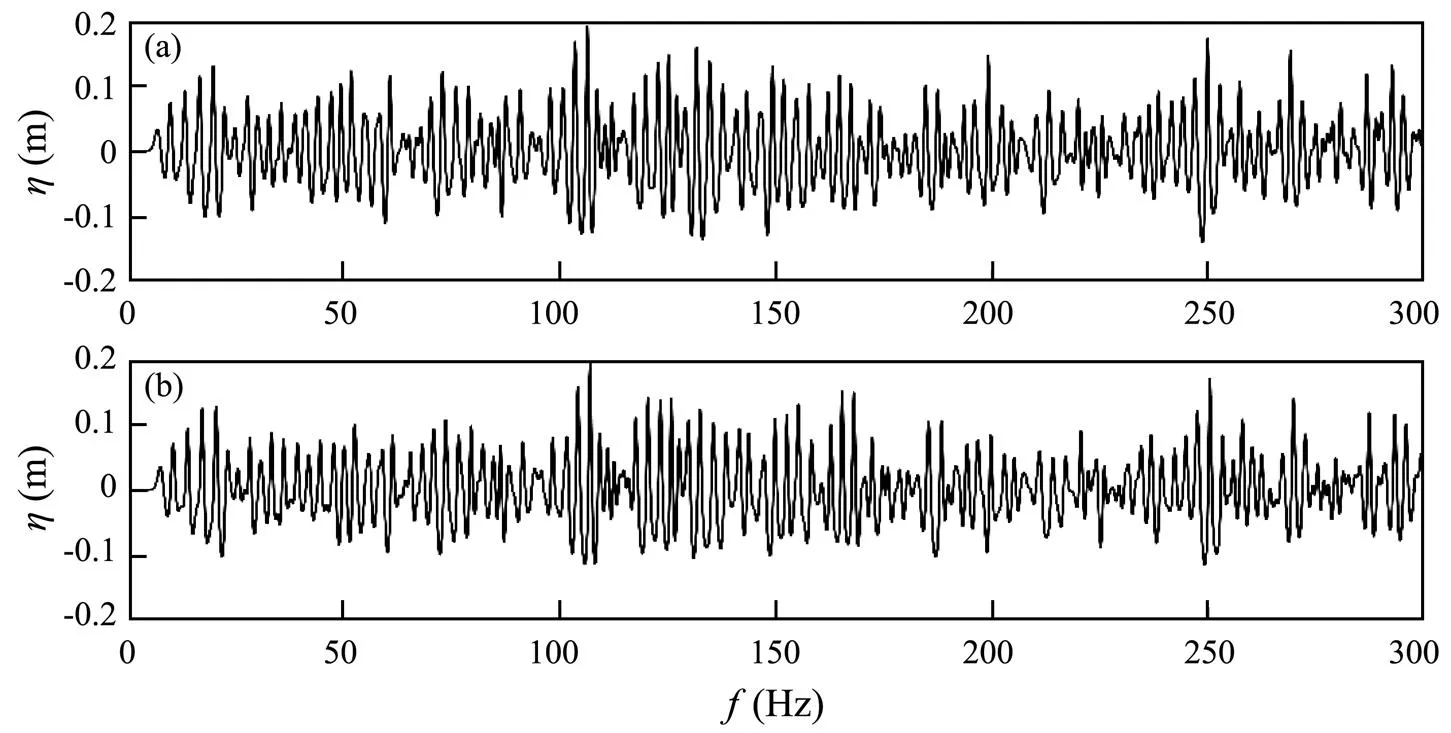
Fig.7 Numerical wave gauge values at x=19m in case 1 (a) and case 2 (b).

Fig.8 Comparison of theoretical and numerical spectra.

Table 3 Numerical wave making errors

5 Interaction of Irregular Waves with Vertical Breakwater

5.1 Model Establishment

A vertical breakwater was established on a submerged levee, and its right end was set at=12.9m. Given the large water depth, the armor block was underwater during the whole process. In simplifying the numerical model, a circular permeable structure was used to represent the Accropodes, stone blocks, and core stones to indicate its interaction with the water and porous flow effect (Fig.9). To prevent the water level in front of the breakwater from decreasing because of overtopping, we set a return channel below the bottom of the physical flume connecting the back and front water of the breakwater. In the numerical wave flume, the return channel was set under submerged slope as the physical model tests.

Fig.9 Drawing of vertical breakwater model.

5.2 Wave-Vertical Breakwater Interaction in Case 1

Under case 1, the high water level was close to the top of the breakwater. The main characteristic of the interaction between the waves and the vertical breakwater was overtopping. As the water level was close to the top of the breakwater, waves rose before the breastwork and overtopped it (Figs.10(a), (b)). A continuous flow was generated on top of the breakwater (Figs.10(c), (d), (e)), and it broke behind the breakwater (Fig.10(f)). Even though the wave breaking was obvious, it exerted little effect on the foundation bed because of the high water level. The armor remained stable throughout the interaction.

5.3 Wave-Vertical Breakwater Interaction in Case 2

Under case 2, the waves and vertical breakwater showed two types of interaction. The first type was similar to the high water level; that is, the waves did not change significantly before reaching the breakwater and attacking the caisson. When the wave height was large, upward splashing occurred during the impact, and overtopping became likely. By contrast, when the wave height was small, no breaking occurred. In the second type of interaction, a plunging wave was generated, and it attacked the caisson. When the wave propagated to the toe, the wave depth became small, thereby causing wave deformation. Waves became steep, and they tilted in the forward direction, as shown in Fig.11(a). When the wave moved to the fundamental bed, the wave tilted in the forward direction obviously, and a plunging wave was generated (Fig.11(b)); the plunging wave hit the caisson and broke (Fig.11(c)). Waves ran up along the chamfered breastwork and caused high splashing (Fig.11(d)). Then, they fell on the top of the breastwork (Figs.11(e), (f)).

Fig.10 Comparisons of instantaneous wave surfaces between predicted and experimental results at high water levels.

Fig.11 Comparisons of instantaneous wave surfaces between predicted and experimental results at low water levels.

5.4 Postprocessing of Pressure Signals

The WCSPH numerical solution is disturbed by acoustic waves, which are generated by numerical oscillations. These acoustic waves should be removed. In recent years, different methods have been proposed to remove high-frequency acoustic waves from WCSPH pressure solutions. Colagrossi and Landrini (2003) introduced a non-conservative method for periodic density reinitialization. Later on, a conservative diffusion term was introduced to the continuity equation(Molteni and Colagrossi, 2009). Other scholars have solved particle interactions by using accurate or approximate Riemann solvers (Marongiu, 2010; Koukouvinis, 2013). These modified methods make the numerical SPH results increasingly reliable, but they are implemented in the kernel support domain, and pressure field noise still exists.

The delta-SPH model was adopted in the present work, and the pressure results needed to be denoised. At a Mach number tending toward zero, the WCSPH solution consists of an incompressible SPH solution and high-frequency noise(Munz, 2003; Seo and Moon, 2006). The superimposition of these two components is the basis of subsequent analyses. Therefore, the filtering process is an important step in processing WCSPH solutions. Specifically, filtering can remove acoustic waves and the energy evolution caused by high-frequency noise. In the current study, WT was adopted to process the pressure signals generated during the interaction between irregular waves and the vertical breakwater. The premise for using this filtering method is that the Mach number should be small enough to ensure that the noise frequency is significantly higher than the incompressible frequency. This section shows the filtered results for the pressure gauge measurements at two points (#1 and #13).

The WT method was proposed by Morlet in seismic data analysis research, and a continuous CWT was developed thereafter (Morlet, 1983; Grossmann and Morlet, 1984). After decades of advancement, the WT method has become an important analysis method. It can simultaneously consider variations in the time and frequency domains to capture the local characteristics of signals, which can be applied to stationary and nonstationary processes. Farge (1992) adopted the Morlet wavelet to analyze turbulence. The Morlet wavelet and Morr (Mexican hat)wavelet, which are commonly used in fluid dynamics(Wang, 2007; Schneider and Vasilyev, 2010;Li., 2015), have been adopted to filter WCSPH solutions and successfully separate high-frequency noise(Meringolo, 2017).Aristodemo(2017) studied the wave force during the interaction of solitary waves and horizontal circular cylinders on the basis of experiments and the WCSPH model. The WT was used to filter the acoustic waves by a cutoff frequency.

The WT of() can be defined by the following expression:

whereandare the scale and translation parameters, respectively; the asterisk represents the complex conjugate; and() denotes the mother wavelet.

In the wavelet framework, a shape function that is commonly used in fluid dynamics is the Morlet wavelet, which was adopted in this work to study the characteristics of pressure signalSPH. It is defined as follows:

where0is the central frequency.The Morlet wavelet is the relationship between its scale parameter and the Fourier period given by Torrence and Compo (1998); it is given as follows:

where0=6.2 andis approximately equal to.

When a wave impacts a structure, an extremely short time pressure pulse is generated. Moreover, the acoustic components and incompressible components are difficult to decompose. To filter the spurious acoustic components, Aristodemo(2017) provided the following cutoff frequency:

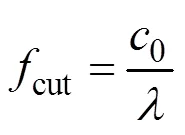
The equation represents the lowest frequency at which spurious acoustic oscillations arise in a pressure solution; here,0is the initial sound speed, andis associated with the length of the numerical flume=2L. The numerical oscillations linked to the acoustic components appear in the frequency band ranging frommin=∆0/2tocut. The selected spatial resolution and artificial sound speed ensure a good separation between the physical pressure solution and numerical noise. The inverse continuous wavelet transform (ICWT) was then used to reconstruct the filtered signal. Fig.12 shows the wavelet coefficients of the pressure oscillation obtained from SPH. In this case, significant acoustic noise was encountered in the SPH solution in the range of frequencies. The noise appeared to be practically uniform along the oscillation period and could be clearly distinguished from the energy content of the WT related to the incompressible pressure signal. Fig.12(a) and Fig.12(b) show the magnitude scalograms of #1 of case 2 and the filtered results. A significant oscillation appeared in the high-frequency energy. A small amount of energy was also present for the high frequencies, and it was due to the residual error of the WT-ICWT cycle. Fig.12(c) shows the results reconstructed using ICWT, and it indicates that the high-frequency acoustic noise was filtered out of the original signal.

During the interaction between the waves and the vertical breakwater, the pressure gauges near the water surface, such as #13, were sometimes immersed in the water or exposed. In numerical calculations, high-frequency and large-amplitude acoustic perturbations are generated when pressure gauges are alternately immersed and exposed. A high-frequency pressure signal is also generated when the waves attack the caisson. Fig.13(a) shows the original wavelet coefficient. As the form of the oscillation was different from that of #1, the following newcutwas proposed to filter the acoustic components:

Relative to Fig.13(a), Fig.13(b) shows the removal of the high-frequency and large-amplitude components. Fig.13(c) shows the WT-filtered signal. The oscillation at an abrupt change in pressure was significantly reduced. When the pressure gauge was exposed to air, the characteristics at a pressure of zero were retained.

The wavelet filtered results for 24 pressure points were obtained. Then, the wave force values for case 1 and case 2 were calculated. Fig.14 and Fig.15 show the pressure distribution when the horizontal force reached its maximum. The pressure distributions of the experimental and numerical results were basically the same. In case 2, #10,which was located in the vertical caisson face, showed a concave value because of wave impacting. Fig.16 presents the time histories of the #7–#16 pressure sensors under low water levels. The black lines in the figure represents the pressure history of each sensor. The red dotted line represents the moment when the horizontal force reaches its maximum. The pressure history shapes of #7–#15 revealed an impact wave load. The pressure of #10 was smaller than the pressure of #9 and #11.

The forces on the caisson are listed in Tables 4 and 5. Although the mean periods of the two cases were the same and the significant wave height of case 1 was higher than that of case 2, the maximum horizontal force of case 1 was smaller than that of case 2. Its value was 319.0N smaller in the experiments and 204.6N smaller in the numerical results. When the horizontal force was at its maximum, the uplifting force of case 2 was significantly higher than that of case 1. The uplifting force differences between case 1 and case 2 were 281.2N in the experiments and 232.3N in the numerical simulations. The permeability model proposed in this work simulated the uplifting force of the caisson, but obvious differences were noted between the numerical simulation and the experimental results. In case 1, the numerical value was 85.2N larger than the experimental value. However, the numerical value was 48.9N smaller than the experimental value in case 2. These differences were due to the fact that the porous structure was a simplified form of cork and armor and that the forces exerted by the boundary particles created a small gap between the boundary and the fluid particles. Therefore, the actual permeability was different from the set permeability. When the horizontal force was at its maximum, the uplifting force was close to the maximum value of the uplifting force during the whole experiment. In the case of a low water level, the vertical breakwater was subjected to the greatest force. Given the low water level, waves were significantly deformed. Wavesmoved forward against the caisson, resulting in wave breaking. Moreover, because of the low water level, the disturbance of the foundation by waves was considerable, thereby resulting in a relatively large uplifting force on the caisson.

Fig.12 Case 2 #1: (a) original magnitude scalograms, (b) filtered magnitude scalograms, (c) WT-filtered signal (original signal: black dashed line; WT signal: red solid line).

Fig.13 Case 2 #13: (a) original magnitude scalograms, (b) filtered magnitude scalograms, (c) WT-filtered signal (original signal: black dashed line; WT signal: red solid line).

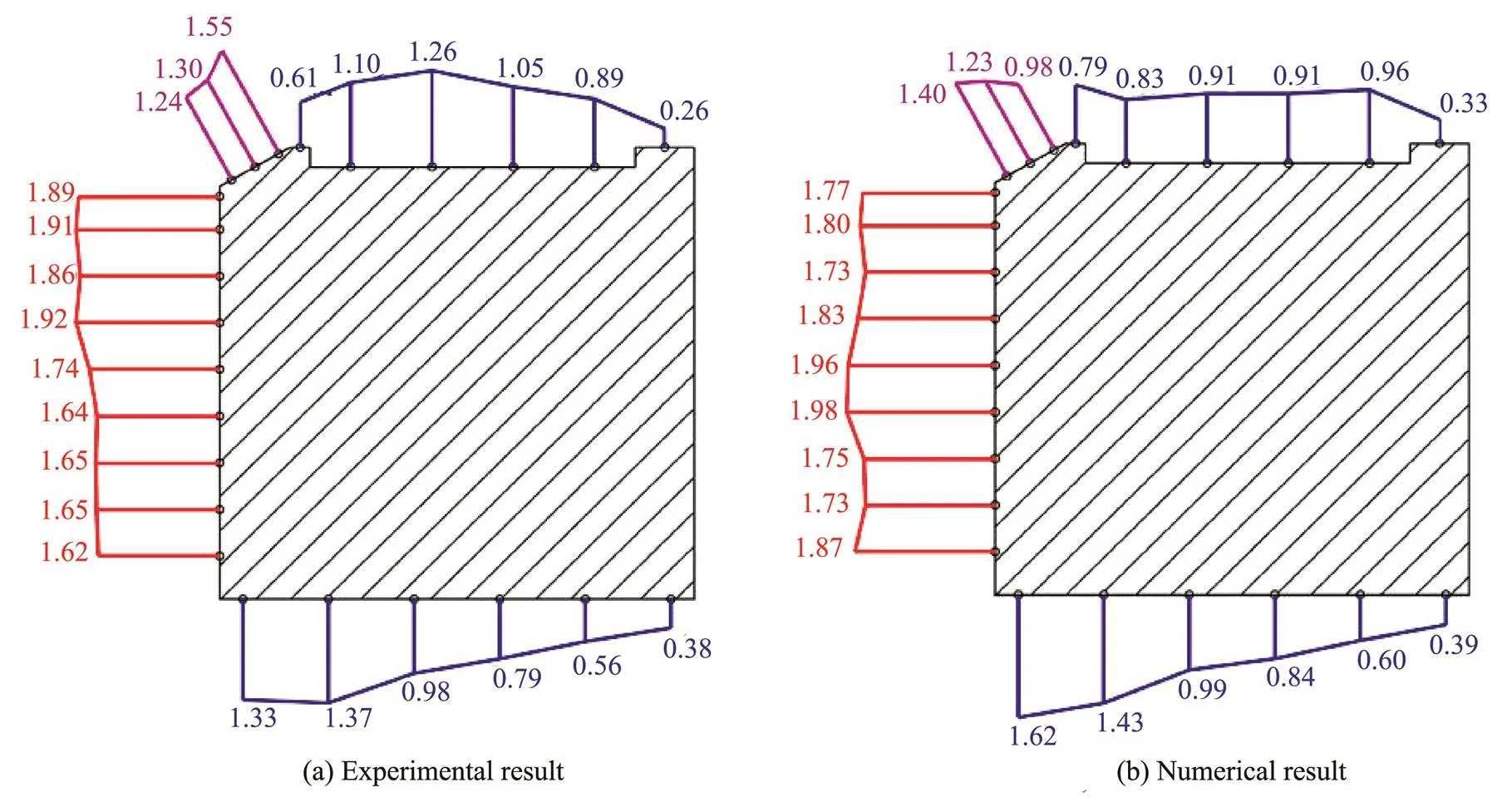
Fig.14 Pressure of each gauge in case 1 as horizontal force reaches maximum.

Fig.15 Pressure of each gauge in case 2 as horizontal force reaches maximum.

Fig.16 Pressure histories of #7–#16 under low water levels.

Table 4 Maximum horizontal force, uplifting force, and downward force in case 1

Table 5 Maximum horizontal force, uplifting force, and downward force in case 2

6 Secondary Wave Analysis

As a result of overtopping, waves pass through breakwaters and spread behind them, thus affecting the wave condition and ships in harbors. Previous studies on secondary waves have focused on waves crossing submerged breakwaters. Waves moving over submerged breakwaters shift energy to high frequencies, and the energy spectrum produces a bimodal form. This section analyses the secondary waves behind a breakwater caused by overtopping and the evolution of secondary wave propagation.

In physical tests, five wave elevation gauges were arranged behind the breakwater. The distance between thegauges was 0.5m (see Fig.2). The FFT method was used for the experimental data from the five gauges (Fig.17(a)). Two main harmonics were noted. The first harmonic was 0.3512Hz, which was consistent with the peak frequency of the incident waves. The second harmonic generated was located at 0.7043Hz. Fig.17(a) shows that significant energy transfers to high frequencies, particularly to the second harmonic, occurred behind the breakwater. As shown in Fig.17(b), the energy of the first harmonic was still the main component as the waves propagated. The energy of the second harmonic was the least. In WG4, the energy of the second harmonic was the greatest.

The SPH model was used to describe in detail the evolution of secondary waves after the breakwater. A total of 24 wave gauges were located in a range of 21–32.5m. The distance between the wave gauges was 0.5m. As a velocity damping zone was set at the right end, reflection was avoided. Fig.18(a) shows how the spectrum changed with the propagation direction. Two main peaks were noted in the spectrum, and they revealed the energy transfers to high-frequency harmonics. In the numerical simulation, two main harmonics were also established. The first harmonic was 0.3396Hz, and the second harmonic was 0.6650Hz; these values were close to the experimental results. With wave propagation, the energy of the first harmonic varied greatly, and the energy of the second harmonic remained stable. The energy of the second harmonic was lower than that of the first harmonic. To analyze the influence of water depth on the secondarywaves after the breakwater, we simulated the secondary waves with different depths. The spectral analysis results are shown in Fig.18. The four depths were 0.96, 0.92, 0.88, and 0.84m; and the wave conditions of each depth were the same as those in case 1. As the water depth decreased, the energy behind the breakwater decreased. When=0.84m, the magnitude of the spectral peak density was less than 0.0006 (Fig.18(d)). This result indicated that overtopping rarely occurred. As shown in Figs.18(a)–(c), the first and second harmonics were basically the same with depth variation. The bandwidth of the first harmonic increased with the decrease of water depth. In the process of wave propagation behind the breakwater, the spectral density value of the first harmonic changed, and the value of the second harmonic was stable.

Fig.17 Spectrum evolution of experimental data.

Fig.18 Spectrum evolution of numerical simulation data.

The following conclusions were obtained on the basis of the physical test and numerical simulation results. 1) The wave spectrum behind the breakwater had two main peaks. The first harmonic was the peak frequency of the incident wave, and the wave energy was transferred to high-frequency harmonics. 2) Numerical calculation could simulate the phenomenon of energy transfer to high frequencies. The first and second harmonics were close to the experimental results. The spectrum density difference between the numerical and experimental results was related to the fact that the physical gauges were close to the breakwater and that artificial viscosity is a simplified turbulent model, which cannot reproduce real turbulent motion. 3) The comparison of spectra with different depths showed that the wave energy decreased as the depth decreased. Under the same wave condition, the first and second harmonics did not change with depth.

7 Conclusions

This study used experiments and numerical simulations to investigate the interaction between irregular waves and a vertical breakwater. The horizontal force, uplifting force, and downward force under different wave and depth conditions were calculated. The secondary waves generated by overtopping were also studied. In addition, the energy distribution of the secondary waves and the energy evolution along the propagation direction were analyzed. The conclusions can be summarized as follows.

1) The interaction of irregular waves and the vertical breakwater was simulated using the SPH method. The delta-SPH model was adopted to reduce pressure oscillations. A structure was introduced to represent permeability. In the post processing, the WT methods were used to filter the acoustic waves. The filtered numerical results and the experimental data were compared. The horizontal force results showed good agreement. However, the uplifting did not show a good fit because the permeable structure did not truly represent the flow between core stones. Nevertheless, it could simulate the uplifting force of a caisson.

2) The comparison of the wave forces for high water levels (case 1) and low water levels (case 2) showed that the horizontal force on the caisson was larger under the latter case than under the former case. When waves propagated to the toe of the breakwater, plunging waves were formed because of the shallow water effect. Then, these plunging waves attacked the caisson and broke. Large impact pressure was produced. Under the high water level condition, the distance between the water level and the top of the breakwater was 4cm, which facilitated overtopping. Wave breaking occurred behind the breakwater.

3) Under the high water level condition, wave overtopping frequently occurred, and secondary waves were generated after the breakwater. The analysis of the power spectra of the secondary waves showed that the energy transferred to high-frequency harmonics, with two main peaks emerging in the power spectrum. The first harmonicwas the incident crest frequency, which was still the dominant component. With wave propagation, the energy of the first harmonic varied greatly, whereas the energy of the second harmonic remained stable. The comparison of the spectra with different depths showed that the wave energy decreased as the depth decreased. Under the same wave conditions, the first and second harmonics did not change with depth variation.

Acknowledgements

The study was supported by the National Natural Science Foundation of China–Shandong Joint Fund (No. U1706226), the National Natural Science Foundation of China (No. 51779236), and the Key Science and Technology Projects of International Cooperation of Ministry of Transport, China (Nos. 2019-GH-002, TKS190304).

Allsop, N. W. H., and Vicinanza, D., 1996. Wave impact loadings on vertical breakwaters: Development of new prediction formulae.. Antwerp, 275-284.

Allsop, N. W. H., Kortenhaus, A., Oumeraci, H., and McConnell, K., 1999. New design methods for wave loading on vertical breakwaters under pulsating and impact conditions.. Santander, 595-602.

Allsop, N. W. H., McKenna, J. E., Vicinanza, D., and Whittaker, T. T. J., 1996. New design methods for wave loadings on vertical breakwaters and seawalls.. Orlando, 2508-2521.

Altomare, C., Crespo, A. J. C., Domínguez, J. M., Gómez-Gesteira, M., Tomohiro, S., and Verwaest, T., 2015a. Applicability of smoothed particle hydrodynamics for estimation of sea wave impact on coastal structures., 96: 1-12.

Altomare, C., Crespo, A. J. C., Rogers, B. D., Domínguez, J. M., Gironella, X., and Gómez-Gesteira, M., 2014. Numerical modelling of armour block sea breakwater with smoothed particle hydrodynamics., 130: 34-45.

Altomare, C., Domínguez, J. M., Crespo, A. J. C., Gonzáles-Cao, J., Suzuki, T., Gómez-Gesteira, M.,, 2017. Long-crested wave generation and absorption for SPH-based DualSPHysics model., 127: 37-54.

Altomare, C., Domínguez, J. M., Crespo, A. J. C., Suzuki, T., Caceres, I., and Gómez-Gesteira, M., 2015b. Hybridization of wave propagation model SWASH and meshfree particle method SPH for real coastal applications., 57 (4): 1550024-1-1550024-34.

Antuono, M., Colagrassi, A., and Marrone, S., 2012. Numerical diffusive terms in weakly compressible SPH schemes., 183 (12): 2570-2580.

Aristodemo, F., Tripepi, G., Meringolo, D. D., and Veltri, P., 2017. Solitary wave-induced forces on horizontal circular cylinders: Laboratory experiments and SPH simulations., 129: 17-35.

Bagnold, M. R. A., 1939. Interim report on wave pressure research., 12: 202-226.

Beissel, S., and Belytschko, T., 1996. Nodal integration of the element-free Galerkin method., 139: 49-74.

Beji, S., and Battjes, J. A., 1993. Experimental investigation of wave propagation over a bar., 19: 151-162.

Canelas, R. B., Crespo, A. J. C., Domínguez, J. M., Ferreira, R. M. L., and Gómez-Gesteira, M., 2016. SPH-DCDEM model for arbitrary geometries in free surface solid-fluid flows., 202: 131-140.

Chan, E. S., and Melville, W. K., 1988. Deep-water plunging wave pressures on a vertical plane wall., 417 (1852): 95-131.

Colagrossi, A., and Landrini, M., 2003. Numerical simulation of interfacial flows by smoothed particle hydrodynamics., 191 (2): 448-475.

Crespo, A. J. C., Gómez-Gesteira, M., and Dalrymple, R. A., 2007. Boundary conditions generated by dynamic particles in SPH methods., 5 (3): 173-184.

Dilts, G. A., 1999. Moving least squares hydrodynamics: Consistency and stability., 44: 1115-1155.

Enrigh, T. D., Fedkiw, R., Ferziger, J., and Mitchell, I., 2002. A hybrid particle level set method for improved interface capturing., 183: 83-116.

Farahani, R. J., and Dalrymple, R. A., 2014. Three-dimensional reversed horseshoe vortex structures under broken solitary waves., 91: 261-279.

Farge, M., 1992. Wavelet transforms and their applications to turbulence., 24: 395-457.

Gao, R., Ren, B., and Wang, G. Y., 2012. Numerical modelling of regular wave slamming on subface of open-piled structures with the corrected SPH method., 34: 173-186.

Goda, Y., 1974. New wave pressure formulae for composite breakwater.Copenhagen, 1702-1720.

Goda, Y., 2000.2nd edition. World Scientific Publishing, Singapore, 132-144.

Gómez-Gesteira, M., Rogers, B., Dalrymple, A. R., and Crespo, A. J. C., 2010. State-of-the-art of classical SPH for free-surface flows., 48: 6-27.

Gotoh, H., and Khayyer, A., 2016. Current achievements and future perspectives for projection-based particle methods with applications in ocean engineering., 2: 251-278.

Gotoh, H., and Sakai, T., 1999. Lagrangian simulation of breaking waves using particle method., 41: 303-326.

Gotoh, H., Ikari, H., Memita, T., and Sakai, T., 2005. Lagrangian particle method for simulation of wave overtopping on a vertical seawall., 47 (2-3): 157-181.

Grossmann, A., and Morlet, J., 1984. Decomposition of Hardy functions into square integrable wavelets of constant shape., 15 (4): 723-736.

Harlow, F., and Welch, J. E., 1965. Numerical calculation of time-dependent viscous incompressible flow of fluid with a free surface., 8: 2182-2189.

Hattori, M., Arami, A., and Yui, T., 1994. Impact wave pressure on vertical walls under breaking waves of various types., 22: 79-114.

Heller, V., Bruggemann, M., Spinneken, J., and Rogers, B. D., 2016. Composite modelling of subaerial landslide-tsunamis in different water body geometries and novel insight into slide and wave kinematics., 109: 20-41.

Hicks, D. L., and Liebrock, L. M., 2004. Conservative smoothing with B-splines stabilizes SPH material dynamics in both tension and compression., 150: 213-234.

Higuera, P., Lara, J. L., and Losada, I. J., 2013. Simulating coastal engineering processes with OpenFOAM., 71: 119-134.

Hirt, C. W., and Nichols, B. D., 1981. Volume of fluid (VOF) method for the dynamics of free boundaries., 39: 201-225.

Hu, C. H., and Kashiwagi, M., 2009. Two-dimensional numerical simulation and experiment on strongly nonlinear wave-body interactions., 14 (2): 200-213.

Klammer, P., Kortenhaus, A., and Oumeraci, H., 1996. Wave impact loading of vertical face structures for dynamic stability analysis-prediction formulae.. Orlando, 2534-2547.

Kortenhaus, A., Oumeraci, H., Kohlhase, S., and Klammer, P., 1994. Wave induced up-lift loading of caisson breakwaters.. Kobe, 1298-1311.

Koukouvinis, P., Anagnostopoulos, J., and Papantonis, D. E., 2013. An improved MUSCL treatment for the SPH-ALE method: Comparison with the standard SPH method for the jet impingement case., 71: 1152-1177.

Kuznetsov, S., and Saprykina, Y., 2012. Secondary waves in coastal zone: Physical mechanisms of formation and possible application for coastal protection.Santander, 1-14.

Li, B., and Yu, X., 2009. Wave decomposition phenomenon and spectrum evolution over submerged bars., 28 (3): 82-92.

Li, J., Yang, J., Liu, S., and Ji, X., 2015. Wave groupiness analysis of the process of 2D freak wave generation in random wave trains., 104: 480-488.

Liu, G. R., and Liu, M. B., 2003.. World Scientific, Singapore, 32-48.

Liu, M. B., and Liu, G. R., 2006. Restoring particles consistency in smoothed particle hydrodynamics., 56 (1): 19-36.

Liu, M. B., Liu, G. R., and Lam, K. Y., 2003. Constructing smoothing functions in smoothed particle hydrodynamics withapplications.,155: 263-284.

Liu, Z., and Frigaard, P., 2001.. Aalborg University, Aalborg, 65-76.

Lucy, L. B., 1977. A numerical approach to the testing of the fission hypothesis., 82 (12): 1013-1024.

Marongiu, J. C., Leboeuf, F., Caro, J., and Parkinson, E., 2010. Free surface flows simulations in Pelton turbines using an hybrid SPH-ALE method., 48: 40-49.

Masselink, G., 1999. Field investigation of wave propagation over a bar and the consequent generation of secondary waves., 33: 1-9.

Meringolo, D. D., Colagrossi, A., Marrone, S., and Aristodemo, F., 2017. On the filtering of acoustic components in weakly-compressible SPH simulations., 70: 1-23.

Minikin, R. R., 1963.2nd edition. Charles Griffin, London, 92-103.

Molteni, D., and Colagrossi, A., 2009. A simple procedure to improve the pressure evaluation in hydrodynamic context using SPH., 180 (6): 861-872.

Monaghan, J. J., 1992. Smoothed particle hydrodynimics., 30: 543-574.

Monaghan, J. J., 1997. SPH and Riemann solvers., 136 (2): 298-307.

Monaghan, J. J., 2000. SPH without a tensile instability., 159 (2): 290-311.

Morlet, J., 1983. Sampling theory and wave propagation., 47 (4): 233-261.

Morris, J. P., Fox, P. J., and Zhu, Y., 1997. Modelling low Reynolds number incompressible flows using SPH., 136: 214-226.

Munz, C. D., Roller, S., Klein, R., and Geratz, K. J., 2003. The extension of incompressible flow solvers to the weakly compressible regime., 32: 173-196.

Nakamura, T., Tanaka, R., Yabe, T., and Takizawa, K., 2001. Exactly conservative semi-Lagrangian scheme for multi-dimensional hyperbolic equations with directional splitting technique., 174: 171-207.

Obhrai, C., Bullock, G., Wolters, G., Müller, G., Peregrine, H., Bredmose, H.,, 2004. Violent wave impacts on vertical and inclined walls: Large scale model tests.. Lisbon, 4075-4086.

Osher, S., and Sethian, J. A., 1988. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations.; 79 (1): 12-49.

Ren, B., Jin, Z., Gao, R., Wang, Y., and Xu, Z., 2013. SPH-DEM Modeling of the hydraulic stability of 2D blocks on a slope., 140 (6): 04014022.1-04014022.12.

Ren, B., Wen, H., Dong, P., and Wang, Y., 2014. Numerical simulation of wave interaction with porous structures using an improved smoothed particle hydrodynamic method., 88: 88-100.

Ren, B., Wen, H., Dong, P., and Wang, Y., 2016. Improved SPH simulation of wave motions and turbulent flows through porous media., 107: 14-27.

Saprykina, Y., Kuznetsov, S., and Korzinin, D., 2015. Nonlinear transformation of waves above submerged structures., 116 (1): 187-194.

Sarfaraz, M., and Pak, A., 2017a. An integrated SPH-polyhedral DEM algorithm to investigate hydraulic stability of rock and concrete blocks: Application to cubic armours in breakwaters., 84: 1-18.

Sarfaraz, M., and Pak, A., 2017b. SPH numerical simulation of tsunami wave forces impinged on bridge superstructures., 121: 145-157.

Sarfaraz, M., and Pak, A., 2018. Numerical investigation of the stability of armour units in low-crested breakwaters using combined SPH-Polyhedral DEM method., 81: 14-35.

Schneider, K., and Vasilyev, O. V., 2010. Wavelet methods in computational fluid dynamics., 42: 473-503.

Sénéchal, N., Bonneton, P., and Dupuis, H., 2001. Generation of secondary waves due to wave propagation over a bar: A field investigation., 1: 764-772.

Sénéchal, N., Bonneton, P., and Dupuis, H., 2002. Field experiment on secondary wave generation on a barred beach and the consequent evolution of energy dissipation on the beach face., 46 (3): 233-247.

Seo, J. H., and Moon, Y. J., 2006. Linearized perturbed compressible equations for low Mach number aeroacoustics., 218: 702-719.

Shadloo, M. S., Weiss, R., Yildiz, M., and Dalrymple, R. A., 2015. Numerical simulation of long wave runup for breaking and nonbreaking waves., 25 (1): 1-7.

Shao, S., Ji, C., Graham, D. I., Reeve, D. E., James, P. W., and Chadwick, A. J., 2006. Simulation of wave overtopping by an incompressible SPH model., 53 (9): 723-735.

Sogut, D. V., and Yalciner, A. C., 2019. Performance comparison of NAMI DANCE and FLOW-3D models in tsunami propagation, inundation and currents using NTHMP benchmark problems., 176: 3115-3153.

Sussman, M., and Puckett, E. G. A., 2000. Coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows., 162 (2): 301-337.

Takahashi, S., Tanimoto, K., and Shimosako, K., 1993. Experimental study of impulsive pressures on composite breakwaters-fundamental feature of impulsive pressure and the impulsive pressure coefficient., 31 (5): 33-72.

Takahashi, S., Tanimoto, K., and Shimosako, K., 1994. A proposal of impulsive pressure coefficient for design of composite breakwaters.. Yokosuka, 489-504.

Takewaki, H., Nishiguchi, A., and Yabe, T., 1985. The Cubic-Interpolated Pseudo-Particle (CIP) method for solving hyperbolic-type equations., 61: 433-444.

Tanaka, T., Nakamura, R., and Ysbe, T., 2000. Constructing exactly conservative scheme in a non-conservative form., 126: 232-243.

Tang, Y., Jiang, Q., and Zhou, C., 2018. A Lagrangian-based SPH-DEM model for fluid-solid interaction with free surface flow in two dimensions., 62: 436-460.

Tornberg, A. K., and Enhquist, B., 2000. A finite element based level set method for multiphase flow applications., 3: 93-101.

Torrence, C., and Compo, G. P., 1998. A practical guide to wavelet analysis., 79 (1): 61-78.

Tsai, C., Chen, Y., Chen, C., and Chang, L., 2016. Simulation of the effect of breakwater on the propagation of solitary waves., 24 (4): 780-789.

Verbrugghe, T., Domínguez, J. M., Crespo, A. J. C., Altomare, C., Stratigake, V., Troch, P.,, 2018. Coupling methodology for smoothed particle hydrodynamics modelling of non-linear wave-structure interactions., 138: 184-198.

Violeau, D., and Leroy, A., 2014. On the maximum time step in weakly compressible SPH., 256: 388-415.

Wang, X., So, R., and Xie, W. C., 2007. Features of flow-induced forces deduced from wavelet analysis., 23: 249-268.

Xiao, F., Honma, Y., and Kono, T., 2005. A simple algebraic interface capturing scheme using hyperbolic tangent function., 48 (9): 1023-1040.

Yabe, T., and Wang, P. Y., 1991. A universal solver for hyperbolic equations by cubic-polynomial interpolation I. One-dimensional solver., 66: 219-232.

Yabe, T., Tanaka, R., Nakamura, T., and Xiao, F., 2001. An exactly conservative semi-Lagrangian scheme (CIP-CSL) in one dimension., 129: 332-344.

Yang, Q., Jones, V., and McCue, L., 2012. Free-surface flow interactions with deformable structures using an SPH-FEM model., 55 (1): 136-147.

August 9, 2020;

November 12, 2020;

November 26, 2020

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2021

E-mail: jyp1220@163.com

E-mail: dongsh@ouc.edu.cn

(Edited by Xie Jun)