基于DBSCAN二次聚类的配电网负荷缺失数据修补

蔡文斌 程晓磊 王 鹏 王 渊

基于DBSCAN二次聚类的配电网负荷缺失数据修补

蔡文斌 程晓磊 王 鹏 王 渊

（内蒙古电力经济研究院，呼和浩特 010090）

电力负荷属于具有时间序列特性的数据，依据数据固有的规律性和波动性特征，修补由于各种因素而缺失的负荷数据，可为电力系统研究和实验结果的有效性和可预测性奠定基础。本文首先提出基于密度的含噪声应用空间聚类（DBSCAN）二次聚类的方法；其次，提出针对配电网负荷数据的负荷属性相似度，在此基础上进一步提出负荷记录综合相似度；然后，依据DBSCAN二次聚类方法的负荷类别结果和所得负荷记录综合相似度，匹配相似度最大的数据类别，并依据该类别的记录信息对所缺失数据进行修补；最后，采用算例分析证明所提方法的有效性和正确性。

基于密度的含噪声应用空间聚类（DBSCAN）；电力负荷；数据相似度；数据修补

0 引言

用电信息采集系统、自动化技术等在配电网的应用，为智能配电网运用大数据技术解决各种问题提供了路径。但是在电力数据的采集、传输及存储过程中常常会出现数据缺失、数据异常等质量问题，这些异常数据的存在使配电网的运行、调度、分析实验等工作受到潜在的影响。因此，如何对这些数据进行修复成为当前研究的一个重要热点问题。

事实上，针对缺失数据的处理技术广泛存在于各行各业之中，缺失数据处理工作随着各个领域特征的不同，以及数据应用目的的不同可采用多种方法[1]。实际处理时，往往根据缺失数据的特征属性、数据处理需要达到的目的、数据缺失的具体原因等选择最佳的处理方法以求达到最好的效果。配电网负荷数据往往存在时空特征明显、数据的规律性[2]较强、数据在电力系统规划、调度、运行等各个环节的应用面较广等特征，所以需要对缺失的数据进行较为精准的填充和修补。

针对配电网负荷数据具有时间规律的特点，对缺失数据的填充修补主要分为三种类型：①采用构造映射的方法，根据数据规律的相似性[3]，构造已有数据对缺失数据的映射[4]进行修补；②采用多重填补的方法，通过构造或者模拟影响其变动规律的相关因素的运动轨迹，推断出缺失数据的可能范围，再进一步通过统计、综合分析等方法从中优选最匹配结果[5]；③采用机器学习的方法，在海量数据集中进行数据集的聚类分析[6-7]，通过去噪、压缩感知等方法匹配与缺失数据所属数据集最为接近的特征，从而完成对缺失数据的填补。

在配电网负荷数据有较多积累的现状下，采用聚类分析，并按照特征匹配的方法填补缺失数据已成为针对具有时间特性规律数据的一种广泛而有效的方法。针对电力负荷数据，主要采用的聚类方法包括最近邻加权聚类[8-9]、K均值聚类[10-12]、熵权聚类[13-14]等多种分析方法，这些方法的基本思想均为先将数据对象聚类，划分成多个簇，根据簇内相似对象对缺失数据进行修补。其中，基于密度的含噪声应用空间聚类（density-based spatial clustering of applications with noise, DBSCAN）方法对数据集的分布不敏感，抗噪性好，且对于数据集的识别能力较强，针对空间分布较为广泛的配电网负荷数据聚类具有较好的适应性，但该方法在处理大量庞杂数据时的计算速度还有待进一步提高。文献[15]针对DBSCAN方法计算速度提升方面进行了深入的 研究。

基于上述背景，本文依据配电网负荷数据的时序特性，提出一种改进的DBSCAN二次聚类方法对配电网负荷缺失数据进行修补。首先依据负荷数据长周期特征的关键指标，提取每一个数据记录的关键信息，针对缩减的数据集进行初步聚类，然后在初步聚类的基础上针对完整数据再次进行DBSCAN空间密度二次聚类，以利于缩短由于庞大数据集而延长的聚类时间。其次通过负荷数据的数值属性相似度和记录值相似度比较，以相似度最大为原则、以同类数据属性相同为原则修复缺失的负荷数据。最后将仿真结果与实测数据进行对比，验证所提方法对配电网负荷数据修复的有效性和准确性。

1 DBSCAN配电网负荷数据聚类

1.1 DBSCAN聚类方法的改进

DBSCAN聚类方法在处理大量配电网负荷数据的过程中，分类器往往需要不断接触多种类型较新的未知实例，强大的填补算法会占用大量计算资源，造成计算速度下降的问题。故而，对聚类数据进行预处理，降低新数据的种类数，可以有效提高聚类算法的效率。

根据负荷数据同时具有短时间周期和长时间周期的多种周期性规律，提出先按照长时间周期对数据进行初步聚类，再在每一个类别内按照短时间周期再次聚类的方法，以提高聚类的速度。

负荷数据的长时间周期往往可以用较少的负荷信息表征，如表征负荷年内变化时，可以仅采用日（或周、月）的最大负荷或平均负荷等少量指标表征其变动趋势，这样压缩了负荷数据记录所包含的信息，每一条负荷记录仅包含长时间周期特征的少数几个数据，将在此基础上得到的初步聚类结果，称为负荷子集。然后在初步聚类结果的基础上，在每一个负荷子集内部按照短时间周期特性再对数据进行二次聚类，得到最终负荷分类。DBSCAN二次聚类示意图如图1所示。

图1 DBSCAN二次聚类示意图

由图1可见，每一个数据记录在整体聚类的过程中，均需要先提取长时间序列特征进行聚类，然后再次采用拥有完整信息的负荷数据进行二次聚类，即每一数据均经过了“双重”聚类。虽然总的聚类次数有所增加，但每一次聚类中涉及的数据量极大减少；且由于初次聚类已使长时间周期特征相同或相近的数据分布在同一数据子集内，二次聚类仅在子集内进行，使二次聚类时具有新特征的数据量极大降低，加之二次聚类可以实现多个数据子集并行聚类，故而极大降低了聚类计算需要的时间。

1.2 DBSCAN负荷数据二次聚类

DBSCAN是一种基于密度的聚类算法，其算法的基本假设是类别可以通过样本分布的紧密程度决定，即同一类别的样本，它们之间一定是紧密相连的，将紧密相连的样本划为一类，这样就得到了一个聚类类别。通过将各组紧密相连的样本划为各个不同的类别，则可形成聚类类别的最终结果。

因此，该方法有两个核心参数，分别为聚类半径（Eps）和样本个数阈值（MinPts）。聚类半径描述了某一样本的邻域距离阈值，而样本个数阈值描述了某一样本的距离为Eps的邻域中样本个数的阈值。两个参数综合起来反映了邻域的样本分布紧密程度。

算法根据所设置的聚类半径Eps和样本数目MinPts将待聚类数据分为核心点、边界点和噪声点3类，其中，在半径为Eps的圆内至少包含MinPts个样本的点称为核心点；在半径为Eps的圆内，样本数量少于MinPts个且落在核心点邻域内的点称为边界点；而既不是边界点又不是核心点的则被称为噪声点。

DBSCAN算法可以对任意形状的稠密数据集进行聚类，其聚类结果没有偏倚，并且可在聚类的同时发现异常点，对数据集中的异常点不敏感，同时具有较好的抗噪特性。

DBSCAN负荷数据二次聚类的主要思想为：首先将所有负荷数据集按照数据的完整性分成两个子数据集，即完整负荷数据集和缺失负荷数据集。完整负荷数据集保存了所有完整无缺失值的负荷数据。紧接着对完整数据集采用图1中所示的DBSCAN二次聚类方法，则完整数据集在进行了两次聚类后，得到若干个分类。

第一次聚类的目的是为了能够较快地将特征相似的数据聚类，故而在此过程中重点考察数据的关键特征，如表征数据水平的平均值、表征数据波动范围的最大值、最小值等少数特征。

通过第一次聚类后，已经将数据波动范围相同的数据聚为一类，则在此范围内，第二次聚类时重点可从负荷曲线的线形、时变特征等角度来进行二次聚类。

2 DBSCAN负荷数据聚类

相似度比较的基本思想都是在已有的完整数据分类中寻找与缺失对象属性最相似的对象来进行数据修补。电力负荷数据具有较强的时间规律，属于典型的数值型数据，且不具备离散数据的特点，故而根据负荷特性设定数值型属性，并以此属性衡量完整数据与缺失数据的相似程度。

2.1 负荷属性相似度

电力负荷的属性特性包含多种，基于其时间序列内连续的特点，一般表征负荷属性可用负荷最大值、最小值、平均值、负荷率、峰谷差率等多个指标进行描述。对于每一属性，均可以采用以下方法计算其属性相似度。

假设和是同一数据分类中的两条记录，其中x和y分别为表征两条记录针对属性的两个属性值，那么和对属性的属性值差异定义为

则和对于属性的相似度定义为

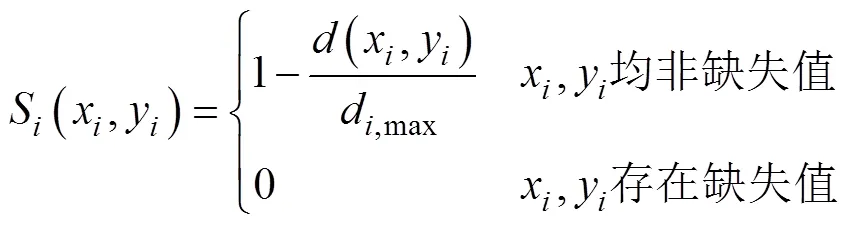
根据以上属性相似度的计算方法，可计算任意两条负荷记录针对某一属性（如负荷最大值、最小值、负荷率等）的属性相似度。

2.2 负荷记录综合相似度

由于表征时间序列负荷属性的指标为多个，因此有必要采用综合指标对多个属性相似度进行考量，即在计算了记录中的每一个属性相似度指标后，对多个属性相似度进行加权处理，比较重要的属性占有更大的权重，可以准确方便地比较数据集中任意两条记录的相似度。

针对同一个数据分类中的两条记录和，那么这两条记录对全部个属性的算数平均综合相似度为

考虑到负荷特征中各个属性的重要程度不同，故可对各属性相似度设置不同权重，比较重要的属性占有更大的权重，这样形成的综合相似度称为负荷记录综合相似度。带权重的负荷记录综合相似度表示为

负荷记录综合相似度用于判断具有缺失值的负荷记录与各个数据分类的相似度，以负荷记录综合相似度最大为原则，任选缺失负荷数据集中的一条记录逐一与这若干分类进行相似度比较，找到相似度最大的那个分类后，标记缺失值负荷记录为此分类中的一条记录，则该具有缺失值的负荷记录归并入负荷记录综合相似度最大的那一个类别，如此反复操作直至所有缺失值记录均并入某一分类类别，然后按照此分类的负荷属性值推算相应的缺失值，由此得到的缺失值具有较高的正确率。

3 算法流程

采用DBSCAN二次聚类算法对负荷数据缺失值进行修补的步骤如下：

1）将所有完整数据记录纳入数据集，将所有具有缺失数据的记录纳入数据集中。

2）提取数据集中的每一条记录的长时间周期特性值，如仅提取每一条记录中的最大负荷、平均负荷、最大负荷出现的具体时间等少数特征值形成新的记录，将所有新的负荷记录纳入数据集中。

3）确定参数Eps和MinPts，对数据集进行DBSCAN算法聚类，则按照参数设定数据集被划分为个数据子集，记为1,2, …,C。由于还需要进行二次聚类，所以参数MinPts可以设置得大一些，并据此调整Eps数值，以减少形成的子集个数。

4）对个数据子集，保留数据所属类别，恢复该类中每一记录的全部信息，对应得到个数据子集。

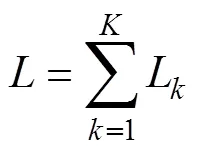
将得到的个数据分类记为1,2,3,…,C。

6）遍历数据集中的记录，逐一比较缺失值记录与这个数据类别的负荷记录综合相似度，取相似度最大的那个分类标记为缺失值记录所属类别。

7）上一步骤得到缺失值记录所属的分类类别，计算与该分类中其他完整记录中对应于缺失值属性的平均值，然后使用该属性平均值来修补记录的缺失值。

通过上面步骤6）和7），将中的每一条记录缺失值修补完毕，填充过的数据集记为'，数据集和数据集就构成了完整数据集。具体流程如图2所示。

图2 DBSCAN二次聚类数据修补算法流程

4 算例分析

选取2020年4月16日至6月15日某地区电网负荷数据，从本身不存在数据缺失的原始数据中随机选取占比10%的数据将其设置为缺失，则全月744个负荷中出现74个数据缺失，分别分布在5月份的13天里，其中连续缺失3个数据以上的情况为6个。则形成48条完整的日负荷记录和13条缺失值日负荷记录，采用文中所述DBSCAN二次聚类方法对此缺失数据集进行修补。

图3 DBSCAN二次聚类方法对缺失负荷曲线的修补结果

通过绝对误差和相对误差，可以进一步分析DBSCAN二次聚类数据修补的效果。

式中：为绝对误差，表示真值与修正值之间的数值差；%为相对误差，表示绝对误差占真值的百分比。

从图3可以看出，对缺失数据进行填补后的数据集，其数据的整体变化规律、趋势与原始数据基本吻合。缺失数据的填补值与真实数据之间的误差见表1，可以看出，采用DBSCAN二次聚类法对缺失值进行修补后，绝对误差平均值为31.223MW，相对误差平均值为1.85%，且误差基本可以控制在5%以内。同时，由图3可见，算法对连续缺失的数据修补效果也较好。

表1 修补结果误差

将以上修补结果与单纯DBSCAN聚类算法的负荷缺失值修补结果进行对比，分别对比其误差和计算速度，所得对比结果见表2。

表2 两种算法对比

由表2可见，相较于单纯采用DBSCAN聚类算法对缺失值进行修补，DBSCAN二次聚类算法修补结果的绝对误差最大降低了约24MW，相对误差平均值由2.32%降低至1.85%，起到了很好的修补效果。此外，从运行速度来看，采用DBSCAN二次聚类算法的计算耗时更短，也验证了该方法针对DBSCAN聚类方法速度的提升作用。

从实验结果来看，DBSCAN二次聚类针对普通的数据缺失修补效果非常好，总体平均误差在1%以内，主要原因是通过二次聚类形成的各数据类别中的数据，不但其数值大小较为匹配，数值的时变特征也非常接近，故而数据修补能够得到较好的效果。但是针对个别数据缺失出现在日负荷曲线极值处的情况，如图3中第22日和第10日的的峰值数据修补，由于这两日的峰值负荷点为较为陡峭的尖峰点，在二次聚类之后，与其处于同一类的其他负荷的尖峰不那么“突出”，且这两个数据所在类别中的尖峰时间有较小差异，所以在对尖峰值修补后出现了4.63%的误差。但是对于同类中尖峰的时间特征较为一致的其他数据分类，DBSCAN二次聚类修补算法仍然保持了2%以内的修补误差。

由于以上算例中数据记录数较少，仅采用了61条数据进行计算速度对比，若针对更大的数据量进行计算，则计算耗时将有更为显著的降低。

为了能够更进一步说明问题，将本文所提DBSCAN二次聚类方法与传统K均值聚类方法，以及当前较为常用的神经网络方法进行对比，对比的误差结果见表3。

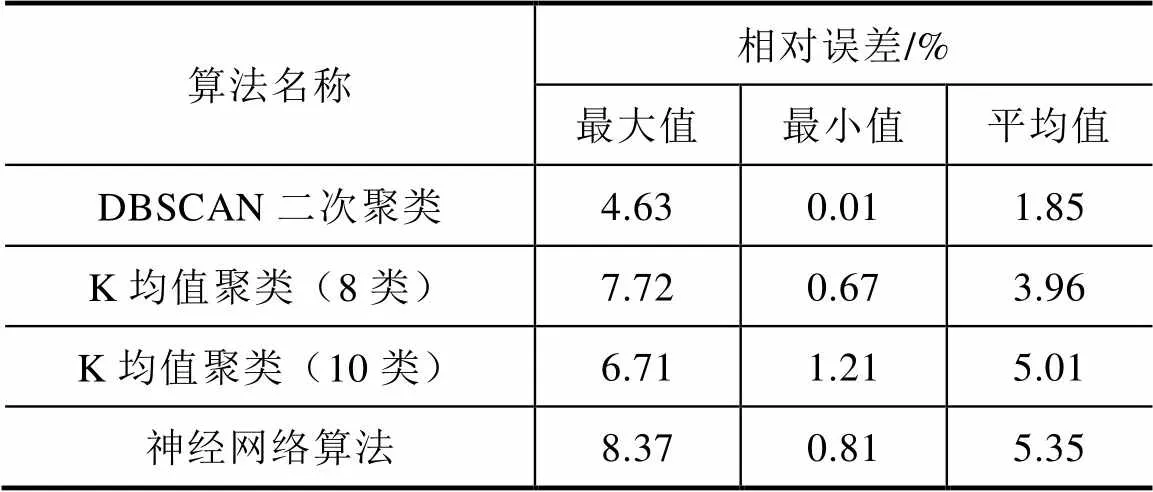
表3 DBSCAN二次聚类方法与K均值聚类及神经网络算法的修补结果对比

从表3可见，DBSCAN二次聚类算法的数据修补效果仍然最好。从方法原理上，对比DBSCAN聚类方法和K均值聚类方法的特点，DBSCAN方法在聚类的过程中，可以做到依据数据的密度进行数据分类，不必事先确定类别数量；而K均值聚类过程中，必须事先指定聚类的类别数量，且由于要将任一数值都归于某一类导致聚类结果对异常点比较敏感。故而DBSCAN聚类后，每一数据分类中数据的相似程度较高，这也是其能够有较高修复精度的重要原因。当然两类方法对比之下，K均值聚类方法有较快的计算速度，但采用DBSCAN二次聚类后，由于能够通过并行计算以提高计算速度，DBSCAN聚类方法的缺点已经得到克服。

由于神经网络算法需要大量的原始数据进行训练，所以在训练样本不足的条件下，神经网络算法的效果难以得到有效保证。在本例中，从具有一定数据规律的日负荷曲线角度而言，仅有48条完整负荷曲线，而对应的不完整负荷曲线则达到了13条，这也是导致神经网络算法的训练效果不够理想的主要原因；但是DBSCAN算法则不受此限制条件的严格制约，故而DBSCAN二次聚类算法能够得到较好的数据修复效果。

5 结论

针对配电网负荷缺失数据修补问题，本文研究得出如下结论：

1）在针对配电网负荷数据进行缺失数据修补时，DBSCAN二次聚类算法可以较好地依据负荷特性对负荷数据进行修补，且修补效果较好。

2）改进的DBSCAN二次聚类算法，通过首先按照长时间周期特征对数据进行初步聚类形成子集，再在每一个子集内按照短时间周期二次聚类的方法，有效提高了聚类算法的计算速度。

3）算例分析结果表明，DBSCAN二次聚类算法进行数据修补有更高的准确度，且针对连续性数据缺失也能取得较好的修补效果。

后续研究还需要重点结合两方面问题进行考虑：一是两次DBSCAN聚类中，参数Eps和MinPts大小的适度配合，尤其是面向更大量数据的时候，两者的相互配合直接关系到计算速度的提升幅度；二是负荷记录综合相似度包含多种负荷属性特征，针对不同类型的数据修补问题，各权重大小如何取值才能取得更好的数据修补效果。

[1] 熊中敏, 郭怀宇, 吴月欣. 缺失数据处理方法研究综述[J]. 计算机工程与应用, 2021(5): 1-13.

[2] 武佳卉, 邵振国, 杨少华, 等. 数据清洗在新能源功率预测中的研究综述和展望[J]. 电气技术, 2020, 21(11): 1-6.

[3] 王方雨, 刘文颖, 陈鑫鑫, 等. 基于“秩和”近似相等特性的同期线损异常数据辨识方法[J]. 电工技术学报, 2020, 35(11): 4771-4783.

[4] 王子馨, 胡俊杰, 刘宝柱. 基于长短期记忆网络的电力系统量测缺失数据恢复方法[J]. 电力建设, 2021, 42(5): 1-8.

[5] LITTLE R J A, RUBIN D B. Statistical analysis with missing data[M]. New York: John Wiley & Sons, 2019.

[6] 杨亚洲, 钱秋明, 梁鸭红. 基于k-means聚类方法的曲线按比伸缩置换缺失数据补全法[J]. 电气自动化, 2021, 43(2): 50-52.

[7] 胡金磊, 赖俊驹, 黎阳羊, 等. 基于自适应DBSCAN算法的开关柜绝缘状态评价方法[J]. 电工技术学报, 2021, 36(增刊1): 344-352.

[8] 杜沛, 程晓荣. 一种基于K近邻的比较密度峰值聚类算法[J]. 计算机工程与应用, 2019, 55(10): 161- 168.

[9] 陈曦, 骆高超, 曹杰, 等. 基于改进K-近邻算法的XLPE电缆气隙放电发展阶段识别[J]. 电工技术学报, 2020, 35(12): 5015-5024.

[10] 赵天辉, 王建学, 马龙涛, 等. 基于非参数回归分析的工业负荷异常值识别与修正方法[J]. 电力系统自动化, 2017, 41(18): 53-59.

[11] 林顺富, 谢潮, 李东东, 等. 基于灰色关联与模糊聚类分析的负荷预处理方法[J]. 电测与仪表, 2017, 54(11): 36-42.

[12] 翁秉钧, 杨耿杰, 高伟, 等. 一种基于改进K均值聚类的输电线路覆冰状态侦测方法[J]. 电气技术, 2021, 22(5): 43-49.

[13] 谢桦, 任超宇, 郭志星, 等. 基于聚类抽样的随机潮流计算[J]. 电工技术学报, 2020, 35(23): 4940-4948.

[14] 刘如辉, 黄炜平, 王凯, 等. 半监督约束集成的快速密度峰值聚类算法[J]. 浙江大学学报(工学版), 2018, 52(11): 2191-2200.

[15] 谢国伟, 钱雪忠, 周世兵. 基于非参数核密度估计的密度峰值聚类算法[J]. 计算机应用研究, 2018, 35(10): 82-85.

Repair of missing load data in distribution network based on DBSCAN secondary clustering

CAI Wenbin CHENG Xiaolei WANG Peng WANG Yuan

(Inner Mongolia Electric Power Institute of Economics and Technology, Hohhot 010090)

Distribution power load belongs to data with time series characteristics. According to the inherent regularity and fluctuation characteristics of the data, repairing the missing load data due to various factors can lay a foundation for the validity and predictability of the power system research and experimental results. Firstly, this paper proposes density-based spatial clustering of applications with noise (DBSCAN) secondary clustering method. Secondly, the load attribute similarity for distribution network load data is proposed, and the load record comprehensive similarity is further proposed. Thirdly, according to the load category results of DBSCAN secondary clustering method and the comprehensive similarity of the obtained load records, the data category with the largest similarity is matched, and the missing data is repaired. At last, the validity and correctness of the proposed method are proved by a numerical example.

density-based spatial clustering of applications with noise (DBSCAN); power load; data similarity; data repair

2021-06-15

2021-07-23

蔡文彬（1977—），男，内蒙古自治区呼和浩特市人，本科，主要从事配电网规划与运行管理工作。