基于3-D Gabor纹理特征和GBDT分类器的高光谱分类方法

杨志超, 赵 森

(1.浙江警察学院 刑事科学技术系，杭州 310053； 2.基于大数据架构的公安信息化应用公安部重点实验室，杭州 310053)

高光谱遥感图像(hyperspectral remote sensing image)是一种可以同时反映地物空间分布信息和光谱信息的3-D立体图像，在地物目标分类和识别方面优势巨大。随着传感器技术的发展，高光谱图像的光谱分辨率逐步提高。光谱分辨率提升，一方面增强了高光谱数据的可分性，另一方面，高维连续光谱数据中存在着大量的冗余信息，给后续的地物分类等高层分析带来了难度[1]。一般常用子空间投影的方法对原数据降维，比如主成分分析(principle component analysis，简称PCA)对高光谱数据降维后，再通过分类器识别地物目标[2]。A.Daamouche等[3]将小波变换的方法引入高光谱数据分类，并取得良好的分类效果。然而，高光谱分类的训练样本数一般较小，该方法只利用单像元的光谱维信息，对于图像空间维关系的利用不够充分，这是高光谱数据分类精度无法继续提升的重要原因。

D.Gabor[4]提出Gabor小波变换的方法，在信号分析中可以将时域和空域信息结合起来；而后，利用Gabor小波变换提取图像的Gabor特征，成功应用于提取纹理分类、人脸识别等领域[4-6]；Shi M. H.等[7]首次将Gabor小波分析引入高光谱图像分类领域，在空间维中逐个波段采用2-D Gabor滤波器提取分类特征；T.C.Bau等[8]在高光谱数据的光谱维和空间维应用3-D Gabor小波滤波器，取得良好的效果；Shen L.L.等[9]采用一系列不同频率和方向的小波滤波器提取空间维和光谱维及两者之间特征；冯逍等[10]利用Gabor特征结合支持向量机分类器，其准确率达到较高水平。这些工作表明，Gabor特征具有更高的可分性，能够获得更好的分类效果;同时，3-D Gabor应用于高光谱的立方体数据结构，提取的结果保留了纹理特征和光谱特征信息[11-12]。与Gabor特征一样，基于形态学的分析方法(extended morphological attribute profile, 简称EMAP)也可实现高光谱图像在波段和空间信息上的联合利用，并取得了较好的分类效果[13]。

另一方面，为了应对高光谱遥感图像数据的复杂变化和高维特性，近年来，核方法(如支持向量机)由于具有较好的鲁棒性，已成为高光谱图像分类的主要选择[14]。采用 Gabor滤波器提取纹理特征会加剧特征向量的高维特性[15]。而支持向量机等核方法本质上属于基于存储的方法(memory-based method)，随着训练样本和维数的增加，支持向量所需存储和在预测时的计算代价增加呈线性增长，导致分类效率和速度降低，时间加长[16]。近年，深度学习算法在各领域广泛应用，深度学习作为一种端到端的学习方法，节约了人工提取特征的过程。通过深信度网络提取空谱特征并完成高光谱数据分类取得较优的效果[17]。卷积神经网络(convolutional neural network, 简称CNN)作为深度学习算法的一种，在图像的特征提取和识别方面表现尤为突出，其在高光谱分类领域也取得比一般浅层算法更优异的表现[18-20]。

结合高光谱影像数据特点，本文提出利用梯度优化决策树对3-D Gabor小波变换的高光谱数据进行分类的方法。梯度优化决策树算法(gradient boosting decision tree, 简称GBDT)是一种将Boosting思想与决策树相结合的算法[21]，GBDT算法通过梯度优化方法训练多颗决策树，从而大幅度提升预测准确率。此外，梯度优化决策树并不需要存储训练样本，其本质上属于基于参数的模型(parametric-based method)，因而在预测时仍能具有较高的分类速度,特别是在数据维度较高或分类数据量较大时，更能体现其优势。

1 算法及原理

1.13-DGabor滤波器

3-D Gabor滤波器相比于2-D Gabor滤波器增加了一维光谱维，可定义为

G(x,y,b)=g(x,y,b)c(x,y,b)

(1)

式中：g(x,y,b)为Gabor滤波器的高斯核函数；c(x,y,b)为正弦部分。两部分函数的表达式分别为

(2)

c(x,y,b)=exp[jπ(xfx+yfy+bfb)]

(3)

其中：j∈N*(N*表示正整数集)；σ是高斯核函数的标准差，可根据式(4)得到，表示高斯包络在(x,y,b)空间中的宽度，其中b为正实数带宽，一般取1；fx,fy,fb分别表示中心频率f在x,y,b轴上的分量，如式(5)。

(4)

(5)

其中：θ是Gabor滤波器中心频率方向与x-y平面的夹角，φ是Gabor滤波器中心频率方向与b轴的夹角，其定义如图1所示。θ和φ共同确定了Gabor滤波器中心频率的方向。

图1 3-D Gabor滤波器的方向Fig.1 Directions of 3-D Gabor filter

1.2提取高光谱图像的纹理特征

3-D Gabor滤波器集合为Gfi,θj,φk(x,y,b)，高光谱图像数据立方体为HSI(x,y,b)，高光谱图像的纹理特征HSIt(x,y,b)是通过高光谱数据立方体与3-D Gabor滤波器进行卷积运算并取实部而得

HSIt(x,y,b)=

HSI(x,y,b)⊗Gfi, θj,φk(x,y,b)

(6)

其中：fi表示Gabor滤波器中心频率的振幅；(θj,φk)表示方向。fi,θj,φk的取值为

(7)

其中：I,J,K∈N(N表示自然数集)。在本文实验中，设置I=J=K=4，f的取值为[0.5, 0.25, 0.125, 0.0625]，θ和φ的值设置为[0, π/4, π/2, 3π/4]。当φk=0时，θj不论取何值，fi方向是相同的，因此本设置中Gabor滤波器共有4×4×3+4=52个。52个Gabor滤波器分别与高光谱数据立方体进行卷积运算后取实部，即可得到空间-光谱相结合的纹理特征。

1.3梯度优化决策树算法

梯度优化决策树算法(gradient boosting decision tree)是一种提升算法，是决策树算法与Boosting思想相结合的应用。GBDT的核心思想在于梯度优化，即训练时，每一棵树是从之前所有树的残差中来学习的。每一颗决策树Tm按照分枝增益最大的方式生长，回归树Tm的训练目标则是真实值与(T1+T2+T3+…+Tm-1)结果的残差，最终的预测结果是将所有树的结果相加得到。梯度优化决策树算法的主要步骤有：

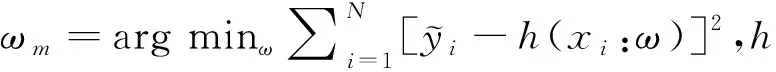
e.将当前树与已训练完成的树合并，Fm(x)=Fm-1(x)+γmh(x:ωm) 。

GBDT算法集成了多个决策树分类器，在训练模型时依次训练的，这个过程是线性的。但在预测分类时GBDT算法是并行计算的，预测效率较高。在数据维度较低时，GBDT算法的这个优势并不明显，但当数据维度升高或者数据规模增大时，其速度优势就凸显出来。

2 实验与结果分析

2.1实验设计

3-D Gabor特征的提取过程主要分为以下3步：(1)随机选择样本作为训练集，通过PCA降维算法剔除高光谱数据中的冗余信息，将原始高光谱数据降至50维。(2)利用52个不同方向和频率的3-D Gabor滤波器提取图像的纹理特征，获得的数据维度增加到2 600维(50×52)。(3)上述数据与原始高光谱数据合并成为总的分类特征，完成实验数据准备工作(图2)。

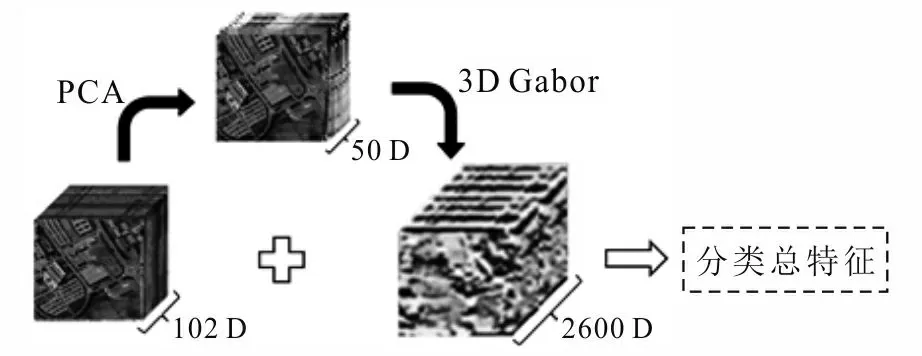
图2 实验数据准备流程图Fig.2 Flow chart for preparation of experimental data

2.2实验数据

实验选取Pavia University数据集和Indian Pines数据集进行实验。Pavia University 数据集为2002 年由Rosis传感器获取的高光谱图像，其大小为610×340像素，共115个波段，去除受噪声影响的波段，余下的103个波段用于实验。Pavia University数据集第50波段的高光谱图像和真实地物标记伪彩色图像如图3所示。Pavia University数据集包含 9类地物，地物类型与样本数目如表1所示。

表1 Pavia University数据集的地物类型与样本数目Table 1 Feature type and sample number of Pavia University data set

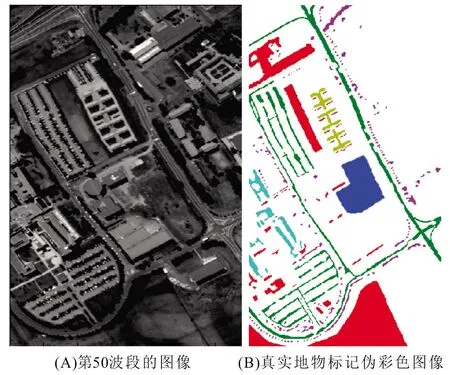
图3 Pavia University数据集Fig.3 Pavia University data set

Indian Pines是最早用于高光谱图像分类的测试数据，由机载可视红外成像光谱仪(AVIRIS)于1992 年对美国印第安纳州一块印度松树进行成像，然后截取145×145的大小进行标注作为高光谱图像分类测试用途。该光谱成像仪所成的图像的空间分辨率约为20 m，因此，其较容易产生混合像元，给分类带来难度。Indian Pines数据集第170波段的高光谱图像和真实地物标记伪彩色图像如图4所示。数据集包含16类地物，地物类型与样本数目如表2所示。

表2 Indian Pines数据集的地物类型与样本数目Table 2 Feature type and sample number of Indian Pines

图4 Indian Pines数据集Fig.4 Indian Pines data set

2.3实验环境

计算机环境为CPU：Intel(R)Core(TM)i5-5200U@2.2 GHz, RAM：12.0 GB, 64位Windows操作系统。

2.4结果与讨论

在Pavia University数据集和Indian Pines数据集上对Gabor+GBDT, Gabor+SVM, 3-D Gabor+SVM, 3-D Gabor+GBDT, CNN, EMAP+SVM进行分类实验。实验的目的有两方面，一方面通过与Gabor特征、EMAP特征的对比，检验3-D Gabor特征的有效性；另一方面，通过与SVM和CNN的对比，检验GDBT分类器的分类准确率和分类效率。

SVM算法有2个重要参数：惩罚系数和影响范围，通过网格实验得到最优的惩罚系数=10，影响范围=0.01；实验中Gabor特征为空间二维Gabor特征，其参数设置如文献[7]。 GBDT算法中树的最大深度max_depth=10；实验中CNN采用3×3×3的三维卷积分类模型，网络结构如文献[19]。随机抽取样本数据的5%～50%(步进为5%)作为训练样本，剩余做分类样本。利用训练时间、分类时间、准确率进行表征，以此评价各方法的分类效果，重复10次实验，取统计平均值作为最终实验结果。

如图5所示，3-D Gabor+SVM和3-D Gabor+GBDT的准确率明显高于其他方法，证明3-D Gabor小波得到的纹理特征对提高分类准确率有显著的帮助。在两个数据集上，SVM算法的准确率都是最高的，GBDT算法稍低于SVM算法。CNN算法的准确率低于前两种算法，特别是在Pavia University数据集中。使用简单Gabor特征和EMAP特征的准确率明显低于3-D Gabor特征，说明3-D Gabor变换对于提取高光谱数据的纹理特征非常有效，可以大幅度提高准确率。

图5 6种算法的准确率比较Fig.5 Comparison of accuracy of six algorithms

分类算法的训练时间如图6所示。Gabor+GBDT, Gabor+SVM, 3-D Gabor+SVM,EMAP+SVM四种算法的训练时间消耗明显较少。3-D Gabor+GBDT和CNN算法训练时间更长，随训练集的增大，训练时间也逐步增长。两者相比，3-D Gabor+GBDT方法相比CNN算法训练用时更少。

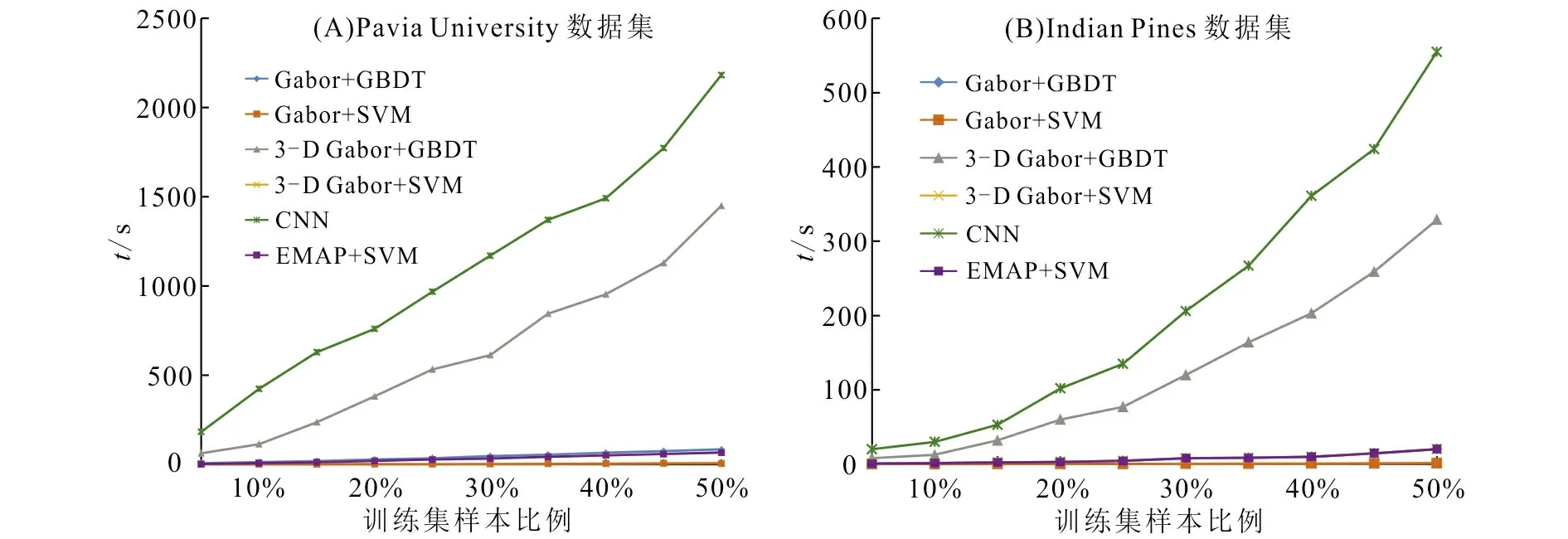
图6 6种算法的训练时间比较Fig.6 Comparison of training time of six algorithms

在分类时间上的比较结果如图7所示，Gabor+SVM和3-D Gabor+SVM的分类时间最长，主要是因为SVM算法复杂度是O(M2N)，其中N为样本数，M为特征维数，当特征维度增加时，其计算消耗的时间大幅度提高。相对而言，CNN和GBDT算法的分类速度快很多，其中GBDT算法的分类效率更高，用时最少。

图7 6种算法的分类时间比较Fig.7 Classification time comparison of six algorithms

3 结 论

本文分别从准确率、训练时间和分类时间3个方面比较了多种算法的高光谱图像分类效果。在实验的两个数据集中，3-D Gabor+GBDT方法的优点非常显著。(1)3-D Gabor+GBDT方法的分类准确率较高，明显高于CNN算法、Gabor以及EMAP为纹理特征的方法。(2)3-D Gabor+GBDT方法分类效率高于CNN和以SVM为分类器的方法。(3)3-D Gabor+GBDT的劣势，主要在其训练时间较长，建模效率偏低。

因此，3-D Gabor+GBDT方法特别适合在线分类的场景，此类场景需要较高的分类效率和准确率，但对前期训练建模的时间敏感度低。