无人驾驶汽车转向系统参数自整定及优化研究
张中原,张幽彤
(北京理工大学 机械与车辆学院,北京 100081)
无人驾驶作为汽车领域的主流研究方向,高速复杂工况下的汽车转向亟待解决,而转向执行机构的控制性能作为关键需要学者进行研究攻关[1]。永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)由于具有效率高、节能环保、高效能、结构类型多样等优点,广泛应用于机器人、数控加工、汽车、航空航天等领域[2]。目前,PMSM 伺服系统大都采用三闭环PID 级联的矢量控制方式,而PID 控制参数的整定对系统的控制性能起到决定性的作用[3]。
近年来国内外学者在PID 参数自整定建模及策略方面做了许多工作。FREIRE 等[4]通过试验验证了适用于非线性系统的自适应神经元PID 控制器(AN-PID)。YADAV 等[5]提出了自适应神经模糊推理系统(Adaptive Neural Fuzzy Inference System,ANFIS),解决了固有的非线性问题。BOILEAU 等[6]利用卡尔曼滤波器辨识电机角速度及磁链实现了无位置传感器控制。JUNG 等[7]提出了一种新型自适应PID 控制器,由解耦项、PID 项和监控项组成,分别补偿非线性因素、自动调节控制增益和保证系统稳定性。贺云波等[8]提出通过RBF 神经网络在线辨识,结合现在流行的学习算法进行位置环PID 参数自整定。陈天等[9]根据相角裕度、频率响应等参数,通过使系统稳定计算出速度环PID 参数。左月飞[10]简化了系统模型后,基于状态方程设计了复合PI 控制器。蒋捷等[11]提出改进的差分进化算法,选取误差绝对值与时间乘积的平方项作为目标函数,同时引入惩罚项抑制超调量。
传统PID 参数的整定往往通过人工试凑的方法得出,导致PID 出厂参数固定,无法随着系统负载工况的变化而变化,进而影响系统在不同工况下的超调量和响应速度[12]。针对传统人工试凑法改进的PID 整定技术可分为基于模型和基于规则的参数整定[13],基于模型方法整定PID 参数用时短,但控制效果不够理想,基于规则方法整定PID 控制效果显著,但计算时间较长[14]。
为了满足无人驾驶高速复杂工况转向机构的控制要求,本文提出一种综合模型和规则的参数自整定方法。首先,设计三闭环各环为典型I、II 型系统求取PID 初值;其次,用模型参考自适应算法对PMSM 转动惯量辨识;最后,结合目标函数和共轭梯度法在初值邻域求取最优PID 参数。
1 PMSM 伺服系统控制结构
本研究所用的PMSM 伺服控制系统结构在传统三闭环基础上进行改进,如图1 所示。

图1 id=0 的PMSM 伺服系统控制系统结构
首先,建立合适的PMSM 数学模型,考虑到PMSM 是一个非线性、强耦合的复杂对象,为了简化分析,需要作出如下假设[15]:(1)忽略磁路饱和、涡流和磁滞损耗。(2)定子绕组空间中每两相相差120°,感应电动势是正弦的。(3)永磁体无摩擦力作用,无电导率。
电机的电压方程在dq轴旋转坐标系下为:



式中:TL为负载转矩;B为粘性阻尼系数,本文中由于假设电机没有阻尼力,因此B=0;J为转动惯量;ωn为电角速度。
在图1 中,位置环控制器为P 控制器,速度环与电流环控制器均为PI 控制器,传递函数分别为:

2 PI 参数自整定策略
2.1 基于典型系统的参数整定
2.1.1 速度环参数整定
电流环是PMSM 伺服系统最内环,由于电流环的参数整定可由电机电气参数、采样方式和逆变器决定[16],与转动惯量无关,较为简单,本文将其推导详细过程省略。
由图1 可知,将速度环单独剖析出来,包括速度PI控制器、电流控制闭环、编码器、PMSM和负载。电流闭环传递函数可以设计为典型I 型系统,由于电流环响应速度比速度环快10 倍左右,所以电流闭环传递函数可近似为:

进而得到速度环数学模型,如图2 所示。

图2 速度环数学模型

式中:未知量转动惯量J为电机与负载转动惯量之和,因此需要对系统参数进行在线辨识。
2.1.2 位置环参数整定
对位置环进行参数整定时,速度环处于内环可作为一阶惯性环节处理,因此简化为:
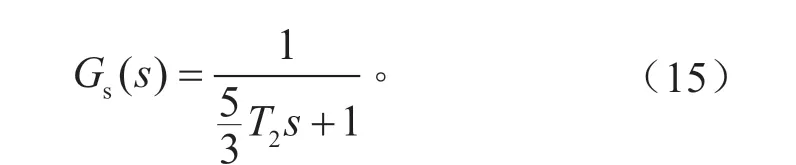
根据图1,将位置环单独剖析出来,位置控制器为纯P 控制器,同时要加入1 个位置前馈,以改善系统的超调量和响应速度。带前馈位置闭环数学模型如图3 所示。
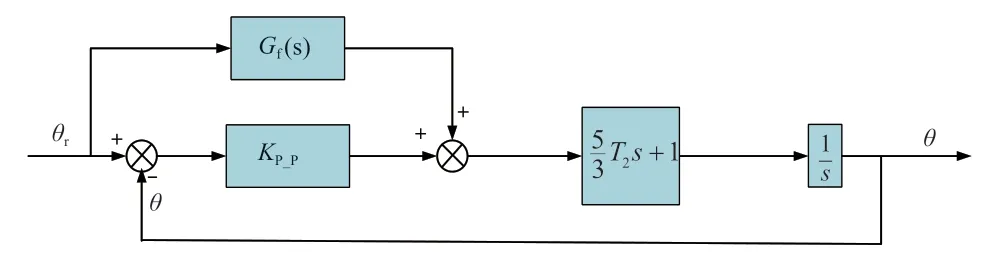
图3 带前馈位置环数学模型
图中,Gf(s)为前馈控制器。由图3 可推出误差传递函数为:
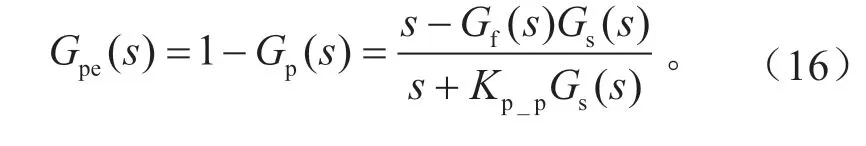
要使系统实现无误差跟踪,则误差传递函数应为0,可推出前馈传递函数为:
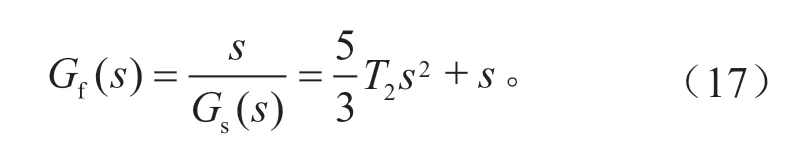
式(17)由速度前馈项和加速度前馈项构成,工程应用中采用速度前馈即可满足控制需求,于是前馈传递函数简化为:


2.2 转动惯量辨识
由于速度环PI 参数整定需要进行转动惯量在线辨识,本文提出利用模型参考自适应算法对电机及负载的转动惯量进行识别。自适应律根据两个模型输出误差调节可调模型中相应的参数,如果算法收敛,最终参考模型和可调模型有相同的输入输出,可调模型的参数值就是参考模型对应参数的辨识值[17]。
对于PMSM,参考模型是电机的机械特性,转动惯量是要识别的参数。电机机械特性运动方程如式(6)所示。将其离散化可得:


图4 转动惯量在线辨识结构
2.3 共轭梯度法优化
上文利用模型推导出电机三闭环的PI 参数,其随着电机的负载变化而变化,但基于单一性能指标所得到的参数并不能全面反映系统的动态性能,因此需要提出一个基于多项性能指标的评价指标函数,将上文所得参数作为初值,利用共轭梯度法在其邻域内进行寻优,使电机的稳定性和快速性达到最佳平衡态。
在三闭环的控制中,由传递函数时域特性可知,最优的PI 参数会尽量缩短上升时间和调整时间,减小超调量,所以设计评价指标函数为:

式中:Kp,Ti为待优化参数,分别为比例系数和积分时间;tr为上升时间,取系统输出第1 次达到目标值的90%的时间为准;ts为调整时间,为系统输出首次稳定在目标值的±统输范围以内的时间;e(t)为系统输出达到目标值后的输出偏差;ω1,ω2,ω3为权重因子,可以通过调节加权系数的大小,调节评价指标函数各项的比重,实现评价指标对不同相应性能的着重描述。显然,评价指标函数的值越小,说明系统的响应性能越好。
寻优问题有很多高级算法。例如:遗传算法,最小二乘法等,但其计算复杂,不适用于本研究只寻求两个参数的最优解,因此采用共轭梯度法,仅需利用一阶导数信息,就可以快速寻优,既保证了收敛速度快,又解决了大量数据的存储问题。
共轭梯度法的具体步骤如下:

(5)由式(27)确定d(k-1),令k=k+1,转到第2 步继续迭代。
3 仿真与试验验证
3.1 Simulink 仿真
根据上文理论推导,在Matlab/Simulink 中搭建PMSM 伺服系统三闭环控制模型如图5 所示,主要包括PMSM、CLACK 变换、PARK 变换、反CLACK 变换、SVPWM、转动变量辨识以及各环控制器。图中电机的仿真参数见表1。

表1 仿真电机参数
如图5 所示,根据式(14)和式(20)整定初始PI 参数见表2。

图5 PMSM 伺服系统Simulink 模型

表2 初始PI 参数
然后采用共轭梯度法在初始PI 参数邻域进行控制参数寻优,共轭梯度法寻优算法在.m 文件中编写,评价指标函数中权重系数分别取ω1=10 000,ω2=1 000,ω3=0.001。
三闭环调试要由内向外,首先调节电流环,设计目标电流为2 A,设定仿真时间0.05 s,针对电流环优化,在共轭梯度法寻优算法中,PI 参数最终确定见表3。
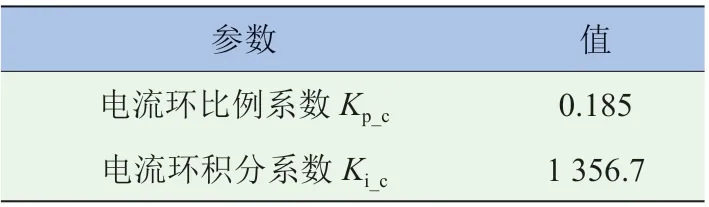
表3 电流环优化PI 参数
两组PI 参数可得到优化前后的电流响应曲线对比,如图6 所示。由图中曲线最大值坐标点可知,超调量优化前为0.696 A,优化后为0.243 A,则优化后超调量较优化前降低了16.8%;上升时间有所缩短;评价指标函数值由优化前的6.532 2 降低为3.939 3。评价指标函数值的降低证明了优化后的PI参数有更好的系统响应,是平衡了超调量、上升时间和调整时间的综合最佳PI 参数。

图6 电流环响应曲线对比
而后调节速度环,将电流环PI 参数设定为优化后PI 参数,设计目标转速200 r/min,设定仿真时间0.05 s,针对速度环进行优化,在共轭梯度算法中优化最终PI 参数,见表4。

表4 速度环优化PI 参数
两组PI 参数可以得到优化前后的速度环响应曲线对比,如图7 所示。由图可知,优化前速度环响应曲线没有超调,优化后超调量为5 r/min,则优化后超调量较优化前上升了2.5%;上升时间优化前为0.000 748 s,优化后为0.000 17 s,则上升时间大幅度降低,下降了77.27%;评价指标函数值由初始的41.52 下降到优化后的17.38。尽管超调量上升而上升时间降低无法很好地判断优化效果,但通过评价指标函数值可以很简单地看出上升时间,调整时间的降低程度对系统响应的影响远大于超调量的上升程度,因此,优化后的PI 参数同样为最佳PI 参数。
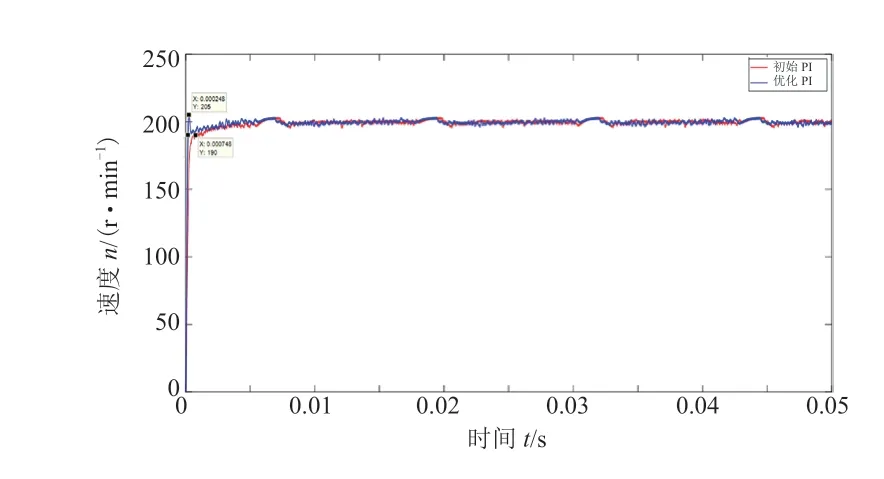
图7 速度环响应曲线对比
最后调节位置环,先将内部两环PI 参数设定为优化好的参数,而后设计目标位置2πrad,设定仿真时间0.2 s,同时将评价指标函数中权重系数改为ω1=ω2=100,ω3=0.001,负载设为0,优化位置控制器P 参数见表5.

表5 位置环优化P 参数
两组PI 参数可以得到优化前后的位置环空载响应曲线对比,如图8 所示。由图可知,优化前没有超调,优化后超调量为0.195 rad,则优化后超调量较优化前上升了3.10%;上升时间优化前为0.069 s,优化后为0.054 93 s,则上升时间大幅度降低,下降了20.39%,同时评价指标函数值由初始的20.705 5下降到优化后的12.306 3。位置环优化效果与速度环相近,尽管超调量有所上升,但不及上升时间与调整时间的下降程度,因此,优化后的PI 参数仍为最佳PI 参数。
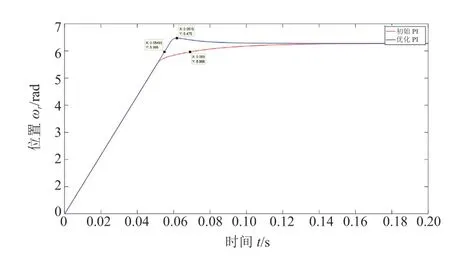
图8 位置环空载响应曲线对比
最后将负载设为0.28 Nm,优化前的各项系数设定为位置环空载优化后的PI 参数,其他仿真环境不变,经共轭梯度法优化,得到优化后的PI参数,见表6。

表6 带负载优化PI 参数
分别仿真得到带负载条件下优化前后的位置环响应曲线对比,如图9 所示。由图可知,优化前无超调量,优化后超调量为0.059 rad,则优化后超调量较优化前上升了0.94%;上升时间优化前为0.037 63 s,优化后为0.021 77 s,则上升时间大幅度降低,下降了42.15%,同时评价指标函数值由初始的11.444 下降到优化后的4.867 7。可以得到类似的结论,即优化后的PI 参数为最佳PI 参数,同时证明了固定的PI参数无法适应变负载工况,而共轭梯度法的实时优化PI 参数可以满足负载变化的工况。

图9 位置环负载响应曲线对比
综上所述,经过“电流环-速度环-位置环”的分别仿真,可以在仿真的层面验证本文参数自整定算法的有效性,下面将进行试验验证。
3.2 试验验证
上文通过理论推导、仿真分析验证了本研究算法的有效性,为了进一步证明其可靠性,针对本文所述PMSM搭建单人车作为试验平台,如图10所示,详细参数见表7。

表7 试验平台参数

图10 试验平台
用本文所述PMSM 取代传统转向助力电机,通过速比为10 的减速器进行转向传动。控制器为控制板+驱动板结合而成,控制板选用TI 公司的TMS320F28335 作为主芯片,驱动板选用IR2136 作为MOSFET 驱动芯片,电机通过2 500 线增量式编码器进行位置、速度和电流反馈。
针对位置环进行实车测试,首先进行空载试验,与空载仿真环境设置一致,可得到如图11 所示的位置环空载试验响应对比。由图可知,优化前无超调量,优化后超调量为0.2 rad,则优化后超调量上升了3.18%;上升时间优化前为0.069 31 s,优化后为0.053 46 s,则上升时间下降了22.87%。由于超调量上升和上升时间下降程度与空载仿真基本相似,可以证明优化后PI 参数为最佳PI 参数。

图11 位置环空载试验响应对比
最后进行负载试验,同样与负载仿真环境设置一致,可得到如图12 所示的位置环负载试验响应对比。由图可知,优化前无超调量,优化后超调量为0.175 rad,则优化后超调量为2.8%;上升时间优化前为0.036 s,优化后为0.018 s,则上升时间下降了50%。同样根据负载仿真数据指导,可以证明优化后的PI 参数为最佳PI 参数。
通过对比图8、图9、图11 和图12,可从试验层面验证以下两个结论:
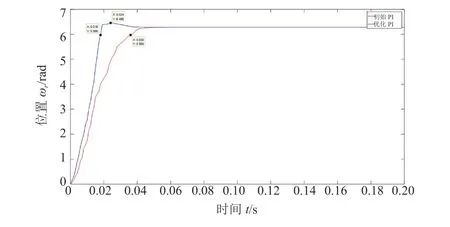
图12 位置环负载试验响应曲线对比
(1)固定PI 参数无法适应PMSM 变负载工况,一旦负载变化,会导致超调量和响应速度的变化,无法做到快速准确的位置响应。
(2)本文提出的综合PI 参数自整定算法可以快速、准确地调整PMSM 的PI 参数,从而适应无人驾驶的各种驾驶工况。
4 结论
(1)针对高速复杂工况下的无人驾驶汽车转向,对PMSM 伺服系统进行了PID 参数自整定控制策略研究。提出了一种模型与规则相结合的新型PID 参数自整定控制策略,较单纯的模型PID 参数自整定更为精确,较单纯的规则PID 参数自整定更为快速。
(2)本文所述的控制策略采用模型参考自适应算法进行PMSM 转动惯量辨识,利用典型系统整定三闭环PI 初值,再利用共轭梯度法在初值邻域寻优。对优化前后的PI 参数进行仿真试验对比发现,利用共轭梯度法优化的PI 参数有更快的响应速度,超调量上升不大,基本在5%以内,上升时间下降20%~50%。通过对比空载和负载的PI 参数曲线响应,可以看出PI 参数自整定策略可以使控制器跟随负载工况实时变化,以满足无人驾驶汽车转向的各种工况,如原地起步转向、车道保持、紧急避让等。

