考虑用户偏好和平台收益的共享泊位分配模型

任军效，常 新，侯 滢，曹小博

1.西安电子科技大学 人文学院，西安710071

2.西安交通大学 人文与社会科学学院，西安710049

城市中的泊车问题一直是让用户烦恼的问题。一方面，机动车的增长速度远远超过了泊位的增长速度，新建泊位已经满足不了需求，用户面临“泊车难”的问题；另一方面，泊位使用不均衡，部分住宅区的泊车场白天有空位，夜间则占有率较高，而办公楼的泊车场则恰恰相反，白天占有率高而夜间有空闲泊位。这使得泊位共享有条件实施。《中共中央 国务院关于进一步加强城市规划建设管理工作的若干意见》指出“合理配置泊车设施”“推动社区内公共设施向居民开放”。这一意见为泊位共享提供了政策支持，为了解决“泊车难”的问题，现有泊车场需要开放，实现私人泊位共享，或者物业公司将空闲的泊位移交给平台，平台通过优化分配以实现用户共享，泊位共享将减少道路拥堵，减少车辆巡航过程中排放的有害气体，减轻节能减排的压力。

用户泊车选择的影响因素有：泊车费、步行距离、非理性因素等。丁浣等[1]建立了路内巡航泊车行为模型，发现泊车费可以调节巡航时间，对用户选择有影响作用。在泊车定价对用户选择的影响方面，Liu等[2]认为动态定价可以减轻用户随机性造成的收入损失；Kim等[3]分析了动态定价下预约方案的有效性，可用于泊位共享；Guo等[4]提出决策的非理性成分（乐观或悲观）对泊车行为有显著影响，利用动态模型对泊车行为建模和预测。肖海燕等[5]提出政府对公交车的激励效应以及对私家车管制效应对用户出行方式选择有重要影响。

基于平台视角，城市泊位分配策略主要有：平台运营商利润最大策略、拍卖分配策略、社会福利最大策略等。李涛等[6]假设流率服从正态分布，建立了泊位分配优化模型。姚恩建等[7]利用有向图论分析了居住区共享泊位分配模型，提高了泊位占有率。孙智慧等[8]以提高泊位共享利用率和用户满意度为目标，将预订用户按照偏好顺序依次与泊位进行匹配，泊位利用率最大的用户为匹配成功的用户。孙会君等[9]以泊位共享平台运营商利润最大化为目标，提出泊位分配的整数规划模型，有效提高运营商的利润与泊位周转率。另外，Myerson[10]提出的最优拍卖设计可应用于泊位分配，张骥先[11]、刘旭东[12]等提出一种基于拍卖的资源分配算法，采用基于最小费用最大流算法，实现社会福利最大的目标。林小围等[13]将合作博弈应用于泊位分配，降低了用户的泊车成本。Ottosson[14]、PU[15]等评估泊车场占用率对泊车价格变化的敏感性，对共享泊车定价有借鉴意义；旧金山、西雅图和华盛顿特区根据时间调整路边停车的价格，基于占用率调整价格的策略可以提高路内停车和相邻道路的性能[16]。Wang等[17]根据出行者的选择偏好构建了泊车许可证的最优分配-定价模型，对泊车许可证进行拍卖，利用Shapley value法构建基于对社会福利贡献程度的泊车收益分配模型。He等[18]讨论了将泊车竞争引导到泊车位均衡分配的最优定价方案，引入一个有效的价格向量，确保泊车竞争结果保持系统最优。

当前的研究详细分析了用户选择的影响因素、平台分配的优化策略和分配优化模型。但在考虑平台泊位分配的收益时，忽略了用户泊车的选择偏好，在考虑用户满意度时没有考虑偏好顺序。案例将用户的选择偏好与平台收益结合起来，按用户的偏好顺序分配，实现了平台收益。

1 基础知识

泊位不同于一般的资源，使用时间不同，报价也可能不同。比如，即使去同一个目的地，有的用户喜欢将车停在目的地，有的用户喜欢将车停在距离目的地较远的泊车场，然后步行前往目的地。这导致了不同的泊车成本。泊车成本包括寻泊成本和泊车费，当不考虑道路情况和步行距离时，用户泊车选择主要考虑寻泊时间、出行成本等。采用累积前景理论构建用户的泊车选择模型，平台采用偏好分组法分配。

1.1 用户选择的影响因素

期望效用理论描述了“理性人”在风险条件下的决策行为。用户在决策时，对于选择的后果不确定，具有一定的风险。有的用户注重泊车费，有的用户注重巡航时间，当选择的结果与概率都明确的情况下，用户会直接选择，但多数情况下结果是不明确的。用户的泊车选择主要考虑以下因素：泊车费、步行距离、寻泊成本和非理性因素。泊车费即泊车场收取的预定费用和占用期间的费用。步行距离即用户泊车后步行至目的地的距离。寻泊成本主要是指巡航时间以及巡航过程中产生的燃油费、拥堵费及车辆磨损等。非理性因素指的是用户的情感、意志等，如泊车时的乐观、悲观等情绪。

1.2 影响因素的评价

假设不考虑步行距离与非理性因素，只考虑寻泊成本和泊车费，每个泊车场的泊车费是明确的，用户采用累积前景理论来确定寻泊成本的大小。

用户根据参照点，判断寻找泊位过程中的各影响因素的价值。刘玉印[19]、田丽君[20]等采用累积前景理论构建出行者的出行方式选择模型，计算了出行成本。累积前景理论主要包括价值函数和累积概率权重函数。当结果相对于参考点为收益时，人们是风险厌恶者；当结果相对于参考点为损失时，人们是风险寻求者。假设用户早上去城市的CBD办事，CBD地下室有配套车位，但早高峰期间常常没有空闲泊位，需要等待。CBD附近有私人共享泊位，较远处也有公共共享泊位，三种情景可供用户选择。假设用户泊车分别考虑收益和损失的价值函数为：

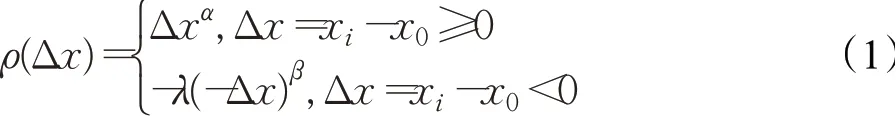
采用Tversky和Kahneman[21]提出的累积概率权重函数，当用户面临“收益”时，主观感知概率加权函数为：

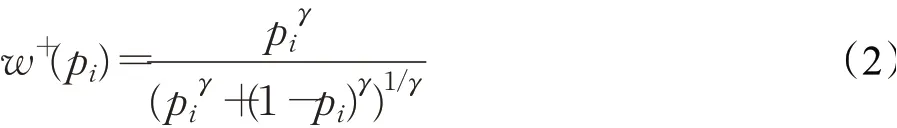
当用户面临“损失”时，主观感知概率加权函数为：

累积决策权重为：

累积决策权重为：

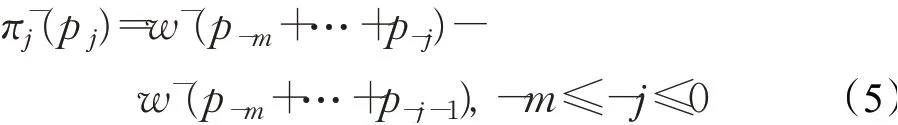
用户泊车的累积前景值可表示为：

其中，α、β表示衡量远离参考点的敏感性递减程度。α、β越大表示出行者对风险越敏感，λ表示损失规避系数，γ和δ决定权重函数的曲率，根据实验数据，一般取α=0.88,β=0.88,λ=2.25,γ=0.61,δ=0.69。

1.3 偏好分组

用户在网上进行竞价，搜索泊车信息，将报价提交到平台。平台通过给泊车位的位置编号，设置不同的使用时间段及竞价，以最大化泊车位利用率，获取最大收益。平台先将某一泊位第一偏好的报价由高到低进行排序，只要满足匹配的条件，就通知用户，若用户未满足第一偏好，平台会分配一个第二偏好的泊车位，若用户同意就会接收，否则平台会分配一个第三偏好的泊车位。以此类推。用户报价应高于平台所规定的最低价，当两个用户报价相同时，遵循“先到先服务”的原则。平台分配时既考虑了平台的收益，又考虑用户的偏好。考虑泊车位最大利用率，尽可能缩短两个用户的使用时间差。没有成功泊车的用户不需要支付。

2 用户选择和平台分配的优化模型

2.1 用户选择模型

对于不同类型的泊位，如果用户只有一种选择或只需提交一个竞价，可能无法完成用户满意的分配。现实中用户根据自己的感知寻泊成本，可能对多种类型的泊位有偏好顺序，让用户对多种泊位分别报价，平台分配时就有参考依据。

用户出行成本包括寻泊成本和泊车费，用户的寻泊成本包括巡航时间，早到延误成本或迟到延误成本等，函数定义如下：

其中，Ccruise=θcruiseTcruise表示巡航时间成本，Cearly=σθearly(Tw-Tfind)表示早到延误成本，Clate=(1-σ)θlate(Tfind-Tw)表示迟到的延误成本，θcruise、θearly、θlate分别表示对应的单位时间巡航成本、单位时间早到成本和单位时间迟到成本，且满足θearly＜θcruise＜θlate，Tcruise是用户实际的巡航时间，Tarrival表示用户到达目的地的时刻，Tfind表示用户找到泊位的时间，Tfind=Tarrival+Tcruise，Tw表示必须到达的时间，σ为0-1变量，满足如下：

由于用户并不能准确地知道实际的寻泊时间，只能估计出选择某一泊车方式的主观感知时间Tperceived，则感知泊车成本Cperceived为：

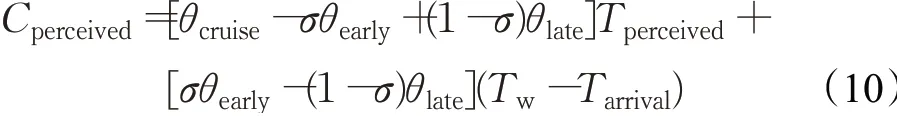
下面通过一个例子来说明用户的选择过程：

假设用户去CBD上班，泊车3 h，CBD地下室的配套车位的泊车费为0.5元/15min，私人共享泊车场就在CBD附近，泊车费为1元/15min，公共共享泊车场较远，泊车费为0.8元/15min，泊车时间相同，成本中没有考虑道路情况、步行距离的影响。分三种偏好情形进行分析，即选择CBD配套泊位、选择私人共享泊位、选择公共共享泊位。以上班时间为界，到达目的地的时间为Tarrival，找到泊位的时刻为Tfind，三种偏好情形下的感知寻泊时间Tperceived如下：

情形1在CBD配套泊位排队泊车，需要等待10 min，泊车费为0.5元/15min。

情形2共享私人泊位，泊车费1元/15min，寻泊时间有20%的概率为12 min，80%的概率为5 min。

情形3共享公共泊位，泊车费0.8元/15min，寻泊时间有40%的概率为15 min，60%的概率为10 min。

根据用户到达目的地的时间不同，用户的泊车方式不同，假定场景如下：

假定场景 到达CBD后，必须在10 min内找到泊位，预算泊车时间为Tbudget=Tw-Tarrival=10 min。

按照累积前景理论，用户通过感知到的累积前景值来选择泊车方式，由用户的预算出行时间计算出预算出行成本Cbudget如下：

选择Cbudget作为用户泊车方式的参考点，Cperceived＞Cbudget，用户感知到“损失”；Cperceived＜Cbudget，用户感知到“收益”。假设时间成本（单位：元/min）θcruse=1，θearly=0，θlate=1.5，Tw=9:00。

在假定场景，到达CBD的时刻为Tarrival=8:50，Tbudget=10，代入式（10），得到感知泊车成本。

因此，假定场景下三种泊车方式的感知出行成本如表1所示。

表1 假定场景下三种泊车方式的感知泊车成本Table 1 Perceived parking costs of three parking modes under hypothetical scenarios

将感知泊车成本与假定场景下Cbudget=θcruiseTbudget比较，可得三种泊车方式的累计前景值（CPV）如表2。

表2 假定场景下泊车方式的CPV值Table 2 CPV values of parking mode under hypothetical scenario

假定场景中，用户必须在10 min内找到泊位，在累积前景理论框架下，共享私人泊位时有迟到的风险，用户更愿意冒险以节省时间，其寻泊成本优于其他两种方式，是最优方案。如果偏好无法得到满足，则选择非共享泊位为第二偏好，如果第二偏好无法得到满足，则选择共享公共泊位为第三偏好。用户的泊车偏好是根据自身感知的累积前景值来确定，接下来，假设用户泊车可以选择偏好，用户根据自己感知的寻泊成本和泊车费选择泊位，平台根据用户的选择进行分配。

2.2 平台分配模型

由于用户泊车有不同偏好，不同时段或不同位置的泊位对应不同的报价是合理的，平台提供多种型号的泊位供用户选择，优先分配先到的用户，满足用户偏好，模型的目标是在确定关键路径的情况下，按用户偏好进行依次分配，泊位分配模型如下：

为了方便分析，变量用以下符号表示。

P：泊车位集合，P={1,2,…,m}；

D：用户集合D={1,2,…,n}；

ei：单位时间泊位i的使用成本；

sj：用户j开始泊车时间；

dj：用户j泊车结束时间；

bj：用户j的报价，表示用户j的第一偏好报价，表示用户j的第二偏好报价；

qj：用户泊车信息，qj={sj,dj,bj}；

pj：j用户的支付价格；

fj：平台从用户j得到的利润；

Y：平台收益。

并做以下假设：

（1）对于每一个泊车位i∈P，对应一个使用成本ei，假设使用成本中没有考虑寻泊成本，泊车位按照使用成本ei由高到低降序排列。

（2）假设平台有私人泊位、公共泊位、CBD配套泊位三种类型，每种类型包括多个泊车位，每种型号的单价各不相同。

（3）假设有n个用户泊车，平台对用户按照开始使用时间升序排列，对于每个用户j∈D，用户的泊车信息为qj={sj,dj,bj}，泊车位按照使用时间段分配给用户，其中元素xji表示的是第j个用户是否分配到第i个泊位的状态。当xji=1表示第j个用户分配到第i个泊位，xji=0表示第j个用户没有分配到第i个泊位，使用时间段为{sj,dj}。给定泊位总数m，各个泊位的单位时间成本ei，用户总数n，所有用户的预约集Q，其中qj={sj,dj,bj}。平台从用户j得到的利润为fj，则j的支付价格[22]为：pj=fj+ei(dj-sj)。

在每一个时间间隔，平台将每个泊车位对应的用户按照时间先后顺序排列，将申请每一个泊位的用户按照偏好顺序分为第一偏好组合、第二偏好组合等。对申请每一个泊位的所有偏好组合，应用关键路径法分配，优先分配第一偏好的泊车位对应的用户，收益最大化模型如下：

约束条件：

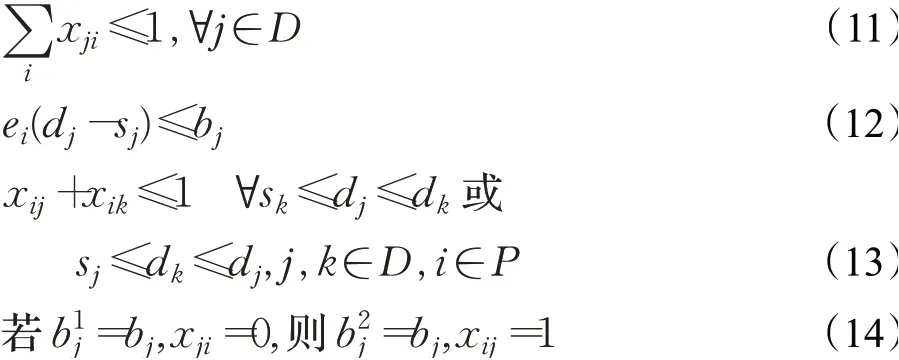
约束条件（11）为对于每个用户j，最多只会分配1个泊车位i；（12）表示只有用户j的竞标价大于i的服务成本，平台才有可能将i分配给j；（13）表示对于同一个泊车位i，若两个用户j和k的使用时间段冲突，则i只能分配给j和k中的一个；（14）考虑泊位分配过程中的用户偏好，表示在泊位i的第一偏好没有满足时，平台按第二偏好分配，以此类推。同时，平台寻求最多的用户，保证收益最大化。

假设平台采用智能泊车诱导系统，偏好分组法的分配程序如下：

（1）将泊车位的单位时间成本ei由高到低排序，给对应泊车位编号，得到泊车位集合C={1,2,…,m}，成本集合E={e1,e2,…,em}，竞价bj包含每个用户的第一偏好价格、第二偏好价格等。

（2）所有用户按照偏好组合分类，第一偏好对应的同一个泊位为一组。对每一个用户偏好集D的用户，按照开始使用时间sj升序排序，按照关键路径法筛选出预订时段互不冲突的用户组合为该泊位的“最佳组合”，将这些用户分配至“最佳组合”，用户收到反馈结果后分配结束，如该泊位有其他可共享时段，平台会及时更新可共享的时段范围。

（3）若用户没有分配到第一偏好的泊位，平台按照第二偏好集D′进行组合，按照关键路径法筛选出预订时段互不冲突的用户组合为该泊位的“第二最佳组合”，直至该时段内全部的申请分配完毕。

（4）按照每一个泊位i的第一偏好、第二偏好等，求出平台的收益。

下面通过一个算例来说明平台分配时考虑用户偏好的分配方法。

3 算例仿真

通过问卷调查，泊车用户的选择在不同情境下是不同的，既受泊车费、步行距离、巡航成本的影响，也受非理性因素的影响。算例中用户可以选择三种泊车偏好，具体数据来源于问卷调查。假设共享时段为7：00—16：00，时间窗口划分为30 min的时间间隔，共享第一个时段开始前6：30—7：00，以8个用户竞争CBD附近的3个泊位{A,B,C}为例，如选择等待CBD泊位，需要等待3 min，如选择私人共享泊位，泊车费增加到1元/15min（与CBD泊位0.5元/15min比较）；如选择公共共享泊位，步行距离增加500 m（与CBD泊位比较），泊位开放时段信息见表3。按泊车开始时间先后为序将用户列表，在6：30—7：00，用户报价参数见表4，报价表中三位数字分别表示用户给泊位A、B、C的报价，数字上标1、2、3表示用户的偏好顺序，其中有的用户只选择了一种类型的泊位，其余泊位的偏好报价为0。三个泊位{A,B,C}的成本单价降序排列为{9,8,6}，除了用户7，其余用户的报价均高于泊车位的成本。

表3 泊位开放时段表Table 3 Opening hours of slots

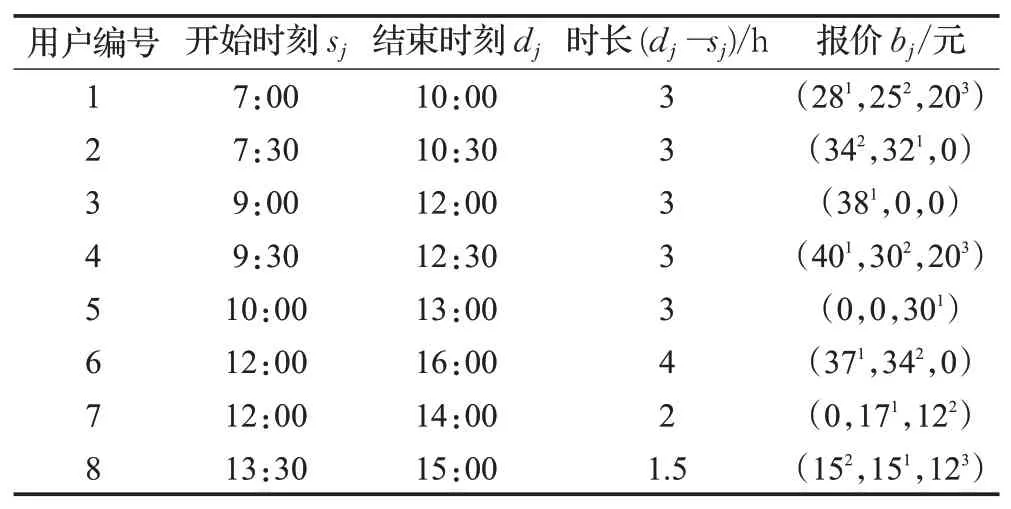
表4 用户报价参数Table 4 Users bidding parameters

在共享时段开始前的6：30—7：00，平台优先给第一偏好的泊车位A分配用户，1、3、4、6用户的第一偏好为泊位A，2、7、8用户的第一偏好为泊位B，5用户的第一偏好为泊位C，从7：00到14：00，每30 min为一个时段间隔，A的第一最佳组合为3，6，将3，6分配给A，更新A的可共享时段为7：00—9：00；同理，B的第一最佳组合为2、7，将2、7分配给B，更新B的可共享时段为10：30—12：00；C的第一最佳组合为5，将5分配给C，更新C的可共享时段为7：00—10：00、13：00—16：00。

用户1、4没有满足第一偏好，其第二偏好都为B，B更新后的共享时段满足不了用户1、4的泊车要求，用户8没有满足第一偏好，其第二偏好为A，A更新后的共享时段无法满足其要求。

用户1、4的第三偏好都为C，C的共享时段7：00-10：00，满足1的泊车要求，更新C的可共享时段为13：00-16：00。

用户8的第三偏好为C，C的共享时段13：00—16：00满足8的泊车要求，更新后C的可共享时段为13：00—13：30、15：00—16：00。最后在本时段内，只有用户4没有分配到泊位，只能在下个共享时段7：00—7：30内分配，偏好组合的泊位分配见图1。采用偏好分组的平台收入为188元（20+34+38+30+37+17+12），成本为148元（7×9+5×8+7.5×6），平台利润为40元。

图1 偏好组合法的泊位分配Fig.1 Slots allocation of preference combination method

为凸显偏好分组法的优势，与采用以最大化平台收益的关键路径法比较。平台优先给成本高的泊位A分配用户，除去用户5、7，其余6个用户的竞价满足要求，泊位A可用的用户集合D′={1,2,3,4,6,8}，构建时间分配矩阵R，初始化每个元素为0，对于D′中的任一个用户j，如果下一个用户的开始时间小于上一个用户的结束时间，则不考虑分配，如r12。由rj=bj-ei(dj-sj)求其rj：

再对D′={1,2,3,4,6,8}中的任意用户1，2，3，4，6，8，求其rjk，k＞j，k∈D′。得到泊位A的分配矩阵：

泊位A的关键路径为0-3-6-9，则将泊位A分给{3,6}。从用户集合中删除{3,6}。

同样，对于泊车位B：

泊位B的关键路径为0-2-8-9，则将泊位B分给{2,8}。从用户集合中删除{2,8}。

对于泊车位C：

从0到9的关键路径为0-5-9，则将泊位C分给{}5，从用户集合中删除{}5。

采用关键路径法的分配如下：用户3和6被分配到泊位A，用户2和8被分配到泊位B，用户5被分配到泊位C。

采用关键路径法的平台收入为154元（38+37+34+15+30），成本为117元（7×9+4.5×8+3×6），平台利润37元，用户3，6，2，8，5分别得到泊位，用户1、4、7没有获得泊位。按照关键路径法，用户2、3、5、6、8分得泊位，而偏好分组法中，用户2、3、5、6、7以第一偏好的价格分得泊位，用户1、8以第三偏好的价格分得泊位，两种方法的支付价格对比如表5所示。

表5 关键路径法和偏好组合法对比Table 5 Comparison of critical path method and preference combination method

通过对比，偏好分组考虑多种泊车价格，考虑了用户泊车的偏好，分配了更多的用户，同时平台的收益更高。

4 结论

在共享泊位分配过程中，既考虑了用户的泊车偏好，又考虑了平台的收益，泊位分配过程更加公平。在考虑泊车费时只分析了一个时间间隔内的竞价，没有考虑整个共享时间内的竞价。另外，用户偏好是根据问卷调查得出的，代表性不全面。以后的研究将主要在这两个方面加强。