翼型颤振压电俘能器的输出特性研究1)

田海港 单小彪 张居彬 隋广东 谢 涛

(哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨 150001)

引言

振动能量俘能器是被认为一种有潜力、能替代的能量源，能够有效持续为低功率微机电系统供能[1-3].振动-能量转换机理通常包括压电式[4-5]、电磁式[6]、静电式[7]和摩擦电式[8-9].由于压电式在易制作、高能量密度和无电磁干扰等方面具有巨大优势，已经成为国内外学者研究的热点.

流激振动广泛存在于自然环境中，蕴涵巨大的能量，包括涡激振动[10-11]、尾流激振[12-13]、颤振[14-15]和驰振[16-17].其中颤振是一种自激励、大幅值的气动弹性振动.当来流风速超过临界颤振速度时，压电俘能器发生颤振，并出现极限环振荡(limit cycle oscillations，LCO).学者利用翼型颤振俘获能量已经进行了理论和实验研究.Wang 和Inman[18]提出了一个同时能量俘获和振动抑制的压电多功能翼型梁，并获得了较好的结果.Abdelkefi 等[19-20]研究了含有间隙非线性翼型压电俘能器，表明间隙能降低颤振速度.Benjamin 和Bryant[21]实验研究了两个串行机翼的振动特性，获得了LCO 和涡旋特性.Wu 等[22]提出了双沉浮的翼型颤振压电俘能器，利用动态失速模型研究了动力学响应特性.Li 等[23]在翼型压电俘能器上采用非线性磁力，用于降低临界速度和拓宽频带，从而提升了俘获性能.

在二自由度沉浮-俯仰振动压电俘能器系统中，采用的气动力模型通常包括准静态[24]、非定常[25-26]和动态失速模型[27-28].De Marqui 和Erturk[29]采用非定常模型推导了翼型压电俘能器的压电-气动弹性振动无量纲方程，研究了结构参数对颤振速度和输出功率的影响.Li 和Xiang[30]采用非定常气动力模型研究了具有立方刚度非线性的气动弹性振动响应，获得了LCO 特性.为了研究机翼附近的流场和涡脱特性，国内外学者采用计算流体动力学(computational fluid dynamics，CFD)进行了仿真分析.Lu等[31]研究了非对称正弦俯仰运动对NACA 0012 翼型气动特性的影响，获得了机翼前缘的涡脱特性.Chen 等[32]分析了尾流对半主动拍振翼型压电俘能器的影响，表明尾流能增加提升力和降低力矩.

虽然国内外学者对二自由度翼型颤振压电俘能器进行了研究，但机翼附近的流场特性和涡旋脱落还不清楚.基于非定常气动力模型的理论分析不能获得机翼附近的流场特性.准确的流场特性能为提高振动响应和输出性能提供一定的指导.

因此，为了有效俘获气动弹性振动能量，在提出翼型颤振压电俘能器[33]的基础上，进一步研究压电俘能器的结构参数对其流场特性、气动弹性振动响应和俘获性能的影响.基于非定常气动力模型，推导压电俘能器流-固-电耦合场的数学模型.采用CFD 建立有限元模型，获得机翼附近的涡旋脱落和流场特性.搭建风洞实验系统，制作样机，验证理论分析和仿真模拟的正确性.仿真分析偏心距对气动弹性振动响应和俘获性能的影响.

1 翼型颤振压电俘能器的建模

1.1 压电俘能器的设计

以翼型作为扰流体截面形状，提出的二自由度翼型颤振压电俘能器模型如图1 所示.为了有效俘获气动弹性振动能量，压电俘能器竖直放置在空气流中.两个板簧由支架和机翼轴连接机翼，能发生垂直于来流方向的弯曲振动，用以模拟机翼的沉浮运动.弹簧丝一端插入机翼轴中，另一端与支架连接，限制机翼轴大角度的旋转，用以模拟俯仰运动.当空气来流作用于机翼表面时，随着来流风速的增加，气动力负阻尼系数逐渐超过压电俘能器的结构阻尼，系统的整体阻尼由正变为负，使其变为不稳定.压电俘能器发生颤振，表现为垂直于来流方向的沉浮运动和绕机翼轴的俯仰运动，并表现LCO.为了有效俘获气动弹性振动能量，将压电片PZT 粘贴在板簧根部，制作压电俘能器.压电俘能器的沉浮运动驱动板簧产生弯曲变形，俯仰运动经支架转换为板簧的弯曲变形.由于正压电效应，压电片在外接电阻两端产生交变的电流.设计的压电俘能器期望能实现较好的气动弹性振动响应和俘获性能.

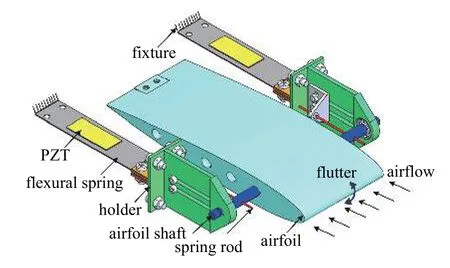
图1 二自由度翼型颤振压电俘能器模型Fig.1 Model of two degrees of freedom airfoil-based flutter piezoelectric energy harvester

1.2 压电俘能器的数学模型

根据经典的二元机翼理论，将机翼等效为刚体.机翼在来流中发生的气动弹性振动能被视为二自由度沉浮-俯仰运动.图2 表示压电俘能器系统的原理示意图.

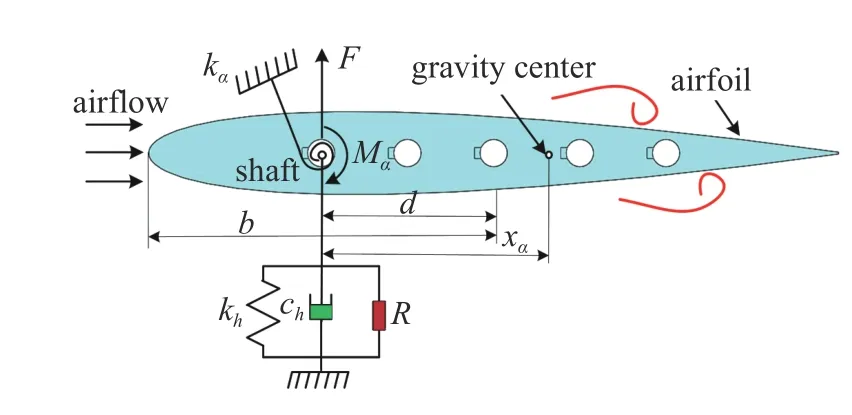
图2 压电俘能器系统的原理图Fig.2 Schematic diagram of piezoelectric harvester system

当来流作用于机翼表面时，产生垂直于来流方向的气动升力和绕机翼轴的气动力矩.在1/4 弦长处气动升力和绕机翼轴的力矩分别定义为F和Mα.压电俘能器系统二自由度沉浮-俯仰运动的控制方程可写为[33-34]

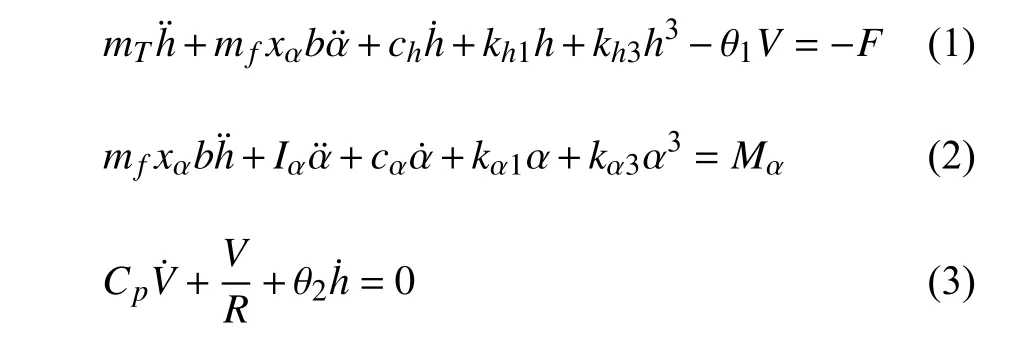
式中，h和α分别表示沉浮和俯仰位移，xα表示机翼轴与重心的无量纲偏心距，b表示半弦长，mT是压电俘能器系统总质量，mf仅表示机翼质量，ch和cα分别表示在沉浮和俯仰自由度上的阻尼系数，kh1和kα1分别是在沉浮和俯仰自由度上的线性刚度系数，kh3和kα3分别表示立方刚度系数，θ1和θ2分别表示机电耦合系数，R是外接电阻，V表示外接电阻两端的输出电压，Cp是压电俘能器的电容.

相对于准静态和动态失速气动力模型，非定常气动力模型采用Wagner 函数和Sears 近似描述不稳定的振荡效应，并考虑气动弹性系统的瞬时运动.为了准确地表示机翼的气动性能，本文采用非定常气动力模型，可写为[33，35]

式中，表示增广变量，d表示机翼轴到半弦长的无量纲距离，d=-0.5，c0=1，c1=0.165，c2=0.045 5，c3=0.335，c4=0.3.

将式(4)～ 式(6)代入式(1)～ 式(3)中，引入空间状态变量x=(h，α，，V)T，压电俘能器系统流-固-电耦合场的数学模型可写为

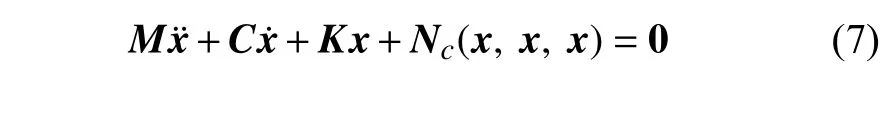
式(7)可利用龙格-库塔方法进行离散数值求解.

1.3 压电俘能器的有限元模型

流-固-电耦合是一种复杂的多物理耦合场，涉及到流体、结构和电学之间的交互作用.实验和理论分析不能揭示其耦合作用.为了分析机翼附近的涡旋脱落和流场特性，本文也采用CFD 方法，揭示机翼附近的流场特性和实时提取气动力和力矩，能够实时获得流场特性、振动响应和俘获性能.图3表示建立的压电俘能器有限元模型.

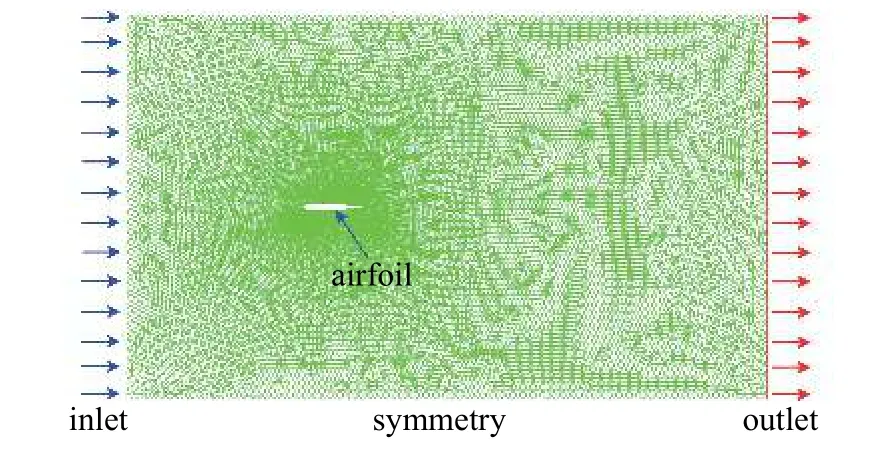
图3 压电俘能器的有限元模型Fig.3 Finite element model of piezoelectric harvester

为了展示机翼附近的流场特性和涡旋脱落，流场域设置为20b× 12b.边界条件包括入口(inlet)、出口(outlet)、对称(symmetry)和壁面(airfoil).有限元模型的网格数量为46 887.式(1)～ 式(3)利用龙格-库塔方法进行离散，编写为UDF (用户自定义函数)文件，在仿真分析中进行编译和加载.其中，气动力F和力矩Mα可以在仿真分析中实时求得.时间步长设置为0.001，总步数为15 000.采用基于k-ω的剪切应力传输(SST)模型能够准确的预测流场.求解过程为:(1)流场求解在时间Δt1和位置(h1和α1)下的F和Mα;(2)获得的F和Mα代入式(1)～式(3)中进行求解气动弹性振动响应和俘获性能，并在Δt2运动到新位置(h2和α2);(3)一个计算周期完成，直至达到所设定的求解时间.

2 实验验证和分析

2.1 风洞实验系统

图4 表示风洞实验系统.设计的风洞在测试段能保持稳定均匀的风流.风速调节范围为0～ 22.73 m/s.压电俘能器由设计的夹具竖直放置在测试段.数据采集系统包含NI 采集卡、风速仪和电脑，能够实时采集、显示和记录压输出电压.

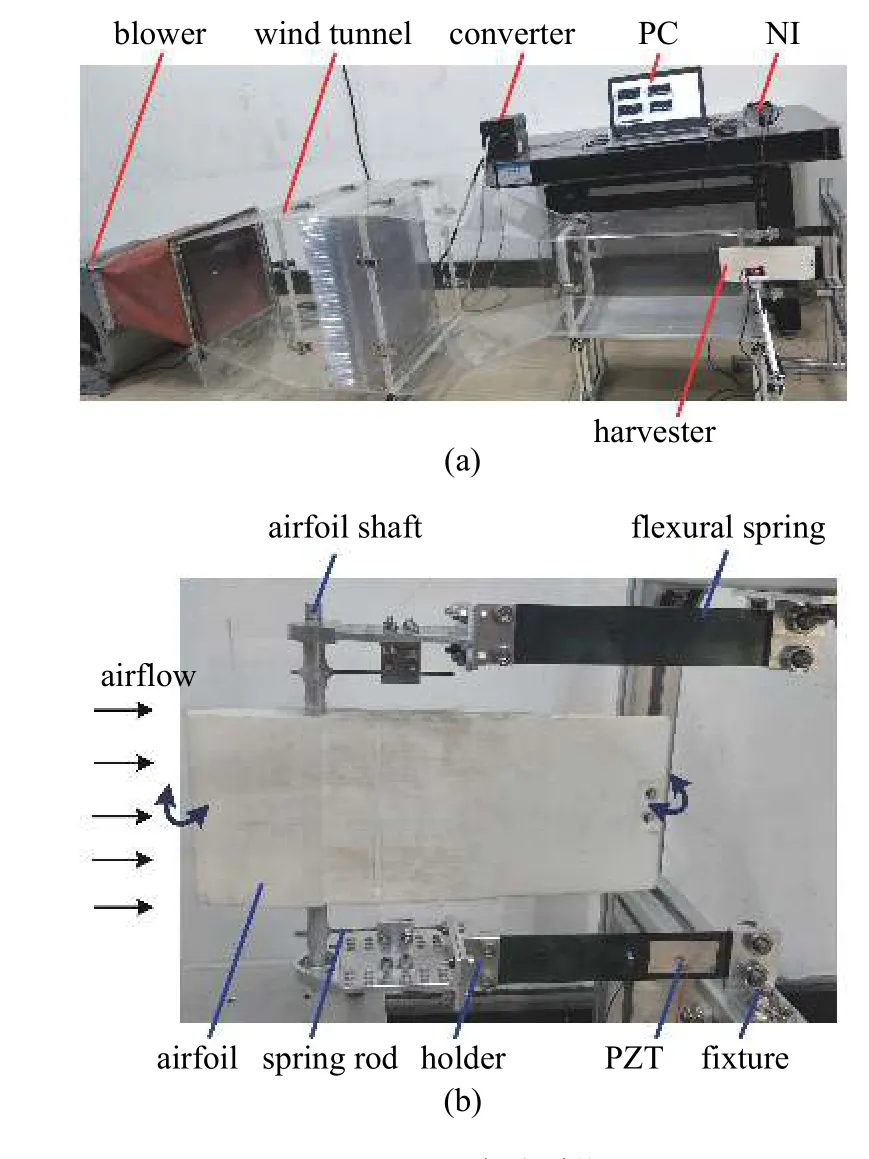
图4 风洞实验系统Fig.4 Wind tunnel experimental system

采用NACA 0012 作为翼型形状，半弦长为0.126 m.机翼采用3D 打印制作.压电俘能器的结构参数如表1 所示.其中，刚度系数通过力-位移曲线获得;阻尼系数由自由振动衰减曲线求得.压电俘能器的长，宽和高分别为0.3 m，0.03 m 和0.21 m.

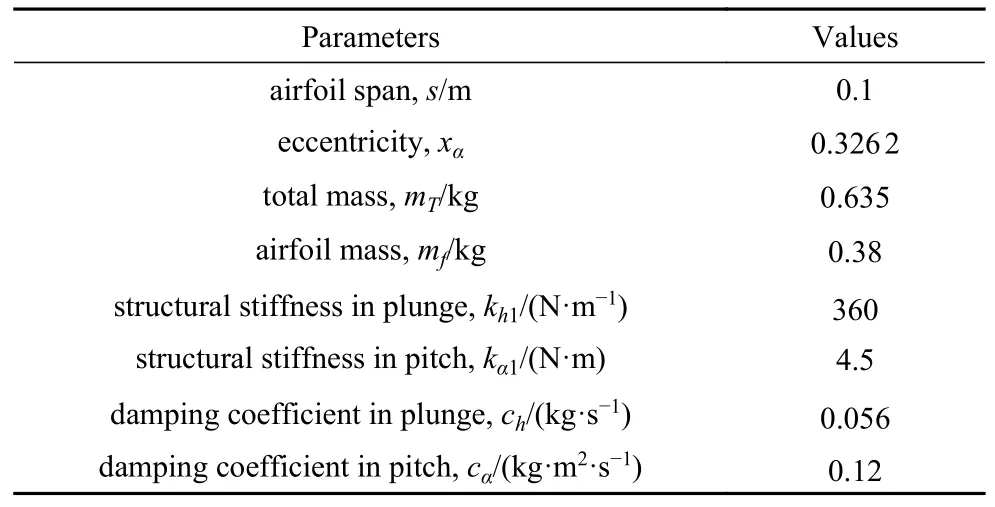
表1 压电俘能器的结构参数Table 1 Structural parameters of piezoelectric harvester

2.2 实验验证

本节采用实验方法，对数学模型求得的理论值和仿真分析获得的仿真值进行验证分析.图5 表示实验、理论和仿真获得的输出电压随风速的变化曲线.其中，输出电压指的是均方根值.

由图5 可知，压电俘能器的输出电压随着风速的增加首先几乎为零，接着迅速增加，最后逐渐平缓.这主要是因为当风速超过压电俘能器的颤振起始速度(11.3 m/s)时，发生颤振，并表现为LCO.理论和仿真分析获得的输出电压与实验值有较好的一致性，特别是风速在12.2～ 14 m/s.但在较高风速下，存在一定的误差，主要是较大的变形导致压电俘能器系统的非线性特性.总之，理论和仿真分析能较准确地预测颤振速度和评价俘获性能.

3 振动响应和俘获性能的仿真分析

上节利用实验和理论分析验证了仿真模型的正确性.本节采用仿真方法分析压电俘能器的流场特性、气动弹性振动响应和俘获性能.

3.1 流场特性

为了获得机翼附近的流场特性和涡旋脱落，图6表示机翼附近的压力场变化云图.其中，虚线表示机翼沉浮运动的初始中间位置;压力变化范围为-50～80 Pa.

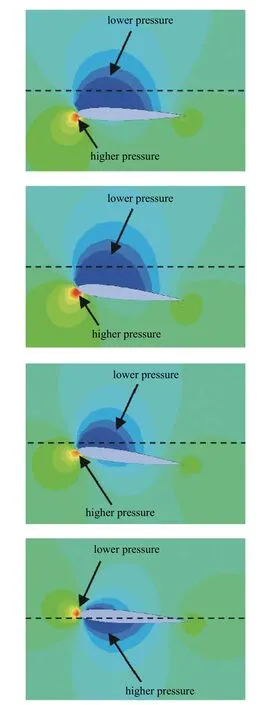
图6 机翼附近压力场变化云图Fig.6 Variation of pressure field around the airfoil

图6 表明机翼首先以较大沉浮速度离开中间位置向下运动，此时高压区域出现在机翼前缘下表面，低压区域出现在机翼上表面.由于高压区域出现在机翼前缘下表面，机翼接着发生顺时针的旋转运动.此外，由于负压的吸力作用，阻止机翼继续向下运动.在机翼上下表面的压力差驱动机翼向上运动，并伴随着顺时针的旋转运动.机翼继续运动接近中间位置，高压区域出现在机翼前缘上表面.因此，交替的压力差驱动机翼发生在竖直方向上的沉浮运动和绕机翼轴的俯仰运动.由于较大的机翼弦长和较小的俯仰幅值，涡旋始终附属在机翼表面，并没有在机翼尾缘发生脱落.

3.2 气动弹性振动响应

压电俘能器的气动弹性振动响应决定着俘获性能.图7 表示压电俘能器在15.2 m/s 时沉浮和俯仰运动的时间变化曲线、功率谱密度和相位图.

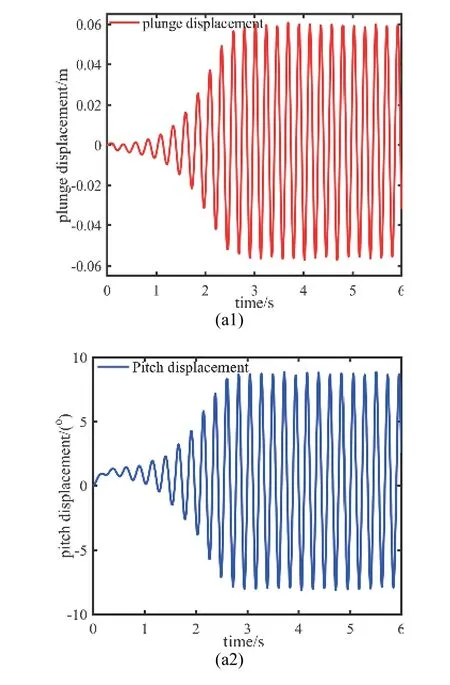
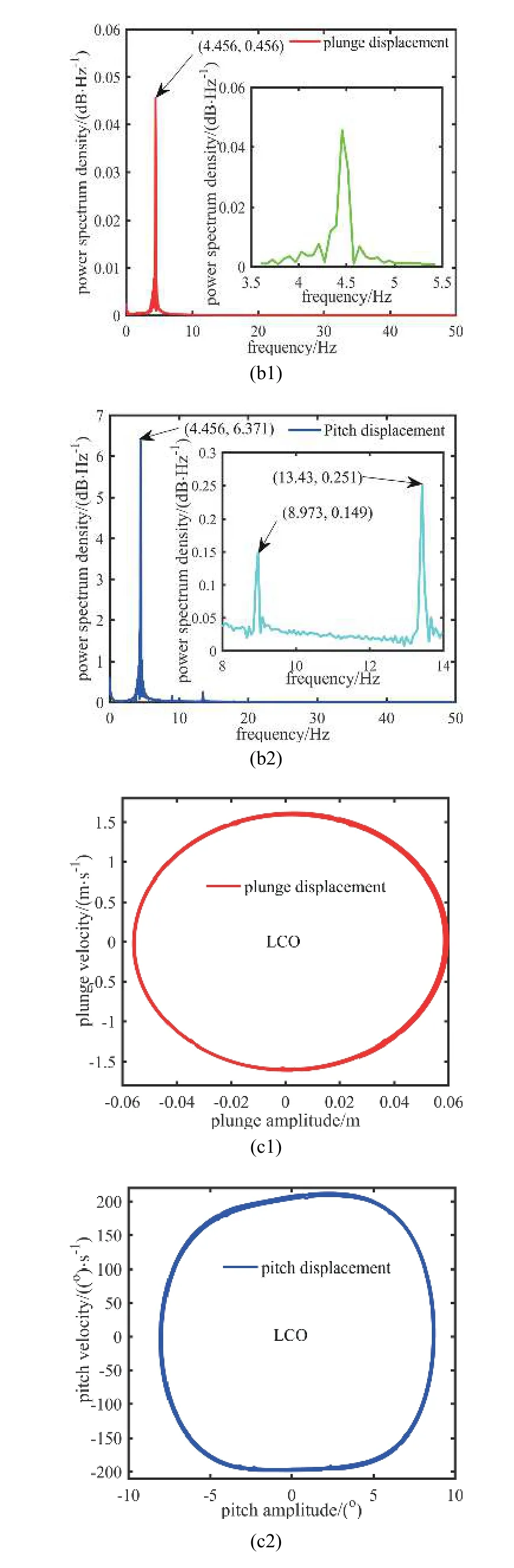
图7 在15.2 m/s 时沉浮和俯仰运动的时间变化曲线、功率谱密度和相位图Fig.7 Time history，power spectrum density and phase portraits in plunge and pitch at 15.2 m/s

由图7(a1)和图7(a2)可知，沉浮和俯仰位移需要大约3 s 实现周期性和稳定的振动.通过快速傅里叶变换(FFT)，俯仰运动的一阶基频为4.456 Hz，是等于俯仰运动的.表明压电俘能器系统发生颤振，在沉浮和俯仰运动中存在耦合作用，产生等幅值自激励的气动弹性振动.同时，俯仰运动也出现二阶和三阶频率，表明压电俘能器系统具有俯仰平方和立方刚度非线性.立方频率的幅值大于平方的，因此，俯仰立方非线性刚度系数对系统的振动特性具有重要影响.图7(c1)和图7(c2)表明沉浮和俯仰位移的相位图表现单圆环.这意味着压电俘能器在15.2 m/s时发生LCO，是适合于俘获能量.

3.3 俘获性能

为了充分的研究压电俘能器结构参数对其气动弹性振动响应和俘获性能的影响，采用重心与机翼轴之间无量纲偏心距进行研究.图8 表示压电俘能器的沉浮幅值，俯仰幅值，输出电压和输出功率随偏心距和风速的变化曲线.其中，压电俘能器外接负载电阻为250 kΩ.

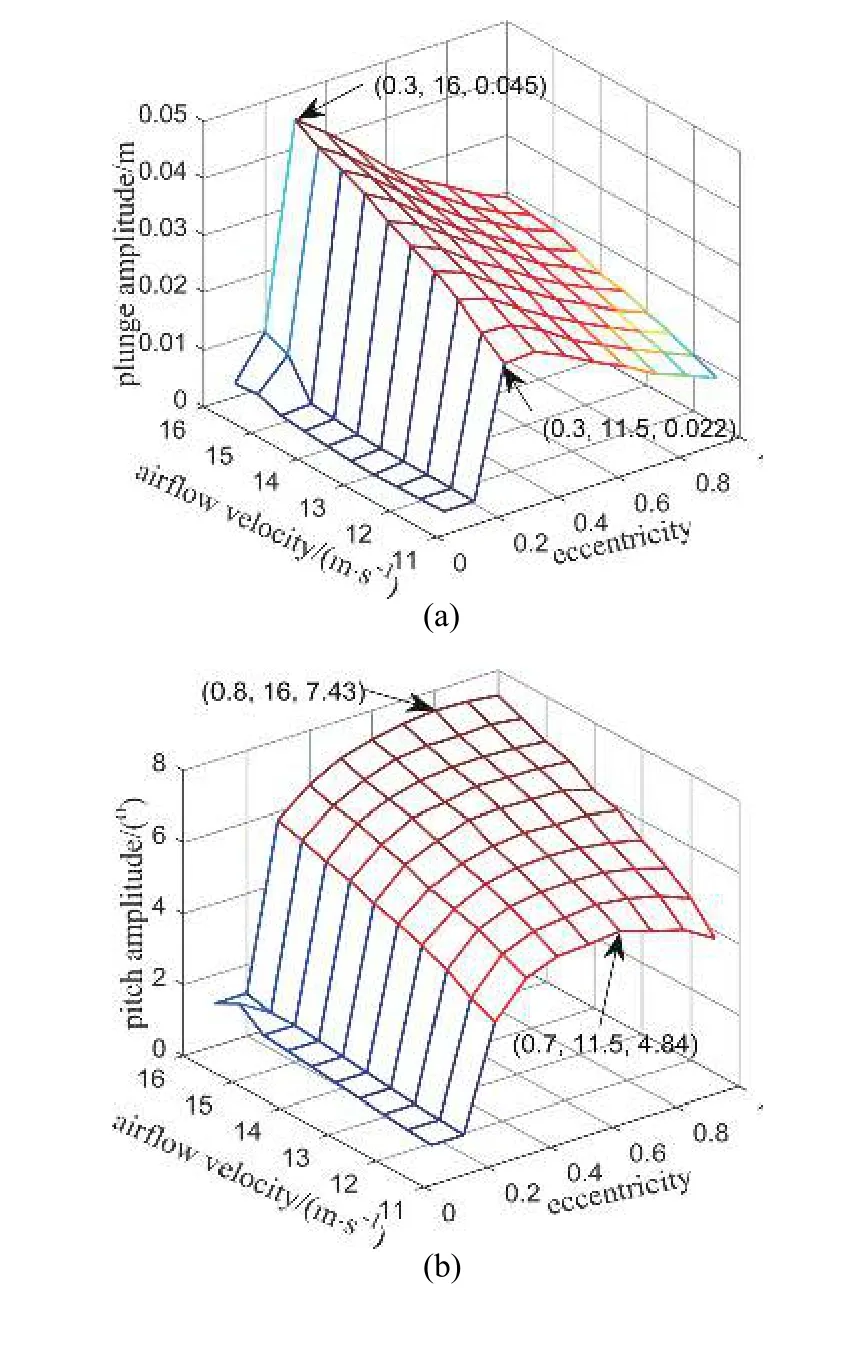
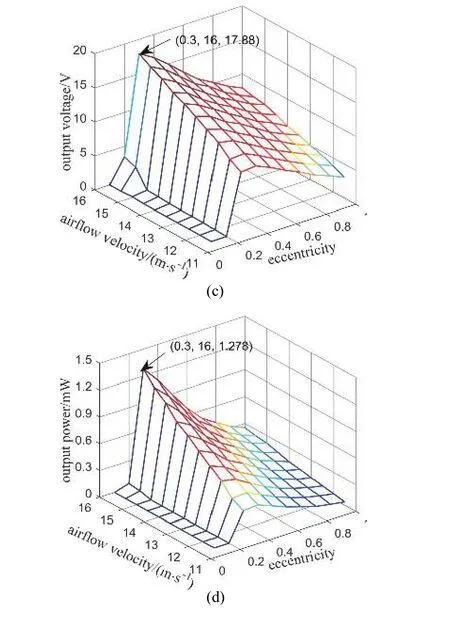
图8 沉浮幅值，俯仰幅值，输出电压和输出功率随偏心距和风速的变化曲线Fig.8 Variation of plunge amplitude，pitch amplitude，output voltage and output power with eccentricity and airflow velocity

由图8(a)可知，偏心距和风速对沉浮幅值具有重要影响.随着偏心距的增加，沉浮幅值首先迅速增大，直到达到最大值，然后缓慢减小.这主要是因为偏心距决定颤振速度，从而影响气动弹性振动响应和俘获性能.而风速的增加也导致了沉浮幅值的单调增加.输出电压和输出功率与沉浮幅值的变化趋势相似.当偏心距为0.3 和风速为16 m/s 时，可获得最大沉浮幅值为0.045 m，输出电压为17.88 V，输出功率为1.278 mW.此外，偏心距和风速对俯仰幅值产生不同的影响.当偏心距增大时，质量惯性矩也相应增大，导致俯仰幅值一直增大，如图8(b)所示.而较大的沉浮幅值和较小的俯仰幅值有利于俘获气动弹性振动能量.这解释当偏心距为0.3 时，能得到最大的俘获性能.该结构参数下压电俘能器的功率密度达到7.99 mW/cm3，相比较于已经报道的翼型颤振压电俘能器[36]，其输出功率为2.2 mW，压电材料体积为0.481 cm3，功率密度为4.57 mW/cm3，可实现较好的俘获性能.因此，选择恰当的压电俘能器结构参数，能够促进气动弹性振动响应和提升俘获性能.本文能为设计高效的翼型颤振压电俘能器提供重要的指导.

4 结论

本文提出了一种翼型颤振压电俘能器，模拟机翼的二自由度沉浮-俯仰运动和俘获气动弹性振动能量.基于非定常气动力模型，推导了压电俘能器的流-固-电耦合场的数学模型.采用CFD，建立了压电俘能器的有限元仿真模型.搭建实验平台，制作了压电俘能器实验样机，进行了实验验证与分析.实验结果表明:仿真分析获得的输出电压与理论和实验值具有较好的一致性，验证了仿真模型的正确性.机翼附近交替的压力差驱动压电俘能器发生二自由度沉浮-俯仰运动.当风速超过颤振速度时，压电俘能器发生颤振，并表现为LCO.当偏心距为0.3 和风速为16 m/s 时，可获得最大沉浮幅值为0.045 m，输出电压为17.88 V 和输出功率为1.278 mW.输出功率密度达到7.99 mW/cm3，相比较于其他压电俘能器，能实现较好的俘获性能.本文能为进一步设计高效的翼型颤振压电俘能器提供重要的研究基础.