基于SVM的煤炭低位发热量软测量

潘红光，宋浩骞，苏 涛，马 彪

(1.西安科技大学 电气与控制工程学院，陕西 西安 710054；2.鄂尔多斯市神东工程设计有限公司，内蒙古 鄂尔多斯 017000)

0 引 言

煤炭作为中国的主要能源之一，煤炭质量分析在煤炭的开发、利用过程中发挥着不可或缺的作用[1]；而煤炭低位发热量是煤炭质量分析中最常用的评价指标[2]。因此，煤炭低位发热量的准确、快速测量已成为实际生产的迫切要求。对煤炭低位发热量的测量，常规方法为氧弹热量法，该方法需要取样离线分析，且操作复杂、分析周期长[3]。虽然工业应用中还有其他硬件测量方法，但普遍存在测量设备笨重、昂贵、费用大等缺点，且不能较好地了解煤炭低位发热量的影响因素。

相比较而言，软测量方法解决了硬件测量的经济性等问题，且具有简单、实用、反应迅速的特点。软测量的基本思想是在较为成熟的硬件传感器基础上获得数据，以计算机技术和算法为核心，利用相关变量建立模型对主导变量进行间接测量[4]。 软测量的建模方法有很多，一般可分为：机理建模、回归分析、状态估计、模式识别、人工神经网络、模糊推理、LSTM(long short term memory)网络、基于支持向量机(support vector machine，SVM)和基于核函数的方法等[5]。其中，SVM可以不依赖训练样本的数量和质量，即对小样本问题也能保证推广性，且具有严格的数学基础和理论推导、较强的逼近能力和泛化能力[6]。基于SVM软测量模型的经典研究有：YANG等基于支持向量机的软测量模型，实现了不同煤种燃烧产生NOx浓度的测量[7]；CHEN 等基于SVM的软测量模型，利用实测气象变量实现了三峡库区月蒸发量的完美预测[8]。此外，软测量应用中具有代表性的BP神经网络和具有记忆能力的LSTM网络也取得了一些显著性的成果，如：吴采用BP神经网络通过分析电厂实际数据，对燃煤电厂SO2的排放量进行了监测[9]；陈等人基于LSTM网络，利用水轮机组的时间序列数据进行建模，并成功应用于某水电厂水轮机组运行状态的检测[10]。

目前对煤炭低位发热量的测定，主要运用多元线性回归式等从实验和理论上对煤炭低位发热量进行预测和影响因素分析[11-13]。首先采用SVM进行软测量建模，并与具有代表性的BP神经网络模型和在时间序列变现突出且具有记忆功能的LSTM软测量模型进行性能比较；然后，采用均方误差和均方相关系数对模型进行分析比较，结果表明基于SVM的软测量模型精度和稳定性更好，进一步在基于SVM的煤炭收到基低位发热量的软测量模型上从应用的角度分析了煤炭低位发热量的影响因素。

1 软测量方法

1.1 SVM基本原理

SVM是在统计学习理论上建立起来的一种机器学习方法[14]，主要思想为：设有i个样本(x1,y1),(x2,y2),…，(xl,yl),其中，xi为样本输入;yi为样本输出，且xi∈Rn，yi∈R,i=1,…,l,首先将样本数据映射到高维空间Φ(xi,x)，然后用函数f(x)进行拟合回归，并通过拟合期望风险函数最小化来实现最优估计[15]。

1.2 基于SVM的回归问题

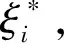
(1)

(2)

式(2)的解αi有一部分不等于零，对应样本数据被作为支持向量，得到回归函数为

(3)

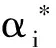
对于非线性问题时，首先需要将低维样本空间的非线性问题映射成高维空间的线性问题，然后才可以利用式(2)和式(3)进行计算[17]。由于空间映射后维数增加，计算量明显增大，算法的复杂性提高。考虑到式(2)，式(3)只用到内积运算(xi·xj)，根据泛函数的理论，映射高维空间的内积运算可用原低维空间的核函数进行代替，所以直接用核函数K(xi,xj)代替内积运算(xi·xj)[18]。

(4)

相应的回归函数就变为

(5)

1.3 SVM算法的优越性

一般地，神经网络在进行非线性建模时，需要预先设定网络结构及节点数，然后通过修正算法对固定节点数的权重进行迭代修正，且之后不随新样本的加入而改变。然而，支持向量机的建模技术不同于神经网络建模技术。利用支持向量机建模时，随着新学习样本的加入，不仅支持向量对应的支持值会发生变化，而且支持向量的数量也会改变，进而达到较好建模效果[19]。采用迭代方式对支持向量及其支持值进行实时修正是SVM应用于建模的关键，其取决于核函数的选择和参数的调整。与其他建模方法类似，核函数的选择和参数的调整取决于过程调整的经验[20]。

2 数据分析

2.1 数据采集及预处理

本研究数据为中国陕西省榆林市某电厂的实际生产数据，数据采集时间为2019 年1 月1日到7月16日，采样时间间隔为1 d，共197组数据，且每组数据都由当天多组数据经过随机误差处理后得到；采集数据主要为煤质的工业分析数据，包括：全水(收到基水分)、空气干燥基水分、空气干燥基灰分、固定碳、空气干燥基挥发分、弹筒发热量、收到基低位发热量(MJ/kg)、收到基灰分、干燥基硫、干燥无灰基挥发分、收到基硫、空气干燥基硫和收到基低位发热量(cal/g)。

实际生产数据除了需要进行随机误差处理外，还需进行粗大误差处理和数据归一化和反归一化处理[21]，其理论具体如下。

1)随机误差处理采用平均值滤波方法处理，取采样时刻的前后相同短间隔时间数据平均值作为样本数据，则样本数据xi为

(6)

式中xt为采样前后时刻数据；n为数据的个数。

2)粗大误差处理采用统计判别法3δ准则，设样本数据为：x1,x2,…,xl，则δ计算公式为

(7)

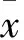
3)数据归一化和反归一化。采用min-max法进行数据归一化，先找出最大值xmax和最小值xmin，再经过下列公式算出归一化后的样本数据Xi

(8)

计算结果是在[0,1][22]，为了使数据结果更直观，还必须进行反归一化处理

[xi]=Xi(xmax-xmin)+xmin

(9)

式中 [xi]为反归一化之后的数据。

2.2 辅助变量选取

2.2.1 初选

根据机理分析对数据进行类似数据项和直接相关数据项进行剔除和筛选，即只是在量纲单位上不同[23]。因此，样本数据中的2个收到基低位发热量项属于类似数据项；固定碳的含量、收到基灰分含量，这几项数据直接相关于其他数据项，不能选做辅助变量。剔除后，剩下的全水、空气干燥基的水分、灰分、挥发分、硫，收到基硫、干燥基硫、干燥无灰基硫，弹筒发热量之间的数据间都具有独立性，均可作为模型建立的初选辅助变量。

2.2.2 精选

根据辅助变量和目标变量之间的相关系数的大小，进行相关性分析后进一步精选辅助变量，其中相关系数采用皮尔逊函数计算

(10)

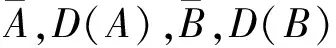
经计算，各相关系数见表1。辅助变量相关系数排序后，由于辅助变量太多会影响模型灵活性和时效性，过少又难以充分输入参数的特征信息[23]，所以较小相关系数中选取其较大的2个。筛选后剩余6个辅助变量，维度已经很小，降维处理作用不大。因此，精选的辅助变量为：全水、弹筒发热量、空气干燥基下的水分、灰分、挥发分、硫，目标变量为收到基的低位发热量。

表1 辅助变量与主导变量的相关性Table 1 Correlation between auxiliary and dominant variables

3 仿真结果及对比分析

硬件环境：CPU为Intel(R)Core(TM)i7-9750H，内存为DDR4 8G，显卡为NVIDIA GeForce GTX 1650；软件环境：LSTM 模型基于Python框架PyTorch 0.3.1，编辑环境为PyCharm 5.0.3；BP神经网络模型和SVM模型的环境为MATLAB 2015b。

3.1 数据分集及模型训练

由于软测量建模需进行模型训练和测试，所以，需将样本分为训练集和测试集。此外，数据集间合适的数量比可使网络学习得到的模型效果较好，且不存在过拟合[24]。因此，此处将样本前144组数据作为训练集，后50组数据作为测试集。

软测量模型的参数直接影响预测结果。在SVM的回归建模时，通过径向基RBF核函数的惩罚系数C和宽度系数σ进一步决定SVM的建模性能[25]。C是对超出规定ε精度的惩罚力度，C越大，训练误差会相应变小，但增大到某一数值后这种趋势会变小，甚至趋于零，其值一般在1～100；宽度系数与支持向量的紧密程度有关，值越小，支持向量之间联系越紧密，但过小容易造成过拟合，使泛化能力下降；反之越松弛，容易造成欠拟合，且一般在0.001～10[26]，用Libsvm 3工具箱来寻找两者最佳值，使其在上述范围内不断寻找误差最小的C和σ。

LSTM神经网络的参数设置，迭代次数不要太小，因为迭代次数与收敛性有关，但也有上限，最大迭代次数为5 000。学习率在0.000 1～0.001，不能过大；隐含层个数与可见层相差不能太大[27]。BP神经网络的参数设置时，主要考虑影响网络结构的参数，包括隐含层的节点个数、学习率和训练精度要求[9]。隐含层的节点个数凭借经验决定，个数过少，影响网络的有效性，过多会大幅度增加网络的训练时间。学习率通常设置在0.01～0.09，学习率和训练次数有关，一般来说，学习率越小，训练次数越多，但学习率过大，训练次数太少会影响网路结构的稳定性。训练精度的设定，需要根据输出要求来定，值越低则代表输出要求的精度越高[28]。3种模型参数选择见表2。

表2 网络模型参数Table 2 Network model parameters

3.2 对比分析

实验采用均方误差(MSE)和均方相关系数(R2)作为模型的评定标准，其中均方误差(MSE)的函数方程为

(11)

R2为回归平方和(SSR)与总离差平方和(SST)的比值。R2的值在(0,1)，越接近1，回归拟合度越高。其计算公式为

(12)

式中SSE为残差平方和，SSE+SSR=SST；且SSR,SST,SSE计算为

(13)

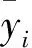
表3为3种模型的性能比较，从表3可以清晰地看出LSTM网络的2个评定参数值比BP网络的要好，证明了LSTM网络的测量精度要比BP网络有所提高，但两者的各个参数均和SVM模型存在明显差距。

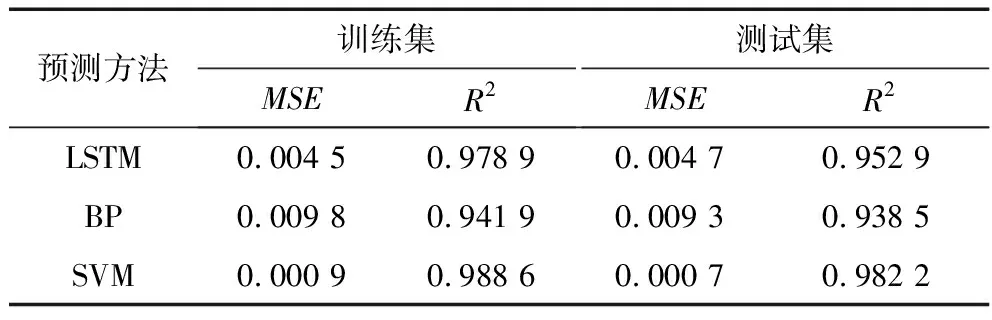
表3 3种方法结果比较Table 3 Results comparison by three methods

图1(a)为BP网络的预测结果，从测量效果看，BP网络的预测值与真实值的误差较大，而且存在部分点的趋势没有较好跟随，整体效果不是很好。图1(b)为BP的相对误差，部分点的相对误差接近3%，整体的相对误差值偏大。

图1 基于BP模型的仿真结果Fig.1 Simulation results of BP-based model

图2(a)为LSTM的预测结果，从整体的趋势来看，都可以与真实值跟随；而且预测值与真实值相差不大，相比BP有所改善。图2(b)为LSTM的相对误差，相对误差均在3%以下，且整体相对误差比BP小，满足工业生产要求。

图3(a)为SVM的预测结果，可以看出大多数预测值与真实值的点基本上重合，它们之间几乎不存在差异，所有点的趋势也完全跟随，整体效果最好且接近完美，满足实际生产要求。图3(b)为SVM的相对误差，大部分点的相对误差均在0.5%以下，主要集中在0.2%左右，完全满足工业生产要求。

从图1、图2和图3可以发现，基于SVM的预测精度比LSTM网络好，但两者均在第44点处的误差较大，基于BP网络在此点并未表现异常，且LSTM网络整体的相对误差缩小为BP网络的一半。由此说明对于神经网络，LSTM网络对这种时序性较强的数据比BP网络有更好的学习能力，准确度更好。对比三者的2个评定参数，SVM模型更有优势，精确度较为稳定，可信度更高，MSE比LSTM提升了80%，R2提升了3%。

图2 基于LSTM模型的仿真结果Fig.2 Simulation results of LSTM-based model

图3 基于SVM模型的仿真结果Fig.3 Simulation results of SVM-based model

因此，基于SVM的煤炭低位发热量软测量模型比BP和LSTM网络更具有优势，且完全满足实际生产要求。在这种时序较强的数据中，LSTM比BP网络有更好的学习能力，预测精度更好。

基于SVM的煤炭低位发热量软测量模型精度最高，可信度更高，所以在此模型基础上进一步研究各个辅助变量对煤炭低位发热量的影响。具体如下：在基于SVM软测量模型基础上，将各个辅助变量值依次置零，分析缺少本辅助变量后模型的测试结果，也采用上述MSE和R2来作为评定指标。表4为置零各辅助变量的测试结果，其排序是按照MSE的大小。

表4 置零不同辅助变量的测试结果Table 4 Test results of zero-setting different auxiliary variables

从表4可以看出，置零前5个辅助变量后两参数值均有所变差，其中置零弹筒发热量后模型的测试效果最差，其次是全水，置零空气干燥基水分后模型测试效果有所改变，但不明显。由此说明，在这些变量中，弹筒发热量对煤炭低位发热量的影响最大，其次是全水，空气干燥基水分有影响，但不明显；其他变量对煤炭低位发热量也有影响，但没有前面三者影响大。置零空气干燥基硫后，模型的MSE反而变小，R2变大，说明其对模型存在干扰作用，对煤炭低位发热量并无影响。

4 结 论

1)通过对在线数据进行软测量建模和比较，发现基于SVM的煤炭低位发热量软测量模型精度更高，可满足实际生产要求，能为生产提供可靠的参考数据。

2)从软测量应用的角度，分析了煤炭低位发热量的影响因素，发现弹筒发热量对煤炭低位发热量的影响最大，其次是全水，空气干燥基水分对煤炭低位发热量有较小影响。

3)该研究可进一步改进以获得更为稳定的模型或研究更为细微的影响，如：利用其他方法对模型参数进行动态跟随，提高模型稳定性，如粒子群算法等；在本研究的基础上，进一步研究其他变量对煤炭低位发热量的细微影响；对辅助变量进行组合置零，研究不同变量组合对煤炭低位发热量的影响。