基于Gerstner函数和JONSWAP海浪谱的海浪仿真

杨志钢，孙 鹏

(哈尔滨工程大学 信息与通信工程学院 先进船舶通信与信息技术工业和信息化部重点实验室，哈尔滨 150001)

海浪模型在诸多领域有着广泛的应用，并且一直是计算机图形学海浪场景研究的重点之一.海浪模型是整个海浪仿真的基础，模型建立的优劣决定了整个海浪波动的真实性和实时性.通常海浪场景的绘制比较复杂，且海浪具有真实性、随机性、多变性、广阔性等特性，针对海浪的特性，各国的科研学者分别从几何模型模拟、物理模型模拟、海浪谱模拟等方法对海浪场景进行建模.

几何模型模拟是指根据经验和数据总结得到数学方程来构建海浪模型的一种方法.最简单的模型是根据Airy波理论提出的，他假想振幅较小的海浪由一系列正弦波叠加而成，该方法是根据海浪的波动特性以及几何形状，结合函数使用几何曲线或者曲面来描述海浪的特性[1-2].经典模型中还包括：Peachy模型[3]、Stokes模型[4]、Gerstner模型[5]等，该类方法的优点在于建立海浪模型简单，数学函数的解易于求得，形成近似的海浪仿真模型.但由于数学函数简单，生成的海浪模型的波动比较单调，随机性弱，适用于风平浪静、轻轻涟漪的海面仿真.

基于物理模型的模拟方法是通过物理模型计算各个海浪参数来模拟海浪内部的各个水粒子的运动状态，进而生成海浪模型[6-7].该类方法参考的物理模型是流体动力学的Navier-Stokes方程式，该方程式是描述黏性牛顿流体的物理模型，由于其特性和海浪波动的特性类似，在进行一系列的数学近似计算后，可以模拟出海浪内部的水分子的任意时刻的运动状态[8-9].由于该方法是与海浪内部波动特性相关，而且详细的求解了各个水分子的运动状态.该类方法仿真出来的海浪细节清晰、真实感强，但是参数求解复杂、计算量大，适用于需要处理细节但是变化程度低和频率不高的海浪场景.

海浪谱模拟方法是根据真实观察所得，又根据数学方法总结而形成的一种方法[10-12].在海洋领域研究学者的多年观察和研究下，利用测量获得的海浪数据，通过统计方法[13]总结出了一系列关于海浪的谱模型，称为海浪谱[14-15](例如Neumann谱、Pierson-Moskowitz谱、JONSWAP谱)，海浪谱具有海浪的外部表现特征，又同时可以描述海浪内部能量分布的特性.该类方法可以表现出海浪的真实性，尽管其数学模型的计算量也大，但是优于物理模型的仿真方法，提高了仿真时要求的实时性和真实性.

通过对以上方法进行优劣分析，针对海浪的特性，提出了一种介于几何模型模拟和海浪谱模拟之间的方法，首先设计一组描述波浪的动态方程组，该方程组作为海浪的基本构造模型；然后，利用线性叠加函数方程组将二维函数扩展到三维模拟真实的海浪场景；最后利用JONSWAP海浪频谱的输出进行参数的设置，利用参数对提出的动态方程组进行三维控制以达到动态海浪的模拟.本文方法比简单利用海浪方程组叠加进行单一海浪模拟更加逼真，且模拟的海浪波动更有层次、更紧凑，与物理模型模拟相比复杂度低且计算量小.

1 海浪模型

1.1 Gerstner海浪模型

针对海浪的几何构造模型，从两个方面进行选取：一方面几何模型能够描述从涟漪海面到汹涌海浪的仿真；另一方面模型能够模拟各种海浪强度变化的海浪.

1986年Fournier提出了经典的Gerstner模型，从动力学的角度描述了海浪各质点的运动，Gerstner模型如式(1)所示:

(1)

图1 Gerstner摆线方程Figure 1 Gerstner cycloid equation

1.2 海浪三维线性叠加

图1是海浪的二维摆线图，而模拟真实的海浪则需要三维方程组，所以需要将二维方程扩展成三维方程组，而在扩展过程还需要针对海浪的流动性进行相关改进，在将单一波进行线性叠加的过程中，需要处理每个波长的方向角，此时方向角采用余弦函数，这样在波浪变换过程中使得幅度由高到低与真实海浪变换一致，变换后的三维方程组如式(2)，式(2)加入了多个波时海浪的叠加函数，其中θ为水平面时海浪的方向角，α为随机相位角，z(t)表示高度场叠加函数.

(2)

1.3 JONSWAP谱

有了模拟海浪的方程组后，需要获得振幅、相位、频率、相位参数来对方程组进行控制，进而通过时间参数来对海浪进行实时性的模拟，而参数的选取可以通过频谱生成器进行生成，例如Neumann谱、Pierson-Moskowitz谱、JONSWAP谱等都可以进行参数的获取，其中JONSWAP谱是加入了Pierson-Moskowitz的谱参数，不再把风速、风向作为频谱参数进行设置，而采用有效波高和波浪周期作为输入参数进行计算，在参数计算时更加稳定，适用性广，可以在各种海浪情况下进行谱参数提取，所以本文采用JONSWAP谱，其谱公式如式(3)所示：

(3)

其中式(3)中的各参数表达式如下：

χ=exp(-(f/fp-1)2/2σ2)

(4)

(1.094 0.01915lnγ)

(5)

(6)

(7)

其中：f为波浪频率，fp为谱峰频率，Tp为谱峰周期，H为有效波高，Th为波浪有效周期，γ为谱峰因子，本文取平均谱峰因子为3.30.

有了海浪谱还需要对连续谱离散化，选取符合海浪幅度变化的谱参数，通过对JONSWAP海浪谱进行参数提取，利用频谱参数对三维摆线方程进行控制，实现海浪的动态模拟，而频谱需要选则频谱能量集中的区域，在模拟海浪时更能体现变换程度，且频谱只需要适量选取即可，能使海浪变换情况复杂且更加真实，覆盖范围更广且计算量不大.

1.4 海浪网格绘制

实时绘制海浪模型时，需要将海浪进行三维程序实现，海浪几何模型通常可以由许多三角形或者四角形组合而成，本文为了描述海浪细节采用三角形结构建海浪模型，三角形个数越多组合成的曲面结构越细，仿真出来的海浪效果真实性会较高，但是会出现计算量大，实时性低等问题，所以在仿真时，根据海浪需求，需要在实时性和真实性之间进行平衡，从而设计出合理的三角形个数和网格结构.

本文在进行网格设计时，采用了正方形拓扑网格结构，运用了OpenGL图形库函数进行模拟，以下是形成海浪网格仿真的基本思想：1)获取整个海浪的空间位置坐标数据，将其存储在动态数值中；2)利用OpenGL对相邻三个空间位置坐标点进行连接，形成三角形网格，直到整个正方形拓扑网格连接完成，得到静态的海浪模型结构；3)通过时间参数和OpenGL的实时缓存功能进行空间坐标数据的更新，实现动态的海浪模拟.

2 实验仿真和结果

2.1 频谱生成

JONSWAP频谱的选取直接影响采样点个数的选取，计算的复杂度，以及生成不同海浪的真实性，从有效波高和有效周期两个参数进行设置，本次实验数据设置了有效波高H=0.05 m，波浪有效周期Th=2.0 s，和有效波高H=0.1 m，波浪有效周期Th=3.0 s两组数据进行仿真，得到图2不同有效波高和波浪有效周期条件下波浪频率与JONSWAP幅度谱的关系图.

从图2(A)、(B)中可以得出有效波高对频谱的幅度值影响较大，有效波高从0.05 m增加到0.1 m，幅度峰值从0.000 57增加到0.001 3，有效波高的微小变化会对幅度谱的幅值产生较大改变，由于JONSWAP幅度谱的该特性，可以方便选取幅度参数值，可以对不同强度的波浪进行模拟，当有效波高值越大，海浪波动高度越高，海浪浪级越高.从图2(C)、(D)离散后的频谱图中可以得出，不同波浪周期对波浪频率长度的影响较大，波浪周期越大，波浪频谱宽度越小，所需采样点越少，计算海浪方程组的量减小，此时已经可以模拟出真实的海浪；相反，波浪周期越小，波浪频谱宽度越大，所需采样点越多，计算海浪方程组的量增加，此时模拟出的真实海浪高度细节降低.在仿真海浪时根据海浪需求进行频谱的选取以及采样点数量的选取.

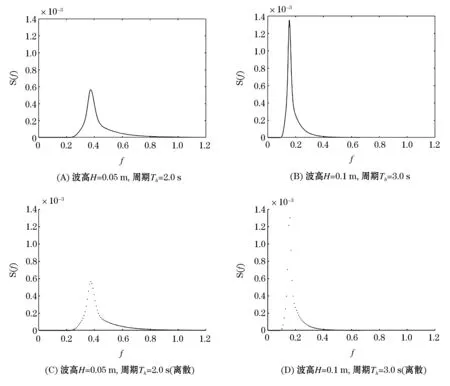
图2 不同有效波高和波浪周期的JONSWAP幅度谱Figure 2 JONSWAP amplitude spectrum of different effective wave height and wave period

2.2 海浪仿真

2.2.1 不同频谱下海浪仿真结果

在Visual Studio2010对海浪模型进行仿真，利用OpenGL进行数据处理，将数据利用数组进行存储，且将海浪几何模型利用三角形面绘制出来，仿真了网格的海浪表面.针对不同频谱提取出的参数进行仿真，仿真结果如图3所示，其中图3(A)表示有效波高H=0.05 m，波浪有效周期Th=2.0 s，取10个频率采样点时仿真得到的海浪图，其中图3(B)表示有效波高H=0.1 m，波浪有效周期Th=2.0 s，取15个频率采样点时仿真得到的海浪图，其中图3(C)、(D)分别表示有效波高H=0.15 m和H=0.2 m，波浪有效周期，取15个频率采样点时仿真得到的海浪图.

从图3中可以得出，随着有效波高的增加，仿真得到的海浪波强逐渐增加，从涟漪海面逐渐到有浪的海面，可以仿真模拟不同波浪强度的海浪背景图，从有效周期可以得出，周期的缩短和采样点数量的增加模拟出的海浪逼真程度更高，波浪强度越大，其体现出的逼真程度越明显，因此在海浪模拟中，可以根据实际需求进行参数设置.

图3 不同频谱参数海浪仿真图Figure 3 Wave simulation diagram with different spectrum parameters

2.2.2 不同海浪模拟方法仿真结果

本文在实验环境为cpu：Intel(R) Core(TM) i5-4210U，主频1.70GHz，内存4.0GB，操作系统Windows10下各种方法的仿真帧率如表1所示.不同海浪仿真方法仿真出来的海浪效果如图4所示，其中图4(A)、(B)表示几何模型模拟的海浪仿真图，图4(C)、(D)表示物理模型模拟的海浪仿真图，图4(E)、(F)表示本文方法模拟海浪的仿真图.

表1 不同方法的仿真帧率Table 1 Simulation frame rate of different methods

从图4模拟出的三种海浪仿真图中，可以得出，几何模型模拟的海浪图，网格结构比较单一，不能够体现出波浪翻涌时的随机性和多变性，适合于模拟风平浪静，没有波动的涟漪海面场景；物理模型模拟的海浪仿真图，细节结构比较多，波浪出现的随机性较强，能够很好的模拟出海浪的各种细节，但是不适合模拟平静海面，而且计算量比较大，每一个波形都需要进行计算，对设备要求较高，在仿真的实时性方面较弱；本文方法可以模拟出不同类型的海浪场景，从涟漪海面到汹涌的海浪，适用领域广泛，针对不同场景选择不同海浪谱进行仿真模拟，且本文方法不需要实时计算每个海浪波形，克服了物理模拟计算量大的问题，提高了海浪模拟的真实性、随机性、多变性、实时性，减少了海浪模拟的复杂度.

图4 不同模拟方法的海浪仿真图Figure 4 Wave simulation diagrams of different simulation methods

3 结 语

本文采用了三维方程建模方法，提出了将 Gerstner函数作为波浪模型与JONSWAP谱相结合的方法来实现动态的海浪建模.选取的方程组Gerstner函数能够描述海浪的细节和真实度，并将其扩展成三维方程组建立了真实场景情况下的海浪模型，采用了JONSWAP海浪谱的谱参数对海浪模型进行控制，实现了海浪模型的真实性、多变性、波浪强度可变性、随机性、实时性的海浪特性模拟.本文提出的方法能够仿真出不同波浪强度下逼真的海浪场景，适用领域广，具有较好的应用价值.