“数的运算”教学中学生数学思维能力的培养

王倩

摘 要 “数的运算”是数学教学的主要内容之一，在义务教育第一、二学段的数学内容中占有重要的地位。在“数的运算”教学中可以从运算方法探究中培养学生的迁移能力、分析能力和概括能力，从运算题组练习中培养学生的比较能力、综合分析能力和类推能力，从运算知识应用中培养学生算法的选择能力、建模能力和推理能力。

关键词 小学数学 数的运算 思维能力

数学是思维的体操，数学在培养人的思维能力方面有着其他学科不可替代的作用。数的运算是数学教学传统内容之一，在义务教育第一、二学段的数学内容中占有重要的地位，在数的运算教学中不仅可以发展学生的运算能力，还可以有效培养学生的数学思维能力。林崇德指出，思维能力主要包括数学概念、判断、推理等基本思维形式，以及比较、分类、概括、类比、归纳与演绎、分析与综合等思维方法。下面笔者结合自己的教学实践谈一谈如何在数的运算教学中培养小学生的数学思维能力。

一、在运算方法探究中培养学生数学思维能力

1.在运算方法探究中培养迁移能力

迁移是指学生将以前获得的知识、技能、经验和方法对新的学习情境中的知识与技能的获得、经验的积累和方法形成造成的影响。数学知识的特点之一是联系性紧密，前后数学学习内容保持着一定程度的连续性，学生在学习新的运算时，容易将已有的知识、经验和方法迁移到新的学习活动中来。如学生在学习整十数乘一位数口算20×3时，想到一位数乘一位数2×3=6，根据2×3的积得出20×3=60，这样的算法就是一种迁移，不仅如此，接下来会继续把这种算法再迁移到200×3等整百整十数乘一位数的口算中，最后总结出算法。再如在学习加法运算律时，当学生根据5+6=6+5、84+16=16+84、845+23=23+845这几个加法算式总结出加法交换律之后，学生会把相关的经验再迁移应用到乘法交换律的规律总结上。因此，学生在进行新知运算学习时，只要新的运算与旧有的运算在结构形式上有相似的地方，教师就不妨让学生尝试探究算法，学生经历自主尝试探究的过程就能较好地培养迁移能力。

2.在运算方法探究中培养分析能力

分析原本是将研究对象的整体分为各个部分，并分别加以考察的认识活动。在数的运算教学中可以结合适当的内容培养学生的分析能力。如学生在学习两位数乘一位数的笔算方法时，借助小棒把12×3进行分拆计算。学生结合小棒图，有的先算3捆一共有多少根，算式是10×3=30，再算3个2根是多少根，算式是2×3=6，然后把两次运算的结果加起来;有的学生则是先算3个2根是多少根，算式是2×3=6，再算3捆一共有多少根，算式是10×3=30，最后把两次运算的乘积相加。虽然对于两位数乘一位数的运算的先后顺序不同，但是都能够清楚地表达算式的算理。再如学习两位数除以一位数46÷2时，借助小棒图分一分，先分4捆，把4捆平均分成2份，每份是2捆也就是20根，算式是40÷2=20;再分6根，把6根平均分成2份，每份是3根，算式是6÷2=3，然后把两次分得的结果相加。也可以先分6根，平均每份是3根;再分4捆的，平均每份是2捆，也就是20根，然后再把两次分得的结果相加。学生在这个过程中就是把乘法的运算分析过程迁移到了除法的运算中来，而后教师引导学生把橫式分拆运算与竖式运算对应起来帮助学生理解总结竖式算法。教师引导学生针对算法过程进行分析，培养了学生的分析能力。

3.在运算方法探究中培养概括能力

概括是人脑在比较和抽象的基础上，把抽象出来的事物的共同本质特征综合起来，并推广到同类事物的过程。学生在学习数的运算的过程中，需要总结概括运算方法，如学习小数乘小数时，在例题中呈现了两个乘法算式3.8×3.2和1.15×3.2，学生根据小数乘整数的算法进行探究转化成整数乘法进行计算，从3.8×3.2转化成38×32这个乘法算式中发现每一个乘数都乘10了，所以得出的乘积就是原来积的100倍，要把现在的乘积除以100才能够得到原来算式的结果，所以在整数乘积中按照从右向左数出两位点上小数点，而后用同样的思考方式得出1.15×3.2的乘积，教师接着引导学生观察两个算式，提出问题：两个乘数的小数位数与积的小数位数有什么联系？小数乘法应该怎样运算？学生在教师的问题引导下对算法进行概括，學生经过讨论概括出小数乘法的运算方法：先按照整数乘法的运算方法进行运算，乘数中一共有几位小数，就从积的右边起数出几位点上小数点，学生在这样的算法探究过程中培养了概括能力。

二、在运算题组练习中培养学生数学思维能力

1.在运算题组练习中培养比较能力

比较是把多组事物放在一起辨别事物的相同属性或者寻找不同差异的思维过程。在数的运算练习中经常会出示几组算式，让学生进行比较，从题组中发现、总结运算规律。如学生在学习了三位数除以一位数的整数除法，在练习中就出现了算一算、比一比的一组练习，第一组：423÷3，423÷4，423÷6;第二组：672÷6，620÷6，602÷6。第一组的三个练习主要是让学生通过比较发现：（1）被除数相同，除数不同，商就不同，除数越大，商越小;反之，除数越小，商越大。（2）都是三位数除以一位数，如果被除数的最高位上的数字大于或等于除数，商就是三位数;反之，商就是两位数。第二组的三个练习主要让学生通过比较发现：（1）除数相同，被除数不同，被除数越大，商越大;被除数越小，商越小。（2）被除数的百位数字是除数的倍数，十位数字如果大于除数，商的中间就没有0;十位数字如果小于除数，商的中间就有0。如果十位数字是0，个位数字小于除数，商的十位数字和个位数字也都有0。通过这样的一组算式的比较，发现除法算式的特点以便于准确判断商，提高试商的速度和准确率，培养小学生的数学思维能力。

2.在运算题组练习中培养综合分析能力

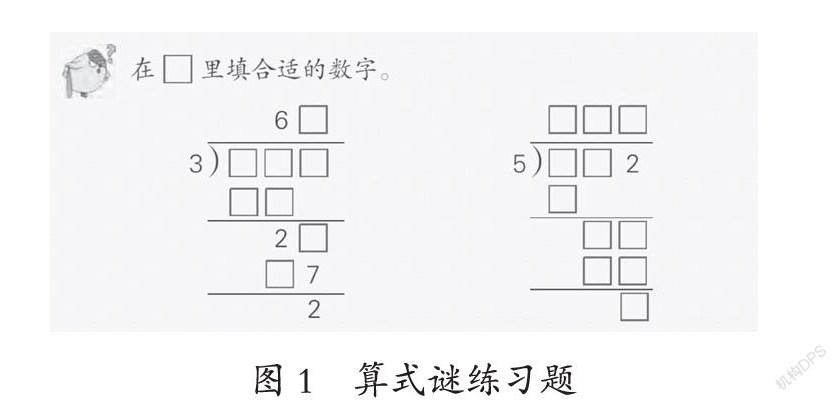
数的运算中有一类练习是算式谜，也叫虫食算，这类练习是一种含有一些字母、符号或有空缺数字的算式。算式谜因为数学思维含量比较高，难度比较大，所以一般都是出现在思考题中，在数的运算教学中呈现算式谜题组可以有效帮助学生提高综合分析算式的能力。如学生学习了两三位数除以一位数的除法之后，在复习中就出现了如图1的算式谜。教师引导学生学会分析：图1的第一个算式，根据商的十位数字6知道第一次与3的乘积是18，这样被除数的前两位数应该是18加2得20，然后从最后的差2是2□与□7相减得来的，可以推断出2□的个位数字9，那么这个被除数的个位数字也是9，□7的十位数字是2。

算式谜既包含除法的相关知识，又包含了乘法、加法和减法的相关知识，除此之外，更是注重学生对运算过程性学习的一种检测，通过算式谜这样的练习有效培养小学生综合应用知识有序分析的能力。

3.在运算题组练习中培养类推能力

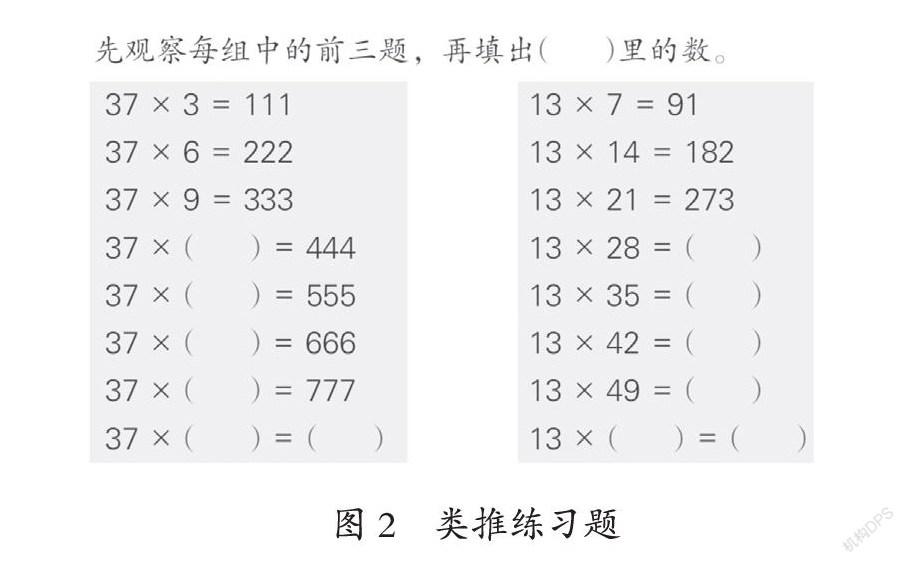
类推就是根据已有的一些事物的性质、特点、规律推理出和它同类的其他事物的性质、特点、规律。在数的运算中经常有这样的练习，先找出规律再直接写出后面算式的商，其本质上就是找出几个算式的共同特点以及内在规律，然后进行类推。从图2习题的第一组算式中发现它们的第一个乘数都是37，第二个乘数都是3的倍数，积都是111的倍数，这是算式的特点，找到了这些算式的特点后还要找算式之间的内在规律，如第二个乘数是3的几倍，积就是111的几倍，教师再引导学生进行深层次的总结：在乘法算式中，一个因数不变，另一个因数乘几，积也就乘几，总结出积的变化规律。当学生发现了算式的特点和内在规律后就可以继续进行类推，通过这样的题组练习，有效培养了小学生的类推能力。

三、在运算知识应用中培养学生数学思维能力

1.在运算知识应用中培养算法选择和灵活运用能力

灵活性是指思维活动的灵活程度，是学生在数学思维活动中，思考的方向、过程与思维技巧的即时转换水平的集中体现[1]。算法选择的灵活性就是根据问题解决的需要灵活选择算法进而快捷、正确解决问题。因为在实际解决问题中常常会用到多种算法解决问题，有的需要精算，有的可以口算，有的需要估算，有的还可以使用计算器进行运算，这就需要学生面对实际问题时能够根据问题中的数据信息以及所要解决的实际问题对算法进行灵活选用。如苏教版六年级下册第74页的一组问题：解答下面的问题，各适合口算、笔算、估算，还是使用计算器计算？先想一想，再解答。（1）一个阶梯教室有15排座位，每批20个，一共有多少个座位？（2）电影院楼下有698个座位，楼上有219个座位，这个电影院能够同时容纳1000人看电影吗？（3）在一个能容纳5万人的体育馆里，一场足球赛的上座率大约是75%，大约有多少人看了这场足球赛？（4）据第六次全国人口普查统计，上海市有2301.91万人，其中65周岁以上的约占10.1%，65周岁以上的有多少人？出示这组问题后，先让学生独立思考，然后个别交流，引导学生注意倾听准备评价。第一个问题，需要计算出具体个数，而且数目不是很大，因此口算就可以了;第二个问题是一个典型的估算问题;第三个问题需要进行笔算;第四个问题用计算器计算比较方便。当学生解答完这组题目之后，教师还要引导学生对问题进行比较，引导学生明确要根据题目的具体情况灵活选择算法，通过比较明晰各种算法的特点，以便于学生灵活选用。

2.在运算知识应用中培养算法模型的建立和解释能力

算法模型就是在运算过程中应该遵循的基本运算程序以及规律，混合运算中的乘加模型、三步混合运算模型等就是对运算程序和算法法则的一种模型建立。如整数乘法运算律的模型应用，当学生解答两步连乘问题“一部电视剧每天播放2集，每集35分钟，一共播放了15天。这部电视剧全长多少分钟？” 用这样的两种方法35×2×15或35×（2×15）時就是对乘法结合律模型的一种建立。再如学生解答行程类相遇问题“甲、乙两车同时从A、B两地相对开出，甲车每小时行驶86千米，乙车每小时行驶114千米，经过3小时两车相遇。A、B两地相距多少千米”用两种方法86×3+114×3和（86+114）×3时就是对乘法分配律模型的应用和解释。小学生在这样的运算应用中初步感悟建构、解释算法模型。

3.在运算知识应用中培养推理能力

小学数学运算多是渗透在问题解决中的，所以，问题解决中也往往伴随着学生推理能力的培养。一年级百以内的加减法的运算解决的多是一步运算的问题，而一步运算的问题多属于直接推理。如学生在解决一1班第一组有12名同学，其中有7名男生，女生有几人？因为题目中的两个条件是直接关联的，所以可以直接用12-7进行运算，在解释的时候，12是两个数的和，7是其中的一部分，求另一部分是多少，用减法。到了中年级的时候，学生学习了更多的运算，随之应用解决的问题难度也有所增加，最关键的是条件与问题不是直接关联，所以增加一步或两步，这样在数的运算应用解决问题就是属于间接推理，如学生学习两位数乘两位数之后，安排了两步连乘问题，在这样的运算应用中提升学生的间接推理能力，实现培养思维能力的目标。

总之，教师应该有目的、有计划地开展运算教学，使小学生的数学思维能力在数的运算的各个教学环节得到有效发展。

参考文献

[1] 林崇德.智力发展与数学学习[M].北京：中国轻工业出版社，2011：141.

[责任编辑：郭振玲]