基于“数”概念理解的数学实验开发

万兆荣

摘 要 数学学习是一种理解性学习，学习应当围绕概念的层阶化理解展开，教师要在技术工具上做好创造性的支持。以整数、分数、负数的认识为载体，开发验证型、探索型、理解型数学实验，为学生搭建数学思维支点或模型，引导学生建构“数”概念理解的框架，让静态内容动态化、系统化，进而促进深度学习的有效开展。

关键词 “数”概念理解 数学实验 验证性 探索性 理解性

“数”概念是人们在实践中，从数学对象的众多属性中概括、抽象出本质属性，其高度抽象性则是“数”概念教学的重点与难点。数学实验是以学生动手操作为支架的数学教与学的活动方式，通过实际操作，在认知与非认知因素参与下进行的一种发现数学结论、理解数学知识、验证数学结论的思维活动[1]。数学实验能够将“做、学、思”合一，让学生在猜想（或假设）、验证、归纳等活动中提炼出“数”概念产生的现实意义、文化背景和思想方法等，有利于学生对概念本质的探索和理解。

一、开发验证性数学实验，让“数”概念的理解可视化

验证性数学实验作为促进数学概念理解的一种具身认知工具，是基于自身经验对学习对象的起始性理解，让学生通过动手操作、观察模型、试验分析等手段，检验自己得出的数学结论（或猜想）的正确性的一种实践活动[2]。在“数”概念教学中，验证性实验可以使学生在物、图与数的对应关系中多感官参与活动，摆脱经验性理解的束缚，逐步向数学化符号表征转化，抽象出概念的本质属性。如“11～20的认识”教学难点在于怎样突破位值制和十进制，教学中可借助验证性实验，帮助学生突破学习难点。

本课可准备11个无序排列的蘑菇图、磁性小棒、长方形磁片等实验材料。实验步骤可以这样展开：第一步，猜想。出示数“11”，11为什么会写成这样，有其他写法吗？这里的两个1意思一样吗？第二步，验证。（1）圈11。要求学生用不同的方法圈数图片中蘑菇的数量，如一个一个圈、五个五个圈、十个一圈等方法。（2）摆11。要求学生用小棒拼摆出蘑菇的数量，方法有10个小棒摆一排，1个小棒单独放的;10个小棒捆在一起，1个小棒单独放……（3）写11。方法有：两个1中左边特别胖，右边特别瘦;左边写得高，右边写得矮;左边写得大，右边写得小……学生尝试用不同的方法表示10个1和1个1，即探讨“11”的表示，区别11中两个1的不同意义。第三步，归纳。任意选取（10+几）个长方形磁片，用十个十个圈数的方法，探究10个长方形磁片叠加表示十位上的1，这里的1放在哪里合适？通过位置关系证明十位上的1与个位上的1的区别。第四步，应用。继续利用长方形磁片在黑板上展示，学生自主增加磁片数量、确定摆放位置，表达对12～19的理解。

实验结果显示，通過数学实验活动，能够使学生在实验操作中发现知识生长的原点。学生最早对数的认识，正是其触摸、点数（shǔ）物体的动作经验的内化。学生从实验现象获得数的感性认识，再经过理性分析，对结论的真伪作出判断，这种差异性和多元性，充分反映了每位学生不同的已有经验和理解起点。从实验前对11的猜想到“圈”“摆”“写”，学生在实物直观的基础上理解十位上1的意义，经历经验性理解的修正、再创造过程，有效还原“11”原本的形态，充分获得体验“十进制”的经验。在理解“十进制”的数学原理、数学方法的基础上，学生逐步建立位次感、位值感，从工具操作的具象，到表象归纳，再到抽象的符号演绎，运用物、图、形等多元表征，对数的关键属性与本质的获得奠定基础。

二、开发探索性数学实验，让“数”概念的理解结构化

探索性数学实验是学生在教师设置的问题情境中，通过动手操作、观察、验证、类比、归纳等方式，发现全新数学结论的实践活动，特点是过程开放、探索性强、生成度高[3] 。在探究现实问题、揭示数学现象背后的数学原理、理解可推广的数学结论等方面，探索性数学实验发挥着重要的作用。如“分数的意义”教学中，分数具有“份数、商、测量运算以及比”等不同层次的意义，如何突破对整体的等分，体现分数的价值？这里，可以借助探索性数学实验重点突破两个学习难点：第一，整体等分，包括对具体“1”的等分以及许多合并成的整体的等分;第二，分数两种量的比较，也就是比的意义，所以分数在某种意义上来说也是比，它主要是两种量比较的时候，这两种量可以相互作为单位度量的意义，体现在应用当中。

本课准备的实验材料有两种大小不同的圆形纸片若干个，彩色笔、剪刀、粘胶。实验可以这样展开：第一步尝试画图表示分数。在1个圆形纸片中画图表示出 。要求学生独立操作后集体交流想法。第二步，再试。依次出示2个、3个、4个圆一组的图形，画图表示出一组图形的 。在学生独立操作后集体讨论不同方法并想办法验证。第三步，验证。借助剪刀现场剪下并展示在黑板上，理解多个圆片的  的表示方法。第四步，列表对比。出示多组圆的 ，讨论、归纳不同数量圆片用相同分数表示，并能从自然数1过渡到整体“1”，逐步理解单位“1”的喻意。

从实验结果可以看出：

首先，从“一个圆”开始，学生在等分的变化中感受分数中核心知识的整体性与关联性，进而加深对分数的理解。儿童早期在分割几何图形时采用的是“分半”的策略，并重复分半。因此，使用“偶数等分”认识分数，正是学生等分物体动作经验的内化。一个实验中学生要想得到圆片的  ，通常需要以两次对折的方式得到  ，这一活动顺应学生的认知过程，激活学生已有的知识经验，在等分的过程中直观感知部分与整体的关系，即其中的1份为  ，任意的3份为  ，在直观操作中感知一个圆的  的大小。同样，如果圆片的大小不同，其  的大小均是不同的，但是其中的1份都是  。这里，实物纸片均分实验使知识存在于具体的、情境性的、可感知的活动中，将抽象的分数概念具体化，使得学生的经验化理解逐步升华为数学的形式化理解。

其次，“多个圆”验证能够有效联结分数的多层意义。对2～4个圆片 的探讨，学生最易表示出4个圆片的  ，直接涂出3个即可;其次是2个圆的  ，第一种情况，有80%的学生将两个圆看成一个整体，平均分成4份，每半个圆表示1份，第二种情况，少数学生将2个圆分别看成一个独立的个体，将每个圆平均分成4份，分别表示出  ;对学生来说，将3个圆看作一个整体均分四份是最困难的，一个一个均分虽能达成目的，但比较复杂。那么，使用怎样的方式更加简单呢？学生通常是将3个圆叠加，累积成一个整体再均分4份。既含有3平均分成4份，又蕴含3除以4的除法意义，除法与分数意义的联结，促进学生多层级理解分数。

最后，列表分析归纳则有利于整体建构分数综合意义。列表对比将知识过程与结果、操作活动与思维参与、实验论证与主动探索有机融合，逐步从形式化向理解走向结构化理解。从1个圆到多个圆均看成一个整体，为整体建构分数意义提供了综合性载体。从现实情境过渡到数学意义上来，体现为一种逐步丰富、精细化的发展趋势，实现数学学习过程的可见。从自然数1过渡到整体“1”，两个“1”的变与不变融通建构单位“1”，一方面让学生感受被平均分对象的广泛意义，深刻体会分数部分与整体的含义，另一方面渗透集合均分思想，能够用“部分—整体”表示 的分数意义，实现了由实物走向模式的角色转换，逐步建立符号、模式、言语的联结。

三、开发理解性数学实验，让“数”概念的理解系统化

理解性数学实验是一种文化理解、外显知识的生成过程，为抽象架起直观理解的桥梁，使学生能从抽象的角度看待知识，理解数学问题产生的机理，根据数学问题的规律推测问题产生的变化，使得静态知识动态化、学术知识生长化。如“认识负数”是在学生认识了自然数、整数，初步认识分数和小数的基础上学习的。如何借助实验帮助学生理解负数的本质意义？笔者借助理解性实验展开教学。

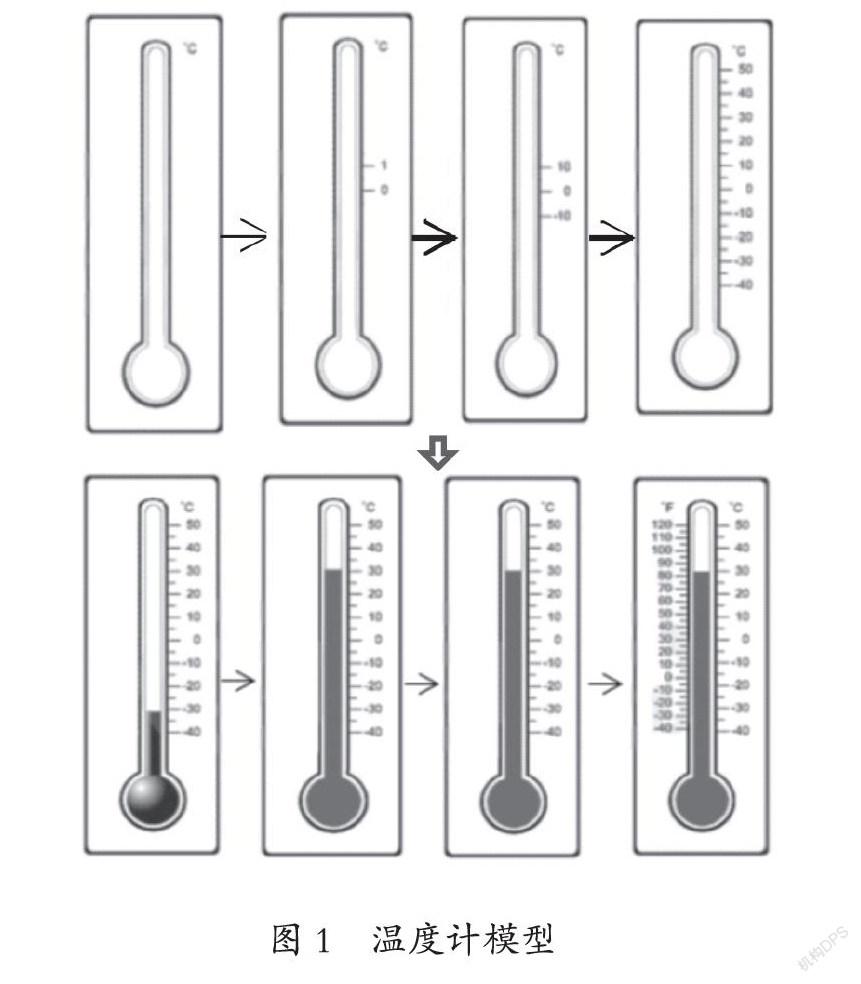
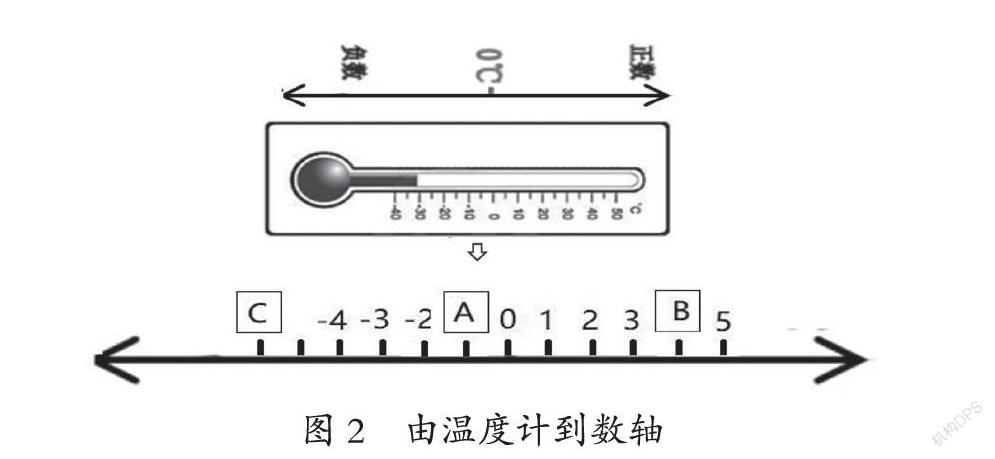
课前准备玻璃瓶、水、较粗的花茎、标签、温度计贴图、绘图笔等实验材料，并要求学生利用实验材料，通过插花看水位，发现起点、上升与下降的位置变化。第一步，猜想记录。由怎样记录水位变化引入新课，学生通过观察插花后水位向上和向下的相反方向移动想到，用0刻度作为原来水位的标准。第二步，画图验证。逐步完善温度计上的数字，继而聚焦知识结构难点，理解负数具有相反意义，并明确正负数的相互依存与相对性。从温度计模型上的无刻度到画出刻度，再到细分画刻度（如图1），在推理、概述中用现实原型概括出了负数模型。在探究体验和直观模型图的帮助下，掌握正负数在数系中的排列，深刻、准确地把握了概念的意义，体会正负数的相对性这一核心概念。第三步，应用推理。借助温度计方向变化，建立数轴意识，用数轴上的数“距”促进负数意义的相对性理解（如图2）。从实物抽象出核心元素，在线段上绘制刻度，使数轴形成完整样态，在确定的两个点之间进一步认识正负数。可以借助A、B、C三个字母所表示的数字来描述，如以字母A为观察点，描述C的相对位置;以字母B为观察点，描绘数字3和5的相对位置;以字母C为观察点，表述右边数据、推想左边数据，试想一下C左边会有多少个负数。实验中学生经历观察、质疑、推理、比较、抽象概括的认知全过程，深度理解负数的意义。

数学实验的开发，需要教师准确定位实验目标，明确知识之间具有什么样的數学抽象关系，将知识点和技能点穿插在实验中，并以任务为驱动，整合实验步骤，在完成任务的实验过程中让学生对所学知识进行意义建构。

参考文献

[1] 喻平，董林伟.初中数学实验的本质解析[J].课程·教材·教法，2016，36（08）：89-95.

[2] 齐雪林，王宁，赵仪娜.在《概率论与数理统计》课程中增加数学实验内容的探索与实践[J].高等数学研究， 2016，19（06）：55-60.

[3] 赵维坤，章建跃.初中数学实验的教学设计[J].课程·教材·教法，2016，36（08）：102-107.

[责任编辑：陈国庆]