机织物拆下纱线线密度测试方法的改进
梁 艳
(佛山市质量计量监督检测中心,广东 佛山 528000)
1 评价结果的测量不确定度
1.1 实验概述
本实验将试样调整在(20.0±2.0)℃,相对湿度为0.65%±0.04%的自然条件,根据GB/T 29256.5—2012的标准来操作实验品[1]。
1.2 数学模型
依据GB/T 292569.5—2012建立数学模型。

式中:T表示标准回潮率的纱线线密度,mD表示干燥纱线的品质;R表示纱线的公定回潮率,%;表示纱线的平均伸直长度,m;TR表示公定回潮率的纱线线密度,tex。
1.3 标准测量不确定度分量的评定
1.3.1 通过纱线平均伸直长度测量引入的不确定度成分
1.3.1.1 测量重复引入的不确定度分量u1()
(1)实验品:涤棉机织物。
(2)实验品数量:纬向样品5块,纬向纱线10根,选定伸直张力为6.56 cN,实际施加伸直张力为6.50 cN,得到试样纬向拆下纱线线密度测试数据,如表1所示,用统计方法评定A类标准不确定度。

表1 试样纬向拆下纱线线密度测试数据
1.3.1.2 由捻度仪伸长标尺示值引入的不确定度分量u2()不确定度U=0.2 mm(k=2),则
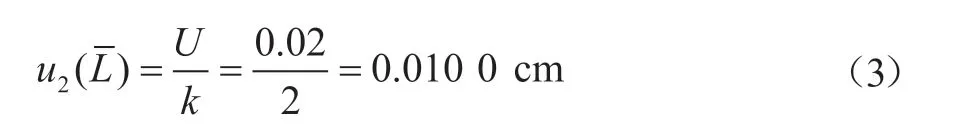
1.3.1.3 加捻仪拉尺示值所引入的不确定度分量u3()
纱的伸直长度L与所受张力F相关,通过下述实验得到数据拟合曲线,从而得出了两者的关系[2]。
由1条纱线,选择好相应的实验点,再施加张力5.00、6.00、6.50、8.00、10.00、6.50、8.00、10.00 cN,各自确定好6条纱线伸直长度。
1.3.1.4 引入不确定度分量u4()
实验中,ΔF=0.06 cN,假设其服从均匀分布,则

1.3.1.5 通过纱线平均伸直长度测量引入的不确定度分量u()
引入的不确定度分量如下式:

1.3.2 由纱线干燥质量测量引入的不确定度分量
1.3.2.1 测量重复引入的不确定度分量u1(mp)采用统计方法,对每一类样品的50根纱线干燥质量分别进行复测,用统计学方法评定A类标准不确定度。
1.3.2.2 纱线烘干质量测量引入的不确定度分量u(mp)
引入的标准不确定度分量为
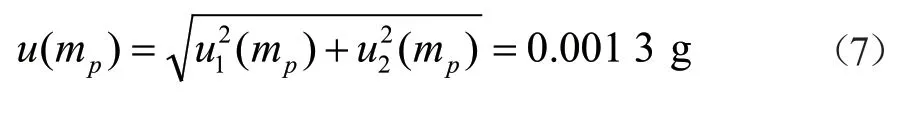
1.3.3 由公定回潮率引入的不确定度分量u1(R)
公定回潮率R利用下式计算:

在分布理想状态下,则

1.4 综合标准不确定度评估
在数学模型式(1)中,输入量mD、R,合成标准不确定度(T)如下式,可求出灵敏度系数。
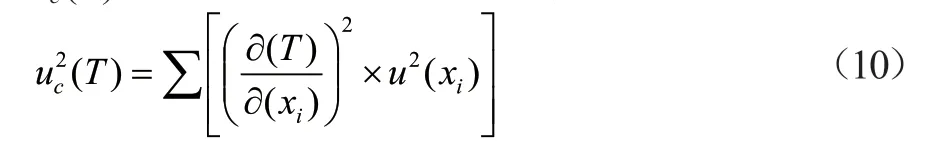
各组分的标准不确定度和灵敏度系数代入式(10),计算各组分的标准不确定度,得

1.5 标准扩展不确定度评价
当标准扩展不确定度评价k为2时

则U(TR)=12.98 tex。
2 结语
根据GB/T 29256.5—2012,对纱线线密度测试结果不确定度进行研究,样品的测试数量由10根减至5根。测试机织物拆下纱线线密度的方法,参考现有纱线标准GB/T 5324—2009、FZ/T 12013—2014等,中上一等品纱线线密度偏差均不低于±2.5%,对改进后方法的可靠性进行确认。结果表明,所有实验线密度测试数据的相对扩展不确定度为0.004 2~0.024 9。本研究采用的方法可以达到纱线标准需求,能提升机织物拆下纱线线密度的实验效率,大大节约了实验时间。

