资源约束与环境保护对经济增长的影响

杨 萍

（河南师范大学新联学院，河南 新乡 453000）

1 问题的提出

在工业化和现代化的过程中，尽管人们越来越重视资源和环境对经济增长的影响，但是在经典经济增长理论方面的研究，并没有突出资源和环境的作用。我们可以将目前在经济增长理论研究中对资源和环境的忽视总结为三个方面：

首先，在生产函数的构成要素中，资源并没有作为一个独立的生产要素被引入。尽管在个别学者的著作中，提出了包括能源在内的三要素生产函数，但并没有以此为基础进行深入的应用性理论研究。这是生产函数的一个缺陷。资源与资本是不同的，资源不可再生，特定时空条件下供给总是有限的，而且是逐步减少的；而资本可再生，资本可以自我积累并不断扩张，其问题总体来说是扩张的。因此，对生产函数进行正式的扩展是必要的。

其次，在生产函数方面对资源要素的忽视，使得在经济增长理论的研究中，并没有涉及到资源的影响。尽管自然资源与经济增长的关系的研究吸引了大批学者，但是在经济增长理论或者模型中却罕见资源的作用（在资源经济学中似乎资源对经济增长还有反作用，如著名的荷兰病）。经济增长理论中已经强调了资本、劳动、技术、人力资本的作用，但是资源却无从体现。另外，制度的作用也在理论中被抽象掉了。

最后，尽管现代人们越来越重视环境保护，也有很多学者研究环境保护和经济增长之间的关系，但是深入的理论研究，特别是在生产函数和经济增长的理论研究中，并没有给予足够的体现。比如传统的生产函数和经济增长理论并没有表明生产过程会产出污染。传统的GDP衡量的是每年新创造的价值，至于这些价值是否符合人们的需要，GDP创造中是否带来人们不喜欢的副产品，在生产函数和经济增长理论中，是没有体现的。

因此，本文试图从生产函数的视角，通过对传统生产函数的改造和扩展，并用之改造传统的新古典经济增长理论，使之能够突出和分析资源以及环境约束对经济增长的意义。

2 新生产函数的构建

2.1 规模报酬不变的生产函数

生产函数的基本定义是给定的技术条件下，要素投入和该要素投入所能产生的最大产出之间的函数关系，一般记为：

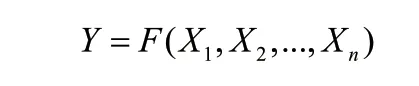
按照要素之间的可替代性，生产函数可以分为完全可替代（即要素之间的替代弹性为无穷大）生产函数和完全不可替代（要素替代弹性为零）生产函数以及其他生产函数。要素替代弹性介于零和无穷大的生产函数之中，有三种比较突出的常用生产函数：替代弹性为1的柯布－道格拉斯生产函数、不变替代弹性生产函数和可变替代弹性生产函数。一般来说，要素之间既不是完全可替代的，又不是完全不可替代的，要素之间替代弹性不是不变的，而是可变的。就具体应用来说，可变替代生产函数相对复杂。就不变替代弹性来说，在经济增长理论中应用最多则是替代弹性为1为C－D生产函数。就C－D生产函数而言，又可以分为规模报酬不变、增长和递减三种，本文使用规模报酬不变的生产函数。

2.2 投入生产要素的重新规定

就考虑的投入要素而言，传统经济增长理论中，一般考虑技术、资本和劳动三种投入要素。本文认为投入要素是复杂的，影响经济增长的因素也是复杂，因此，有必要对生产函数的投入要素进行扩展。首先我们加入自然资源这一生产要素。自然资源与资本不是同一种生产要素，自然资源具有特定时空条件下具有供给有限性和不可再生性，而资本则是具有供给弹性和可再生性，因此，就经济增长理论来说需要加入自然资源这一生产要素，记为E。土地也是一种重要的自然资源，考虑到模型的简单性，我们将自然资源与土地合并记为E。另外，能源也是一种重要生产要素，同样考虑到模型的简单性，将这合并进入E。也就是说本文的自然资源概念R包括了通常意义的自然资源、土地和能源三个内容。

技术主要表现为在投入要素数量和质量不变的情况，技术进步可以使要素的最大产出发生变化。在传统的生产函数中，广义技术进步包括管理创新等所有非要素投入数量和质量变化而带来的产出增加，我们将管理创新这个要素单列出来，并将之推广为制度因素。在技术水平不变和要素投入数量、质量不变的条件下，制度安排的变化，可以对主体行为产生新的激励和约束，因此，可以改变产出。诺思（1968）指出，即在没有技术变化的情况下，制度变迁也能带来生产效率的提高，并引起经济增长。制度经济学家基本上都同意，制度对于经济增长是至关重要的。但是在经济增长的经典理论模型中，看不出制度的作用以及制度是如何对经济增长起作用的。因此，在经济增长理论中必须考虑制度因素，甚至，根据制度经济学家的观点，制度对于技术进步也是重要的。记技术要素为T，制度要素为O。

2.3 生产函数的重新设定

综上所述，本文生产函数考虑的生产要素包括资源E、资本K、劳动L、技术T、制度O，故而生产函数的具体形式设定如下：

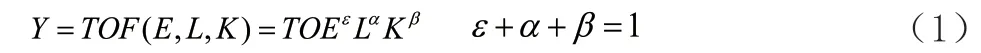
其中T和O没有加上上标，这是因为T和O都通过影响其他生产要素来提高产出的，其本身并不直接构成产出，而且技术和制度又可以相互影响，所以二者性质相近，故而将二者直接相乘并没有加上上标。其他要素的上标均表示各自的产出弹性。

需要注意的是，由于研究目的的需要，本文将在这里的生产函数设定的基本思想上，灵活对生产函数进行微调，具体的调整思路和方法，将在下文相应的部分给予说明。

3 资源和环境对经济增长的约束

3.1 经济增长因素的分解

对于式（1）两端用全微分展开可以得到：

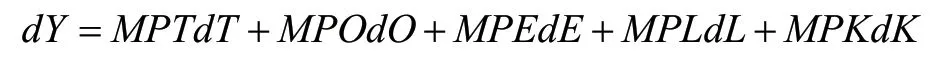
上式简化可以得到：

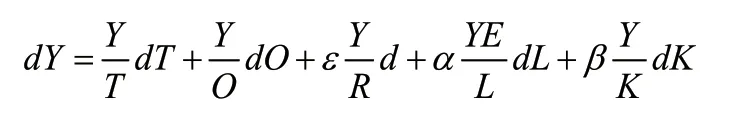
将上式两边都除以Y并整理可以得到：

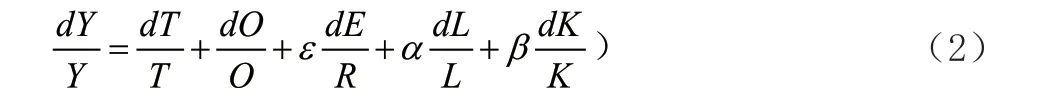
由上式我们可以看出，左边表示经济总是增长率，右边分别是技术变化率、制度变迁率、土地投入变化率、资源投入变化率、劳动投入变化率和资本投入变化率，各自系数表示相应的产出弹性，技术和制度的产出弹性为1。由于制度变迁率是无法准确衡量的，这个表达式也无法准确表明制度是正向改进还是负向退化，这里只是一个意义表征。近似来说，式（2）是一种模糊的经济增长分解表达式。

在（2）式中我们已经初步可以看出资源对经济增长的意义。如果土地和资源的投入无法增加，那经济增长的速度将受到很大影响。这似乎与经验事实不符合。事实，对世界各国来说，即使本国的土地和资源受到了供给约束，也可以通过国际贸易从其他国家获得土地和资源。从本质的角度来说，人类发展的历史，即是一部战争史，而战争只是为了获得土地和资源。近代以来两次世界大战，都是土地和资源对经济增长约束的真实写照。而美国70年代到80年代的滞胀也是经济增长资源约束的一个反映。但是（2）式还比较粗糙，因为它没有考虑要素之间是相互影响的，它们作为一个共同体投入生产过程中，（2）式并没反映这种关系。

3.2 资源约束对经济增长的影响

在这一小节，我们考虑投入要素之间在生产过程中相互制约关系，各投入要素必须以一定比例关系投入生产过程，这个比例关系可以在一定范围变化，但这个变化又有一定的极限。因此考虑单位资本资源密度、单位劳动资源密度、单位技术资源密度和单位制度资源密度。由于技术和制度单位衡量的困难，假定不考虑技术和制度变化，由于每种产品生产过程的特性，那么，每一个资源密度指标都有一个最小和最大的变化范围规定：

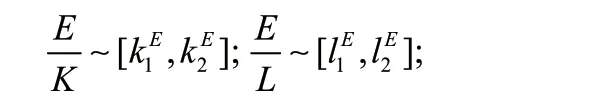
由于在特定的时空中资源供给本身是有限的，从宏观意义上来讲在特定时空投入生产中的资源也是有限的，因此，令：

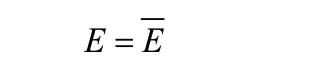
则上式变化为：

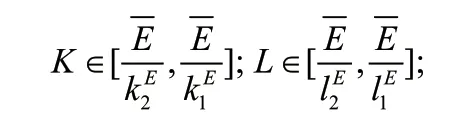
如果技术水平和制度结构保持不变，那么，社会可用的总自然资源和能够投入到某产业和自然资源总是有限的，如果资源利用达到了瓶颈，那么，这将锁定资本和劳动要素的有效投入量。所谓有效投入量，即是指该要素投入的边际产量为正时的投入量。此时，即使其他生产要素依然丰富，经济增长也会陷入停滞。这就是经济增长的资源约束。考虑到资源资本比和资源劳动比仅在特定的范围之内变化，我们可以假设这个范围非常小，近似于固定，所以令：

（2）式可做如下变化：

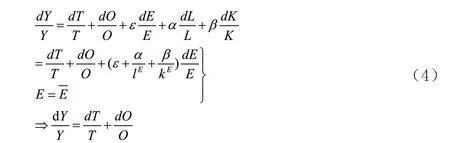
由式（4）可以看出，尽管e、l、k可以在一定范围内变化，但是如果R在给定时空内达到了极限，那么上式右边的第三项整体将为零。此时，经济增长只能依靠技术进步和制度创新。

3.3 环境对经济增长的约束

到现在为止我们并没有考虑产出的类型。根据生产函数（1）或者生产函数式（3）我们默认生产出来的东西，都是适合社会需要的财富。而我们经济增长的核算中，所核算的对象GDP只是表示新创造出来的价值，不但没有核算创造这些GDP的代价，也没有核算创造这些价值有多少是适合人们需求的，有多少是对人类有害的。这正是传统研究的不足之处。

我们把最适合或最能满足人们需求的创造出来GDP称为有效GDP，记为EY。比如生产出来的劣质香烟，尽管也能吸，但显然不是有效GDP。我们将那些创造出来的不属于最适合人们的需求的价值称为非合意GDP，记为SY。在现实生活中，我们投入生产要素生产出来的东西，除了正常的产品，还经常产生一些副产品，如废水、废气、废渣、灰尘、噪音、射线等，我们称这些产品为坏的GDP，记为NY。如果新创造出来的产品的价值，超过经济体系中社会有效需求时，这些创新创造的产品为过剩产品，我们记为XY。所以，式（1）可以变化为：

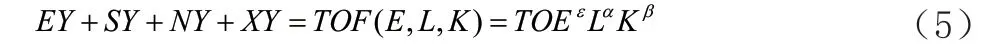
根据上式我们对式（4）进行扩展就可以得到一个有效GDP增长率表达式：

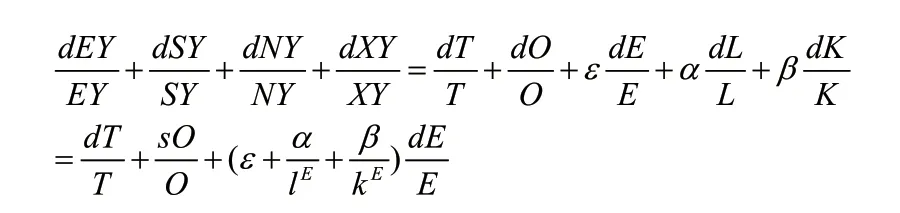
将上式左边除第一项外其余项都移动到右边可以得到：

式（6）中的小字母g分别表示相应的增长率。

我们通过式（6）可以看出，有效经济增长率取决很多因素，不能认为要素投入增加、技术和制度创新就一定能够实现有效经济增长。更为重要的意义是，我们强调有效经济增长的概念，从产出的角度强调次优产出、负面产出（环境污染等）和过剩产出对资源的浪费和对经济增长本身的伤害。

4 资源和环境对稳态经济增长的影响

4.1 经济增长率的性质和新生产函数的设定

1.经济增长的最优性。实际上式（2）、（4）、（6）只是告诉我们，如果经济增长了，那么是哪些因素导致了经济增长。如果我们想保持经济持续增长，我们需要做些什么。但是这些式子并没有告诉我们这样的一个经济增长率是否适合，也不能告诉我们政府为保持经济增长应该做些什么。我们可以将这式（2）、（4）、（6）表示的经济增长率称为实际增长率，它可能过高、过低或者适中。

其次，我们在推导式（2）等时，也没有考虑到需求问题，只是从生产的角度做了研究。因此，我们需要对它们进行完善。那么，什么才是最优的经济增长率呢？一个基本标准是这样的经济增长率下，所生产出来的产品供给正好等于产品的需求[1]。尽管GDP衡量是的新创造的产品的价值，但是如果这些价值不是社会所需求的，即使经济在增长，但社会福利并没有增加，社会资源却在浪费。

最后，根据生产函数（1）式保持规模报酬不变的假设，另外，由于本文并不着重研究制度因素，而且制度因素与技术因素作用基本相似，为了研究方便，用符号A重写技术，而且加入制度因素，因此，可以将（1）式写为人均产出形式：

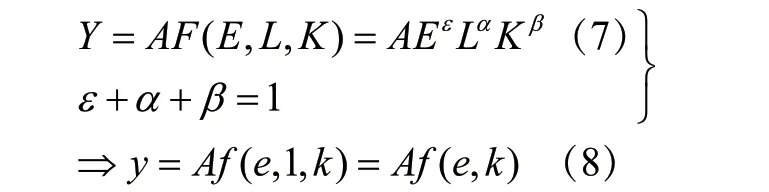
生产函数（7）式和（8）式并无新意，而且很多学者已经将之创造出来，本文只是试图将之运用于经济增长理论的研究中。

4.2 人均资本积累方程

4.2.1 不考虑资源考虑政府因素的资本积累方程

令s表示储蓄率，根据式（7）可以得到总储蓄表达式：

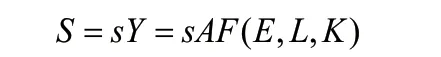
又设政府税收为：

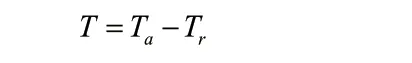
即政府的税收减去转移支付，由此产品市场供给可表示为：

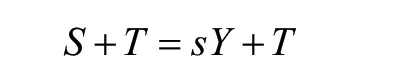
设政府社会总投资为I，政府购买为G，因此总需求可表示：

那么，我们可以将产品市场的均衡表示为：

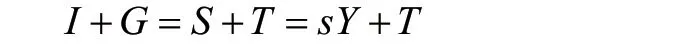
可以得到总投资的表达式：

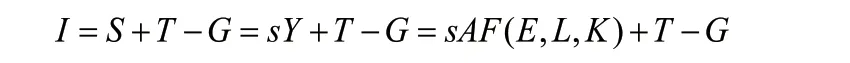
设总资本折旧率为σ，则每年资本的变化可以表示为：

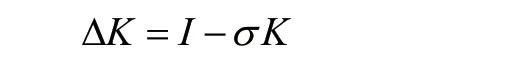
根据总投资表达式，可以得到社会总资本积累方程：

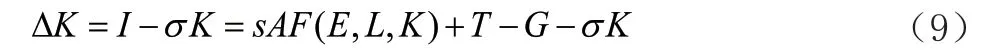
4.2.2 同时考虑资源和政府因素的资本积累方程

式（9）是传统的写法，只是加入了需要政府因素。现在我们考虑资源因素。企业每年的投资，一部分购买资产形成资本，另一部分购买资源并消耗掉，其价值转移到新产品去，类似于原材料，但是与原材料又不同。原材料也是一次性消耗掉，而且其价值转移到了新产品中，但是特定类型的原材料只能生产特定类型的产品，而资源比如煤、石油及电力，是生产任何产品都要消耗的。为了考查能源的影响，所以对（9）式作一改造，加入资源消耗：

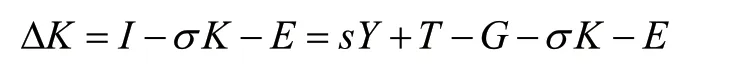
那么，总资本变化率方程为：

4.2.3.人均资本积累率方程

所谓人均资本积累率，是指人均资本随着时间变化而变化的量与原人均资本量的比率，在这一部分，我们用小写的k来表示人均资本，则人均资本变化率方程为：

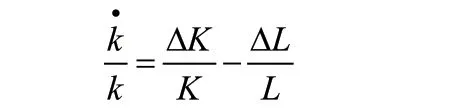
根据（10）式，人均本积累率方程变化为：

令人口增长率为n，我们将上式继续变化为：

其中的t、g、ε分别为人均单位资本政府净税收、人均单位资本政府购买和人均单位资本资源消耗，人均资本积累方程为：

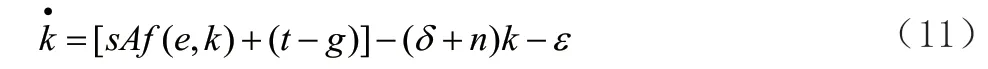
上式的人均资本积累方程与新古典经济增长模型中人均资本积累方程大同小异，只不过这里面是希克斯技术进步，而且在方程里加入了人均资源变量ε、政府净收入变量（t-g）。

4.3 资源约束对稳态均衡的影响

所谓的稳态是人均产出增长率为零，即每年的人均产出都保持不变的状态。为了达到这个条件，我们观察人均生产函数（8），则要求人均资源e和人均资本k每年保持不变。对于人均资本k每年保持不变来说，意味着人均资本积累为零，即

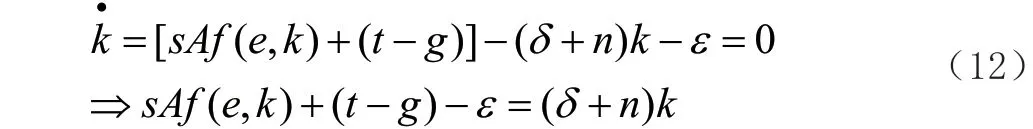
(n+δ)k如果（12）式得以满足，那么就意味着每人均资本不变，但这并不意味着人均产出不变，因为，决定人均产出水平的，还是人均资源水平e。我们可以将上式作图于二维坐标轴上：

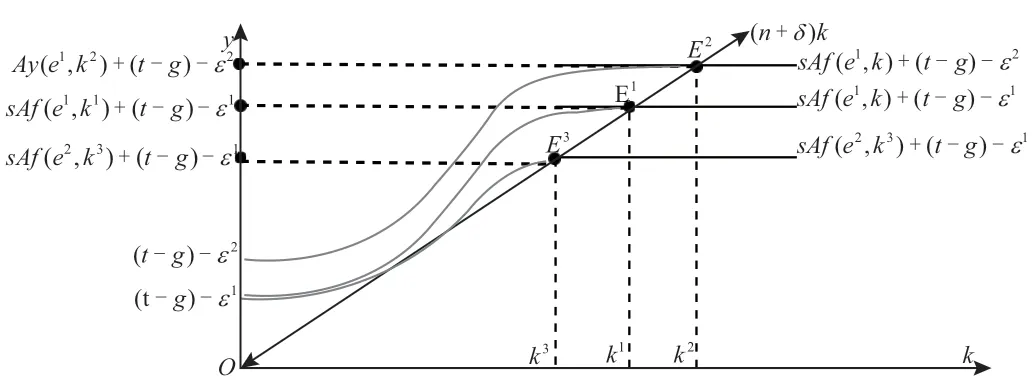
首先，假设模型原来的均衡点为E1点，对应的均衡人均资本量为k1，此时的人均单位资本资源密度为ε1。如果ε变小下降为ε2，意味着同样的劳动和资本投入，所消耗的资源或者能源变小了，这说明资源更为高效的利用，因此，在其他条件不变的情况下，从图上看，均衡点变为了E2，k增到了k2，结果人均产出得以增长。这是资源利用效率的提高。

其次，从另一个角度来讲，人类社会的自然资源和能源储量是有限的，现代经济增长越来越受到资源和能源的约束，在资源利用效率ε不变的情况下，国家能够利用的资源会减少，即e减少。如上图所示，原来均衡点为E1。现在资源投入不足，导致原来生产曲线的斜率下降，新的均衡点为E3，结果人均资本受此影响降为了k3，人均产出随之下降。这就是资源对经济增长的影响。

最后，上述模型还从经济增长的角度重新审视了政府的宏观经济政策，特别是财政政策。T实际上政府储蓄，g是政府支出，从图上看，在其他条件不变时，要想保持长期的经济增长，政府实行紧缩性财政政策似乎是有必要的。或者，最好实行平衡的财政政策，长期内对经济增长就没有影响。之所以从图上看不到货币政策的影响，是因为我们没有考虑货币因素[2]。

4.4 环境污染对经济增长的影响

我们现在假定，不考虑其他因素，如资源约束、政府政策等，现在来考虑产出，对经济增长的影响。根据（5）左边我们对产出分为四类：有效产出EY，次优产出SY，负面产出（环境污染等）NY，过剩产出XY。那么相应的人均产出分别表示为：yE、yS、yN、yX；那么，根据式（12）然后做相应整理变换我们可以得到稳态的条件：

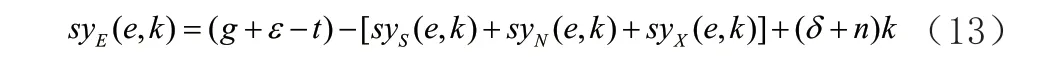
将式（13）画在以k作为横坐标的二维坐标轴上我们可以得到下图：

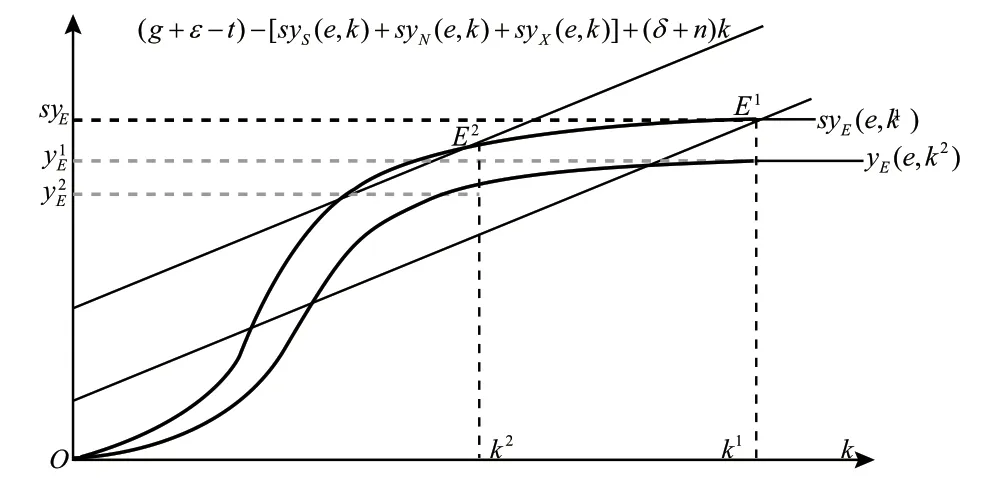
如上图所示，原来的稳态均衡点为E1点，均衡的有效人均产出为yE1，对应的人均资本水平为k1。现在假设资本、资源、技术、制度等的投入都不发生变化，只是国家创造了更多环境污染、过剩产品。由上图我们可以看出，其中的直线曲线将向上平移，结果将导致一个更小的人均资本水平k2，在均衡点E2处，对应着更小的人均产出和有效人均产出yE2。这正反映了环境对经济增长的约束。

5 研究结论

本文利用扩展的生产函数，即加入了新的生产要素，包括技术、制度、土地、资源、劳动、资本，构建了一个新的生产函数。并以这个新的生产函数为基础，首先对经济增长的基本因素进行了分解，从而分析了资源约束和环境约束对经济增长的影响。同时，本文还利用新古典经济增长模型，并对之进行扩展来分析资源约束和环境约束对经济增长实现稳态均衡时的影响。本文的这两个模型可以在一定程度上体现资源、环境、技术和制度对经济增长至关重要的作用，从而为实证研究打下了经济理论基础。