Dynamic response of bilayered saturated porous media based on fractional thermoelastic theory#*

Min-jie WEN, Kui-hua WANG, Wen-bing WU, Yun-peng ZHANG, Hou-ren XIONG

Dynamic response of bilayered saturated porous media based on fractional thermoelastic theory#*

Min-jie WEN†1,2, Kui-hua WANG1,2, Wen-bing WU3, Yun-peng ZHANG3, Hou-ren XIONG4

Research Center of Coastal Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China Engineering Research Centre of Rock-Soil Drilling & Excavation and Protection, Ministry of Education, Faculty of Engineering, China University of Geosciences, Wuhan 430074, China †E-mail: 0620577@zju.edu.cn

Considering the thermal contact resistance and elastic wave impedance at the interface, in this paper we theoretically investigate the thermo-hydro-mechanical (THM) coupling dynamic response of bilayered saturated porous media.Fractional thermoelastic theory is applied to porous media with imperfect thermal and mechanical contact.The analytical solutions of the dynamic response of the bilayered saturated porous media are obtained in frequency domain.Furthermore, the effects of fractional derivative parameters and thermal contact resistance on the dynamic response of such media are systematically discussed.Results show that the effects of fractional derivative parameters on the dynamic response of bilayered saturated porous media are related to the thermal contact resistance at the interface.With increasing thermal contact resistance, the displacement, pore water pressure, and stress decrease gradually.

Bilayered saturated porous media; Thermo-hydro-mechanical (THM) coupling dynamic response; Fractional thermoelastic theory; Thermal contact resistance; Elastic wave impedance

1 Introduction

The thermo-hydro-mechanical (THM) coupling theory of porous media is of great importance in civil and energy engineering (Mei and Yin, 2008, Li CX et al., 2010, 2012, 2017, 2020; Li and Xie, 2013; Mei and Chen, 2013; Zhang et al., 2021).Numerous practical projects, such as extraction of geothermal energy, storage of thermal fluids, and deep geological disposal of radioactive waste, need to carry out THM coupling analysis before construction (Levy et al., 1995; Liu et al., 2010b; Tao et al., 2014).Therefore, considering the neglect of fluid flux in the thermoelasticity, a detailed and in-depth understanding of hydrothermal, hydromechanical, and thermo-mechanical processes is necessary for describing the coupling behavior of fluid-saturated media (Liu et al., 2009).To overcome the shortcomings of the classical uncoupled and coupled thermoelastic theory which assumes the thermal wave propagates at infinite velocity (Biot, 1956; Booker and Savvidou, 1984; Wang et al., 2013; Zhang et al., 2022), generalized thermoelastic theory and diffusions theory have been proposed (Lord and Shulman, 1967; Green and Lindsay, 1972; Abbas and Marin, 2018; Abbas et al., 2019).

Many studies based on the above theories have been applied to specific cases.Sherief and Hussein (2012) developed a THM coupling mathematical model with two temperatures for porous media, and analyzed the transient response of semi-infinite thermoelastic media subjected to thermal impact.Liu et al.(2010a) investigated the thermo-viscoelastic dynamic response of saturated porous media.Lu et al.(2010) focused on the dynamic thermo-mechanical response of half-space saturated poroelastic media and summarized the differences in response between thermoelastic and saturated porous thermoelastic media.Xue et al.(2020) studied the coupled thermal-moisture response of a cylinder with circular cracks and determined the effect of relaxation time on the response.Based on the two-temperature theory, Hussein (2018) theoretically investigated the effect of porosity on the temperature increment, displacement, and pore water pressure of solids and fluids.Singh (2013) used the generalized thermoelastic model to analyze the propagation and attenuation characteristics of elastic waves in saturated porous thermoelastic media.Saeed et al.(2020) investigated the dynamic thermoelastic response of saturated porous materials by finite element method.Youssef(2007) adjusted the generalized thermoelastic theory based on the Lord-Shulman (L-S) thermoelastic model.Bhatti et al.(2020) presented a theoretical study on the swimming of migratory gyrotactic microorganisms in a non-Newtonian blood-based nanofluid via an anisotropically narrowing artery.Khan et al.(2019) examined a third-grade magnetohydrodynamic fluid with variable thermal conductivity and chemical reaction over an exponentially stretched surface.Alzahrani and Abbas (2020) used finite element method to investigate the generalized thermoelastic response of saturated porous materials.

Note that all the above-mentioned solutions neglect the different heat conduction phenomena in the process of thermal wave propagation, and the temperature field of saturated porous media cannot be described by the generalized thermoelastic theory at high temperatures.To address this problem, Sherief et al.(2010) and Sherief and El-Latief (2015) derived an equation of generalized thermoelasticity with a fractional derivative, and Youssef (2010) proposed a damped version of Fourier’s law using time-fractional derivative theory.Subsequently, some researchers used fractional thermoelastic theory to investigate the dynamic response of saturated porous media or thermoelastic media.Ezzatet al.(2015) introduced a heat conduction model with a fractional derivative to investigate the dynamic response of half-space porous media.Based on fractional thermoelastic theory, Sherief and El-Latief (2013) derived a semi-analytical solution to the temperature-dependent heat conduction coefficient.Deswal and Kalkal (2013) analyzed the thermo-viscoelastic behavior of fractional micropolar media based on the two-temperature theory.Hussein (2015) focused on the fractional thermoelastic problem of an infinite cylinder and investigated the effects of fractional derivative parameters on the response.Sherief and El-Latief (2015) analyzed the fractional thermoelastic problem of thermoelastic media with a spherical cavity.Hobiny and Abbas (2021) established a bio-heat model with a fractional derivative to study the variations of temperature and thermal damage in spherical tissues during thermal therapy.In addition, Hobiny and Abbas (2020) proposed a mathematical model based on Green-Naghdi photothermal theory of fractional-order heat transfer to study wave propagation in a 2D semiconductor material.Considering the temperature-dependent characteristics of materials, Peng et al.(2020) studied the fractional thermal diffusion problem in infinite thermoelastic media with a spherical cavity.Alzahrani et al.(2020) investigated the behavior of a 2D porous material under weak, strong, and normal conductivity using the eigenvalues method.By introducing a time fractional derivative of the Taylor-Riemann series into the heat conduction equation, Wen et al.(2020) investigated the dynamic response of a circular tunnel in saturated porous thermoelastic media.

Differences among thermophysical parameters of each layer have a great influence on the distribution of physical fields in saturated porous media.Ai and Wang (2015a) focused on the axisymmetric thermal consolidation of layered saturated porous media due to a heat source.They investigated the 3D THM coupling response of saturated porous thermoelastic media (Ai and Wang, 2016).Ai et al.(2018)laid emphasis on the axisymmetric thermal consolidation problem of layered transversely isotropic soil and studied the effects of transversely isotopic parameters on the displacement, temperature, pore water pressure, and stress of soil.Wang and Wang (2020) investigated the long-term thermal consolidation properties of layered saturated soft soil and derived a semi-analytical solution of a saturated soft soil foundation under different rheological models via Laplace and Hankel transform.Considering the thermal diffusion effect, Ai and Wang (2015b) studied the 3D thermo-mechanical coupling response of layered saturated porous media.In the above studies, the interface of layered saturated porous media was simplified as perfect contact, and the effect of thermal contact resistance was ignored.

Due to microscopic unevenness at the interface, the interaction between two interfaces generally occurs at discrete contact points.When heat flux passes through the first layer of media, the area of the contact surface shrinks, resulting in a reduction of heat and the formation of thermal contact resistance (Fig.1) (Kek-Kiong and Sadhal, 1992).It has been reported that the thermal contact resistance is generated by the coupling effect of three factors, i.e.heat, force, and material, and is also affected by the surface roughness and material properties of the contact media (Yovanovich, 2005).Carr and March (2018) developed four different thermal contact resistance models for layered thermoelastic media.Xueet al.(2016) constructed an incomplete interface contact model and investigated the thermo-mechanical coupling response of a bilayer media based on the generalized fractional thermoelastic model.In another study, Xueet al.(2017)furtherintroduced a heat diffusion effect to analyze the transient response of multi-layer structures in the presence of thermal contact resistance.In a subsequent study, they explored the transient response of layered thermoelastic media with temperature-dependent thermal diffusivity and heat conductivity (Xue et al., 2019).LiCL et al.(2020)employed generalized thermo-viscoelastic fractional strain theory to investigate the thermo-mechanical response of a layered viscoelastic composite structure interface under non-ideal contact.Yuan et al.(2021) correlated the thermo-physical properties of a material with temperature and investigated the nonlocal thermodynamic response of an external thermal insulation system.He et al.(2019) analyzed the transient response of a spherical shell embedded in an infinite thermoelastic media based on a memory-dependent generalized thermoelastic theory.

In this paper, thermal contact resistance and elastic wave impedance are considered to simulate the imperfect conditions at the interface of a bilayered saturated porous media.The fractional derivative theory of thermoelasticity is introduced to describe the thermodynamic behavior of a bilayered saturated porous media.The analytical solutions of the dynamic response of the bilayered saturated porous media are derived by applying the operator decomposition method.Using the derived solutions, the effects of the fractional derivative parameters and thermal contact resistance on the dynamic response of bilayered saturated porous media are discussed in detail.

Fig.1 Thermal contact resistance model

1represents the heat flux

2 Problem formulation and governing equations

A schematic of a bilayered saturated porous media composed of two kinds of isotropic and homogeneous saturated porous media with different properties is shown in Fig.2.The first layer is marked by 1 and the second layer by 2.The upper part of the saturated porous media is subjected to a uniform harmonic temperature load0eiωt, where the angular frequency is denoted byand the temperature constant by0.i denotes a complex number, i2=−1, e the exponential function, andthe time.The model does not incorporate any external force or free drainage boundaries.The saturated porous media 1 and 2 are not in complete contact because of the presence of tiny pores.Moreover, the pores contain a small amount of water.The thermal impedance and the reflection and transmission propagation characteristics of elastic waves at the interface between the two layers (=) are taken into consideration, whereis the thickness of the first layer andis the coordinate of an origin at top surface (Fig.2).The lower part of medium 2 is infinite, i.e.it satisfies the condition→∞.Both the pore water pressure and displacement are fixed at 0, and the temperature remains unchanged.

As shown in Fig.2, the corresponding boundary conditions are derived as:

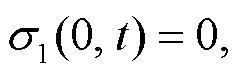
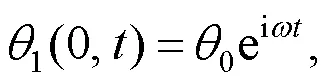
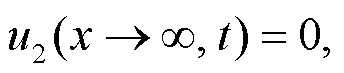
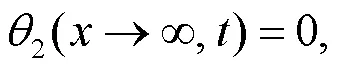
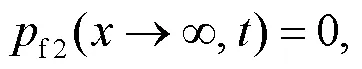
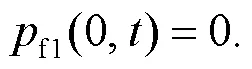
The interfacial conditions (Xue et al., 2016) are introduced as:

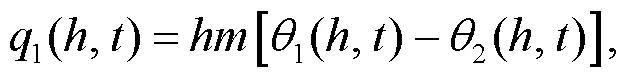
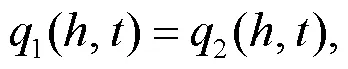
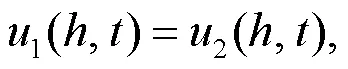
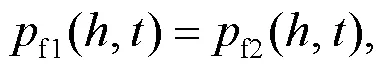
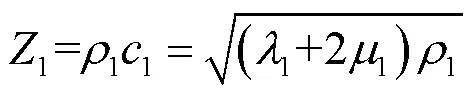
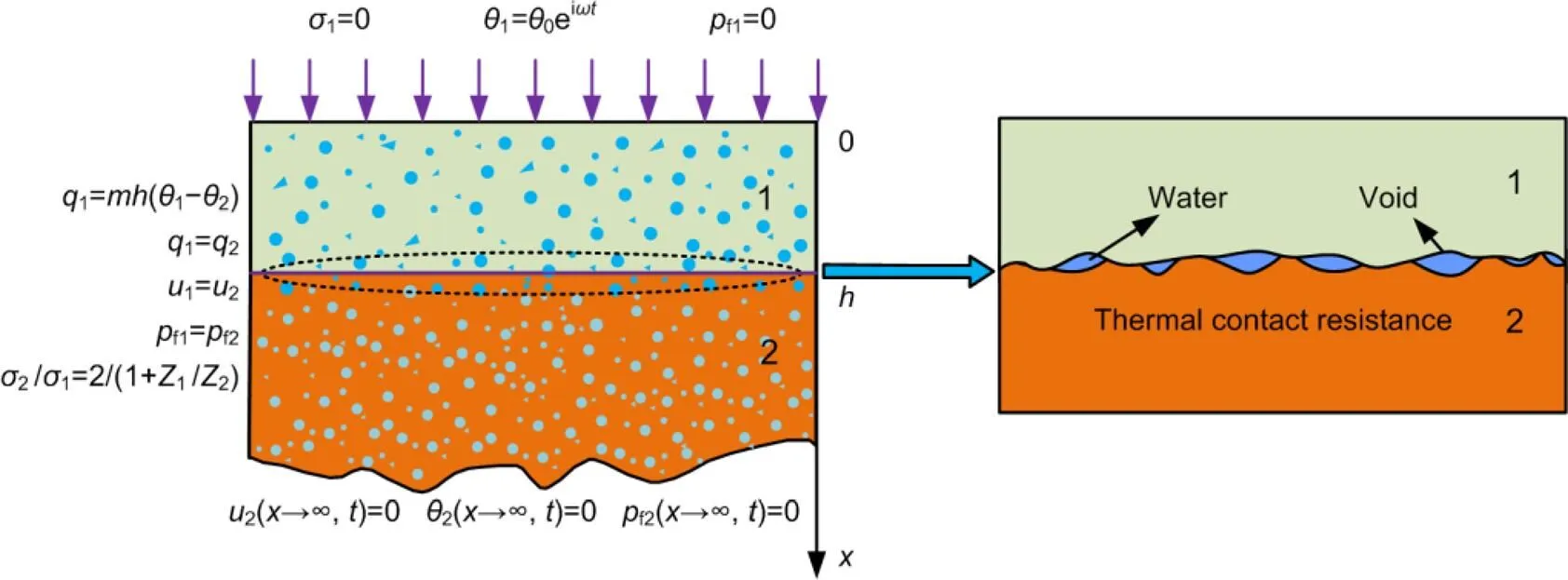
Fig.2 Schematic of the bilayered saturated porous media

Ezzat et al.(2015) proposed a fractional derivative heat conduction equation:

whereαdenotes the fractional derivative parameter,τdenotes the relaxation time, andkdenotes the heat conduction coefficient.

The governing equation for temperature is given as:

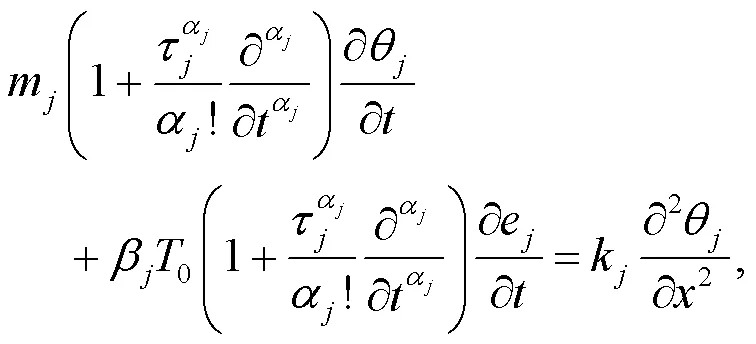
whereβ=(3λ+2μ)sjdenotes the thermoelastic modulus;sjrepresents the linear thermal expansion coefficient of solid grains;m=nρfjfj+(1−n)sjsjis the volumetric heat capacity of the media in whichfjandsjare the specific heat at constant strain of pore water and solid grains, respectively;e=∂u/is the volumetric strain.As shown in Fig.2, by neglecting the inertial effect and body force of the fluid, the motion equation of the bilayered saturated porous media can be written as (Lu et al., 2010):

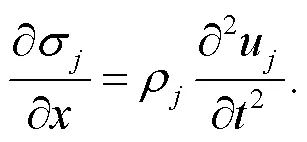
The constitutive relation can be written as (Ai and Wang, 2015a):

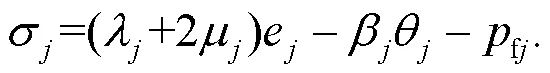
According to Darcy’s law, the fluid motion equation can be expressed as (Luet al., 2010):

whereb=fj/dj;is the gravitational acceleration;djis the permeability coefficient of the porous media;fjis the coefficient of linear thermal expansion of pore water.

Substituting Eq.(15) into Eq.(14), the motion equation in terms of displacement can be obtained as:

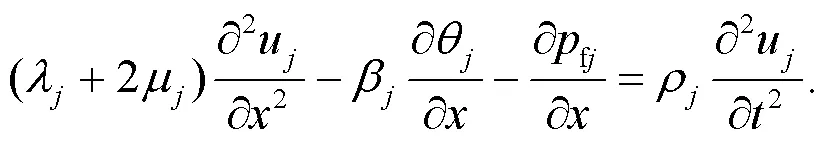
3 Solutions to governing equations

To solve Eqs.(12)–(17), the following dimensionless quantities are introduced:

x=12,t=122, τ=122τ,σ=σ/1,

θ=θ/0,q=q/(1012),fj=pfj/1,

where1=[(1+21)/1]1/2and2=1/1.In the dimensionless form, the governing Eqs.(12), (13), and (15)–(17) can be rewritten as:

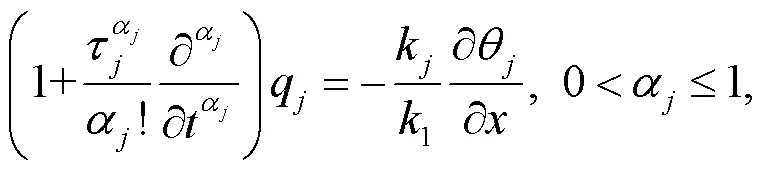
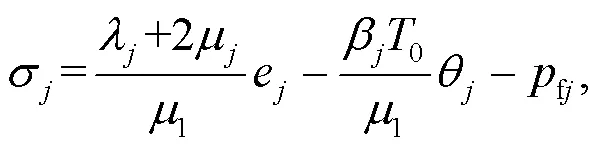
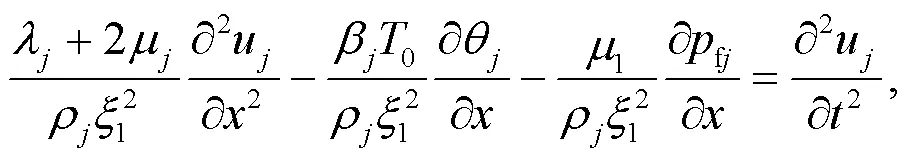
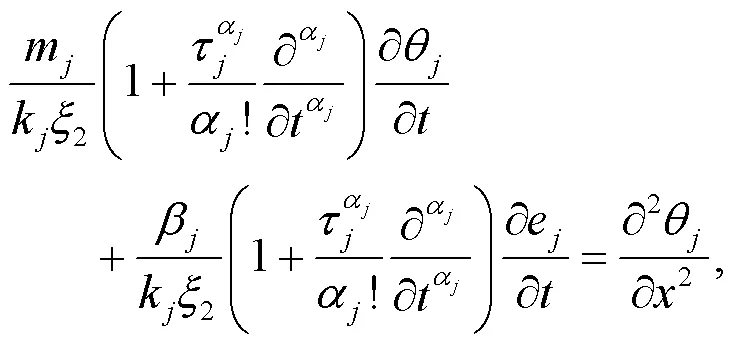
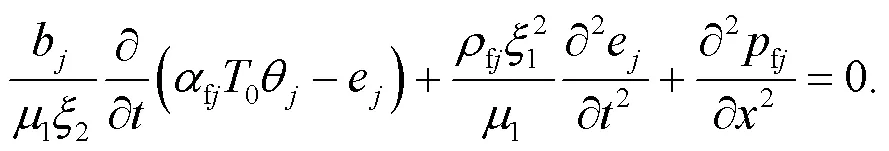
After multiplying ∂/∂on both sides, Eq.(20) can be rewritten as:

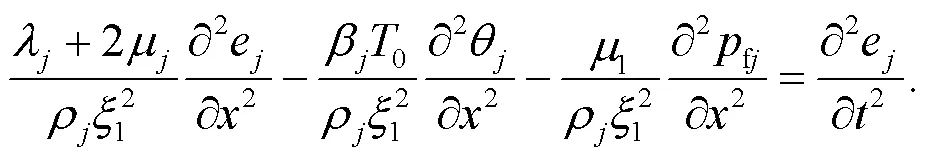
Combining Eqs.(22) and (23), the following expression can be derived:

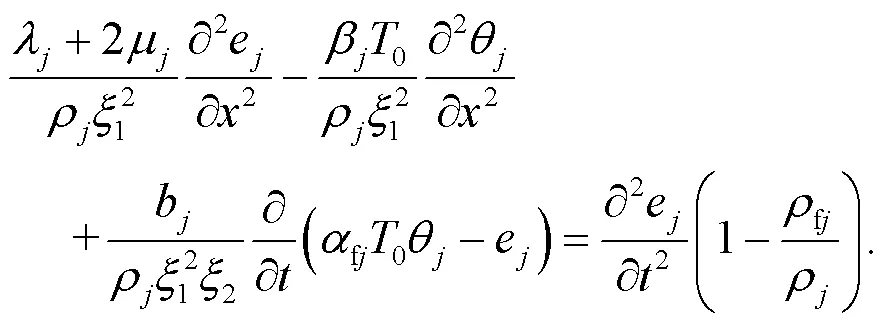
For steady-state vibration with an angular frequency of, Eqs.(24) and (21) can be respectively rewritten as:

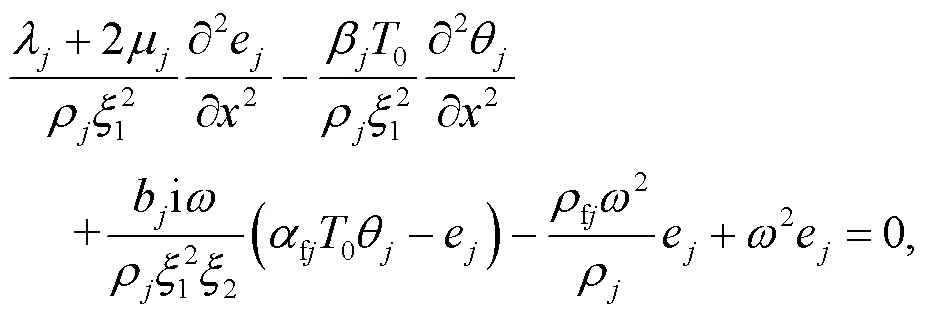
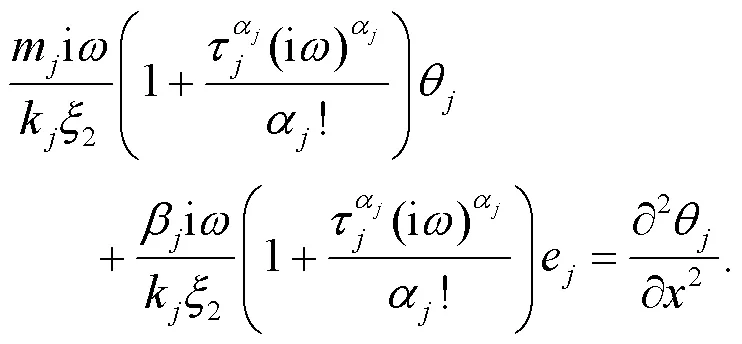
The analytic solutions of dynamic response of bilayered saturated porous media are obtained by Eqs.(19), (25), and (26), and the analytic expressions of temperature increment, displacement, pore water pressure, and stress are also obtained.So the problem may be completely solved.The solving process is neglected here and the reader is referred to electronic supplementary materials for detailed derivation.

4 Results and discussion

In this section, the effects of the fractional derivative parameters1and2, and the thermal contact resistanceTon the temperature increment, displacement, pore water pressure, and stress of a layered saturated porous media are systematically evaluated.Non-dimensional relaxation times of1=2=0.5 are adopted and the non-dimensional thickness of saturated porous medium 1 is set as=0.5.The non-dimensional frequency is set as=0.5, and the elastic wave impedance ratio is given as1/2=1.0.The material constants of saturated soil, which are assigned to saturated porous media 1 and 2, are shown in Table 1 (Lu et al., 2010; Wen et al., 2020).In addition,0=293 K and0=1.

4.1 Comparison and validation

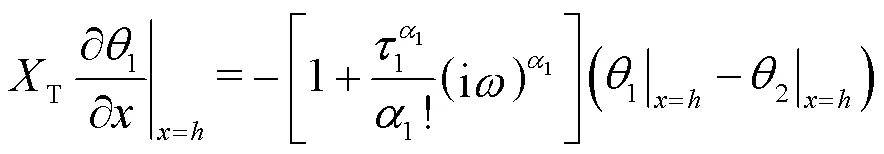
When1=2=0 andf1=0, the porous thermoelastic media in this study can be degraded into a thermoelastic solid.Therefore, replacing(denotes the complex variable in the Laplace domain) with iin the solution of Xue et al.(2016), the problem of Xue et al.(2016) can be degraded into the dynamic response problem of a bilayered thermoelastic media under harmonic thermal load.To validate the accuracy of the proposed solutions, the present results were compared with those reported by Xue et al.(2016).Fig.3 demonstrates the variations of temperature increment and displacement with the depth.The present results are generally consistent with those of Xue et al.(2016).WhenT=10−10, the interface (=0.5) is degraded into the continuity condition, i.e.=0.5.At this time, the thermal wave passes through the first layer and then completely reflects to the second layer of the thermoelastic media via the interface.At=0.5, the thermal gradient at the interface exhibits a jumping phenomenon, which becomes even more obvious with the increase ofT.

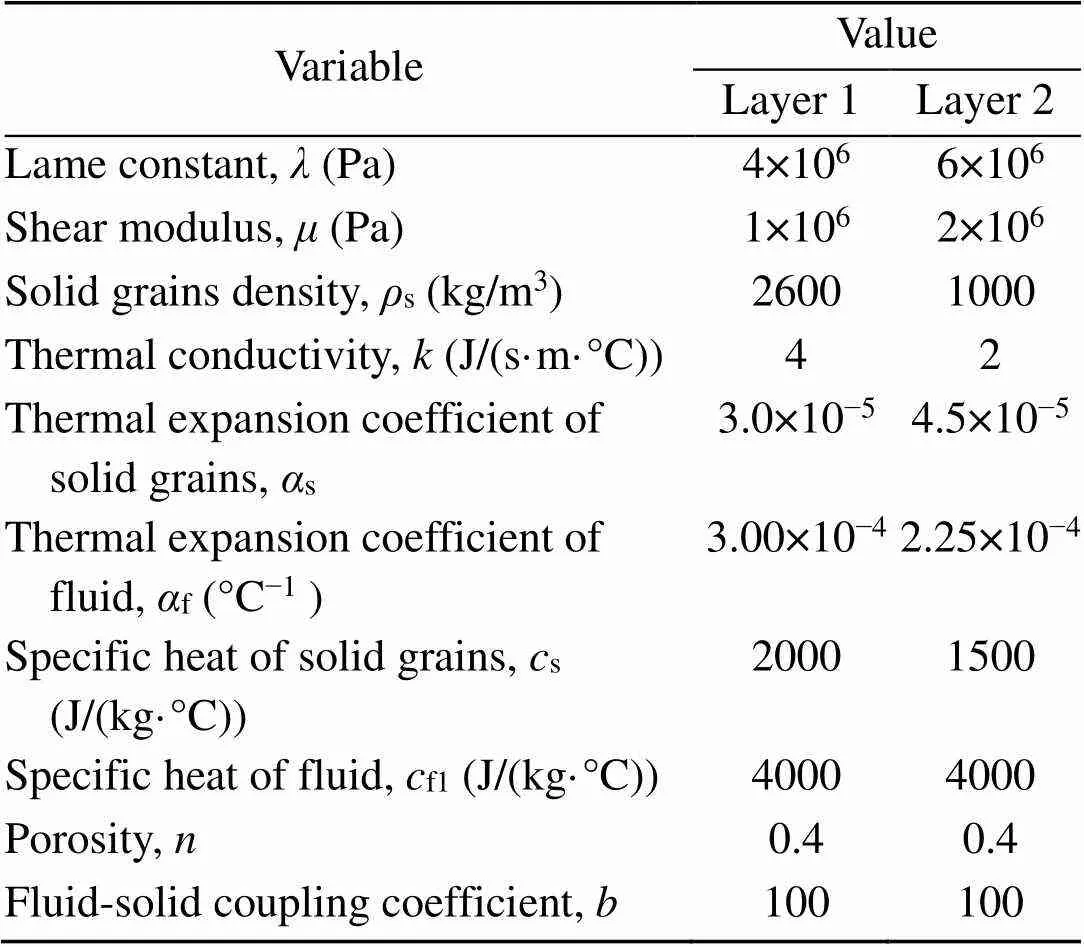
Table 1 Default parameters adopted in the parametric study (Lu et al., 2010; Wen et al., 2020)

4.2 Effects of fractional derivative parameters

Fig.4 shows the effects of the fractional derivative parameters1and2on the temperature increment, displacement, pore water pressure, and stress of the bilayered saturated porous media, whenT=10−10and1/2=1.0.When1=2=0.25, the heat conduction is weak, which results in relatively small magnitudes of temperature increment, displacement, pore water pressure, and stress.With the increase of1and2, the magnitude of the responses of these parameters increases significantly.On the other hand, when1=2=1.0, the heat conduction is strong.

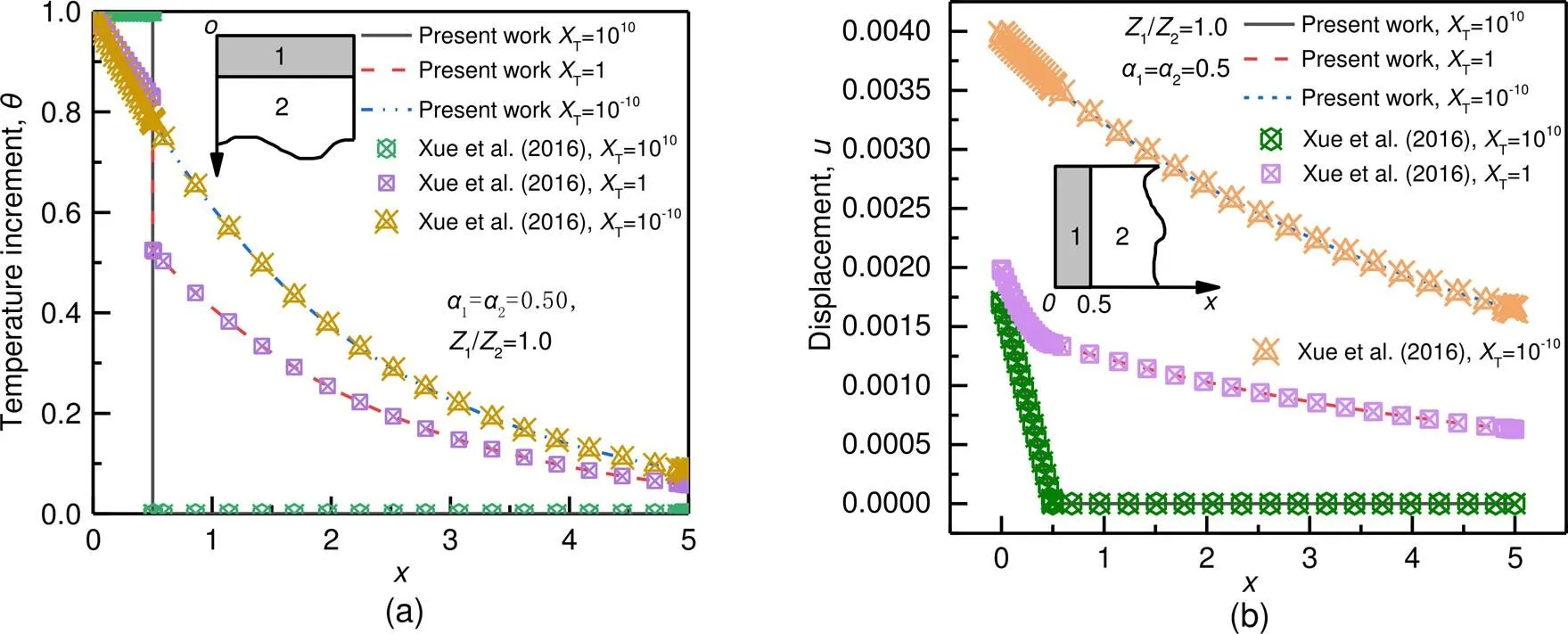
Fig.3 Comparison between the results of the present method and those reported by Xue et al.(2016)

(a) Temperature increment; (b) Displacement

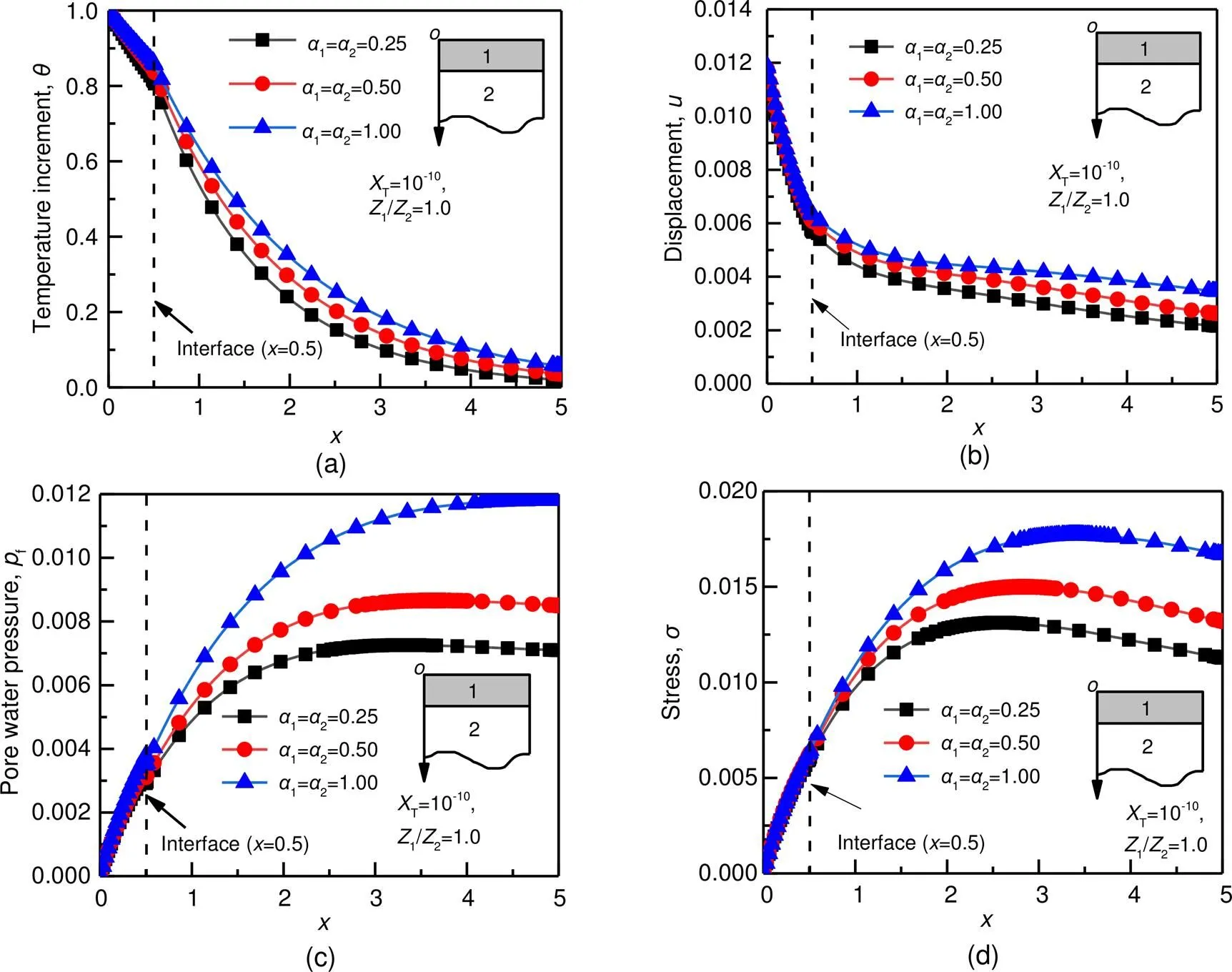
Fig.4 Effects of fractional derivative parameters on temperature increment (a), displacement (b), pore water pressure (c), and stress (d), when XT=10−10 and Z1/Z2=1.0

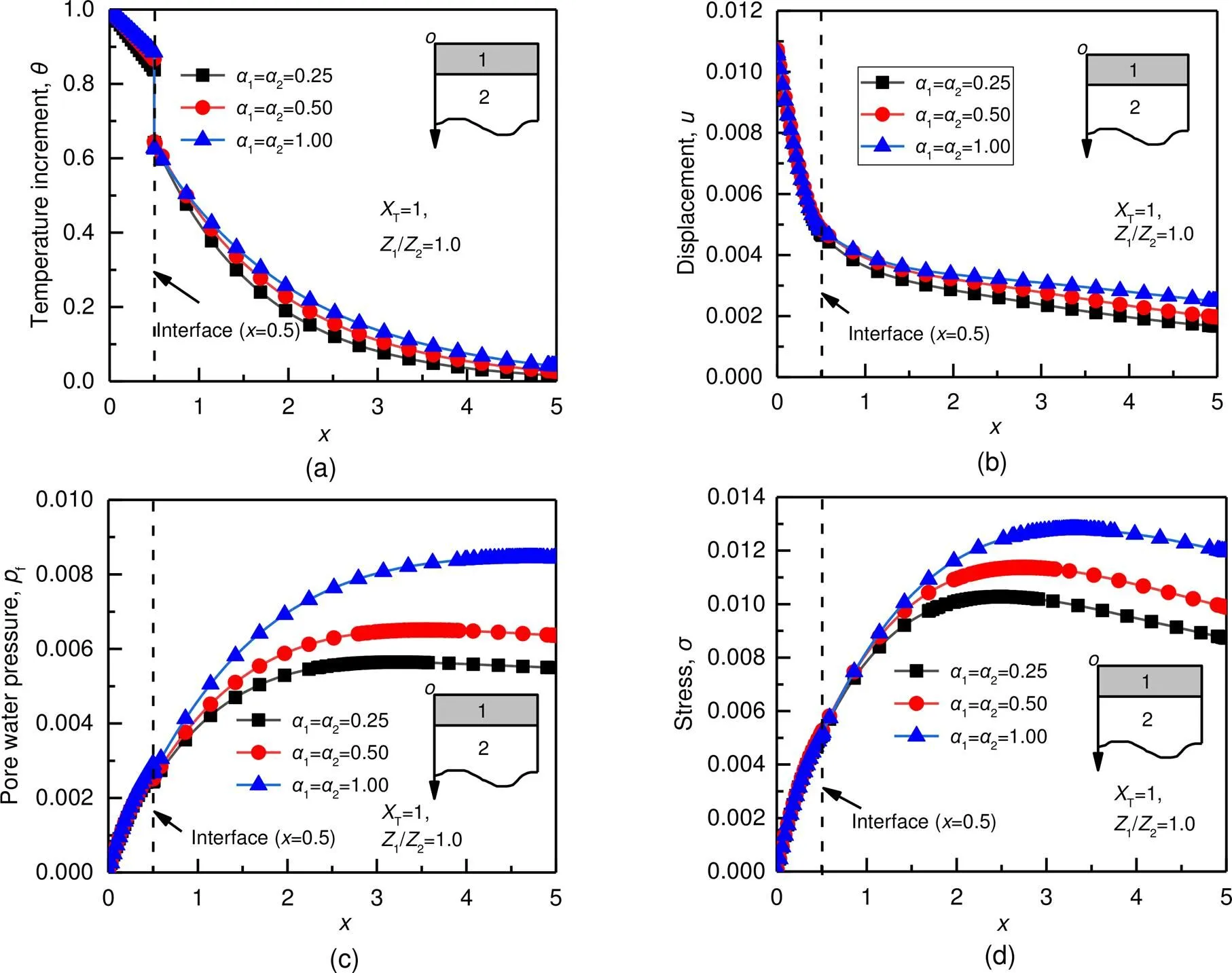
Fig.5 Effects of fractional derivative parameters on temperature increment (a), displacement (b), pore water pressure (c), and stress (d), when XT=1 and Z1/Z2=1.0

4.3 Effects of thermal contact resistance

Fig.8 (p.1001) shows the effect of thermal contact resistance on the temperature increment, displacement, pore water pressure, and stress of the bilayered saturated porous media, when1=2=0.5 and1/2=1.0.

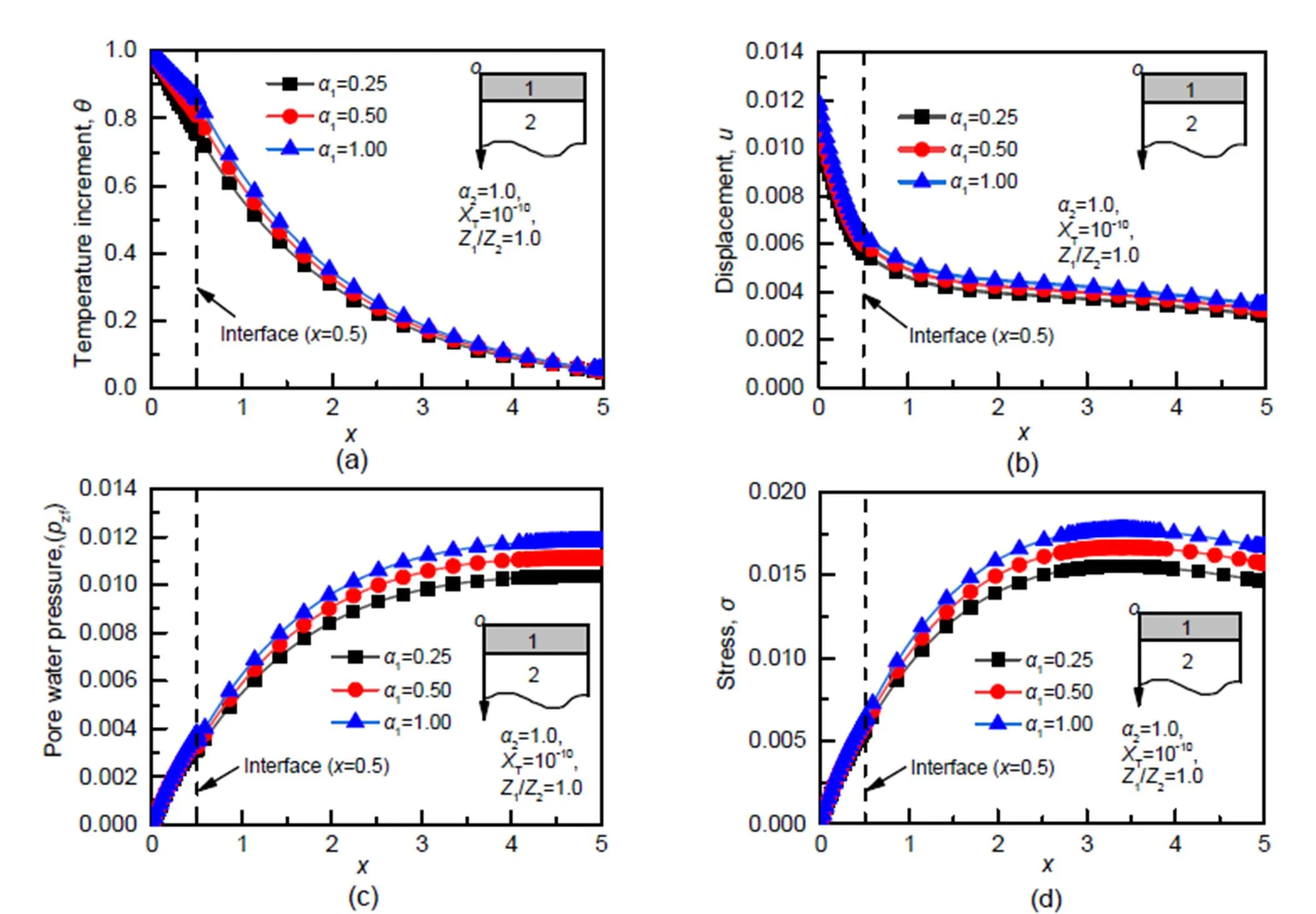
Fig.6 Effects of fractional derivative parameter α1 on temperature increment (a), displacement (b), pore water pressure (c), and stress (d), when XT=10−10 , Z1/Z2=1.0, and α2=1.0

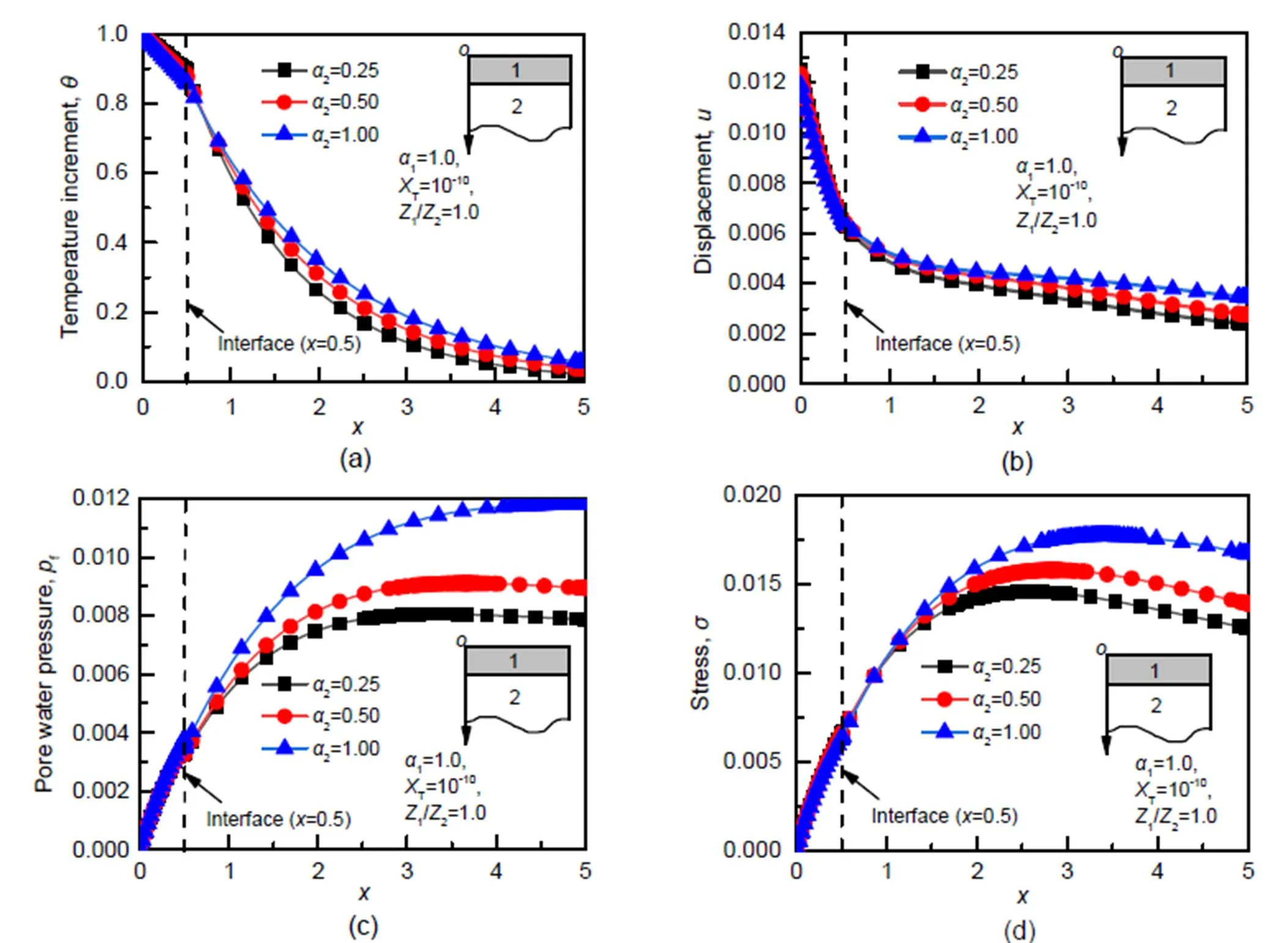
Fig.7 Effects of fractional derivative parameter α2 on temperature increment (a), displacement (b), pore water pressure (c), and stress (d), when XT=10−10 , Z1/Z2=1.0, and α1=1.0

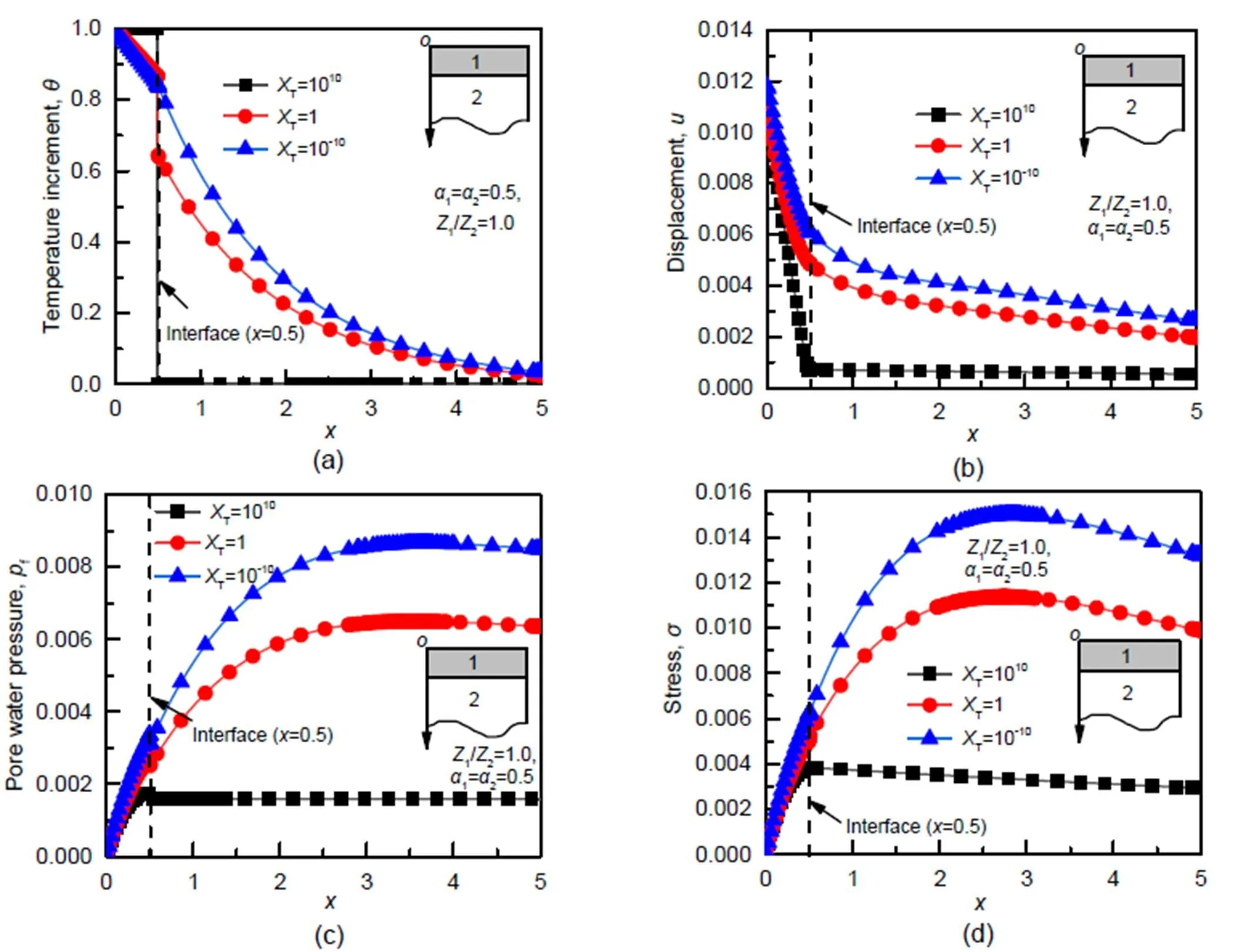
Fig.8 Effects of thermal contact resistance XT on temperature increment (a), displacement (b), pore water pressure (c), and stress (d), when α1=α2=0.5 and Z1/Z2=1.0

According to Fig.8a, forT=1010, the interface of the bilayered saturated porous media (=) is similar to that of a complete insulation condition, under which the heat wave can be completely reflected to the first layer when it passes through the interface.Therefore, the temperature increments in the first and second layers are close to 1 and 0, respectively.ForT=1, part of the heat wave enters the second layer through the interface, while another part is reflected, resulting in a sudden incremental leap in temperature at the interface.ForT=1010, the interface is close to the continuous boundary condition, and the heat wave can be fully transmitted to the second layer; thus, the temperature increment forms a smooth curve.In Fig.8b, forT=1010, the displacement of the second layer is almost equal to 0.This is because the temperature increment in the second layer is almost equal to 0, since most of the heat is reflected to the first layer.ForT=10−10, the contact surface satisfies the continuous boundary condition, and the heat can be completely transmitted to the second layer, producing great deformation between the two layers.As shown in Figs.8c and 8d, the pore water pressure and stress increase significantly with the decrease in the thermal contact resistance.When the contact surface approaches the insulation condition (T=10−10), the heat can be transmitted to the second layer after passing through the interface.Accordingly, the second layer exhibits a great temperature increase, accompanied by an increase in the pore water pressure and stress in the two layers.

5 Conclusions

In this paper, a fractional derivative THM coupling thermoelastic model of saturated porous media is developed based on fractional thermoelastic theory and the poroelastic wave equation.The thermal contact resistance and the elastic wave impedance at the interface are introduced to analyze the THM coupling dynamic response of a bilayered saturated porous media.After analyzing the effects of the fractional derivative parameters and thermal contact resistance on the dynamic response of the bilayered saturated porous media, the following conclusions could be drawn:

1.With the increase of the fractional derivative parameters1and2, the response amplitudes of the temperature increment, displacement, pore water pressure, and stress increase significantly.Moreover, the effect of fractional derivative parameters on the THM coupling response is related to the thermal contact resistance at the interface.If there is thermal contact resistance at the interface, the effect of the fractional derivative parameters on the system response is weakened.The fractional derivative parameters can reveal the heat conduction intensity and thermodynamic behavior of the THM coupling response of a bilayered saturated porous media.

2.The effect of the fractional derivative parameter2on the temperature increment, displacement, and pore water pressure of a bilayered saturated porous media is stronger than that of1.Furthermore, the response amplitudes of the second layer increase steadily as the fractional derivative parameter2increases.

3.Because of thermal contact resistance at the interface, the temperature increment at the interface exhibits a jumping phenomenon, which becomes more obvious as the thermal contact resistance increases.With the increase of thermal contact resistance, the displacement, pore water pressure, and stress at the interface decrease gradually.

List of electronic supplementary materials

Data S1 Derivation of the analytical solution for Eqs.(25) and (26)

Data S2 Derivation of the analytical solution for medium 2

Contributors

Min-jie WEN designed the research.Min-jie WEN and Kui-hua WANG processed the corresponding data.Min-jie WEN wrote the first draft of the manuscript.Wen-bing WU and Yun-peng ZHANG helped to organize the manuscript.Hou-ren XIONG revised and edited the final version.

Conflict of interest

Min-jie WEN, Kui-hua WANG, Wen-bing WU, Yun-peng ZHANG, and Hou-ren XIONG declare that they have no conflict of interest.

Abbas IA, Marin M, 2018.Analytical solutions of a two-dimensional generalized thermoelastic diffusions problem due to laser pulse., 42(1):57-71.https://doi.org/10.1007/s40997-017-0077-1

Abbas IA, Alzahrani FS, Elaiw A, 2019.A DPL model of photothermal interaction in a semiconductor material.,29(2):328-343.https://doi.org/10.1080/17455030.2018.1433901

Ai ZY, Wang LJ, 2015a.Axisymmetric thermal consolidation of multilayered porous thermoelastic media due to a heat source.,39(17):1912-1931.https://doi.org/10.1002/nag.2381

Ai ZY, Wang LJ, 2015b.Time-dependent analysis of 3D thermo-mechanical behavior of a layered half-space with anisotropic thermal diffusivity.,226(9): 2939-2954.https://doi.org/10.1007/s00707-015-1360-0

Ai ZY, Wang LJ, 2016.Three-dimensional thermo-hydro-mechanical responses of stratified saturated porothermoelastic material.,40(21-22):8912-8933.https://doi.org/10.1016/j.apm.2016.05.034

Ai ZY, Ye Z, Zhao Z, et al., 2018.Time-dependent behavior of axisymmetric thermal consolidation for multilayered transversely isotropic poroelastic material.,61:216-236.https://doi.org/10.1016/j.apm.2018.04.012

Alzahrani F, Abbas IA, 2020.Generalized thermoelastic interactions in a poroelastic material without energy dissipations.,41(7): 95.https://doi.org/10.1007/s10765-020-02673-0

Alzahrani F, Hobiny A, Abbas I, et al., 2020.An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities.,12(5):848.https://doi.org/10.3390/sym12050848

Bhatti MM, Marin M, Zeeshan A, et al., 2020.Swimming of motile gyrotactic microorganisms and nanoparticles in blood flow through anisotropically tapered arteries.,8:95.https://doi.org/10.3389/fphy.2020.00095

Biot MA, 1956.Thermoelasticity and irreversible thermodynamics.,27(3):240-253.https://doi.org/10.1063/1.1722351

Booker JR, Savvidou C, 1984.Consolidation around a spherical heat source.,20(11-12):1079-1090.https://doi.org/10.1016/0020-7683(84)90091-X

Carr EJ, March NG, 2018.Semi-analytical solution of multilayer diffusion problems with time-varying boundary conditions and general interface conditions.,333:286-303.

https://doi.org/10.1016/j.amc.2018.03.095

Deswal S, Kalkal KK, 2013.Fractional order heat conduction law in micropolar thermo-viscoelasticity with two temperatures.,66:451-460.https://doi.org/10.1016/j.ijheatmasstransfer.2013.07.047

Ezzat MA, El-Karamany AS, El-Bary AA, 2015.On thermo-viscoelasticity with variable thermal conductivity and fractional-order heat transfer.,36(7):1684-1697.https://doi.org/10.1007/s10765-015-1873-8

Green AE, Lindsay KA, 1972.Thermoelasticity.,2(1):1-7.https://doi.org/10.1007/BF00045689

He TH, Zhang P, Xu C, et al., 2019.Transient response analysis of a spherical shell embedded in an infinite thermoelastic medium based on a memory-dependent generalized thermoelasticity.,42(8):943-961.https://doi.org/10.1080/01495739.2019.1610342

Hobiny A, Abbas I, 2020.Fractional order GN model on photo-thermal interaction in a semiconductor plane.,12(8):1957-1964.https://doi.org/10.1007/s12633-019-00292-5

Hobiny A, Abbas I, 2021.Analytical solutions of fractional bioheat model in a spherical tissue.,49(3):430-439.https://doi.org/10.1080/15397734.2019.1702055

Hussein EM, 2015.Fractional order thermoelastic problem for an infinitely long solid circular cylinder.,38(2):133-145.https://doi.org/10.1080/01495739.2014.936253

Hussein EM, 2018.Effect of the porosity on a porous plate saturated with a liquid and subjected to a sudden change in temperature.,229(6):2431-2444.https://doi.org/10.1007/s00707-017-2106-y

Kek-Kiong T, Sadhal SS, 1992.Thermal constriction resistance: effects of boundary conditions and contact geometries.,35(6):1533-1544.https://doi.org/10.1016/0017-9310(92)90043-R

Khan AA, Bukhari SR, Marin M, et al., 2019.Effects of chemical reaction on third-grade MHD fluid flow under the influence of heat and mass transfer with variable reactive index.,50(11):1061-1080.https://doi.org/10.1615/HeatTransRes.2018028397

Levy A, Sorek S, Ben-Dor G, et al., 1995.Evolution of the balance equations in saturated thermoelastic porous media following abrupt simultaneous changes in pressure and temperature.,21(3):241-268.https://doi.org/10.1007/BF00617408

Li CL, Tian XG, He TH, 2020.Transient thermomechanical responses of multilayered viscoelastic composite structure with non-idealized interfacial conditions in the context of generalized thermoviscoelasticity theory with time-fractional order strain.,43(7):895-928.https://doi.org/10.1080/01495739.2020.1751760

Li CX, Xie KH, 2013.One-dimensional nonlinear consolidation of soft clay with the non-Darcian flow., 14(6):435-446.https://doi.org/10.1631/jzus.A1200343

Li CX, Xie KH, Wang K, 2010.Analysis of 1D consolidation with non-Darcian flow described by exponent and threshold gradient., 11(9): 656-667.https://doi.org/10.1631/jzus.A0900787

Li CX, Xie KH, Hu AF, et al., 2012.One-dimensional consolidation of double-layered soil with non-Darcian flow described by exponent and threshold gradient., 19(2):562-571.https://doi.org/10.1007/s11771-012-1040-3

Li CX, Wang CJ, Lu MM, et al., 2017.One-dimensional large-strain consolidation of soft clay with non-Darcian flow and nonlinear compression and permeability of soil., 24(4):967-976.https://doi.org/10.1007/s11771-017-3499-4

Li CX, Xiao JY, Wu WB, et al., 2020.Analysis of 1D large strain consolidation of structured marine soft clays., 21(1):29-43.https://doi.org/10.1631/jzus.A1900268

Liu GB, Xie KH, Zheng RY, 2009.Model of nonlinear coupled thermo-hydro-elastodynamics response for a saturated poroelastic medium.,52(8):2373-2383.https://doi.org/10.1007/s11431-008-0220-8

Liu GB, Liu XH, Ye RH, 2010a.The relaxation effects of a saturated porous media using the generalized thermoviscoelasticity theory.,48(9):795-808.https://doi.org/10.1016/j.ijengsci.2010.04.006

Liu GB, Xie KH, Zheng RY, 2010b.Thermo-elastodynamic response of a spherical cavity in saturated poroelastic medium.,34(8):2203-2222.https://doi.org/10.1016/j.apm.2009.10.031

Lord HW, Shulman Y, 1967.A generalized dynamical theory of thermoelasticity.,15(5):299-309.https://doi.org/10.1016/0022-5096(67)90024-5

Lu Z, Yao HL, Liu GB, 2010.Thermomechanical response of a poroelastic half-space soil medium subjected to time harmonic loads.,37(3):343-350.https://doi.org/10.1016/j.compgeo.2009.11.007

Mei GX, Yin JH, 2008.Coupled model of consolidation and creep for consolidation test., 15(S1):357-361.https://doi.org/10.1007/s11771-008-0380-5

Mei GX, Chen QM, 2013.Solution of Terzaghi one-dimensional consolidation equation with general boundary conditions., 20(8):2239-2244.https://doi.org/10.1007/s11771-013-1730-5

Peng W, Ma YB, Li CL, et al., 2020.Dynamic analysis to the fractional order thermoelastic diffusion problem of an infinite body with a spherical cavity and variable material properties.,43(1):38-54.https://doi.org/10.1080/01495739.2019.1676681

Saeed T, Abbas I, Marin M, 2020.A GL model on thermo-elastic interaction in a poroelastic material using finite element method.,12(3):488.https://doi.org/10.3390/sym12030488

Sherief HH, Hussein EM, 2012.A mathematical model for short-time filtration in poroelastic media with thermal relaxation and two temperatures., 91(1):199-223.https://doi.org/10.1007/s11242-011-9840-8

Sherief HH, El-Latief AMA, 2013.Effect of variable thermal conductivity on a half-space under the fractional order theory of thermoelasticity.,74:185-189.https://doi.org/10.1016/j.ijmecsci.2013.05.016

Sherief HH, El-Sayed AMA, El-Latief AMA, 2010.Fractional order theory of thermoelasticity.,47(2):269-275.https://doi.org/10.1016/j.ijsolstr.2009.09.034

Sherief HH, El-Latief AMA, 2015.A one-dimensional fractional order thermoelastic problem for a spherical cavity.,20(5):512-521.https://doi.org/10.1177/1081286513505585

Singh B, 2013.Elastic wave propagation and attenuation in a generalized thermoporoelastic model.,9(2):256-267.https://doi.org/10.1108/MMMS-04-2013-0032

Tao HB, Liu GB, Xie KH, et al., 2014.Characteristics of wave propagation in the saturated thermoelastic porous medium.,103(1):47-68.https://doi.org/10.1007/s11242-014-0287-6

Wang LJ, Wang LH, 2020.Semianalytical analysis of creep and thermal consolidation behaviors in layered saturated clays.,20(4): 06020001.https://doi.org/10.1061/(asce)gm.1943-5622.0001615

Wang N, Wang KH, Wu WB, 2013.Analytical model of vertical vibrations in piles for different tip boundary conditions: parametric study and applications., 14(2):79-93.https://doi.org/10.1631/jzus.A1200184

Wen MJ, Xu JM, Xiong HR, 2020.Thermo-hydro-mechanical dynamic response of a cylindrical lined tunnel in a poroelastic medium with fractional thermoelastic theory.,130:105960.https://doi.org/10.1016/j.soildyn.2019.105960

Xue ZN, Yu YJ, Li CL, et al., 2016.Application of fractional order theory of thermoelasticity to a bilayered structure with interfacial conditions.,39(9):1017-1034.https://doi.org/10.1080/01495739.2016.1192451

Xue ZN, Yu YJ, Tian XG, 2017.Transient responses of multi-layered structures with interfacial conditions in the generalized thermoelastic diffusion theory.,131-132:63-74.https://doi.org/10.1016/j.ijmecsci.2017.05.054

Xue ZN, Yu YJ, Li XY, et al., 2019.Study of a generalized thermoelastic diffusion bi-layered structures with variable thermal conductivity and mass diffusivity.,29(1):34-53.https://doi.org/10.1080/17455030.2017.1397810

Xue ZN, Tian XG, Liu JL, 2020.Non-classical hygrothermal fracture behavior of a hollow cylinder with a circumferential crack.,224: 106805.https://doi.org/10.1016/j.engfracmech.2019.106805

Youssef HM, 2007.Theory of generalized porothermoelasticity.,44(2):222-227.https://doi.org/10.1016/j.ijrmms.2006.07.001

Youssef HM, 2010.Theory of fractional order generalized thermoelasticity.,132(6): 061301.https://doi.org/10.1115/1.4000705

Yovanovich MM, 2005.Four decades of research on thermal contact, gap, and joint resistance in microelectronics.,28(2):182-206.https://doi.org/10.1109/TCAPT.2005.848483

Yuan KL, Wen MJ, Wang WY, et al., 2021.Nonlocal thermodynamic response of thermal insulation layer-substrate wall system considering the temperature-dependent thermal material properties.,44(2):214-235.https://doi.org/10.1080/01495739.2020.1837043

Zhang YP, Liu H, Wu WB, et al., 2021.A 3D analytical model for distributed low strain test and parallel seismic test of pipe piles.,225:108828.https://doi.org/10.1016/j.oceaneng.2021.108828

Zhang YP, Jiang GS, Wu WB, et al., 2022.Analytical solution for distributed torsional low strain integrity test for pipe pile., 46(1):47-67.https://doi.org/10.1002/nag.3290

Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering)

ISSN 1673-565X (Print); ISSN 1862-1775 (Online)

www.jzus.zju.edu.cn; link.springer.com

E-mail: jzus_a@zju.edu.cn

# Electronic supplementary materials: The online version of this article (https://doi.org/10.1631/jzus.A2100084) contains supplementary materials, which are available to authorized users

© Zhejiang University Press 2021

Feb.20, 2021;

Revision accepted June 25, 2021;

CrosscheckedNov.22, 2021

https://doi.org/10.1631/jzus.A2100084

TU473.4

*Project supported by the National Natural Science Foundation of China (Nos.52108347 and 51779217), the Primary Research and Development Plan of Zhejiang Province (Nos.2019C03120 and 2020C01147), China