电网储能系统优化配置策略分析

杨一敏

(国网浙江省电力有限公司江山市供电公司，浙江江山，324100)

0 引言

配电网在实际运行过程中，通常需要接入分布式电源，实现多主体供电，在这一过程中，很容易导致各节点电压出现超限问题，影响整体电网运行稳定性。基于此，有必要加强对配电网储能系统优化配置分析，这对维护电网运行稳定有着非常重要的意义。

1 电网储能电池改善电网电压的原理分析

在我国，配电网类型以辐射式电网位置，在没有接入DGs（是指由多个计算机组成一个电力控制系统）的情况下，系统在运行时，潮流方向由首端开始，然后流向末端。反之， 配电网既要为负荷供电，自身也成为一种多电源供电系统，这必然会改变电网潮流方向与大小。当DGs向电网注入功率时，在对应节点处，电压会有所提升，从而影响电网电压质量。而对接有分布式电源的配电网系统来说，为促使节点电压质量得到有效改善，文章引入了电池储能系统，在节点电压出现越限现象时，引导储能系统参与功率调度过程，从而能够有效调整电网电压，维护电网整体电压稳定性。在有分布式电源接入配电网的情况下，如果忽略线路损耗，那么线路节点电压可用以下公式表示：

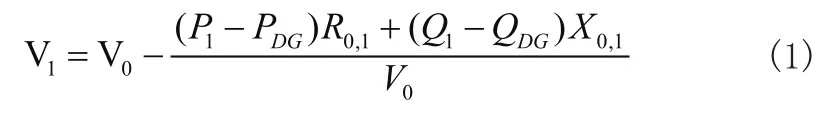
在（1）中，V0表示节点0处电压，V1表示节点1处电压；P1表示节点1处的有功功率；Q1表示节点1处的无功功率；PDG表示节点1在接入分布式电源后，系统的有功功率；QDG表示节点1在接入分布式电源后，系统的无功功率[1]。从中我们能够了解到，在配电网中增加分布式电源的有功注入量，P1-PDG值会逐渐变小，一旦有功注入量足够多，P1-PDG值会变成负数，从而致使V1＞V0，在这一情况下，对支路1末节点电压值而言，将会比首端节点电压值要大，由此可证明，随着分布式电源在配电网之中接入，在该节点处，电压可能会处于升高状态。

文章通过接入储能系统，用于电压越限问题改善，具体可采用以下表达式：

在（2）式中，PESS代表的是调度储能系统的充电功率。若该公式合理，那么P1+PESS-PDG会成为正值。此时，在支路1两端，相较于末端，首端电压会更大。而在节点1处的电压越限问题便能够得到妥善解决。

2 电网储能系统优化模型构建策略

2.1 科学合理进行储能选址

通过上文我们能够了解到，科学利用储能系统，能有效确保各节点之间的电压稳定性，保障电网安全运行。因此，文章采用节点电压与实际电压之差的平方来作为地址分配的依据，来保障储能选址的科学合理性。具体表达式如下：

在（3）式中，Vj表示的是某节点实际电压值，VN表示的是网络额定电压值。在某节点之中，如果电压出现了较大偏移量，可选择这一节点，作为储能装置的接入位置，从而在该装置的帮助下，实现对该节点电压的控制。

2.2 储能装置容量配置策略

在实际进行储能容量配置时，应在满足节点电压的条件下，尽可能地加强配电网经济运行成本的控制。在储能系统之中，建设成本的大小，一般与能量和功率有着非常密切的关系。因此在实际进行模型建立时，应以储能系统在接入配电网后，实际构建经济最小化作为目标函数，具体函数可由以下公式表示：

在（4）式中，f1与f2分别代表配电网的运行成本与配电网储能建设成本。前者具体是指，在电网与外界交互的过程中，所产生的电能成本，具体可用以下函数公式表示：

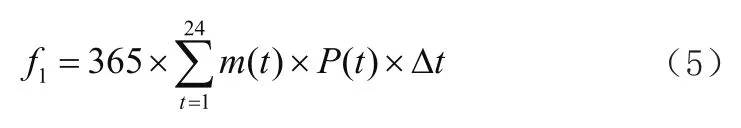
在上述（5）式中，m(t)代表的是在t时刻下，配电网与外界交互功率实际电价。P(t)则代表的是配电网与上级网络交互的功率。

后者是指储能实际的建设成本，具体可用以下函数公式表示：

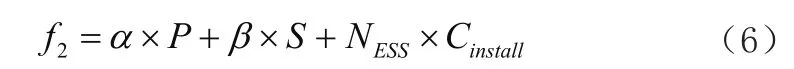
在上述（6）式中，α与β分别代表单位功率成本（单位：元/kW）与单位容量成本（单位：元/kWh）；Cinstall代表的是储能安装建设单位成本；P与S则分别代表的是储能额定功率与储能配置容量，NESS则表示，在配电网之中，实际接入储能电源的数量。

2.3 约束条件

(1)潮流平衡约束。在实际开展优化结果的计算时，应满足配电网有功与无功平衡约束，具体由以下公式表示：

在上述（7）式中，Pi代表的是注入节点i的有功功率；Qi代表的是注入节点i的无功功率；e代表的还是节点电压实部分量；f代表的还是节点电压虚部分量；Gij代表的是节点导纳矩阵的实分量；Bij代表的是节点导纳矩阵的虚分量；n代表的是节点总数量。

(2)节点电压约束。先通过实施潮流计算，获得在馈线内部，相应电压指标，从而能够确保在各个节点之中，电压变化均在规定范围内。约束条件用以下公式表示：

(3)储能功率约束。该约束的存在，主要是保证在储能系统进行充放电时，始终在合理范围内，不超出上限或者下限。具体约束条件可用以下公式表示：

在上述（9）式中，-Pmax与 ≤Pmax分别表示储能系统充放电的下限与上限。

(4)支路电流约束。该约束条件的存在，主要是确保各支路电流始终在标准限值内。具体可用以下公式表示：

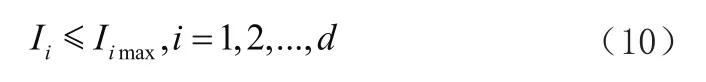
在上述（10）式中，Iimax代表的是第i条支路电流上限，d代表的是系统内支路总数。

3 算例仿真分析

为对上述策略准确性及可行性进行验证，文章选择IEEE 11节点的配电系统，如图1所示。在该系统中，将基准电压设定为12.65 kV，实际功率值设置为10MVA。在节点4、8、11处，接入了0.45MW与3MW的光伏电源与4MW风电[2]。储能系统功率成本为1650元/kW，单位容量成本为1270元/kWh, 假设基础建设成本为10万元/次。在配电网与外界交互中，在0至6点与22至24点，实时电价为0.3元/kW·h。在6至8点与11至17点时段，实时电价为0.5元/kW·h。在8至11点与17至22点时段，实时电价为0.8元/kW·h。

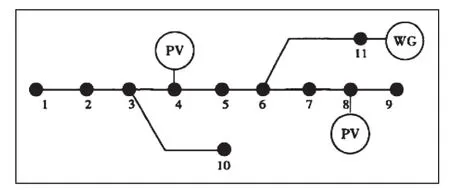
图1 包含DGs的配电网算例示意图

在储能选址结果方面，由于在本次研究中，采用潮流计算，获得了各节点时序电压值，本次选择第 12时段实施分析。从最终结果来看，在节点1位置，节点电压与基准值的差值平方最小，究其原因在于，该位置与母线位置比较接近，因此在该节点处，如果注入功率，几乎不影响节点电压，因此无需在此位置进行储能系统的安装。而通过结果可知，在7、8、9节点位置处，电压偏移量最大[3]。为保证配电网运行稳定，并确保选择的储能位置不相邻，

因此应选择在中间节点8处，接入储能系统。而在节点10位置处，则是除了上述7、8、9节点之外电压偏差最大的位置，同样满足储能系统接入位置不相邻条件，因此也可以选择在该位置处接入储能系统。

在对储能容量配置结果分析时，应结合实际情况，选择一条供电线路典型日负荷， 包括商业负荷和居民负荷等。在本次研究中，选择某地典型日的负荷曲线，该曲线包括风电出力和光伏出力，具体如图2所示。

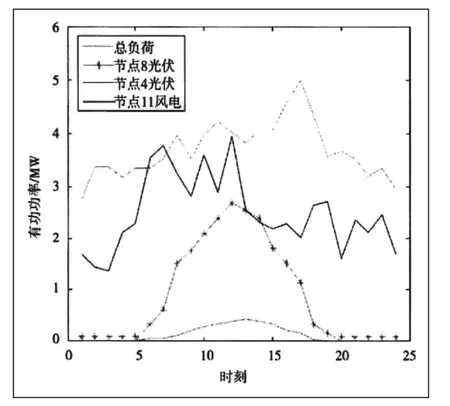
图2 负荷曲线与DG出力曲线

由于在本次研究中，馈线支路较少，并且在实际配置储能系统时，需要投入的成本也比较高，因此在配电网系统中，不宜接入过多储能系统。具体的储能接入方案可包括两种，第一种接入方案，直接入一个储能系统，接入位置在节点8，储能系统的额定功率为1200kW，储能容量为2780kWh，需要消耗成本为629.7万元。而第二种接入方案则接入两个储能系统，第一个储能系统接到节点8位置，该系统额定功率为400kW，储能容量为1517kWh；第二个储能系统接入到节点10位置，该系统额定功率为580kW，储能容量为1040kWh。总投入成本为554.5万元。

通过对比两种方案我们可以发现，相较于第一种方案，第二种方案显然更优，且消耗的成本也最低。究其原因在于，单独在节点8接入一个储能系统，需要提供非常高的功率，才能保证节点10的电压处于规定电压范围之内。单个高功率储能系统成本更高。通过在节点8与节点10接入两个小功率储能系统，同样能解决电压偏移问题，而且实际消耗成本更低。因此方案二属于最佳方案。从实践来看，通过采用方案二对配电网储能进行优化配置后，结合如图3所示的各节点电压时序变化曲线图，我们能够了解到电压越限情况没有再出现，整个时段均处于0.95至1.05pu之间，有效实现了问题解决。

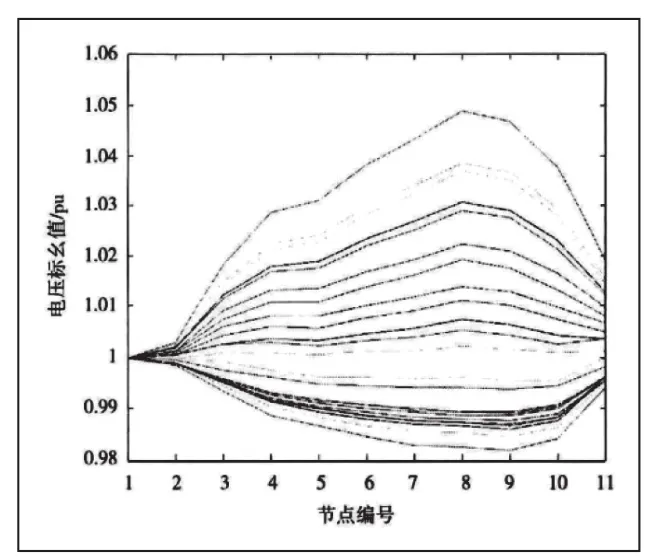
图3 接入储能系统后全时段电压标幺值

4 总结

配电网储能系统的接入，对于整体电网电压稳定有着直接的影响。因此需要我们充分考虑实际，加强对配电网储能系统的优化，促使系统中各个节点电压的越限情况得到解决，确保系统中各节点电压幅值 都在规定范围内，更好地维护配电网安全稳定运行。