双基地探测下空间同步问题分析

陈春杰，干昌浩

（江南机电设计研究所，贵州贵阳，550009）

0 引言

随着信息科学技术的发展，双（多）基地雷达以较强的生存能力、较高的探测功能及较好的“四抗”能力又重新引起了人们的关注。双（多）基地雷达由于其系统构成和几何配置的原因带来了时间同步、空间同步和相位同步问题。本文将重点分析空间同步的影响因素，对各影响因素进行建模和仿真，并给出减小空间同步误差的方法。

1 双基地雷达空间同步影响因素

双基地雷达除发射站和接收站不在一个位置外，其探测目标的原理与单基地雷达基本一致。发射站根据接收站测量的目标坐标信息、发射站和接收站的站址位置，将目标坐标信息转换为以发射站为中心的目标坐标信息，控制发射站照射波束指向，并发射信号照射目标。接收站根据自身测量的目标坐标信息实时控制接收波束指向，完成对目标照射回波信号的接收，从而实现对目标的检测、跟踪。

在双基地目标探测时，若照射波束指向与目标真实位置存在较大偏差，势必将影响双基地雷达的探测能力。影响双基地雷达空间同步的主要因素如下：（1）目标测量误差：发射站将接收站测量的目标坐标信息经坐标转换后，用于控制照射波束指向；因此，接收站的目标测量误差势必将影响照射波束指向的准确性。（2）目标信息传输延迟：发射站与接收站异地布置，目标坐标信息从接收站传输至发射站，势必会带来发射站接收目标坐标信息的延迟，从而带来照射波束指向的滞后。（3）站址定位误差：在照射波束指向控制数据计算中，需要将接收站测量的目标坐标信息，转换至以发射站为原点的目标坐标信息；因此，双站（接收站和发射站）站址定位的准确性将对照射波束指向产生影响。（4）寻北误差：目标测量误差中含寻北误差，而发射站的寻北误差直接影响照射波束指向的准确性。

综上分析，上述因素将导致照射波束不能准确的指向目标位置，进而影响双基地雷达对目标的探测。

2 双基地雷达空间同步建模和仿真

2.1 空间同步建模

在双基地目标探测中，发射站、接收站和目标几何关系如图1所示。

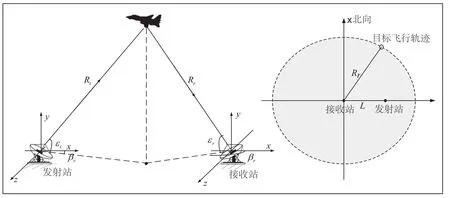
图1 双基地目标探测发射站、接收站和目标几何关系图

在图1中：Rr、rε、rβ分别为以接收站为原点的目标斜距、高低角和方位角，即接收站根据发射站照射目标回波信号测量出的目标坐标信息；Rt、εt、βt为以发射站为原点的目标斜距、高低角和方位角。

（1）存在测量误差的目标坐标信息

接收站测量的目标坐标信息为目标信息真值和目标测量误差之和，即：

公式中：Rr0、εr0和βr0分别为目标的真实斜距、高低角和方位角；

Δrm、Δεm和Δβm分别为接收站的目标测量斜距误差、高低角误差和方位角误差。

（2）目标坐标信息的传输延迟补偿

发射站与接收站异地布置，为了解算目标相对发射站的坐标，接收站测量目标坐标信息需从接收站传输至发射站，因而发射站接收的目标信息会产生传输延时。该传输延迟带来的误差需通过目标坐标信息及双站传输延时进行补偿，补偿公式如下：

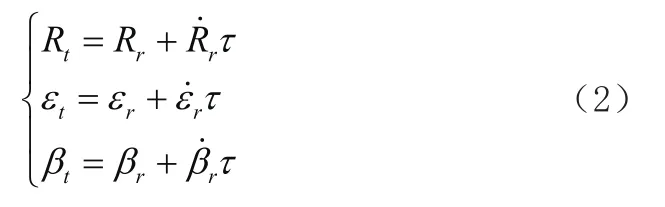
公式中，τ为双站传输延时。

（3）存在站址定位误差的站址位置

假设接收站的经度、纬度和海拔高度真值分别为：Jr0、Wr0、Hr0，测量的接收站经度、纬度和海拔高度为：

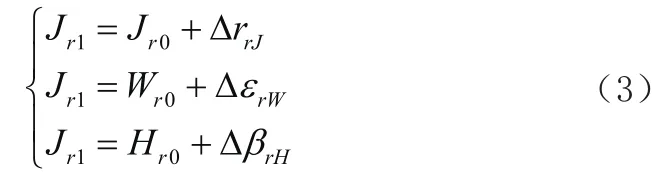
公式中：

Jr1、Wr1和Hr1分别为发射站的经度、纬度和海拔高度；

ΔrrJ、ΔεrW和ΔβrH分别为发射站的经度、纬度和海拔高度测量误差。

同理可得到测量的发射站经度、纬度和海拔高度为Jt1、Wt1和Ht1。

（4）大地直角坐标系下发射站相对接收站的位置

大地直角坐标系下，发射站相对接收站的位置计算公式为：

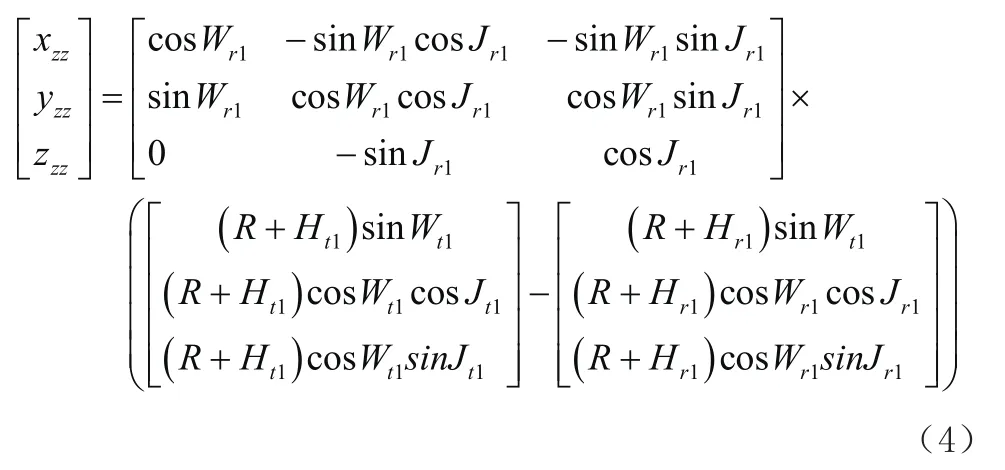
公式中，为地球半径：R=6371226m。

（5）大地直角坐标系下接收站测量的目标坐标信息

将接收站测量的目标信息从大地极坐标系转换到大地直角坐标系见公式(5)：

（6）大地直角坐标系下目标相对发射站的位置

大地直角坐标系下，接收站测量的目标坐标转换到以发射站为原点的目标坐标见公式(6)：

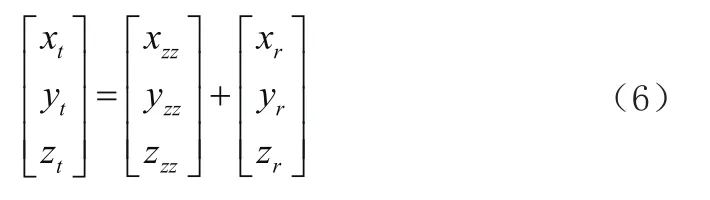
（7）大地极坐标系下目标相对发射站的位置

将以发射点为中心的目标坐标信息从大地直角坐标系转换到大地极坐标系见公式(7)～公式(9)：

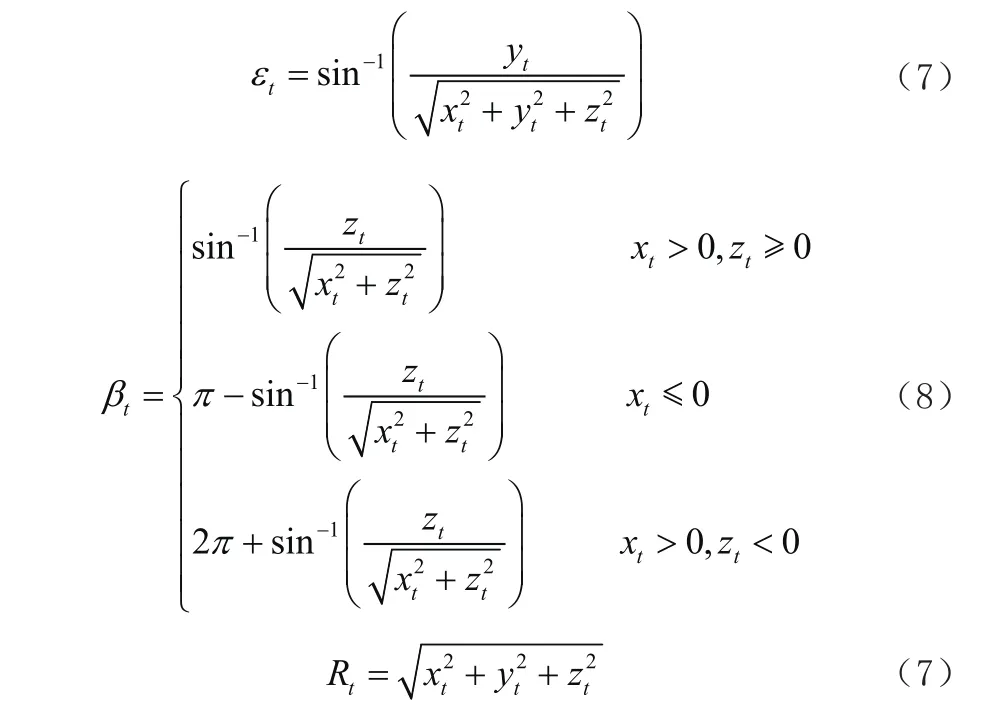
2.2 空间同步误差的仿真分析

目标坐标信息的传输延迟可通双站时延进行补偿，因此在仿真中未考虑传输延项的影响。对站址定位误差、目标测量误差、寻北误差等对照射波束指向的影响进行分析，具体如下。

（1）站址定位误差的影响

假设发射站与接收站之间的基线距离L分别为500m、1000m、1500m和2000m，发射站与接收站连线与正北方向垂直（夹角为90°，如图1所示），站址相对距离定位误差10m，目标相对于接收站的斜距100km、高度5km时，对目标围绕接收站做圆周运动情况下的站址定位误差对照射波束指向的影响进行仿真；照射波束指向随目标方位角的变化如图2所示。

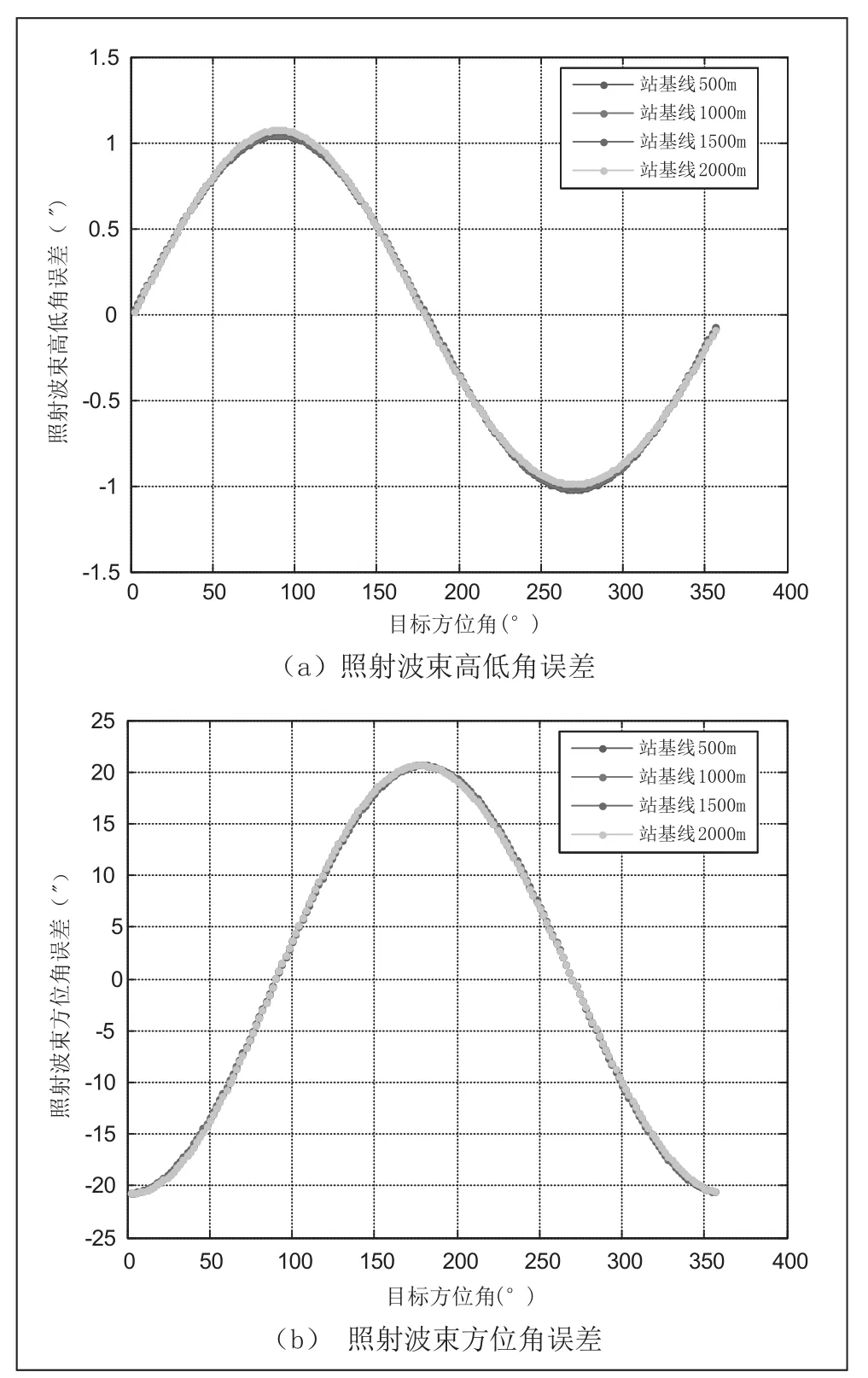
图2 站址定位引起的照射波束指向误差与目标方位角的关系

从图2中可以看出，随着目标方位角在0°～360°变化，站址定位误差引起的照射波束指向误差成震荡性变化。

（2）目标测量误差的影响

假设目标角度测量误差0.3°、距离测量误差50m、站址相对距离定位误差0m，其它条件同（1）条进行仿真，照射波束指向随目标方位角的变化如图3所示。

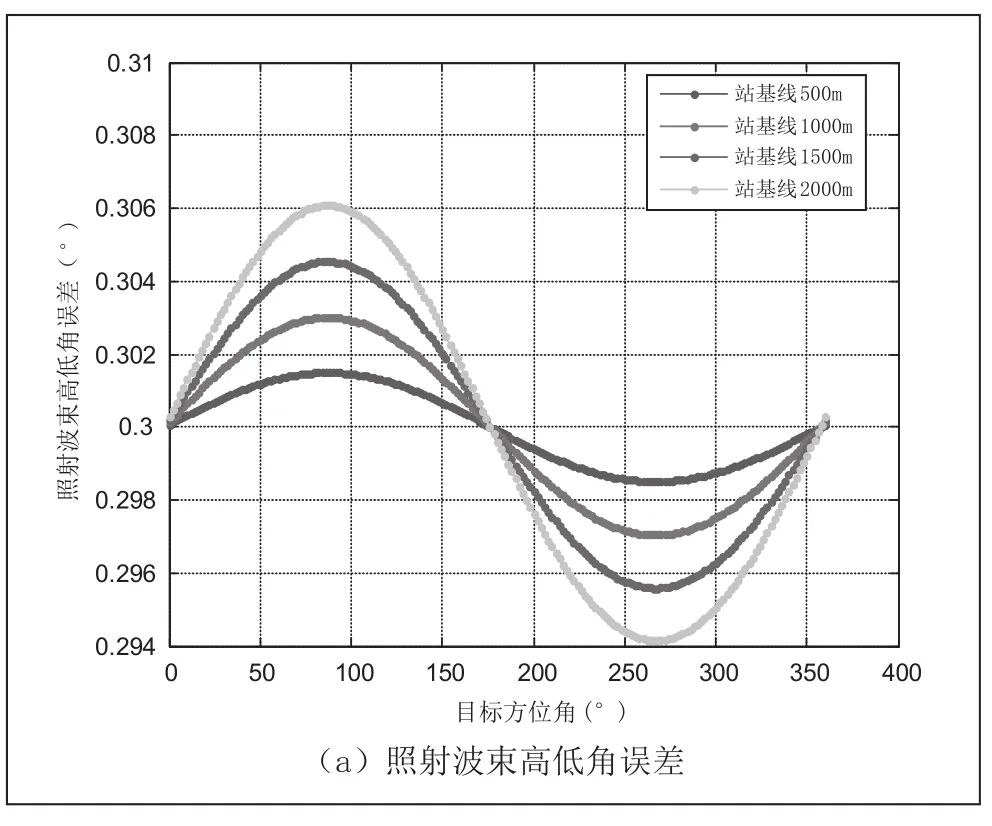
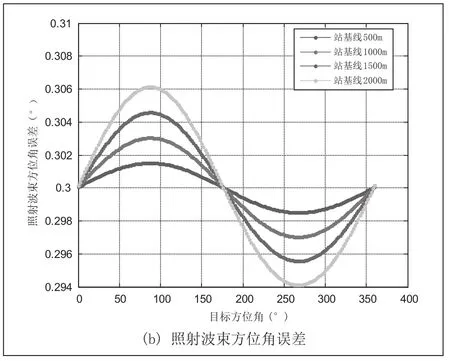
图3 目标测量引起的照射波束指向目标随方位角的关系

从图3中可以看出，随着目标方位角在0°～360°变化，目标测量误差引起的照射波束指向误差在目标角度测量误差（0.3°）上下做周期变化，且误差最大值随着站址基线长度的增大而增大。

（3）寻北误差的影响

假设发射站的寻北误差为0.05°、站址相对距离定位误差0m，其它条件同（1）条进行仿真，照射波束指向随目标方位角的变化如图4所示。

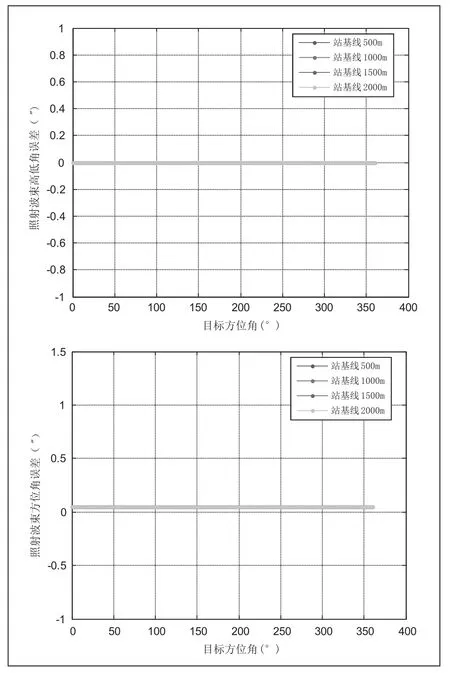
图4 寻北引起的照射波束指向目标随方位角的关系

从图4中可以看出，在不同站址基线下照射波束指向误差一样，寻北误差直接引入到照射波束方位指向中，对照射波束高低指向不产生影响。

2.3 减小空间同步误差的方法

基于空间同步误差的仿真分析结果，减小空间同步误差的方法如下：（1）站址误差：随着目标方位角在0°～360°的变化，站址误差引起的照射波束指向误差成震荡性变化。因此，在使用中通过合理布置发射站与接收站的位置来减小其对照射波束指向的影响。（2）目标测量误差：目标测量误差中有系统量和起伏量，因此可通过对系统误差进行补偿以减小其对照射波束的影响。（3）寻北误差：寻北误差直接引入到照射波束方位指向中，因此在照射波束方位指向中对寻北误差进行补偿。

综上所述，寻北误差为系统量，目标测量误差中也有部分系统量，因此可通过对系统误差进行补偿以减小其对照射波束指向的影响。站址测量误差、目标测量误差与目标相对接收站的方位角成震荡性变化，可根据主攻方向合理布置发射站和接收站，减小其对照射波束指向的影响。

3 结束语

影响双基地探测下空间同步的因素有站址定位误差、目标测量误差、寻北误差、目标与双站之间位置等。双基地雷达空间同步仿真结果表明：采用高精度寻北，合理布置发射站、接收站的位置，可减小其对照射波束指向的影响；同时采用对照射波束系统误差补偿的方法，可减小目标测量误差、寻北误差对照射波束指向的影响。