一种适用于少子模块MMC全电平模式混合调制策略

许仪勋， 冯紫妍， 张建浩， 汪凯琳， 王桂莲

(1.上海电力大学 电气工程学院，上海 200090; 2. 广东电网有限责任公司，广东 梅州 514000; 3.华北电力大学 新能源电力系统国家重点实验室， 河北 保定 071003；4. 运能电力科技有限公司,山西 运城 044099)

0 引 言

随着分布式电源渗透率的增加与电力电子技术的进步发展，直流配电网凭借其显著优势受到了广泛关注[1，2]。相较于交流配电网，直流配电网供电容量大、传输效率高且线路损耗小，无需考虑三相不平衡及无功补偿等问题[3，4]。模块化多电平换流器(modular multilevel converter，MMC)具有结构模块化、控制灵活、易于拓展等优势，广泛应用于高压直流输电领域，其控制方式、故障保护方案等已有大量研究[5-7]。MMC通过模块化设计可有效抬高输出电压并改善电压质量，交流侧无需传统两电平或三电平换流器中的复杂滤波环节，平均开关频率和运行损耗较低[8-10]。对于直流配电网中的DC/AC或DC/DC电能变换环节，MMC及其衍生拓扑已成为研究热点。

由于直流配电网电压等级的限制，MMC子模块数量较少，调制方式是确保MMC安全稳定及经济运行的关键环节，根据不同的应用场合需求，一般有传统最近电平逼近调制(nearest level modulation，NLM)和载波移相PWM调制(carrier phase-shifted pulse width modulation，CPS-PWM)两种方式。NLM策略通过电平数累加使阶梯波逼近调制波，但直流配电网中少子模块MMC的输出电压存在较多的低次谐波[11，12]；CPS-PWM输出电压波形质量较高，但运行损耗较高，依赖复杂的均压控制和环流抑制算法[13，14]。因此，亟需对适合少子模块MMC的调制策略展开研究，以改善直流配电网中MMC的运行性能。

在NLM、CPS-PWM等传统策略的基础上，已有多种新型MMC调制策略被相继提出。文献[15]改进NLM调制策略使得输出电平数量倍增，有效的改善电压波形质量，但增大了循环电流，限制了其向工程应用方面推广。文献[16]详细介绍了载波重叠脉冲宽度调制(Phase Disposition pulse width modulation PD-PWM)，但是该调制方式依赖于复杂控制策略实现子模块电压均衡，因此对控制系统提出了较高的要求。文献[17-18]主要介绍了特定谐波消除脉冲宽度调制(Selective harmonic elimination pulse width modulation，SHE-PWM)在子模块数较少的直流配电网中可稍微减小谐波含量，但触发角计算方法较为复杂。文献[19]深入研究了载波重叠PWM(phase disposition PWM，PD-PWM)调制策略，利用算法实现子模块电压的均衡，但对控制系统要求较高。文献[20]提出了一种最近电平PWM(nearest level PWM，NL-PWM)混合调制策略，在NLM阶梯波的基础上叠加了PWM波，可改善少子模块MMC的波形质量并避免了复杂的电压均衡控制，但循环电流畸变率较高。文献[21]提出了一种包含基频调制(fundamental frequency modulation，FFM)和多载波PWM的混合调制策略，以减小MMC的运行损耗，但存在子模块电压越限问题，需配合复杂的电压均衡控制。

上述新型调制方式在提高交流侧电压质量的同时带来了诸如循环电流较大、控制复杂、运行损耗高等弊端，在少子模块MMC中尤为明显，较CPS-PWM并无明显优势。为提高MMC在直流配电网中的适用性，本文提出一种适用于少子模块MMC全电平(Full level)模式下的NL-PWM混合调制策略(以下简称“FL-NL-PWM”)。在子模块数量较少的直流配电网中，该策略可根据电压质量要求对交流侧等效电平数进行多级倍增，降低输出电压中难以滤除的低次谐波含量。

本文首先给出典型三相MMC的全电平模式，并介绍传统NLM与CPS-PWM的调制策略及其弊端。其次，提出FL-NL-PWM调制策略，并设计与之适应的电压排序方法。再次，对FL-NL-PWM进行循环电流与谐波特性分析，并确定其最优方波频率。最后，基于MATLAB/Simulink仿真平台搭建MMC仿真模型，对所提调制策略的有效性与优越性进行验证。

1 全电平模式及传统调制策略

1.1 全电平模式

根据输出电压电平数目，典型三相MMC的调制方式包含为两种模式，分别为基本电平模式和全电平模式。基本电平模式下，输出电压含有N+1个电平，全电平模式则含有2N+1个电平，其中N为桥臂子模块数，如图1所示。电平数越多，输出电压与正弦参考波的拟合程度越高，谐波畸变率越低。

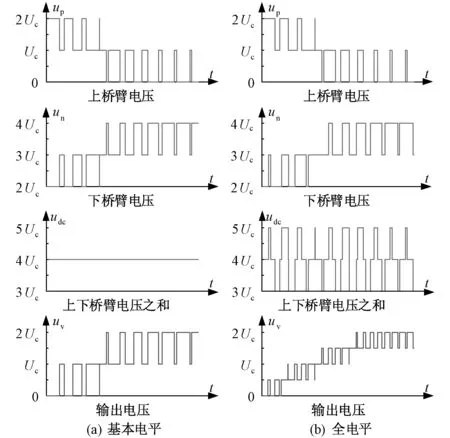
图1 调制模式Fig. 1 Modulation modes

基本电平模式下，每一相单元上、下桥臂投入的子模块数目Npj、Nnj(j=a，b，c)满足

Npj+Nnj=N

(1)

此时，上、下桥臂输出电压之和为Udc，输出电压的电平数目为N+1，谐波畸变率较高。当交流电压的输出电平变化时，Npj和Nnj都会相应的变化，相单元中子模块的投入和切除同时发生。

在全电平模式下，上、下桥臂所投入子模块数不再呈互补关系，Npj与Nnj之和可以是N-1、N或者N+1，输出电压的电平数目为2N+1，谐波畸变率较低。当交流电压的输出电平变化时，Npj和Nnj不会同时变化，相单元中子模块的投入或切除不会同时发生。相比于基本电平模式，全电平模式下的输出电压的电平数和电平跳变次数近似倍增，可有效改善输出电压的波形质量。

1.2 传统调制策略

为了方便阐述NL-PWM调制策略工作在全电平模式下的特性，这里对广泛采用的NLM和CPS-PWM两种传统调制策略进行简要概述。

1.2.1 NLM调制策略

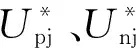
(2)

上、下桥臂输出电压Upj、Unj

(3)

式中：round为四舍五入取整函数；Δ为参考电压偏移量，通过调整Δ可以改变电平阶跃变化的时刻。当NLM处于基本电平模式，Δ取值为0；当NLM处于全电平模式时，Δ可表示为

(4)

式中：sgn(x)为符号函数，取值为x>0，sgn(x)=1，x=0，sgn(x)=0。

相比于基本电平模式，全电平模式下少子模块MMC输出电压的电平数量更多，输出电压阶梯波与正弦参考波的拟合程度更高、谐波畸变率更低，如图2所示。全电平模式下，NLM调制策略的上、下桥臂电压之和中电平跳动的频率较低，扰乱了循环电流的波形。

考虑到电网中的高次谐波可被限流电抗器有效滤除，本文重点关注MMC输出电压的总谐波畸变率THD和小于2000Hz的低次谐波畸变率THDL。根据文献[22]给出的NLM谐波特性分析，可得采用NLM时MMC输出交流电压的THD和THDL随桥臂子模块数N的变化情况，如图3所示。可见，采用NLM时少子模块MMC的输出电压中THDL占主要成分；全电平模式下，NLM调制的输出电压的THD和THDL明显低于基本电平模式；THD和THDL均随着N的增加而降低。

图3 NLM调制下输出电压的谐波畸变率Fig. 3 THD of output voltage under NLM

NLM利用排序算法维持子模块电容电压均衡，仅在电平跳变时刻重新排序以确定子模块工作状态，因此少子模块MMC中电容电压的排序次数较少，均衡程度较低。当扩展到全电平模式时，桥臂电流中的低频循环电流含量增加，导致子模块电容电压的不均衡程度进一步增加。

1.2.2 CPS-PWM调制策略

理想情况下，各子模块的正弦参考波相同、三角载波相位互差2π/N，桥臂中N个子模块独立调制，桥臂输出N+1电平PWM波。当上、下桥臂对应子模块的载波相位相同时，CPS-PWM处于基本电平模式；当载波相位相差π/N时，CPS-PWM处于全电平模式，如图4所示。全电平模式下，上、下桥臂电压之和中电平跳动的频率较高，对于循环电流影响较小。

图4 不同调制模式下CPS-PWM的输出电压Fig. 4 Output voltage of CPS-PWM under different Modulation modes

考虑到不同调制策略的载波个数存在差异，本文定义了平均载波频率fc_ave，CPS-PWM调制的fc_ave与载波频率fc相等。根据文献[23]对CPS-PWM的谐波特性分析，可得少子模块MMC输出电压的THD和THDL随fc_ave的变化情况，如图5所示。参照图3可知，CPS-PWM输出电压的THD高于NLM，THDL低于NLM。由图5可知，CPS-PWM输出电压的THD随着fc_ave的增加变化不大，但THDL显著降低；THD和THDL都随着N的增加而降低；全电平模式下，输出电压的THD和THDL都小于基本电平模式。

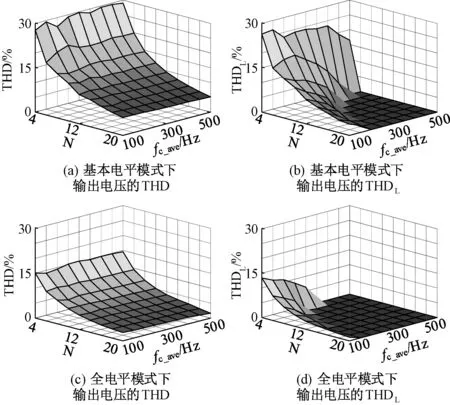
图5 不同调制模式下CPS-PWM输出电压的THD及THDLFig. 5 THD and THDL of output voltage of CPS-PWM under different modulation modes

为了降低少子模块MMC输出电压的THDL，需要维持fc_ave处于较高水平，从而增加MMC运行损耗。此外，CPS-PWM的桥臂参考信号需要叠加均压控制信号和环流抑制信号，控制复杂且增大了调制结果与理想参考信号之间的偏差。

2 NL-PWM的全电平调制模式

由上文可知，全电平模式下两种传统调制策略NLM和CPS-PWM应用于少子模块MMC时均存在相应的弊端。本文研究了FL-NL-PWM调制策略，以满足实际工程对于电能质量与经济性的要求。

2.1 调制原理

与CPS-PWM调制方式不同，NL-PWM每个桥臂仅需要一个三角载波即可调制出多电平PWM波，如图6所示。NL-PWM对桥臂电压参考波向下取整得到阶梯波，如图6(a)所示。然而，阶梯波与参考波之间存如图6(b)所示偏差，可将该偏差作为PWM参考波，得到如图6(c)所示的PWM波对阶梯波进行补充。将PWM波与阶梯波相叠加，即可近似输出N+1电平PWM波，如图6(d)所示。与CPS-PWM调制相比，NL-PWM调制方法简单，且不需要考虑子模块数目。

图6 NL-PWM调制原理Fig. 6 Schematic diagram of NL-PWM

根据上述分析可知，上、下桥臂处于阶梯波状态的子模块个数Npj_s和Nnj_s可表示为

(5)

式中：floor为向下取整函数。

(6)

NL-PWM调制下，交流电压的电平数目和三角载波的相位紧密相关，当相单元中上、下桥臂的三角载波相位相差180°时，NL-PWM处于基本电平模式；当相单元中上、下桥臂的三角载波相位相同时，NL-PWM处于全电平模式，如图7所示。全电平模式下，上、下桥臂电压之和中电平跳动的频率较高，对于循环电流影响较小。

图7 不同调制模式下NL-PWM的输出电压Fig. 7 Output voltage of NL-PWM under different Modulation modes

NL-PWM调制下，上、下桥臂PWM脉冲序列为Npj_p和Nnj_p，则上、下桥臂所投入的子模块总数可表示为

(7)

NL-PWM调制下，各桥臂中只有一个载波，因此fc_ave=fc/N。基本电平调制模式下，NL-PWM调制的上、下桥臂投入子模块数目之和为N；全电平模式下，上、下桥臂投入子模块数目之和不再为N，而在N-1、N与N+1之间跳变。

2.2 子模块排序方式

传统NLM调制策略下，需要根据电容电压排序的结果确定各子模块的工作状态，以保证子模块电容电压均衡。若沿用与NLM相同的排序方法，NL-PWM的开关频率将会大大增加，导致MMC的运行损耗较高。如果采用传统排序思想，即桥臂阶梯波电平数变化时重新排序以确定子模块的工作状态，然而子模块排序和PWM脉冲都会引起电平跳动，增加MMC的运行损耗。

(8)

当采用修正后的电容电压进行排序时，不需要考虑桥臂电流的方向，而且每次开关动作只会涉及1个子模块，每个桥臂中所有子模块的开关频率之和为Nfc_ave。每次开关动作时，优先投入处于切除状态的子模块中修正电容电压最高的子模块，优先切除处于投入状态的子模块中修正电容电压最低的子模块，以保证电容电压均衡。全电平模式下，少子模块MMC采用修正后子模块电容电压的排序方法如图8所示。

图8 子模块排序方式流程图Fig. 8 Process of submodules sorting method

3 调制方式特性分析

3.1 循环电流分析

分析图7(b)可知FL-NL-PWM上、下桥臂投入子模块数目之和在N-1、N和N+1之间跳动，因此环流中存在高频成分；由于子模块电容电压存在波动，环流中也相应会存在倍频成分。循环电流icir的表达式为

icir=I2sin(2ωt+θ2)+Iksin(kωt+θk)

(9)

式中：I2和Ik分别为低次和高次环流的幅值;θ2和θk分别为低次和高次环流的相角。高次谐波的阶数为

k=2N·fc_ave

(10)

由于高次谐波的阶数较高，采用桥臂电抗器就可以很好的抑制，而低次谐波则很难被抑制，本文采用如图9所示环流抑制策略抑制二倍频负序环流。

图9 环流抑制策略Fig. 9 Circulate current suppressing strategy

为了对比基本电平模式和全电平模式下NL-PWM调制策略的循环电流，本文利用Matlab/Simulink搭建了如图10所示的仿真模型，仿真参数如表1所示。两种调制模式下，循环电流波形如图11所示。

表1 模型参数Tab.1 Model parameters

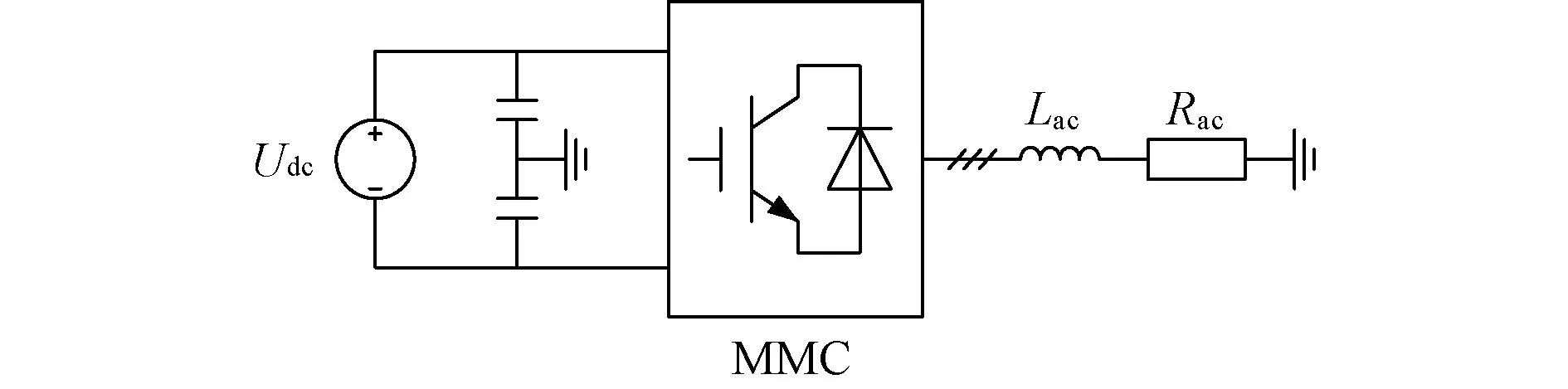
图10 MMC仿真模型Fig. 10 Simulation model of MMC

分析图11可知，基本电平模式下，循环电流较为稳定，倍频环流和高频环流成分均不明显。全电平模式下，倍频环流成分被环流抑制器消除，高次环流成分略微高于基本电平调制，但环流的波动整体在可控的范围之内，并不会对交流系统产生较大影响。

图11 NL-PWM调制的循环电流Fig. 11 Circulate current of NL-PWM

3.2 谐波分析

根据文献[20]中对NL-PWM的谐波特性分析，可得采用NL-PWM时输出电压的THD和THDL随平均载波频率fc_ave的变化情况，如图12所示。参照图3可知，NL-PWM下输出电压的THD高于NLM，THDL低于NLM。由图12可知，NL-PWM输出电压的THD随着fc_ave的增加变化不大，但THDL显著降低；THD和THDL都随着N的增加而降低；全电平模式下，输出电压的THD和THDL都小于基本电平模式。

图12 NL-PWM调制下输出电压的THD及THDLFig. 12 THD and THDL of output voltage under NL-PWM

等效载波频率为250 Hz时，FL-NL-PWM的谐波频谱计算值如图13所示。由图13可知，电压谐波主要为高次谐波，其中低次谐波含量较低，对交流系统的影响较小。因此，FL-NL-PWM的波形质量较好。

图13 FL-NL-PWM调制的谐波频谱计算值Fig. 13 Calculated harmonic spectrum of FL-NL-PWM

实际仿真中，电容电压的实时值与额定值之间存在偏差，此外，需要在桥臂电压参考值上叠加环流抑制信号，导致实际输出电压与理想值之间存在偏差。为了验证全电平模式下，谐波畸变率随平均载波频率fc_ave的变化情况，本文用Matlab/Simulink搭建了如图10和表1所示的仿真模型，结果如图14所示。

图14 全电平模式下三种调制策略的谐波畸变率对比Fig. 14 THD of three modulation strategies under full level mode

NLM调制下，桥臂子模块开关频率之和需要根据排序结果确定。NL-PWM和CPS-PWM调制下，桥臂子模块的开关频率之和均为Nfc_ave，因此运行损耗也大小相当。由图14可知，全电平模式下，NL-PWM和CPS-PWM的低次谐波畸变率随着平均载波频率fc_ave的增加而减小；当平均载波频率fc_ave较大时，NL-PWM的THDL小于NLM和CPS-PWM；NL-PWM的THD则大于NLM，小于CPS-PWM。

4 仿真验证

为了验证FL-NL-PWM应用于少子模块MMC的有效性与优越性，本文利用Matlab/Simulink搭建了如图10和表1所示的仿真模型。根据图14可知，当平均载波频率fc_ave大于250 Hz时，CPS-PWM和NL-PWM的谐波畸变率变化不大，因此仿真中fc_ave设定为250 Hz。此时CPS-PWM调制的载波频率为250 Hz，NL-PWM调制的载波频率为1 500 Hz。

图15给出了全电平模式下，NLM、CPS-PWM以及NL-PWM三种调制策略的仿真结果。对比电压波形与频谱可知，NLM调制下子模块处于低频开关变化状态，输出电压的高次谐波畸变率较低；但是，由于子模块数较少导致输出电压电平数较少，电压的THDL较高；当CPS-PWM调制处于全电平模式时，每个桥臂的6个子模块均工作在PWM状态，输出电压的高次谐波畸变率较高、低次谐波畸变率较低，且子模块的高频开关变化导致MMC的运行损耗较高；当NL-PWM调制处于全电平模式时，每个桥臂中所有的子模块轮换触发高频PWM信号，保证电容电压均衡的同时避免子模块处于高频开关跳动状态。此外，NL-PWM中所有子模块均处于低频开关跳动状态，输出电压的THDL小于NLM与CPS-PWM，THD也介于NLM与CPS-PWM之间。感性负载可滤除电流中的高次谐波，对比电流波形及其频谱可知，NLM的输出电压中THDL较高而导致电流发生明显畸变，电流的谐波畸变率最高；CPS-PWM的输出电压中THDL大于NL-PWM，因此NL-PWM输出电流的谐波畸变率小于CPS-PWM。对比子模块电容电压可知，NLM和NL-PWM均根据电容电压排序结果确定子模块的工作状态并，子模块电容电压变化趋势也较为相似，但NL-PWM的电容电压更加均衡，证明了本文所采用修正后电容电压排序方法的有效性；CPS-PWM采用了较为复杂的均压控制，其子模块电容电压的均衡程度略微差于NL-PWM，而且控制系统的负担较大。

图15 三种调制策略的仿真结果Fig. 15 Simulation results of the three modulation strategies

5 结 论

本文研究了工作在全电平模式的最近电平逼近PWM(FL-NL-PWM)调制策略，以改善少子模块MMC的运行性能。介绍了该调制策略的工作原理与子模块排序方法，并进行了谐波与环流分析，最后利用MATLAB/Simulink进行了验证，得到如下结论：

(1)通过调整载波的相位可将NL-PWM扩展到全电平模式，相比于基本电平模式，FL-NL-PWM输出电压的电平数目增加，降低了电压的低次谐波畸变率，改善了电流畸变程度；

(2)FL-NL-PWM根据修正后电容电压的排序结果确定子模块工作状态，桥臂中所有子模块共同承担高频PWM开关跳变，实现电容电压均衡，避免子模块开关频率过高；

(3)FL-NL-PWM调制策略采用桥臂电抗器抑制循环电流的高次成分，采用环流抑制策略消除低次成分，循环电流较基本电平模式并无明显变化。