单矢量水听器多维参数联合估计方法
王 进,牛树华
(海装装备审价中心,北京 100071)
近年来,无人艇、UUV、鱼雷等平台技术发展迅猛。对于这些尺寸受限的载体,声呐系统布放的空间资源相对紧张。矢量水听器可以同步获取声场的声压和振速数据,因此,不用成阵仅依靠单个矢量水听器即可实现对目标的方位估计[1-3]。所以,与常规标量探测设备相比,矢量水听器更适合应用于此类平台。
方位估计依赖于信号频率这一先验条件,但实际应用中信号频率通常未知,因此,针对方位频率联合估计问题开展研究具有现实意义。利用矢量水听器获得的声压振速信息,有利于实现对信号方位频率的联合估计。文献[4-7]基于单矢量水听器分别利用ESPIRT算法、波达方向矩阵法和平行因子模型对多个信号的方位角、俯仰角和频率进行了联合估计。但由于算法模型的原因,这三种方法估计的目标数目有限。文献[8-9]分别使用状态空间模型方法和稀疏分解理论获得了单矢量水听器接收信号的方位角和频率参数信息。
在文献[9]的研究基础上,本文提出了基于稀疏分解理论的单矢量水听器多维参数(即频率、方位角和俯仰角)联合估计方法。首先根据声源信号的特征,建立单矢量水听器的时空接收数据模型。然后构造相同形式的过完备原子库,利用稀疏分解理论进行求解,由此可以得到声源信号频率、方位角和俯仰角的精确估计。
1 单矢量水听器时空接收数据模型
假设远场有K个窄带声源信号入射到空间分布的某个三维矢量水听器上,则该单矢量水听器t时刻的接收信号可以表示为
Y(t)=[p(t),vx(t),vy(t),vz(t)]T=
U·X(t)+N(t)
(1)
式中,p(t)表示矢量水听器的声压通道数据,vx(t)、vy(t)和vz(t)分别为矢量水听器的三个振速通道数据;U=[u1,…,uk,…,uK]为4×K维的方向矩阵,其中uk=[1,sinφkcosθk,sinφksinθk,cosφk]T为三维矢量水听器的方向向量,φk和θk分别表示第k个声源的俯仰角和方位角;X(t)为声源信号信息,N(t)为零均值的观测加性高斯白噪声。
对接收信号进行采样,采样点为T个,可以得到:
Y(n)=[p(n),vx(n),vy(n),vz(n)]T=
U·X(n)+N(n)
(2)
式中,n=1,2,…,T-1。根据时空变换技术(TST),将矢量水听器各通道的时域接收数据按每一个采样点进行排列写为式(3)。参照式(3)将式(2)重新整理,如式(4)所示。式(4)中,I是元素全为1的K维列向量,W为观测噪声。为了方便,假设声源信号均为复正弦信号,如式(5)所示。
Y=[p(0),vx(0),vy(0),vz(0),…,p(T-1),vx(T-1),vy(T-1),vz(T-1)]T
(3)

(4)
xk(t)=μkej(2πfkt+σk)+nk(t)=μkejσk·ej2πfkt+nk(t)
(5)
式(5)中,μk、fk和σk为第k个声源信号的幅度、频率和相位,k∈[1,K];nk(t)为高斯白噪声。令E=[μ1ejσ1,μ2ejσ2,…,μKejσK]T,则式(4)可以写为式(6)所示。
(6)
令Fk=[1,ej2πfk,…,ej2πfk(T-1)]T,因此,式(6)可以写为如下形式:
Y=[F1⊗u1,F2⊗u2,…,FK⊗uK]E+W
(7)
式中,⊗为Kronecker积的运算符号;令A=[F1⊗u1,F2⊗u2,…,FK⊗uK],A包含了声源信号的时域和空域信息,称为时空阵列流型。式(7)为单矢量水听器的时空接收数据模型。
2 多参数联合估计方法
首先确定参数的搜索空间,对搜索空间根据精度需求选择合适的间隔进行网格划分。假设频率的搜索点数为Nf个,方位角的搜索点数为Nθ个,俯仰角的搜索点数为Nφ个,则参数搜索空间维度为Ns=Nf×Nθ×Nφ。
假设每个网格点上都存在声源,则式(7)可以改写
成如下形式:
Y=AsZ+W
(8)
其中,
As=[a(f1,θ1,φ1),…,a(fNs,θNs,φNs)]
Z=[z1,…,zNs]T
(9)
式(8)中,a(fi,θi,φi)=Fi⊗ui,i∈[1,Ns];As为4T×Ns维度的矩阵,当4T≪Ns时,As被称为过完备原子库。
但实际上,只有声源真实存在的位置对应的网格点上才有信号,其余网格点上的信号强度为0。所以,Z是个稀疏度为K的稀疏向量,其非零元素的索引包含声源的位置信息。式(8)将单矢量水听器多维参数估计问题转化成欠定线性方程组的求解问题。通常,欠定线性方程组有无穷个解,因此对该方程组的求解需要引入先验性稀疏约束,从而构建稀疏分解模型,如下所示:

(10)
式中,‖·‖0为l0范数,ε为稀疏分解误差容忍项,与数据所含噪声有关。
综上所述,本文提出的单矢量水听器多维参数联合估计方法具体流程归纳如下:
步骤1:将单矢量水听器各通道接收的时域数据选取合适的采样点数参照式(3)进行整理,得到待处理的观测数据Y;
步骤2:确定参数的搜索空间,根据估计精度需求选取合适的间隔对搜索网格进行划分,按照a(fi,θi,φi)=Fi⊗ui的形式构造过完备原子库As;
步骤3:将观测数据Y和过完备原子库As代入式(10),利用正交匹配追踪(OMP)算法进行求解,从而得到稀疏向量Z,将Z中非零元素的索引值进行换算即可获得对参数的估计。
3 数值仿真分析
3.1 方法性能分析
仿真条件1:假设有2个窄带目标源信号入射,幅值分别为2和1,频率分别为32 Hz和80 Hz,方位角分别为83°和227°,俯仰角分别为75°和141°。采样频率为200 Hz。频率搜索范围为1 Hz~100 Hz,搜索间隔为1 Hz;方位角搜索范围为1°~360°,俯仰角搜索范围为1°~180°,搜索间隔均为1°。
基于仿真条件1,使用本文方法进行处理,处理结果如图1所示。

图1 单矢量水听器频率-方位角-俯仰角联合估计结果(2个目标)
由图1a)可知,当信噪比(SNR)为20 dB、快拍数(T)为500时,本文方法可以实现对目标频率、方位角和俯仰角参数的准确估计(本文以单矢量水听器各通道的一个采样点的数据作为一个快拍)。同时,从图中可以得到两个目标信号幅值的估计值分别约等于2和1,与仿真理论值相符。当信噪比下降为5 dB且快拍数仍为500,仿真结果如图1b)所示,此时方位角和俯仰角的估计已出现偏差,但频率估计值仍是准确的。保持信噪比为5 dB,增加快拍数至3 000,仿真结果如图1c)所示,此时方位角和俯仰角的估计值与仿真理论值相符。可以看出,信噪比和快拍数对本文方法的估计性能有重要的影响。
为方便比较,在上文仿真条件1中增加一个新目标:幅值为0.8,频率为65 Hz,方位角为110°,俯仰角为30°。图2展示了3个目标时不同的信噪比和快拍数条件下的仿真结果。对比图2b)和图1b)可知,在同等信噪比和快拍数的条件下,目标数增加会导致方位角和俯仰角估计结果出现误差,频率估计值依旧准确。保持信噪比不变,增加快拍数至5 000,处理结果见图2c)。在该条件下,三个目标源的频率、方位角和俯仰角参数估计都精确。保持信噪比不变,减少快拍数至10,处理结果见图2a)。在该情形下,除了方位角和俯仰角之外,频率的估计值也出现了误差。将图2的三个子图进行比较,可以发现频率估计受快拍数影响较大。
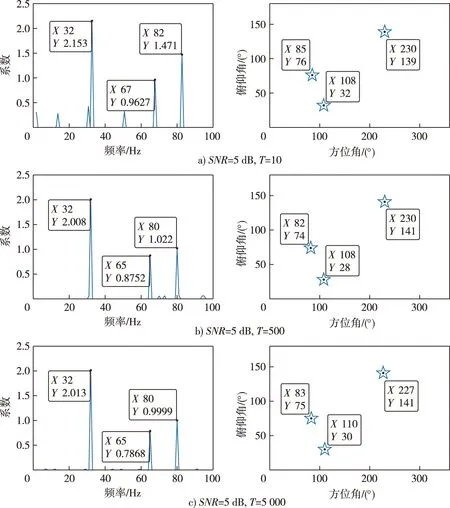
图2 单矢量水听器频率-方位角-俯仰角联合估计结果(3个目标)
3.2 与传统方法对比
仿真条件2:假设有2个目标源信号入射,幅值分别为2和1,频率分别为65 Hz和80 Hz,方位角分别为33°和107°,俯仰角分别为75°和141°。采样频率为200 Hz。为减少计算量,采用变步长的搜索网格。频率搜索范围在64 Hz~66 Hz和79 Hz~81 Hz内时搜索间隔为0.1 Hz,其余搜索间隔为1 Hz;方位角搜索范围在32°~34°、106°~108°,俯仰角搜索范围在74°~76°、140°~142°时,搜索间隔为0.1°,其余搜索间隔为1°。蒙特卡洛试验次数为500。
基于仿真条件2分别使用本文方法和文献[4]中的ESPIRT方法进行处理。使用均方根误差(RMSE)作为衡量标准比较两种方法的估计性能:

(11)

两种方法处理结果如图3和图4所示。图3中展示了固定快拍数为100的条件下,两种方法在不同信噪比时参数估计的RMSE曲线。图4中展示了固定信噪比为10 dB的条件下,两种方法在不同快拍数时参数估计的RMSE曲线。

图3 不同信噪比下参数估计的均方根误差

图4 不同快拍数下参数估计的均方根误差
图3、4中使用本文方法估计频率获得的RMSE曲线分别在15 dB和100个快拍之后截断,原因是在该条件下RMSE的估计值为0,而使用对数坐标系绘制RMSE曲线无法处理0值,因此图中呈现截断状态。由图3、4可知,相比于传统的ESPIRT方法,本文方法对方位角、俯仰角和频率的估计精度更高。
4 结束语
针对单矢量水听器多维参数估计问题,本文提出一种基于稀疏分解理论的单矢量水听器多维参数联合估计方法。通过数值仿真验证了该方法的有效性,同时得出了以下结论:1)目标数、信噪比和快拍数对本文方法的估计性能有重要的影响。目标数越大,维持较高的估计精度需要更大的信噪比或者更多的快拍数;2)相同条件下,本文方法相较于经典的ESPIRT方法估计精度更高。

