房屋顶部刚度突变对结构抗震性能的影响

王同果 王戍

摘  要：建筑顶部设置造型或设备层时，常因其层高较小，侧向刚度较大，造成下部楼层与其刚度比或抗剪承载力之比超规范限值。采用有限元软件分析小震弹性状态下的受力状况和变形特征、以及罕遇地震作用下的弹塑性变形情况，解析房屋顶部刚度突变对结构抗震性能的影响。

关键词：承载力突变;刚度突变;弹塑性变形;薄弱层

中图分类号：TU391.05    文献标识码：A

0 概述

我国89版抗震规范[1]首次提出‘抗震概念设计’的理念，对建筑的平面、竖向的规则性提出要求，其中，对于竖向布置仅提出局部收进不规则定义。2001版抗震规范[2]给出了侧向刚度、承载力突变及竖向构件间断的竖向不规则定义，且规定了不规则的上限，并延续到现行2010版抗震规范[3]，要求结构体系沿竖向布置宜具有合理的刚度及承载力分布，避免因局部削弱或突变形成薄弱部位。

现行2010版抗震规范规定：当楼层的侧向刚度小于相邻上一层的70%，或小于其上相邻三个楼层侧向刚度平均值的80%时;或者楼层的受剪承载力小于相邻上一层的80%时，该楼层为薄弱层。为提高抗震承载能力，实现“大震不倒”的抗震设防目标，抗震设计时，薄弱层的弹性分析地震剪力应乘以不小于1.15的增大系数，《高规》[4]为1.25，必要时要进行大震弹塑性变形分析。

现行建筑设计中，为追求建筑造型，或因功能需要，常在建筑顶部设置高度较小的局部坡屋面或设备间。当其独立成层时，常因其层高较小，侧向刚度较大，致使下部楼层与其刚度比较小或抗剪承载力突变，超出规范限值，对于此种情况是否应按薄弱层进行加强，存在争议。

以实际工程为例，采用satwe空间有限元分析軟件，对实际模型和简化模型分别进行小震弹性分析，对比两种模型地震作用状况下的自震特性、实际受力、变形特征;采用EPDA程序对结构进行大震弹塑性分析，解析结构弹塑性反应直至破坏的全过程，找出结构的薄弱部位，对是否应判定为薄弱层进行探讨。

1 研究对象

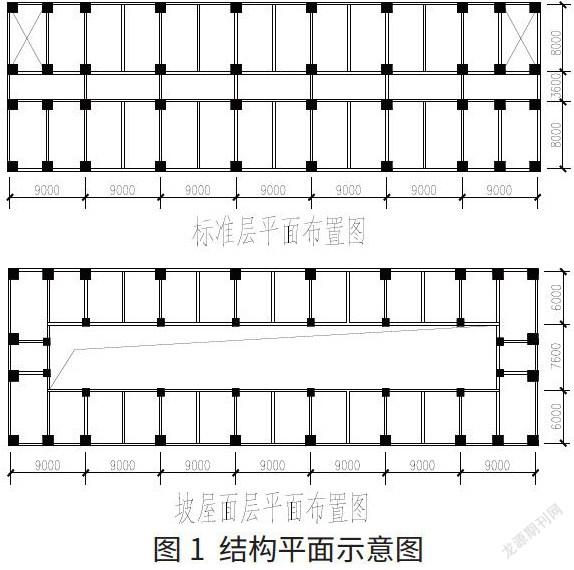
某多层办公楼，地上五层，层高均为4.2m，钢筋混凝土框架结构，因造型需要，屋顶沿外墙周边局部设置坡屋面，高度3.0m。如图1所示为结构平面示意图。

设计参数：抗震设防烈度7度，基本加速度0.1g，设计地震分组为第三组，梁、板、柱的混凝土强度等级均为C30，场地类别Ⅱ类，框架的抗震等级为三级，结构重要性系数为1.0。

2 计算模型

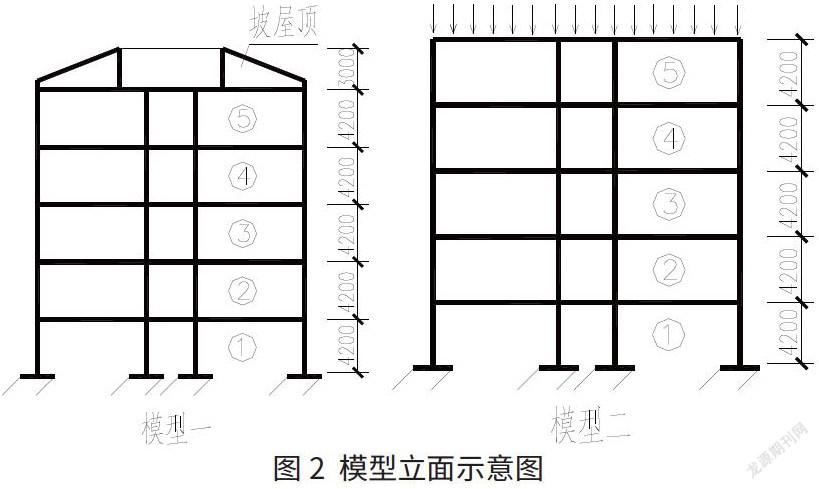
采用两种计算模型进行对比分析：模型一为带坡屋面的实际模型，将坡屋面作为一个楼层对待;模型二为将坡屋面层转化为荷载施加于顶层的简化模型。如图2所示为模型立面示意图。

屋面层相较于其他楼层，抗侧刚度及抗剪承载能力很大，相对变形很小，在满足小震弹性情况下，其大震性能是有保障的。此时把它看作是顶层质量的一部分，忽略其自身承载力而转化为荷载以便对下部楼层进行抗震分析是合理的。

对模型一、模型二进行计算分析，对比自震特性、变形特征，以及弹塑性变形等结构性能，以便对结构的薄弱部位进行判定分析。

3 小震弹性分析

3.1 结构侧向刚度

楼层侧向刚度采用地震剪力与地震层间位移得比算法，刚度比为本层塔侧移刚度与上一层相应塔侧移刚度70%的比值或上三层平均侧移刚度80%的比值中之较小者。

分析结果表明：两种模型各层侧向刚度基本相同;模型一第3、5层刚度比不满足《抗规》要求;模型二各层刚度比均满足规范要求。

3.2 楼层抗剪承载力

两种模型各层抗剪承载力基本相同;模型一第5层抗剪承载力之比不满足《抗规》要求;模型二各层抗剪承载力比均满足规范要求。

3.3 结构自震特性

两种模型计算结果均为：第1振型为平动，第2振阵型为扭转，第3振阵型为平动，且周期基本相同。表明结构自震特性与结构的振型形态基本一致。

3.4 结构变形

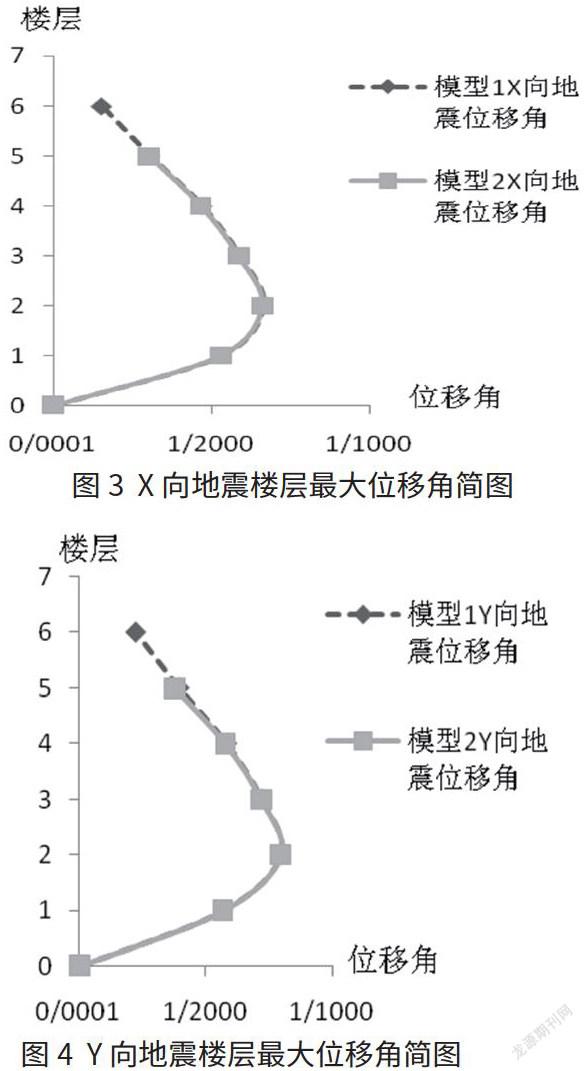
经分析比较：（1）最大楼层位移对比：两种模型楼层变形符合框架结构剪切变形特征，位移曲线走向一致、圆滑、无突变;（2）最大层间位移角对比：最大楼层位移角所在楼层均为2层，X向地震层间位移角均为1/1510，Y向地震层间位移角均为1/1260，且其他各楼层最大位移角基本相同，如图3、图4所示。

4 大震弹塑性分析

采用中国建研院PKPM的EPDA程序进行大震弹塑性分析，分析方法为静力推覆法（push-over），侧推荷载为倒三角形，在X、Y两个方向分别施加。

4.1 模型一分析结果如下

X向加载结果：（1）塑性铰首先出现在4层，在性能点处，柱端产生塑性铰的数量很少，主要分布在2～4层。随着加载步的增加，破坏首先出现在1、2层，且梁先于柱破坏。（2）性能点处，最大层间位移角为1/224，对应的楼层号为第二层，最大有害层间位移角也发生在第二层，如图5所示。

Y向加载结果：（1）塑性铰首先出现在底部1～3层，在性能点处，柱端产生塑性铰的数量很少，主要分布在1～3层。随着加载步的增加，破坏首先出现在1、2层，且梁先于柱破坏。（2）性能点处，最大层间位移角为1/171，对应的楼层号为第二层，最大有害位移角也发生在第二层，如图5所示。

4.2 模型二弹塑性分析

在性能点处，柱端产生塑性铰的数量很少，且进入塑性阶段的时间也比较晚，主要分布在底部楼层处。随着加载步的增加，破坏首先出现在1、2层，且梁先于柱破坏。结果与模型一基本一致。

5 其他对比分析

将模型一第3层层高改为6.0m，进行小震弹性、大震弹塑性计算，并与原模型一计算结果进行对比分析。

5.1 小震弹性分析

分析结果表明：第3、5层刚度比、抗剪承载力之比不满足《抗规》要求，其它层满足要求。

5.2 大震弹塑性分析

X向加载结果：（1）塑性铰首先出现在2、3层，在性能点处，柱端产生塑性铰的数量很少，主要分布在2～3层。随着加载步的增加，破坏首先出现在3层。（2）性能点处，最大层间位移角为1/170，对应的楼层号为第三层，最大有害层间位移角也发生在第三层，如图6所示。

Y向加载结果：（1）塑性铰首先出现在底部2～3层，在性能点处，柱端产生塑性铰的数量很少，主要分布在2～3层。随着加载步的增加，破坏首先出现在3层。（2）性能点处，最大层间位移角为1/143，对应的楼层号为第3层，最大有害位移角也发生在第3层，见图6。

分析结果表明：变形在第3层突变，且塑性铰首先出现在第三层，破坏也始于第三层，表明第3层是真正的薄弱层，而第5层并未表现出薄弱层特征。

另外，通过改变不同位置楼层层高，使层刚度比变化，并进行弹塑性分析。结果表明：当薄弱层位于结构顶部时，变形集中和首先破坏部位均位于结构的底部;当薄弱层位于结构中、下部位时，变形集中和首先破坏部位与薄弱层对应。

6 结语

（1）判断结构竖向的规则性，是以上下楼层之间的侧向刚度和承载力对比为依据，指的是楼层与楼层之间的对比，局部坡屋面层并不是真正意义上的楼层，因此分析软件对坡屋面楼层的计算数据不具有实际意义。

（2）对于结构顶层刚度突变，小震弹性分析结果表明结构变形曲线圆滑，无突变，无薄弱层特征;大震弹塑性分析结果表明：结构的塑性铰分布及出现顺序、变形集中以及破坏部位不与楼层刚度比及抗剪承载力比确定的薄弱层相吻合，可见，顶层刚度突变不影响结构的抗震性能，可不按薄弱层对待。

（3）薄弱层的位置影响结构的承载能力，当薄弱层位于结构顶部时，变形集中位于结构的底部，与无薄弱层的结构基本一致，对结构的承载能力影响不大;当薄弱层位于结构中、下部位时，变形集中和首先破坏部位与薄弱层对应，应加强其抗震承载力。

参考文献

[1] GBJ11-89.建筑抗震设计规范[S].北京：中国建筑工业出版社，1989.

[2] GB50011-2001.建筑抗震设计规范[S].北京：中国建筑工业出版社，2001.

[3] GB50011-2010.建筑抗震设计规范[S].北京：中国建筑工业出版社，2016.

[4] JGJ3-2010.高层建筑混凝土结构技术规程[S].北京：中国建筑工业出版社，2011.

收稿日期：2021-08-08

作者簡介：王同果（1965--），男，山东济南人，本科，工程技术应用研究员，研究方向：土木工程。