“有趣的平衡”教学设计

徐安贵

教学内容：

人教版六年级数学下册第111～112页的内容。

教学目标：

1.通过实验，让学生初步感受杠杆原理，发现反比例关系，加深对反比例关系的理解，探索杠杆原理背后隐藏的数学原理。

2.培养学生的探究意识和归纳概括能力。

3.让学生感受杠杆原理在生活中的应用，增强学生应用数学的意识。

教学过程：

一、利用问题，激发学生的探究兴趣，自制平衡杠杆

同学们听说过“杠杆原理”吗？你知道它在生活中的应用吗？大家可能没想到，杠杆原理的背后隐藏着数学原理，那就是反比例关系。下面就让我们通过实验一起来体验它的奥秘吧。

1.指导学生制作实验用具

师：现在请同学们拿出你们准备好的竹竿和细绳子，同桌合作，把绳子穿进竹竿中心位置的小孔并打结固定好。（教师巡视，对有困难的学生进行指导）

2.检查自制简单杠杆是否合格

师：请同学们握住细绳另一头，拎起你制作的简单杠杆，待竹竿基本稳定时，看看你的竹竿是什么情况。（教师请竹竿平衡的和不平衡的学生各一人上台演示）

你发现了什么？你认为谁制作的更合格？对不平衡的竹竿你知道是什么原因吗？（让学生充分交流，教师再根据实际情况，引导学生对不平衡竹竿进行调整直至平衡）

3.在平衡的竹竿上分节

现在请同学在自制的杠杆上，从中点开始，用你喜欢的方式每隔8厘米做一个记号。（可以刻一个小槽或用彩笔画线等，如果刻小槽，教师要提醒学生注意安全）

设计意图：指导学生制作规范、适用的实验用具是保证本实验成功的前提，其制作标准是：制作完后，提起竹竿中心位置的绳子时，要确保制作的简易杠杆平衡。

二、引导学生合作学习，探究杠杆平衡的规律

现在请同学们拿出你准备的塑料袋和棋子（玻璃球等），然后把塑料袋挂在竹竿左右两边刻度相同的地方，怎样放棋子才能保持平衡？同桌合作，自己放放看。

师：小明在塑料袋里放了3个棋子，挂在竹竿左边离中心点第4个记号处，要使竹竿保持平衡，你要放几个？把塑料袋挂在什么位置？（根据学生的回答，让学生上台展示，教师点拨）

如果左右两边的两个塑料袋任意装入相同数量的棋子，塑料袋移动到什么样的位置竹竿才能保持平衡？自己动手操作看看。（教师巡回指导，对有困难的小组进行点拨）

你发现了什么？（让学生充分交流）

谁来把你的发现告诉大家？（根据学生实验、交流，教师引导学生用自己的话把他们发现的规律抽象概括：不管放的顺序怎样，只要在左右两边相同的刻度处放相同的棋子，竹竿就能平衡）

小结：同学们说得很好，如果塑料袋挂在竹竿左右两边刻度相同的地方，要放相同数量的棋子竹竿才能保持平衡;如果在左右两个塑料袋里装入同样多的棋子，也要把它们移动到离中心点相同的位置杠杆才能保持平衡。

设计意图：本活动是一个操作性很强的实验活动，采用同桌合作的形式让学生自己尝试，教师在关键的地方适当进行指导和点拨，使学生通过具体的棋子数、具体的刻度，通过实验、推理、验证，发现并归纳、总结出特殊条件下竹竿（杠杆）保持平衡的规律。

三、通过探究杠杆平衡规律，体会杠杆原理背后隐藏的数学原理

師：刚才我们探究了当左右两边的塑料袋离中心距离相等，塑料袋里的棋子也相等，竹竿处于平衡状态。现在如果一边的塑料袋在刻度3上，放4个棋子，另一边的塑料袋在刻度4上，你认为放几个棋子才能保持平衡？先猜猜，再具体放放看。（教师巡视，对有困难的学生适当进行点拨）

如果左边塑料袋在刻度6上放1个棋子，右边塑料袋在刻度2上放几个棋子竹竿才能平衡？在刻度3上呢？先说说，再想想，最后动手验证。

你发现了什么？（教师引导学生抽象概括出：要使竹竿保持平衡，必须使“左边的刻度×棋子数=右边的刻度×棋子数”的结论）

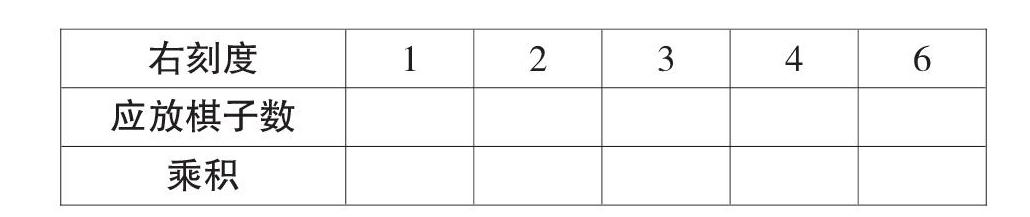
现在老师把装有4个棋子的塑料袋放在左边刻度3上并保持不变，你觉得在右边各个刻度上的塑料袋里放几个棋子，竹竿才能平衡？有几种放法？把你的放法和同学们分享，并说说你是怎样想的？并把结果记录下来。（教师用多媒体出示表格）

你发现了什么？（如果左边刻度3处放4个棋子并保持不变，右边的刻度数×棋子数的乘积是12，竹竿就会保持平衡）

你发现表中的刻度数和所放棋子数成什么比例关系？为什么？（引导学生有序思考，并抽象概括出：当左边的刻度数和棋子数保持不变时，如果竹竿平衡，右边刻度数和棋子数成反比例，因为刻度数×棋子数=一个常数“12”）

设计意图：在探究规律时，要在适当的时候引导学生从具体上升到抽象，从特殊情况过渡到一般情况。教学时，通过引导学生经历从特殊到一般的研究过程，培养学生的探究意识和归纳概括能力;通过实验，让学生初步感受杠杆原理，体会反比例关系，加深对反比例关系的理解。

四、结合实际，体会杠杆原理与生活的联系

同学们，在我们的生产生活中，很多地方都利用了我们今天探究的有趣的平衡（杠杆原理）。我们经常玩的跷跷板，有时候能够达到左右平衡，就是应用我们今天探究的杠杆原理。请同学们打开课本，认真阅读第112页最下面的“生活中的数学”，体会竹竿的平衡与这两个实例内在的联系。

你还知道哪些生活中应用了杠杆原理的例子？请你具体说一说。

2190年前，古希腊出现了一位伟大的物理学家阿基米德，他说：“只要给我一个支点，我就能撬起整个地球。”他一生勤奋好学，刻苦钻研，人民利用他发现的杠杆定律设计了多种机械，为人民、为祖国服务。你理解阿基米德“只要给我一个支点，我就能撬起整个地球”这句话的意思吗？课后查阅阿基米德的相关资料进一步了解。

设计意图：通过“生活中的数学”的学习，让学生进一步感受杠杆原理在生活中的应用，体会生活中处处有数学，增强学生学好数学、应用数学的意识。