醇及脱氧核糖与水分子间三体作用强度的快速准确计算
李晓蕾,孙云娇,唐 颖,王长生
(辽宁师范大学化学化工学院,大连116029)
生物分子与水分子间的氢键协同效应对水环境中蛋白及DNA的分子结构和性质有重要影响.多体极化作用是氢键协同性的主要来源,快速准确计算多体极化作用强度对提升分子模拟方法的准确性十分重要[1~3].
Xantheas等[4~6]发现,三体作用对水团簇稳定性的影响可高达30%,四体及以上多体作用的贡献可被忽略.对甲烷水复合物CH4(H2O)2和CH4(H2O)20的研究表明,三体作用对结合能的贡献不可忽略[7].Paesani等[8,9]通过评估团簇H3O+(H2O)n和OH−(H2O)n的多体作用强度发现,体系的总相互作用能主要由二体和三体作用贡献.杨微等[10]使用高精度从头计算方法计算了团簇(H2O)n(n=8,10,16,20,22,24)的二体、三体和四体作用能,发现三体作用对总作用能的贡献可高达25%,四体作用在总作用能中所占的比例不超过3%,五体及以上多体作用在总作用能中所占的比例不超过0.5%.对67个不同尺寸水团簇总三体作用能的计算结果表明,由30个水分子构成的团簇的总三体作用能可高达−209.87 kJ/mol[11].李书实等[12]对酰胺、二肽、尿嘧啶与水分子形成的氢键复合物的三体效应的研究表明,三体作用能占体系总作用能的10%~20%.以上研究结果表明,含水体系中的三体作用能对体系稳定性有重要影响.
使用高精度从头计算方法可以准确计算得到三体作用能.但是由于三体作用数目随体系中分子数目的增多而急剧增大,致使使用高精度从头计算方法计算三体作用能变得十分昂贵.以水分子团簇为例,对于含有10个水分子的体系,共计有120个三体作用;当体系中水分子的个数增加到30个时,三体作用数目急速增加到4060个.因此,发展一种能够快速准确计算氢键复合物体系三体作用强度的方法变得十分重要[13].
在蛋白质水体系中,极性氨基酸侧链可与水分子形成具有不同氢键网络结构的团簇.这些团簇中存在大量的三体作用,并对生物分子的稳定性产生重要影响.丝氨酸和苏氨酸的侧链均含有一个羟基,与甲醇(CH3OH)和乙醇(CH3CH2OH)的结构相类似.本文使用甲醇、乙醇与水形成的氢键复合物来模拟丝氨酸和苏氨酸侧链与水分子间的作用,使用高精度的量子力学(QM)方法和可极化偶极-偶极作用模型计算体系中的三体作用能.通过拟合甲醇与水氢键复合物三体作用能随分子间距离变化的能量曲线确定了可极化偶极-偶极作用模型所需的参数.将可极化偶极-偶极作用模型和所确定的参数应用于快速预测更多的甲醇、乙醇与水氢键复合物以及脱氧核糖与水氢键复合物的三体作用能,检验了模型的准确性和参数的可转移性.
1 研究对象和计算方法
1.1 研究对象
使用二阶微扰理论的MP2/6-31+G(d,p)方法优化得到了1个甲醇分子与2个水分子构成的氢键三聚体CH3OH·(H2O)2、2个甲醇分子与1个水分子构成的氢键三聚体(CH3OH)2·H2O、3个甲醇分子构成的氢键三聚体(CH3OH)3、1个乙醇分子与2个水分子构成的氢键三聚体CH3CH2OH·(H2O)2、2个乙醇分子与1个水分子构成的氢键三聚体(CH3CH2OH)2·H2O、3个乙醇分子构成的氢键三聚体(CH3CH2OH)3和1个脱氧核糖分子与2个水分子构成的氢键三聚体C4H9O3CHO·(H2O)2的稳定几何构型.采用常温常压(NPT,p=101.325 kPa,T=298 K)系综进行分子动力学模拟,得到了1个甲醇分子与20个水分子构成的团簇CH3OH·(H2O)20、1个乙醇分子与20个水分子构成的团簇CH3CH2OH·(H2O)20和1个脱氧核糖分子与12个水分子构成的团簇C4H9O3CHO·(H2O)12的随机结构.团簇获取过程如下:将CH3OH,CH3CH2OH和C4H9O3CHO对应放入边长为1.5,1.7和2.1 nm的立方水盒子中,分别在NPT(p=101.325 kPa,T=298 K)系综下进行2 ns的分子动力学模拟,步长均设置为1 fs,分别随机选取了2 ns时CH3OH及其距离最近的20个水分子、1 ns时CH3CH2OH及其距离最近的20个水分子和800 ps时C4H9O3CHO及其距离最近的12个水分子,依次得到了团簇CH3OH·(H2O)20,CH3CH2OH·(H2O)20和C4H9O3CHO·(H2O)12的结构.
1.2 QM方法
在n个分子所构成的多聚体中,由第i,j,k个分子所构成的三聚体的三体作用能(V3B,kJ/mol)定义如下[14]:
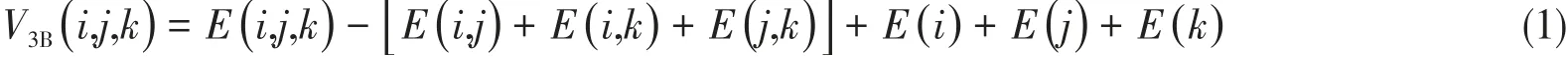
总三体作用能(IE3B,kJ/mol)为体系中所有三体作用能之和[15],即

式中:E(i,j,k)(kJ/mol),E(i,j)(kJ/mol)和E(i)(kJ/mol)分别为三聚体、二聚体和单体的能量.所有甲醇、乙醇与水氢键复合物的三聚体、二聚体和单体的能量均由包含基组重叠误差校正[16]的MP2/aug-ccpVTZ方法计算获得,脱氧核糖与水氢键复合物的三聚体、二聚体和单体的能量均由包含基组重叠误差校正的MP2/aug-cc-pVDZ方法计算获得.全部计算均使用Gaussian 09[17]程序包完成.
1.3 基于可极化偶极-偶极作用模型计算三体作用能
根据可极化偶极-偶极作用模型(PBFF)[18,19],对于由n个单体构成的体系,极化作用对体系总能量的贡献[Epol(1,···,n),kJ/mol]可表示为
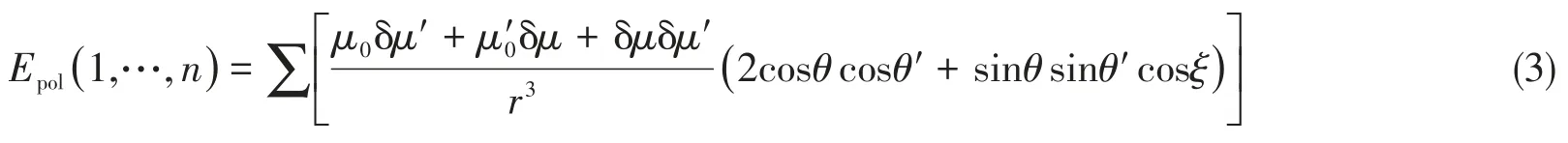
式中:δμ=μ−μ0为某化学键的诱导偶极矩;μ(C·m)为团簇或复合物体系中单体的某个极性化学键的键偶极矩;μ0(C·m)为该单体处于孤立状态时的这个极性化学键的键偶极矩;μ0,δμ和μ′0,δμ′分属于不同的单体分子.θ,θ',ζ,r是与两个键偶极相对位置有关的几何参量[20].式(3)的求和遍及不同单体间所有偶极-偶极作用.
对于孤立分子,不存在环境或其它分子对它的影响,式(3)变为

对于由单体i和j两个分子构成的体系,可以将一个分子看成为另一个分子的环境,对i,j两个单体间的所有偶极-偶极作用求和后,将得到两个分子间的极化作用Epol(i,j).同理,对i,j,k3个单体间的所有偶极-偶极作用求和后,将得到3个分子间的极化作用Epol(i,j,k).
所以,可极化偶极-偶极作用模型下的三体作用能的计算如下:

诱导偶极矩δμ使用下式计算:

式中:q0(C)为孤立分子的原子分数电荷;q(C)为复合物中相对应的原子分数电荷;d(nm)为化学键的键长;由于不同理论计算方法计算的原子分数电荷与其真实值间存在差异,为了得到与真实值更为接近的理论计算结果,在式(6)中加入了电荷修正系数c,其数值依赖于计算原子分数电荷时所使用的方法,c的值应≥0.c>1表示计算原子分数电荷所用的方法低估了复合物与孤立分子中原子分数电荷的差异,c<1则表示方法高估了复合物与孤立分子中原子分数电荷的差异.
1.4 参数的确定
使用可极化偶极-偶极作用模型计算体系的三体作用能需已知θ,θ',ζ,r,d,q0,q,μ0和c等9个量,其中,θ,θ',ζ,r,d的值可通过体系中原子的坐标计算得到,q和q0由AM1方法计算获得.对于本文所研究的醇-水体系,水分子的O—H键偶极的固有偶极矩μ0和电荷修正系数c直接沿用我们前期工作确定的值,即μ0(O—H)=5.04×10−30C·m[21],c=1.86[22].甲醇分子含有3种化学键,分别是极性较强的C—O和O—H键以及弱极性化学键C—H键,乙醇分子较甲醇分子多一个非极性化学键C—C键.本文中忽略非极性化学键C—C键和弱极性化学键C—H键的键偶极矩,醇分子中的O—H键的固有偶极矩参数和电荷修正系数取值与水分子的相同.因此只需要确定极性化学键C—O的固有偶极矩参数和电荷修正系数.
C—O键的固有偶极矩参数μ0和电荷修正系数c的确定方法如下:选取如图1所示的(CH3OH)2·H2O氢键复合物为模型分子,在参与形成氢键的两个O原子中心设置一个虚原子,改变虚原子与另一个O原子间的距离R,分别使用包含基组重叠误差校正的MP2/aug-cc-pVTZ方法和本文方法计算不同距离R所对应结构的三体作用能,可获得三体作用能随分子间距离变化的能量曲线.调整C—O键的参数μ0和c的值,直至采用本文方法计算的三体作用能随分子间距离变化的能量曲线与MP2/aug-cc-pVTZ方法计算结果的误差最小,从而确定了醇分子C—O键的固有偶极矩参数μ0(C—O)=6.67×10−30C·m和电荷修正系数c(C—O)=0.根据式(6),c的值为0意味着不考虑C—O偶极的极化.

Fig.1 Structures of the trimers in training set
2 结果与讨论
2.1 三体作用能及其随分子间距离变化的计算
为了检测可极化偶极-偶极作用模型的准确性和参数的可转移性,将其应用于计算甲醇、乙醇和脱氧核糖与水氢键复合物的三体作用能.图2为由MP2/6-31+G(d,p)方法优化得到的甲醇、乙醇和脱氧核糖与水分子形成的三聚体的稳定结构,其中结构A~C为CH3OH·(H2O)2,结构D和E为(CH3OH)2·H2O,结构F为(CH3OH)3,结构G为CH3CH2OH·(H2O)2,结构H为(CH3CH2OH)2·H2O,结构I为(CH3CH2OH)3,结构J和K为C4H9O3CHO·(H2O)2.
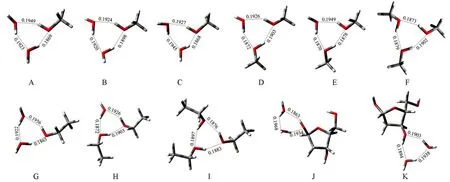
Fig.2 Structures of trimers in testing set
由图2可知,CH3OH·(H2O)2的3个异构体之间和(CH3OH)2·H2O的2个异构体之间的结构既相似又略有不同,相似点在于,这些三聚体均形成3条氢键,且氢键键长差别不大;不同点在于,甲醇分子中的—CH3和水分子中未参与形成氢键的H原子取向存在一定差异.从图2还可见,这11个三聚体中,每个三聚体均形成3条O—H…O型氢键,且每个分子既作质子供体,又做质子受体,因此推测体系的三体作用将表现为吸引,即三体作用能小于零.
表1 列出了使用MP2/aug-cc-pVTZ方法计算的甲醇-水三聚体和乙醇-水三聚体的三体作用能以及使用MP2/aug-cc-pVDZ方法计算的脱氧核糖-水三聚体的三体作用能.为了比较,表1还给出了PBFF的计算结果.
从表1可见,这11个三聚体的三体作用能均为负值,即三体作用表现为吸引,与我们的推断一致,即,当所有分子既作氢键供体又作氢键受体时,体系表现协同性;对比6个甲醇-水三聚体(A~F)的三体作用能,发现三体作用强度随三聚体中所含甲醇数目的增多而增强,对比3个乙醇-水三聚体(G~I)的三体作用能也可得到类似的结论.
比较MP2方法和PBFF模型计算的三体作用能,可见PBFF模型计算的三体作用能与MP2方法结果的最大绝对误差(Maximum absolute error)出现在三聚体H,即(CH3CH2OH)2·H2O,使用MP2/aug-ccpVTZ方法计算该三聚体的三体作用能为−10.25 kJ/mol,PBFF模型计算的结果为−8.87 kJ/mol,两种方法结果间的误差仅为1.38 kJ/mol;对于这11个三聚体的三体作用能,两种方法计算结果的均方根误差(Root-mean square error)为0.77 kJ/mol.以上结果说明,PBFF模型较好地预测了这11个三聚体的三体作用能.
为了验证PBFF模型对甲醇、乙醇和脱氧核糖与水氢键复合物不稳定结构的适用性,将其应用于计算甲醇-水、乙醇-水和脱氧核糖-水三聚体的三体作用能随分子间距离变化的能量曲线.
对甲醇、乙醇与水分子形成的三聚体,在参与形成氢键的两个O原子中心放置一个虚原子,改变虚原子与另一个O原子间的距离(R),计算三体作用能,可得到三体作用能随分子间距离变化的能量曲线(图3).对脱氧核糖与两个水分子形成的三聚体,在两个水分子的O原子的中心设置一个虚原子,分别改变脱氧核糖分子中参与形成氢键的O原子与两个水分子中O原子的距离以及与虚原子间的距离,可得到三组三体作用能随分子间距离变化的能量曲线(图4).

Table 1 Three-body interaction energies(IE3B)calculated by different methods for the testing trimers A—K in Fig.2
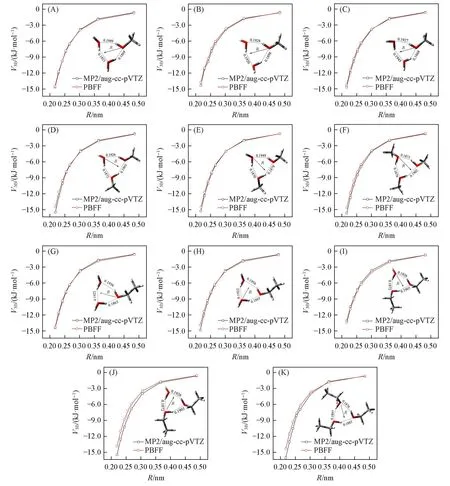
Fig.3 Three⁃body interaction energy(V3B)vs.the intermolecular distances(R)for the testing trimers A—I

Fig.4 Three⁃body interaction energy vs.the intermolecular distances for the testing trimers J and K
由图3可知,对于甲醇-水三聚体和乙醇-水三聚体而言,三体作用能随分子间距离变化的能量曲线存在一定的相似性,即,当分子间距离R介于0.21~0.48 nm之间时,三体作用能介于−16.00~−0.50 kJ/mol之间.综合图3和图4可知,对甲醇、乙醇和脱氧核糖与水分子形成的三聚体而言,随着分子间距离R的变大,三体作用强度逐渐减弱,由此可推测,三体作用为近程作用;PBFF模型计算得到的能量曲线不仅较好地描述了三体作用能随分子间距离变化的趋势,而且模型得到的三体作用能与MP2方法的计算结果符合得很好,说明PBFF模型可准确预测三体作用能随三聚体结构的变化,进一步验证了PBFF模型的准确性.
2.2 团簇体系总三体作用能的计算
相较于三聚体,甲醇、乙醇、脱氧核糖与多个水分子形成的团簇的结构和性质与分子存在于水溶液中的情况更为接近.为了进一步验证模型的准确性,将PBFF模型应用于计算CH3OH·(H2O)20,CH3CH2OH·(H2O)20和C4H9O3CHO·(H2O)12的总三体作用能,为了比较,还给出了AMOEBAbio18方法的计算结果,其中AMOEBAbio18方法的结果使用Tinker程序包计算得到.图5为这3个团簇的结构图.表2列出了采用MP2方法、AMOEBAbio18方法和PBFF模型计算的总三体作用能结果,其中,第4列为以MP2结果作为基准,AMOEBAbio18方法计算结果的误差(Δ),第6列为以MP2结果作为基准PBFF模型计算结果的误差(Δ).
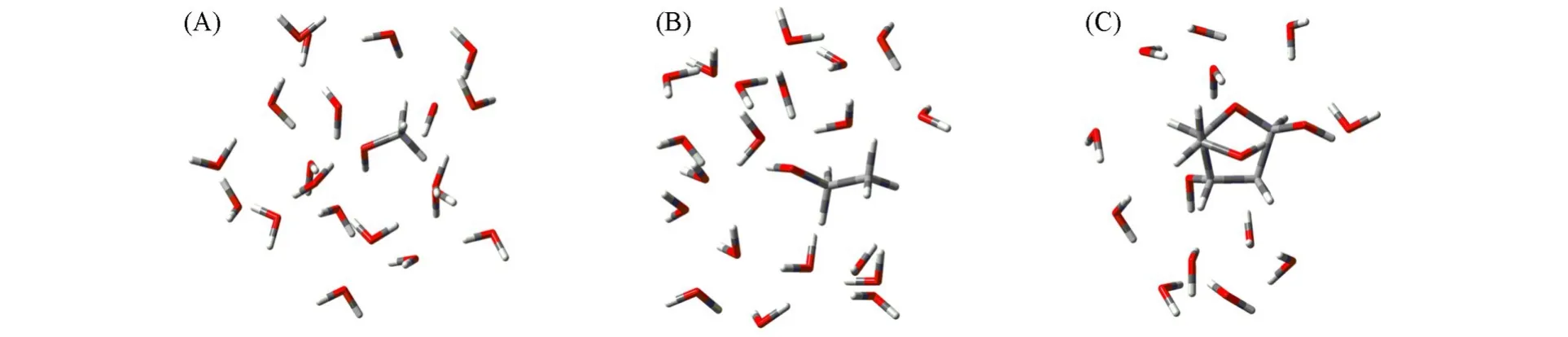
Fig.5 Structures of CH3OH·(H2O)20(A),CH3CH2OH·(H2O)20(B)and C4H9O3CHO·(H2O)12(C)

Table 2 Total three-body interaction energies(IE3B)calculated by different methods
由表2可知,对于团簇CH3OH·(H2O)20和CH3CH2OH·(H2O)20,使用MP2/aug-cc-pVTZ方法计算的总三体作用能分别为−59.25和−35.82 kJ/mol,使用AMOEBAbio18方法计算的总三体作用能分别为−55.52和−27.51 kJ/mol,误差分别为−3.73和−8.31 kJ/mol,使用PBFF模型计算的总三体作用能分别为−59.41和−35.86 kJ/mol,误差仅为0.16和0.04 kJ/mol;对于团簇C4H9O3CHO·(H2O)12,使用MP2/aug-cc-pVDZ方法计算的总三体作用能为−7.15 kJ/mol,使用AMOEBAbio18方法计算的三体作用能为−8.42 kJ/mol,误差为1.27 kJ/mol,使用PBFF方法计算的总三体作用能为−6.57 kJ/mol,误差仅为−0.58 kJ/mol.上述结果说明,对于这3个大尺寸团簇,PBFF模型计算的总三体作用能与MP2方法的计算结果符合得很好,模型的计算精度优于AMOEBAbio18方法,进一步证明了模型的准确性.
3 结 论
对于醇分子,仅考虑极性较强的C—O和O—H键的键偶极矩,忽略非极性化学键C—C键和弱极性化学键C—H键的键偶极矩,通过拟合甲醇水三聚体的三体作用能,确定了可极化偶极-偶极作用模型所需参数.将模型及参数应用于计算更多的甲醇、乙醇和脱氧核糖与水氢键复合物的三体作用能及其随分子间距离变化的能量曲线.计算结果表明,可极化偶极-偶极作用模型和本文所确定的参数可准确预测具有不同结构三聚体的三体作用能以及较大团簇的总三体作用能,计算精度与MP2方法的精度相当.目前,可极化偶极-偶极作用模型已经可以准确地预测水团簇的三体作用强度、醇及脱氧核糖与水分子间的三体作用强度,期望为准确快速模拟水环境中蛋白质和核酸的结构和性质提供有力的工具.

