基于多尺度自回归模型体系的混凝土坝位移预报及工程应用

陈良捷,魏博文,2,喻俊豪,罗绍杨,毛 颖

(1.南昌大学 建筑工程学院,南昌 330031;2.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,南京 210098)

1 研究背景

大坝位移是坝体结构变形效应的具体表现之一，也是综合评判大坝服役健康状况的重要指标[1]。位移监测序列反映了坝体结构在多元复杂环境驱动作用下的动态演变过程，故对大坝位移原型监测资料进行信息挖掘并建立精确可靠的数学模型是现阶段大坝安全监控领域中的重要研究方向，也是保障大坝安全运行的必要依据之一[2]。混凝土坝位移效应量不仅受到库水压力和坝体温度的主要影响，还受到渗流、施工工艺、坝体裂缝、地基以及时效等内外双重环境因素的次要影响。这使混凝土坝位移监测数据普遍遭受复杂噪声污染并呈现强非线性和不规则混沌特性[3-4]。因此，混凝土坝原型监测资料中混沌信号的分析技术研究以及服务于坝体结构监测的实时预报模型构建，对及时掌握大坝服役性态和维护大坝长期安全运行具有重要意义[5-7]。

随着对大坝原型观测资料中混沌特性的深入认识和数学技术手段的迅猛发展，国内外学者通过对能直观映射坝体结构行为的变形监测时序进行分析研究，提出了许多基于信息科学发展和机器学习创新的混凝土坝变形数值模型，例如支持向量机[8]、BP神经网络[9]、极限学习机[10]、灰色系统理论[11]、遗传优化算法[12]等。然而，现有研究在应用数学技术建模进行大坝位移预报时，对于效应量与其影响因子之间的复杂非线性关系及不确定信息因素影响等方面考虑欠佳，进而限制了数值模型的拟合精度与预报结果可靠性的提升。因为很多不确定信息因素都是客观存在的且影响着效应量的波动变化[13]，所以如何有效提取大坝位移监测序列中的混沌成分以充分发掘次要环境影响信息，从而更全面地展示效应量与环境量之间的响应关系，对提高预报模型的计算精度具有重要意义。

据此，针对主次要环境驱动对大坝位移效应存在的交叉影响致使监控模型计算精度降低的问题，本文引入多尺度小波重构技术，将观测时序在频域空间中划分为具有明显趋势性的系统信号及高频非线性的细节信号，并鉴于其信号特征分别融入ARIMA模型和NARX模型进行组合计算，在此基础上建立了基于多尺度自回归模型体系的混凝土坝位移预报模型。以某工程实例参与计算并结合相关统计评判指标，验证了所建组合模型的可靠性和科学性，从而更加真实地反映大坝的服役性态和健康状况。

2 混凝土坝位移监测时序的多尺度小波预处理

小波技术是基于应用数学创新的新型时频多分辨率分析方法，在时频领域皆能刻画信号的局部特征[14-16]。通过改变平移因子和伸缩因子致使小波基发生变换，对原始信号进行分层次地挖掘多尺度信息，具有较低频率分辨率和较高时间分辨率的高频部分往往存在非线性复杂信息，其重要程度虽不及低频主流部分，但也是信号精确表征中不可或缺的一部分。

混凝土坝位移是库水压力、温度、渗流、施工、地基、周围环境以及时效等诸多因素协同驱动的结果[17]。在混凝土坝位移监测时序中，由于环境驱动的主次占比程度以及不确定的仪器量测精度等因素影响，存在着低频系统信号和高频细节信号。系统信号具有明显的趋势性和周期性，代表着库水压力和温度的主流影响；细节信号的非线性混沌特征较为突出，随机性较强，代表着混凝土坝服役期间坝体及坝基材料参数演变、坝体内部结构损伤、节理裂隙、流固耦合以及现场量测误差等不确定的未知次生因素影响[18]。假设混凝土坝位移监测时序为δo(t)，小波分解预处理过程如图1所示。

图1 小波分解示意图Fig.1 Schematic diagram of wavelet decomposition

由图1所示，混凝土坝位移监测信号δo(t)经小波逐次分解得到末层系统信号A3及各层细节信号D1、D2、D3，则混凝土坝位移原型观测信号在分解尺度G下的数学表达式为

(1)

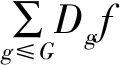
3 基于自回归模型体系的位移组合预报机制

3.1 基于NARX模型的细节信号处理

NARX模型是基于线性自回归模型提出的一种非线性有源网络结构，是一种典型的动态循环神经网络，由时延层、输入层、隐含层和输出层组成[19-21]。时延层将模型的输出进行延迟处理后反馈到输入层，给网络计算增添动态特性以提高预测效果。输入层对输入数据进行集中赋权和阈值运算，再将结果传递给隐含层。隐含层负责接收数据且继续进行连接权值和阈值的运算，最终传递给输出层[22-25]。隐含层的计算表达式为

a=1,2,…,l。

(2)

式中：δa为隐含层的计算结果；f为隐含层的非线性传递函数；n为输入神经元的个数；xi为神经网络的外部输入;wia为外部输入部分与隐含层之间的连接权值，i=1,2,…,n；δs为神经网络的输出反馈；wsa为输出反馈部分与隐含层之间的连接权值，s=1,2,…,m；λa为隐含层阈值；l为隐含层神经元个数。

输出层将传递过来的计算输出与期望输出进行比较，得到误差值。

(3)

ek=ok-δk。

(4)

式中：δk为输出层的计算结果；g为输出层的非线性传递函数；u为输出神经元的个数;l为隐含层神经元个数；wak为隐含层与输出层之间的连接权值，a=1,2,…,l；λk为输出层阈值；ok为期望输出;ek为期望输出与计算输出之间的误差。

再反向修正权值、阈值以及传播输出数据：

(6)

图2 NARX模型结构示意图Fig.2 Schematic diagram of NARX structure

NARX模型能够将输出信号反馈到输入端，从而将输出信号参与到下一次的迭代训练中，具有长期记忆功能，因此能更好地描述具有复杂映射关系的时变系统特性，实现非线性映射的多层前向神经网络与可描述动态系统的回归网络相结合，能够有效模拟非线性过程[26]，处理高频非平稳的监测信号，使其未知效应驱动得到真实诠释，提高计算模型的拟合与预报的可靠性和准确性。

3.2 基于ARIMA模型的系统信号处理

ARIMA(p,d,q)模型是一种基于随机理论的时间序列分析方法，用于表征预测对象的延续发展并综合分析时序的过去值和现在值以预报其未来值[27]。其建模思想是针对于非平稳时间序列δt，经过d阶逐层差分后成为平稳序列，再将此平稳时序代入ARIMA(p,q)模型进行拟合计算，最后结果通过逆变换方式转化为原序列形式[28-29]。ARIMA(p,d,q)模型数学表达式为

(7)

ARIMA(p,d,q)模型建成与运行需进行3个步骤。

当差分处理阶数d=1时，

(8)

当差分处理阶数d=2时，

(9)

(2)模型识别定阶：采用样本序列自相关函数(Auto Correlation Function,ACF)和偏自相关函数(Partial Auto Correlation Function,PACF)的图形截尾拖尾识别以大致确定模型中自回归阶数p和移动平均阶数q；同时为了避免图形识别的主观性影响以及模型过拟合问题，综合贝叶斯信息准则(Bayesian Information Criterion,BIC)进行最终模型定阶，BIC准则的数学表达式为

BIC=klnn-2lnL。

(10)

式中：k为模型参数数量；n为样本数量，L为似然函数。相比于赤池信息准则(Akaike Information Criterion,AIC)，BIC准则增加了样本数量的惩罚项，更加适合样本量较大的混凝土坝位移监测信号。

(3)参数估计与诊断分析：通过拟合计算出备选模型ARIMA(p,d,q)中各项自回归和移动平均的待估参数，初步确立模型方程；为了进一步确定模型的合理性和可取性，还需进行参数的显著性检验和残差的随机性检验。

3.3 NARX-ARIMA混凝土坝位移组合预报模型的构建

综合上述2种针对不同频域特征的监测信号对象所采取的数学建模方案，构建了基于多尺度自回归模型体系的混凝土坝位移组合预报模型，模型结构流程如图3所示。

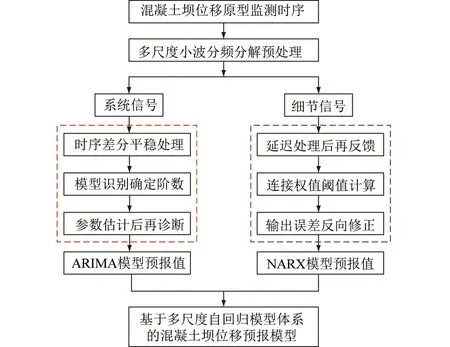
图3 组合模型的构建流程Fig.3 Flowchart of combinatorial model

首先对混凝土坝位移原型监测时序进行多尺度小波分频分解预处理，再分别使用ARIMA模型和NARX模型对其系统部分及细节部分建模计算，最后将其仿真结果进行有机叠加。同时对组合模型进行效果评估以验证其计算有效性，本文引入统计学领域中衡量精准度的评判指标：平均绝对误差(Mean Absolute Error,MAE)、均方误差 (Mean Square Error,MSE)、平均绝对百分误差(Mean Absolute Percentage Error,MAPE )以及决定系数(Coefficient of Determination,R2)。其表达式分别为：

(11)

(12)

(13)

(14)

4 工程应用

某混凝土坝位于福建省永定县境内，最大坝高113.0 m，坝顶高程179.0 m，正常蓄水位为173.0 m，总库容为20.35亿m3，属大(1)型水利枢纽工程。为了精准监测混凝土坝的位移效应，该坝布置了正垂线、倒垂线、引张线和视准线等变形观测设备，其中平行和垂直于坝轴线的位移量采取垂线监测方式，具体布置方案如图4所示。

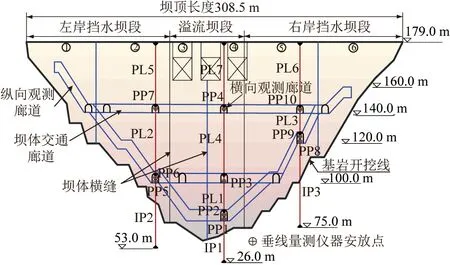
图4 大坝垂线监测系统布置Fig.4 Layout of dam’s vertical line monitoring system

本文选取该混凝土坝第4号坝段的正垂线测点PL4水平位移自动化监测时序为研究对象，建模拟合时间为2018年1月1日至2019年11月30日，时间步长统一化后剔除异常干扰值，并以计算时序首日为参照进行相对化处理，得到包含699组数据的混凝土坝位移实测序列，作为组合模型的训练样本。同时选取2019年12月1日至2019年12月31日的31组实际数据与组合模型预报值进行对比以检验模型的可靠性。

针对混凝土坝位移监测时序的多频域交叉影响，采用小波技术对其进行分解与重构。在小波分解重构过程中，需选定小波函数及分解层数。Daubechies小波函数与尺度函数的有效支撑长度为2N-1，消失矩阶数为N，且其函数具有正交性和紧支性，相比常见Haar小波和Morlet小波具有更有效的综合分析能力。信号频率划分的细致程度取决于小波分解层数，分解阶次愈多，消失矩阶数愈大，频带划分效果愈好，信号逼近的平滑性和稳定性愈好，但是会使时域紧支撑性减弱，分解操作的计算量增加，实时性变差，较强的分解力度也会导致信号中的有用信息在分解过程中流失，操作误差也随之增大，从而间接造成组合模型的预测精度下降。因此，综合考虑监测序列的时频特征及研究领域的通用情况，选用db4小波基对训练样本进行5层分解，分解得到的系统信号及细节信号如图5所示，即δo=A5+D5+D4+D3+D2+D1。

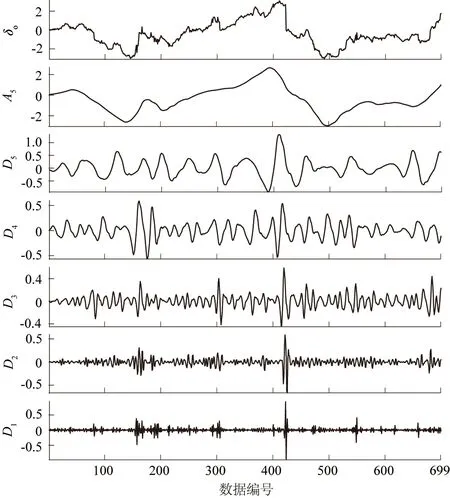
图5 组合模型训练样本的小波分解与重构Fig.5 Wavelet decomposition and reconstruction of training samples of combinatorial model

随着小波分解层数增大，较低频的细节信号也将被逐步从系统信号中剥离出来。将小波5层分解出来的细节信号相互叠加，便得到最终细节信号。为解除高低频数据之间的复杂影响，将混凝土坝位移监测时序分解为高频细节信号和低频系统信号再分别进行建模计算，信号特征如图6所示。

图6 混凝土坝位移时序的系统信号和细节信号Fig.6 System signal and detail signal of displacement sequence of concrete dam

由图6可知，系统信号的变化趋势相比细节信号更加贴近原始信号，原因是系统信号代表着库水压力、温度等主流已知环境因素的影响，具有一定规律性和稳定性，而细节信号代表着大自然中未知的环境驱动以及不确定的时效作用，因此对细节信号的深度挖掘利用是提高组合模型预报精度的关键。

本研究将699组训练样本及31组测试样本的细节部分皆引入NARX模型中，其中669组作为训练集，30组作为验证集，31组作为测试集；隐藏层神经元个数为10，延迟阶数为2；训练方案选取贝叶斯正则化算法，该算法以牺牲计算效率为代价，能更好地完成复杂或者混乱的信号学习；同时依据大坝安全监控经典理论[30]的回归公式(式(15))选取相关环境因子参与建模计算，NARX模型计算结果如图7所示。

图7 NARX模型的计算结果Fig.7 Calculation result of NARX model

+c1(θ-θ0)+c2(lnθ-lnθ0) 。

(15)

由图7(a)可知，NARX模型在训练13次后验证集的误差开始上升，证明网络训练可以结束，此时样本误差值为0.007 826；由图7(b)和图7(c)可知，误差在滞后数为0时最大，且其他情况皆不超过置信区间，同时输出样本与误差的相关系数皆在0刻度线附近，说明该数值模型具有可靠性和科学性；通过图7(d)可知，训练集、验证集、测试集的计算效果较佳，表明基于混凝土坝位移监测时序细节部分的NARX模型成功建成，其具体拟合预测结果及计算误差如图8所示。

图8 细节信号的拟合预测及误差Fig.8 Results of fitting,prediction and error of detail signal

从图8可知，实测值和计算值在拟合及预测时间内变化趋势大致相同，误差也在0刻度线附近，平均误差值为0.094 4。综上表明细节信号模型的计算精度满足实际需要。对于表征库水压力、温度等主流环境影响的系统信号部分，本研究采用ARIMA(p,d,q)对其进行仿真计算，将699组训练样本及31组测试样本的系统部分代入模型，对输入时序进行平稳化二阶差分处理，其处理后的差分序列如图9所示。

图9 系统信号的二阶差分序列Fig.9 Second-order difference sequence of system signal

由图9所示，二阶差分序列近似均匀分布在0刻度线上下，基本满足平稳性要求，即差分处理阶数d为2。依据二阶差分序列的ACF图、PACF图以及BIC信息准则确定ARIMA(p,2,q)模型中自回归阶数p和移动平均阶数q，同时也需对模型残差序列同样进行ACF和PACF计算以检验其随机性，其ACF图、PACF图以及BIC信息如表1所示。

表1 BIC信息准则对比Table 1 Comparison of BIC information guidelines

由图10中的(a)和(b)所知，二阶差分序列的ACF和PACF图皆具有拖尾特征，因此确定了建立ARIMA(p,2,q)模型的可行性。经过备选模型的试算对比，最终优先选择BIC值最小、R2值最接近于1、MAPE值最小的ARIMA(1,2,1)模型，即p和q皆为1。观察图10(c)和图10(d)中残差序列的自相关系数和偏自相关系数均在95%的置信区间范围内，说明残差序列为白噪声随机信号，验证了计算模型的有效性和可靠性。同时对31组测试样本进行预报对比，其结果如表2所示。

图10 二阶差分序列及残差序列的ACF和PACF图Fig.10 ACF and PACF diagrams of the second-order difference sequence and residual sequence

由表2可知，基于混凝土坝位移监测时序的系统信号ARIMA(1,2,1)模型的预报效果很好，误差基本上都<0.1，平均误差值为0.029 2。最后，将系统信号模型与细节信号模型计算结果有机叠加，建立了基于多尺度自回归模型体系的混凝土坝位移组合模型。为了验证该组合方案的有效性和优越性，将其拟合预报结果与传统逐步回归模型进行对比，对比情况如图11所示。

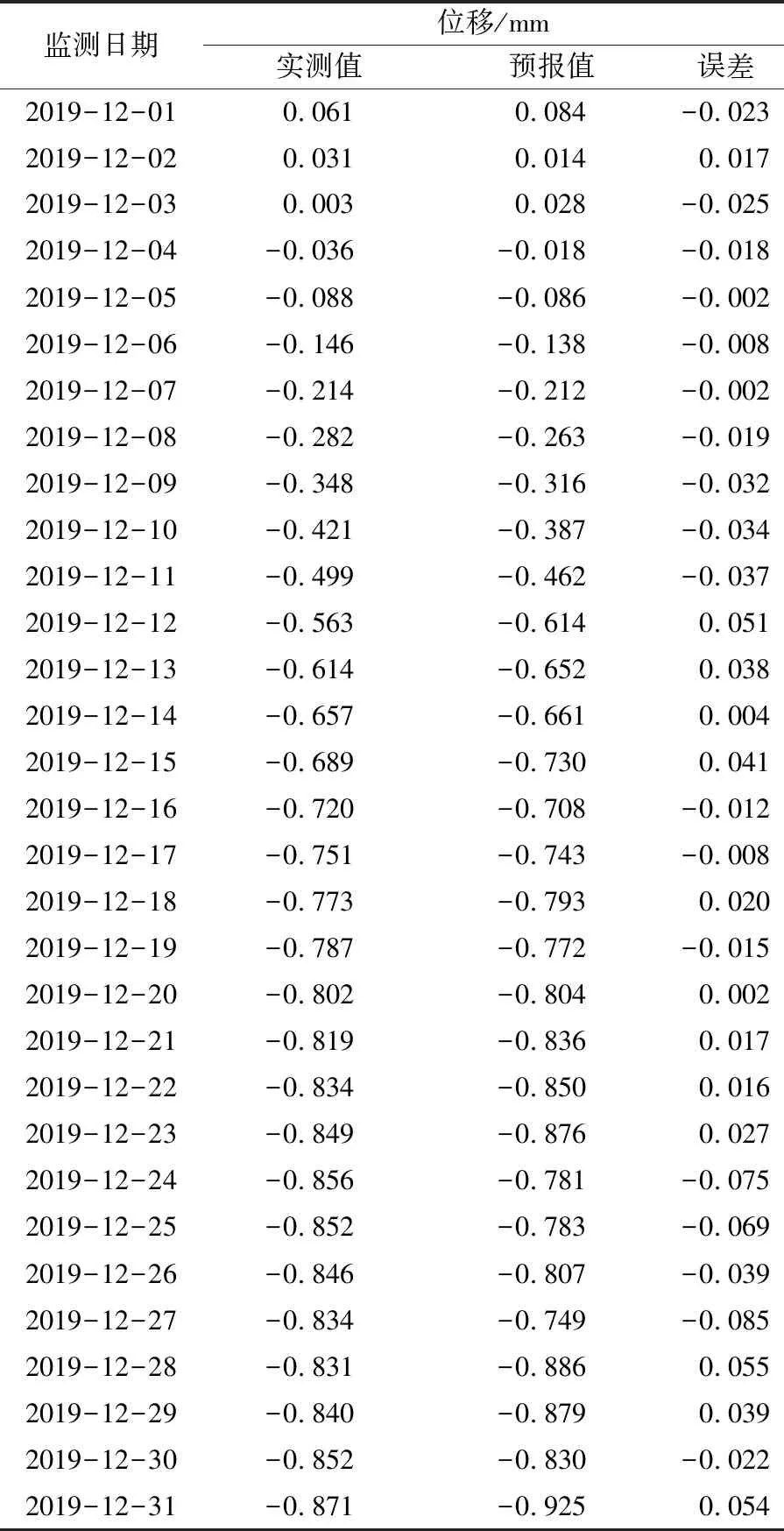
表2 系统信号模型的预报效果Table 2 Forecast effectiveness of system signal model

图11 组合模型与传统模型的计算效果对比Fig.11 Comparison of calculation effectiveness between combinatorial model and traditional model

从图11可知，传统逐步回归模型拟合效果一般，虽大致趋势与实际情况相符一致，但细节部分不能精细化仿真，预报能力有限。组合模型的计算能力出色，对细节处理能力较强，预报精度能满足基本实际需求。为了检验组合模型的泛化能力及排除数据的偶然性，选取该混凝土坝第2号坝段的倒垂线测点IP2水平位移自动化监测时序为研究对象，建模拟合时间为2017年1月1日至2018年12月31日，校模验证时间为2019年1月1日至2019年1月31日，以此可逐一排查空间(测点位置)与时间(监测日期)的偶然性。其计算结果采取统计学领域的评判指标进行衡量，并与PL4测点计算结果统一归纳，详实情况见表3。

表3 各监测点预报模型的统计指标Table 3 Statistical indicators of forecast models at measuring points

综合对比表3中两测点不同时序所建模型的统计指标，可见组合模型的MAE、MSE、MAPE皆远小于传统模型，且R2值更接近于1，表明其模型计算值更接近于实际观测值，以此说明组合模型对于混凝土坝位移监测时序的适用性和可靠性，也验证组合模型相比于传统模型有效提高了预报精度和泛化能力。

5 结 论

(1)考虑到混凝土坝的位移监测时序蕴含多频信号交叉影响且多元环境驱动等工程信息特征，构建了一种基于多尺度自回归模型体系的组合预报模型，有效规避了单一数学模型在进行信号仿真时存在的学习局限。

(2)本文研究了一种混凝土坝位移监测时序的分频组合计算方案，精准发挥了不同数值模型的各自优势，结合NARX模型和ARIMA模型分别对高低频信号进行拟合预报，较好适应了大坝位移监测时序的高度非线性特征，可实现位移效应的精准预报以掌控大坝服役的健康状况。

(3)基于多尺度自回归模型体系的组合建模思路为关于渗流量、裂缝开度和扬压力等其他荷载效应集的水工建筑物安全监控模型的建成计算开拓了新视野，但其预报能力目前只适用于短时工作，如何实现长期预报亟待进一步深入研究。