空间除臭设计风量理论计算方法探究

于文俊 徐婷婷 周燕昭

1 北京市市政工程设计研究总院有限公司

2 北京时代桃源环境科技有限公司

0 引言

垃圾处理厂空间除臭的风量确定的方法有换气次数法[1-2]，数值模拟法[3-4]等。其中，以换气次数法最为常用。

换气次数法是根据以往工程经验结合实际效果定性分析而定，简单易行，但并无确切算法。在垃圾处理过程中，各空间尺寸差异巨大，臭气逸散情况复杂，换气次数法的合理性和准确性值得商榷。

数值模拟方法可以全面反映空间内气流分布情况，能够极大的优化除臭系统设计。但是，数值模拟计算时间长，边界条件复杂，需要结合具体工程建模，缺乏普遍指导意义。

风量作为空间除臭系统设计的关键参数，既关系到空间环境质量是否合格，又影响系统的除臭效率和技术经济性。其简单适用的理论计算方法值得深入的探究。

1 除臭简化模型及浓度函数推导

实际上，在通风过程中，空间内臭气成分的物理和化学特性并未发生变化。通风过程只是一种耦合污染物散发与新风补入双重因素而引发空间污染物浓度变化的过程[5-6]。建立合适的污染物扩散模型，对于工程设计和环境管理具有重要参考意义[7-8]。

为了明确持续通风作用下空间污染物浓度变化规律，假设空间内某种污染物的发生量为QPg/s，密度为ρg/m3；通风量为Lm3/s，其污染物浓度为C0g/m3；空间体积为Vm3，空间内污染物初始浓度为Cig/m3；在通风量L下，通风时间t时的污染物浓度为C。为了简化模型，设定如下假设：

1）空间为广义空间，即包括建筑空间、设备内空间等。

2）QP值由垃圾的物化特性决定，忽略通风对该值的影响，为定值。

3）L，C0为定值。

4）通风开始时间记为t=0。

5）污染物浓度C为时间t的连续函数。

6）通风后空间内空气迅速混合并均匀。

为了探讨污染物浓度C与时间t的关系，取一时间微元Δt，易有：污染物散发量为QPΔt，送风带入的污染物总量为LC0Δt，根据质量守恒原理，可得，排风带走的污染物总量为(L+(QP/ρ))C(ε)Δt。其中，空间内的污染物质量随时间的变化量为QPΔt+LC0Δt-(L+(QP/ρ))C(ε)Δt。空间除臭简化模型如图1。

图1 空间除臭简化模型图

结合污染物浓度的定义，很容易得到，空间内污染物平均浓度随时间的变化量为：

整理上式，即可得到空间内污染物平均浓度随时间的变化率为：

当Δt→0 时，必存在ε→t使上式极限存在，即有：

此式即为污染物浓度变化的基本方程。它是变量可分离的一阶常微分方程，易求其通解为：

此式即为浓度函数，其阐述了在通风作用下空间内污染物浓度随时间的变化关系。很容易看出，浓度函数随时间的增长呈指数变化。这为计算不同时段空间内的污染物平均浓度提供了方便。

式中(L+(QP/ρ))/V项，分子为单位时间排风量，分母为空间体积，显然，此项为单位时间的换气次数。

令，

并整理式（4），得：

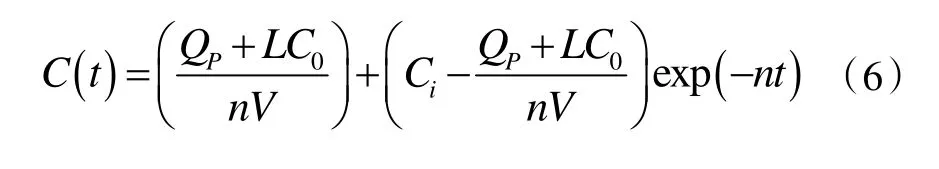
2 浓度函数分析

2.1 污染物体积散发项分析

相比文献[9]中提到的建筑通风行业常用的稀释方程，式（6）与其显著的区别在于增加了QP/ρ项，该项为密度函数中的污染物体积散发项，表征的是单位时间污染物散发的体积。换言之，文献[9]中忽略了污染物散发体积对整体通风体积的影响。

在常规的建筑通风中，污染源少，散发强度小，单位时间内污染物散发体积远小于通风量，其对整体计算的影响可以忽略不计。然而，对于垃圾处理工程而言，情况不尽相同，原因如下：

1）垃圾处理工程中，污染物散发强度大，散发面积广。散发量QP表征的是单位时间整个空间内的污染物的总散发质量。显然，该值与空间内垃圾堆置体积、暴露面积等垃圾总量息息相关。在垃圾坑、堆肥车间等存在大量垃圾堆置的建筑空间内，该值对通风量的影响不容忽视。

2）为了抑制污染物无序散发，垃圾处理工程中的处理设施（设备、传送带等）常采取密闭措施并实施负压控制。为了降低密封系统成本，保证密封的效果以及最大化的设备利用率，密闭处理设施内的通风空间一般较小。并且为了避免补风波动影响系统负压，一般不设置单独的主动补风，主要以缝隙渗透补风为主（卸料、检修工况除外）。基于上述原因，密封设施内的通风量一般较小。尤其地，垃圾处理过程中的振动、翻转、压缩等扰动会强化污染物散发，使污染物散发量明显高于平时。综合考虑上述因素，散发量QP对通风量的影响不可忽略。

另外，QP/ρ项是公式中进出口风量平衡的关键项。平衡方程缺少此项，违背质量守恒原则。

综上所述，考虑密度函数的准确性和普遍适用性，推荐在设计应用时计算此项，尤其是在垃圾污染物重点散发区域和通风空间狭小区域。

2.2 极限分析

对t→+∞时的C(t)函数极限进行求解：

可见，当t→+∞时，空间内的污染物平均浓度有极限浓度C∞。该浓度与时间和空间无关，只与污染物密度，散发量，通风量有关。

式（QP+LC0）/(L+（QP/ρ）)中，分子为空间内单位时间污染物质量增加量，分母为单位时间的排风量。因此，该式可以理解为在持续通风作用下，稳定状态时排风口的污染物浓度。显然，随着时间的增长，空间内污染物平均浓度逐渐趋近于稳定状态下排风口的污染物浓度。

1）特例分析

特别地，式（7）存在下述工况（表1）：

表1 两个特例

其中，工况1 表明，若密闭空间内不存在污染物散发源，无论空间内初始浓度如何，在持续通风作用下，空间内污染物平均浓度将逐渐趋近于新风中的污染物密度C0。该工况适用于检修或卸料完成后（检修门或卸料门关闭，且无其他散发源），在持续通风作用下最终的空间内污染物平均浓度判断；工况2 表明，若密闭空间内存在稳定的污染物散发源且未采取任何通风措施，随着时间的延长，空间内污染物平均浓度将逐渐趋近于污染物密度ρ。该工况适用于长时间无通风作用的密闭空间内污染物平均浓度判断。

2）极限风量

除上述工况外，为分析通风与空间内污染物设计浓度的一般关系，整理式（7）如下：

将L0定义为极限通风量。其意义在于：对于任一个特定的浓度限值，总有一个通风量与其匹配，这为确定设计风量提供了方便。值得注意的是，式（8）应用的前提是t→+∞，换言之，设计风量并不能够直接的取用L0。

2.3 浓度函数增减性分析

虽然设计风量不能直接取用L0，但是分析浓度函数C（t）特点可知，必然存在某一风量可使空间污染物浓度在有限的时间内达到设计浓度C，这一风量即为设计风量L。设计风量的取用范围取决于浓度函数的增减性。

由上，对式（4）求导，可得

令：

显然，C（t）增减性由y的正负决定。

结合设计浓度C、初始浓度Ci和新风中的污染物浓度C0讨论式（4）的增减性如表2：

表2 增减性与风量关系表

正如表1 工况2 所述，空间内仅有该种污染物（全部充满此种气体，无其他气体存在）时，污染物浓度Ci与污染物的密度ρ相等，此时污染物浓度最大。然而，在垃圾处理工程中，空间内存在多种污染物，即空间内的污染物浓度Ci恒小于该污染物的密度ρ，即Ci<ρ。因此表2 第②种工况不存在。

同样，易推出表2 第③种工况中，L<0。其含义是与模型定义方向相反的通风。此种工况称为转移工况，既将臭气由低浓度（Ci）空间转移至高浓度（C0）空间，再由高浓度空间内的除臭系统统一收集处理。类似地，在表2 第⑦种工况中，当时，也可用于转移工况。实际上，本文研究的重点在于设计通风量L>0 时空间浓度的变化情况，因此转移工况不予讨论。

相对地，在表2 第⑦种工况中，只要存在任意L>0，浓度函数均递增。

令

将Li定义为临界风量，其实际意义在于Li是浓度函数C(t)增减性的分界点。显然，Li并不总是大于0，其正负取决于Ci与C0的关系。

综上所述，设计风量L>0 时，具备实际意义的讨论简化为表3 四种工况。

表3 增减性判断准则

显然，浓度函数C(t)在定义域内具有单调性，其增减性与临界风量Li有关。浓度函数C(t)的增减趋势可以表示如图2：

图2 浓度函数C(t)趋势图

显然，通风并不总是具有“稀释”作用（空间污染物浓度随时间增长而减小）。当L

3 设计风量的选取

3.1 风量选取区间

值得注意的是，虽然Li与L0的公式相近，但并不等同。首先，由于C并不总是等于Ci，因此两式并不相等；其次，临界风量决定函数的增减性，而极限风量决定空间污染物浓度能够无限趋近的极限值。

令

容易判断，L是关于C'的递减函数。

利用式（12），根据C和Ci的大小关系，即可判断与其分别对应的L0与Li的关系；结合表3 即可做出设计风量选取区间推断，如表4。

表4 设计风量选取区间

因为L是关于C' 的递减函数，若LC，既当设计选用风量小于极限风量（设计浓度限制C对应的极限风量L0）时，有限的时间内，虽然C'→C+，但总是大于C，而设计期望的是C'≤C。因此表4 中②或④工况不能满足要求。

由上，设计风量选取区间推荐如表5：

表5 设计风量选取区间

特别地，当L→L0-，浓度偏差小于工程许可范围时，表4 中②或④工况仍可酌情采用。

一般而言，满足本节选用规则的设计通风量，均能使空间污染物浓度达到设计要求，区别只在于所需时间不同。

3.2 总换气次数估算

换气次数法简便快捷，工程中应用普遍，通常根据以往工程经验确定。本文尝试从理论出发探讨其估算方法。

结合上文，分析式（12）可知，当L→L0时，C→C∞。若C与C∞的偏差缩小到一定范围，工程上可近似的认为满足要求。

基于此，引入偏差α，令

则有：

假设已知实际浓度C，初始浓度Ci以及允许偏差值α，联立式（4）、（7）、（14）可得：

令N=nt，整理上式得：

其中，N的含义为：空间内平均污染物浓度达到实际浓度C时所需要的总换气次数。从此式可以看出，总换气次数与时间、空间无关，仅与C、Ci和α有关。值得注意的是，总换气次数（次）与设计中常用的单位时间换气次数（次/h）并不相同，其关系为N=nt。另外，α在定义时，并未明确其正负，因此，正负偏差均适用于此式；α的取值范围可以根据各工程实际情况确定。

4 结论

1）浓度函数具有单调性，随时间增长呈指数变化。

2）进行垃圾处理工程除臭计算时，浓度函数中考虑污染物体积散发项QP/ρ是必要的。

3）t→+∞时，空间内污染物平均浓度与时间和空间无关，只与污染物特性，散发量，通风量有关。

4）通风并不总是具有“稀释”作用，当L

5）浓度函数存在极限，其增减性与临界风量有关。

6）结合临界风量和极限风量分析，给出设计风量推荐选用区间及计算流程，并推导了总换气次数的估算公式。