高通量连续流微反应器的流动与传热数值模拟
朱 杰,潘 腾,王丽军,成有为,李 希
浙江大学化学工程与生物工程学院,浙江 杭州 310027
随着连续化、自动化和智能化生产观念的深入,连续流反应技术在精细化工和药物化工领域快速发展[1-2]。作为一种典型的连续流反应器,微反应器凭借自身高效的传热和传质性能在有机合成反应中得到广泛应用[3-4]。然而,微尺度在带来优越的传递性能的同时也限制了流动通量,微反应器的大规模工业应用仍有许多挑战[5-6]。
微反应器的放大策略主要有三种[7]:一是平行数目放大,该方法的优点是可以保持传递性能不变,难点在于如何实现成千上万台设备的流量均布;二是串联数目放大,该方法无须流量分配器,可以应用于较长反应停留时间的反应以及多步反应,但是能够实现的通量有限,鲜有超过100 mL/min处理量的报道;三是几何尺寸放大,该方法可以实现通量的数量级增长,降低通道堵塞风险,难点在于保留微尺度的传递性能。康宁公司基于几何尺寸放大的策略设计了一种先进流反应器(Advanced Flow Reactor,AFR)[8-10],该反应器的特征几何尺寸为宽1 mm、高1.1 mm,流动通量达到10~200 mL/min,气-液相界面积为160~1 300 m-1[11],液-液相界面积为1 000~10 000 m-1[12],仅需七个AFR组合就可实现每分钟公斤级的原料处理量,展现出了一定的工业应用潜力。Fang等[13]自行设计了一种可以连续合成季铵盐的反应器,该反应器由内径为9 mm、总长为200 m的钛材蛇形圆管构成,管内容积为15.7 L,在管内插入组合式静态混合器以增强传热和传质效果,结果表明该反应器可以在几分钟内实现相当于间歇反应器10 h的生产能力,年生产能力超过1 000 t。
本研究基于扩大通道尺寸并内置三维螺旋构件的思路设计了一种高通量连续流反应器(High-throughput Continuous-flow Reactor,HTCR),该反应器在保持较优的混合与传热性能的前提下,通量比常见微反应器增加1~3个数量级,为微反应器的几何放大提供了一条新的思路。本工作首先介绍HTCR的几何构型,再采用计算流体力学(CFD)的方法对反应器基本单元的对流传热过程进行模拟,分析其流动与传热规律,随后采用单因素分析的方法考察雷诺数、普朗特数、螺旋片长径比和扭转角对传热的影响,最后通过数值拟合得到努塞尔数与流动摩擦系数的计算关联式。
1 反应器几何构型设计
流体的旋转、拉伸及剪切,对强化流体传热、混合和传质有重要作用。借鉴SK静态混合器的结构,提出了一种新的连续流反应器型式,其基本单元为内置SK螺旋片的六角直管。如图1所示,六角管横截面为正六边形,SK螺旋片为左旋、右旋交替出现的周期性结构,相邻元件头尾交叉角90°,将六角管与SK螺旋片组合在一起,即构成HTCR的基本单元。

图1 内置SK螺旋片的六角管示意Fig.1 Schematic diagram of hexagonal tube embedded SK helical plates
将基本单元沿六个外壁面法向阵列再切割形成反应管束,如图2所示。将反应管束轴向的两个端面套上固定板,在板上按一定的规则开槽使每根六角管依次连通,连通后的槽口布置如图3所示。将槽口表面封闭后再将z方向两个端面用矩形板封闭,并在第一根六角管上开若干进料口,在最后一根六角管上开一个出料口,此时反应器的流体通道构建完毕,反应器内物料流向如图4所示。

图2 反应管束示意Fig.2 Schematic diagram of reaction tubes bunch
反应管束中六角管外的区域为换热介质区域,在x方向上两个端面分别设置换热介质进、出口,在进口与反应管束间设置分布器,各部件的装配关系如图5所示。

图5 零部件装配Fig.5 Assembly diagram of parts
反应器运行时,反应物分别通过不同的进料口进入第一根六角管,在螺旋片的作用下进行快速混合与高效传热,然后沿立体蛇形路径流至最后一根六角管再从出料口流出。换热介质通过管线进入分布器,从分布器孔流入反应管束壳程,通过间壁传热与管内反应物进行热交换,两流体错流换热。
2 数学模型
2.1 几何模型
抽取流体通道的最小重复单元作为几何模型,如图6所示,l为一个螺片的长度,横截面正六边形边长为5 mm,内置n组螺旋片。

图6 几何模型Fig.6 Geometric model
2.2 控制方程
对于不可压缩牛顿流体的三维稳态流动,忽略质量力,以张量形式表示的控制方程如下:
连续性方程

动量方程
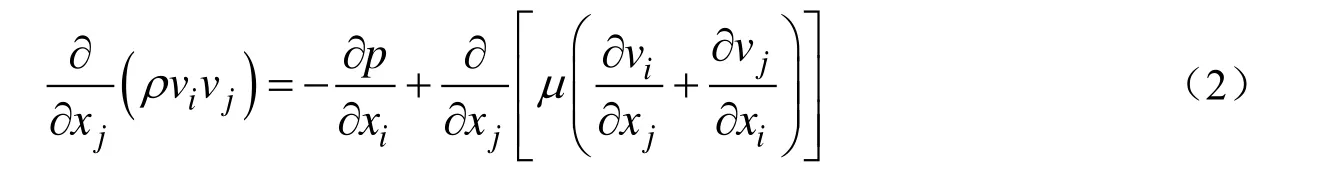
能量方程

由于模拟的雷诺数(Re)在湍流区(对于SK螺旋结构,Re>150即为湍流区[14])。根据以往对于三维剪切流的研究,剪切应力传输模型(SST)k-ω湍流模型可以更准确地描述流体行为[15],故本研究选用该模型进行计算。
2.3 网格划分及无关性分析
采用软件Star ccm+的网格划分功能,贴近壁面设置5层棱柱层网格以解析边界层,保证算例中壁面y+值为0.1~1.2,网格划分情况如图7所示。
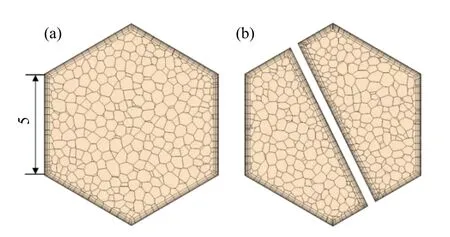
图7 网格划分进口段(a)和SK段(b)Fig.7 Mesh of inlet section(a) and SK structure section(b)
网格无关性分析的边界条件设置:进口速度为0.3 m/s,进口温度为60 ℃;出口为压力边界,其值为0 Pa;几何壁面为无滑移边界条件,外壁面温度设为等温80 ℃,螺旋片壁面设置为绝热,流动介质设置为水。由疏到密选取了163 659,262 874,418102,566 706,866 350和14 490 616六个网格总数目进行计算,以模拟对象的努塞尔数(Nu)和摩擦系数(f)作为判断依据,结果如图8所示。结果显示,f在整个考察范围内均保持稳定,当网格数大于56.6万时,Nu几乎不随网格数的增长而变化,此时网格尺寸已经可以消除其本身对计算结果的影响,本文案例均采用该尺寸进行计算。

图8 网格无关性分析Fig.8 Grid independence analysis
为了排除进出口对计算结果的干扰,进一步考察螺旋片组数(n)对流动和传热的影响,模拟结果如图9所示。当n≥6时,Nu和f趋于平缓,说明此时螺旋片组数对于传热和流动阻力已经几乎没有影响,故本模拟计算的n均以6为基准。
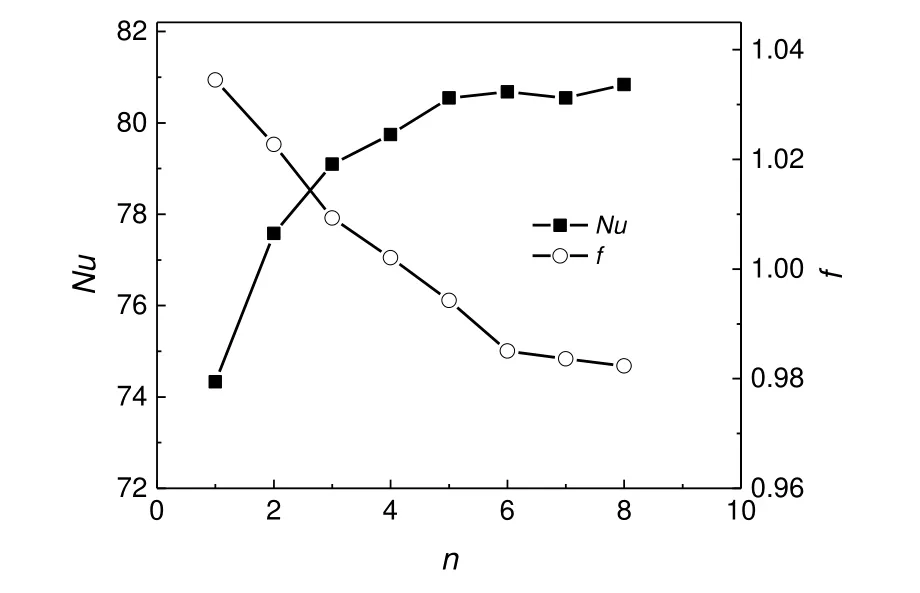
图9 螺旋片组数对Nu和f的影响Fig.9 Influence of group number of spiral pieces on Nu and f
3 结果与讨论
3.1 速度场与二次流
图10展示了模拟对象的流线图。可以看出流体在管内呈现出不断分裂合并的流动状况,与此同时,流体在径向上还有大量的穿插和交互,这些径向上的二次流对于强化传热具有重要意义。
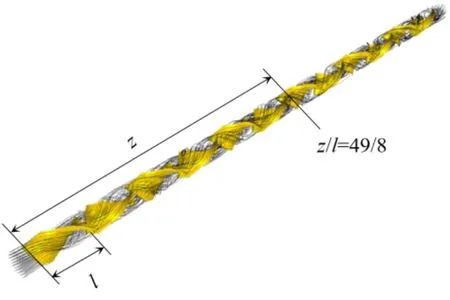
图10 模拟对象的流线Fig.10 Streamline of simulation object
为了细致分析流体在径向上的流动,考察了第七个螺旋片对应区域的横截面速度场的变化情况,结果如图11所示。z为模型横截面距入口的长度,则z/l可便捷地表示横截面所处位置,比如z/l为49/8就代表第七个螺旋片轴向1/8长度位置的横截面,黑色箭头矢量表示速度在横截面上的投影;颜色等值线表示轴向速度大小。

图11 第七个螺旋片不同横截面的速度场Fig.11 Velocity field of different cross sections of the 7th helical plate
可以发现每个截面上都存在径向二次流,这是因为流体在螺旋前进的过程中,轴心附近的流速高于管壁附近的流速,不同流速的流体微团的离心力不同,径向上产生了逆压梯度,引起流体从轴心向螺旋外侧管壁的流动,同时还会引起流体沿管壁从螺旋外侧向内侧的附加流动,形成一对反向的双旋流涡,这对旋涡又被称为Dean涡[16]。图11中螺旋片两侧各有一对Dean涡,图11(a)和图11(b)中每一对都是两个同向涡组成,这是因为相邻的两个螺旋片头尾呈90°交叉布置,第六个螺旋片产生的两对Dean涡进入第七个螺旋片时,四个涡被重组,旋向相同的两个涡进入了第七个螺旋片的同一侧。由于同向的两个涡的动能会相互抵消,可以观察到:从图11(a)到图11(b),涡的强度在逐渐变弱;图11(c)时,其中一个涡消失;图11(d)时,涡消失的区域形成了一个与消失前反向的涡;再从图11(e)到图11(h),两对反向涡不断发展、平衡,如此再进入第八个螺旋片。整个流体区域的二次流都表现出这种周期往复的特性。
3.2 温度场及传热过程强化
在二次流的影响下,反应器的传热过程也得到了强化,图12所示为第七个螺旋片不同横截面的温度场情况。颜色等值线表示温度场,线状的纹理表示速度矢量在横截面投影的线积分卷积。
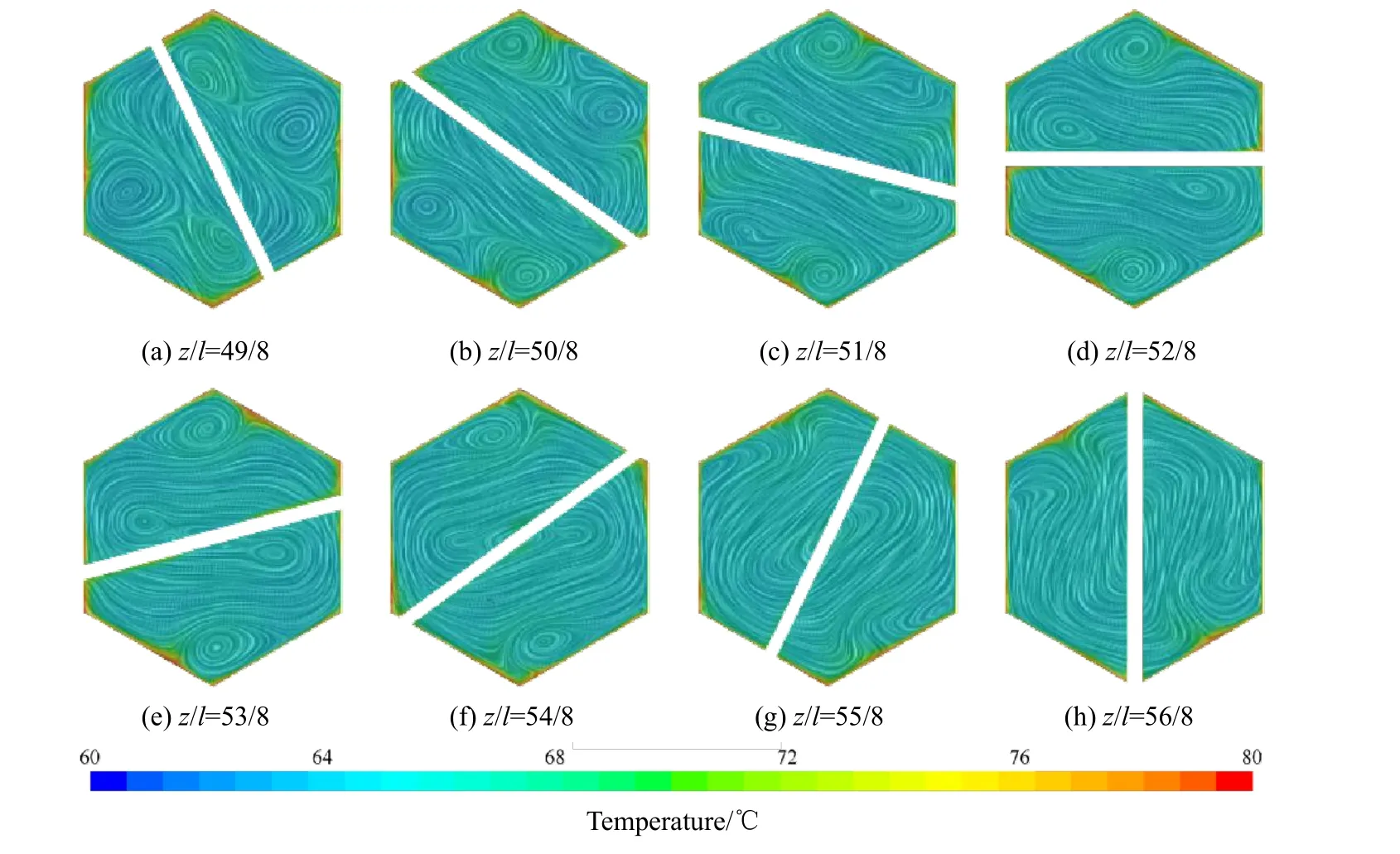
图12 第七个螺旋片不同横截面的温度场Fig.12 Temperature field of different cross sections of the 7th helical plate
由图12可知,热边界层很薄,整个横截面的绝大部分区域温度是均一的,这是由于在二次流的作用下,流动主体区的冷流体不断侵扰边界层的热流体,边界层的热流体不断被卷入流动主体区的冷流体,这个过程中不仅流体微团的位置发生了交错,流体微团的温度也在快速交换和平衡,形成了大面积温度均一的区域。
为了更加直观地展现SK螺旋结构强化传热的能力,以相同边界条件下无构件空管的温度场为对照,三个截面的中轴线温度分布如图13所示,横坐标χ为横截面径向上的无量纲长度。可以看出随着轴向距离的增大,SK结构对应的主流区温度快速上升并逐渐趋于均一,而空管对应的主流区温度仅缓慢上升,并且径向分布很不均匀。在该条件下,SK螺旋结构的传热系数为空管的4.2倍。

图13 不同横截面中轴线的温度分布Fig.13 Temperature distribution of the central axis with different cross sections
3.3 场协同效应分析
将对流传热比作有热源的热传导,传热速率不仅与流体物性和流速有关,还与速度场与温度梯度的夹角有关。当流体被加热时,应使夹角尽量接近0°,当流体被冷却时应使夹角接近180°,这一思想被称为“场协同原理”[17-18]。

通过式(4)计算不同截面的协同角,结果如图14所示。可以看出有较大面积区域的协同角偏离90°,这说明SK螺旋结构产生的二次流对于强化传热起着重要的作用。观察图14(a)~图14(c)红色与蓝色区域的演变,可以发现绿色区域占比逐渐增多,这表明流过第六个螺旋片的流体二次流在第七个螺旋片的反旋向导流下逐渐减弱。在第七个螺旋片的后半段,即图14(d)~图14(h)所示的截面位置,图中红蓝色区域的占比明显增多,这是由于流体在第七个螺旋片的主导下逐渐形成新的Dean涡,二次流再次发展增强。

图14 不同截面的协同角分布Fig.14 Synergy angle distribution of different cross sections
3.4 雷诺数与普朗特数对传热的影响
雷诺数(Re)和普朗特数(Pr)是影响对流传热的重要因素,通过单因素分析的方式考察了两者对传热过程的影响。为了综合考虑传热与流动阻力两方面的结果,引入性能评价指标(PEC)来量化等泵功约束条件下强化传热的程度[19],计算方法见式(5)。

选取等水力学直径的中空圆管作为参照结构,不同Re时的Nu和f值如图15所示,对PEC的影响如图16所示。可以看出,在其他因素保持不变时,Nu随着Re的增大而增大,f随着Re的增大而减小,PEC呈现先增大再减小的规律。在考察范围内,PEC数值始终大于1,说明SK螺旋结构实现了强化传热。
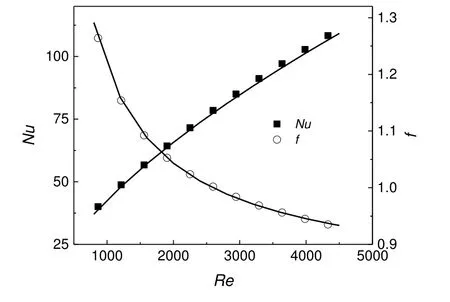
图15 Re对Nu和f的影响Fig.15 The effect of Re on Nu and f
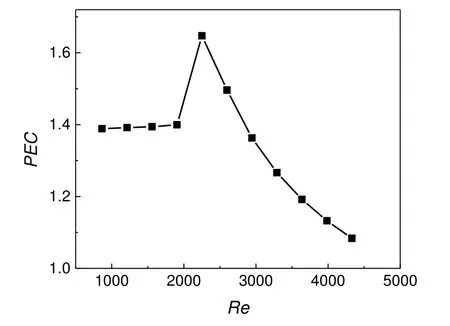
图16 Re对PEC的影响Fig.16 The effect of Re on PEC
通过拟合得到:

Pr对Nu和f的影响如图17所示。可以看到,Nu随Pr的增大而增大,f数值上与Pr无关。拟合得到Nu与Pr的关系见式(8),Pr项指数为0.406,与空管在完全湍流区的Nu实验关联式的Pr项指数0.4基本一致。

图17 Pr对Nu和f的影响Fig.17 The effect of Pr on Nu and f

3.5 螺旋片长径比与扭转角对传热的影响
几何结构也是影响传热过程的因素之一,对于SK螺旋结构,特征几何参数为螺旋片长径比(Ar)和扭转角(φ)。不同Ar对Nu和f的影响如图18所示,对PEC的影响如图19所示。

图18 Ar对Nu和f的影响Fig.18 The effect of Ar on Nu and f

图19 Ar对PEC的影响Fig.19 The effect of Ar on PEC
随着Ar的增大,Nu和f都呈现减小的趋势,这是由于Ar增大会使得单位轴向长度螺旋片旋转角度的下降,二次流的强度减弱。PEC则随着Ar的增大缓慢减小,当Ar>2.4时减小速度变快,因此在实际应用中Ar设计值为1.7~2.4较合适。通过拟合得到如下的关联式:

不同φ对Nu和f的影响如图20所示,对PEC的影响如图21所示,其中φ0为180°。可以看出Nu和f随着φ/φ0的增大而增大,PEC随φ/φ0的增大而显著增大,这说明增大扭转角是一种强化SK螺旋结构传热的理想方式,在实际应用中选择180°扭转角的螺旋片是合适的。
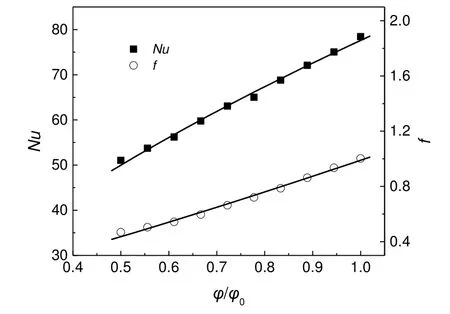
图20 φ对Nu和f的影响Fig.20 The effect of φ on Nu and f

图21 φ对PEC的影响Fig.21 The effect of φ on PEC
拟合得到Nu和f与无因次扭转角的关系式分别为:

3.6 计算关联式
取3.4和3.5的所有数据进行拟合,得到SK螺旋结构的Nu及f的总计算关联式:
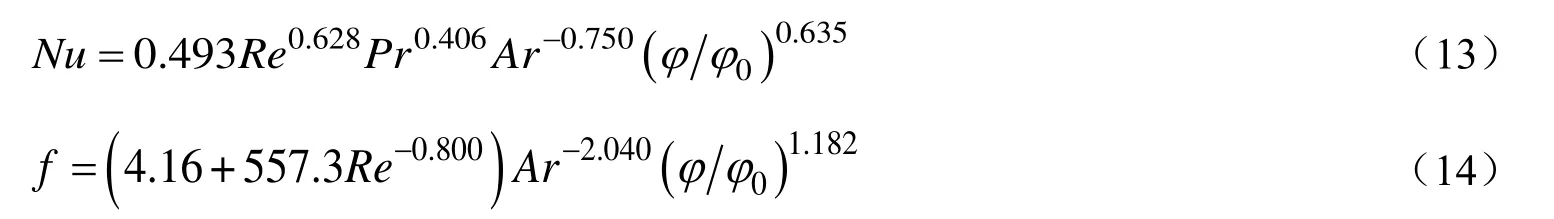
式中:866<Re<4 330,1<Pr<214,1.7<Ar<2.9,0.5<φ/φ0<1。
图22和图23为总关联式计算得到的值与模拟值的比较。

图22 Nu计算值与拟合值的对比Fig.22 Comparison of calculated Nu and fitted Nu

图23 f计算值与拟合值的对比Fig.23 Comparison of calculated f and fitted f
由图22和图23可知,计算值和拟合值的最大偏差都在10%以内。Nu计算关联式的相关系数R2为0.998 1,显著性检验中F值为23 089,F0.95=4.07,F10F0.95;f计算关联式的相关系数为0.999 7,显著性检验中F值为111 353,F0.95为4.16,F10F0.95。两个关联式都有着较好的符合性和预测性。
4 结 论
a)基于扩大通道尺寸并内置三维螺旋内构件的思路设计了一种高通量连续流反应器,通量可达1000 mL/min,比传统连续流微反应器高1~2个数量级;
b)在周期性螺旋片的作用下,流动径向上产生大量二次流,这些漩涡显著了强化传热过程;
c)热边界层很薄,径向上温度近乎均一,SK结构的传热系数为空管的4.2倍;
d)雷诺数(Re)对性能评价指标PEC影响较大,合适的Re为2 000~3 000;
e)螺旋片长径比(Ar)和扭转角(φ)对PEC影响较大,合适的Ar为1.7~2.4,φ为180°;
f)反应器内努塞尔数(Nu)和摩擦系数(f)计算关联式如下:

式中:866<Re<4 330,1<Pr<214,1.7<Ar<2.9,0.5<φ/φ0<1。
符号说明
Ar—— 螺旋片长径比vi—— 速度张量,m/s
cp—— 流体比热容,J/(kg·K)z—— 模型横截面距入口的长度,mm
f—— 流动摩擦系数θ—— 协同角,°
l—— 螺片的长度,mmλ—— 流体热导率,W/(m·K)
Nu—— 努塞尔数μ—— 流体黏度,Pa·s
Pr—— 普朗特数ρ—— 流体密度,kg/m3
Re—— 雷诺数φ—— 扭转角,°
T—— 流体温度,Kχ—— 横截面径向上的无量纲长度

