基于锚节点分布特性的跳距修正的DV-HOP定位算法∗
李跃飞
(湖南信息学院计算机科学与工程学院,湖南 长沙410014)
随着电子技术的发展,无线传感网络(Wireless Sensor Networks,WSNs)已在康复医疗、工业监测等领域广泛使用。WSNs中的节点先感测环境数据,再将数据传输汇聚节点,进而实现对环境的监测目的。具有准确位置信息的感测数据才具有意义。因此,定位成为WSNs领域的一个研究热点之一[1-2]。
尽管全球定位系统(Global Position System,GPS)[3]定位技术很成熟,但是将WSNs中所有传感节点配备GPS,成本太高,而且节点运行GPS增加了节点的能量消耗。对于微型的、能量有限的节点而言,高的能量消耗是无法接受的。
因此,通常在网络内只允许部分节点配置GPS,使这些节点能够获取自己的位置,常将它们称为参考节点或锚节点。现存的定位算法可分为测距定位和非测距定位算法。如基于接收信号强度指标(Receiver Signal Strength Indicator,RSSI)、到达角度和到达时间差(Time Difference of Arrival,TDOA)[4]属基于测距定位算法。相比于非测距定位算法,测距定位算法需一些硬件设备,增加了定位算法的成本以及开销。
据此,非测距定位算法,如质心定位[5]、DVHOP[6]在WSNs中广泛应用。这些非测距定位算法利用跳数等连通信息估计节点位置。目前,研究人员对非测距定位算法进行了深入研究,并得到较满意的定位精度[7-8]。然而,这些算法是基于同构的节点网络。在实际环境场景中,节点间的通信区域是不规则的,并且受障碍物影响,容易形成异构网络,这就影响了定位性能。此外,随机部署节点无法保证锚节点在网络内的分布的均匀性。这直接影响节点的定位精度。
为此,本文考虑到实际环境,正视锚节点分布的均匀性问题,提出对跳距修正的DV-HOP定位算法HDCD。HDCD算法利用全局锚节点信息以及局部信息对跳距进行修正,减少测距误差。在不同拓扑结构下分析HDCD算法的定位性能。性能分析表明,提出的HDCD算法提高了定位精度,增强了对锚节点分布不均匀的恶劣环境的强健性。
1 系统模型
N个传感节点随机分布于二维(2-D)网络区域ℓ×ℓ,如图1所示,其中锚节点占比为p%,未知节点占比为(100-p)%。令αi表示第i个锚节点,其位置坐标为;令sj表示第j个未知节点,其位置坐标为(xj,yj)。
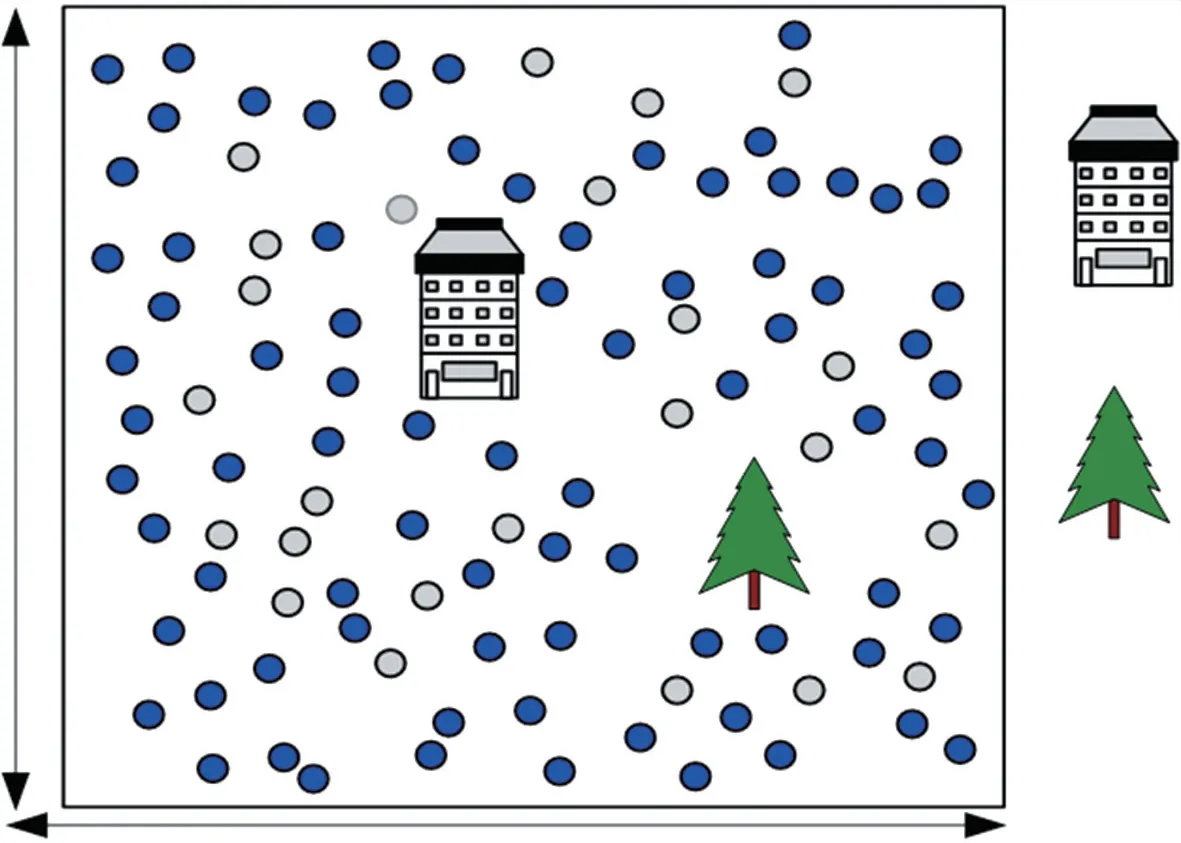
图1 网络模型
假定所有节点具有相同的通信半径Rt。每个节点在其通信范围内能够与它的邻居节点进行直接通信。锚节点利用GPS获取其自身的位置。
与传统的定位算法不同,本文假定区域内存在障碍物,如建筑物、树。这些障碍物影响节点间信号的传输,增加跳距估计的误差。此外,考虑锚节点分布不均匀性对定位精度的影响。本文针对上述问题,对平均跳距进行修正,进而提高定位精度。
2 HDCD定位算法
传统的DV-HOP算法并没有考虑到锚节点分布是否均匀问题。然而,在实际环境中,锚节点分布是不均匀的。换而言之,传统的DV-HOP算法严重依赖于锚节点的分布。针对此问题,HDCD算法对未知节点与锚节点间的距离进行修正。
2.1 锚节点的全局跳距修正
首先,依据传统DV-HOP算法[9]的策略,计算未知节点与锚节点间的最小跳数。具体过程如图2所示。锚节点广播beacon包,其包含其位置以及该beacon包被传输的跳数Nh,最初Nh=0。
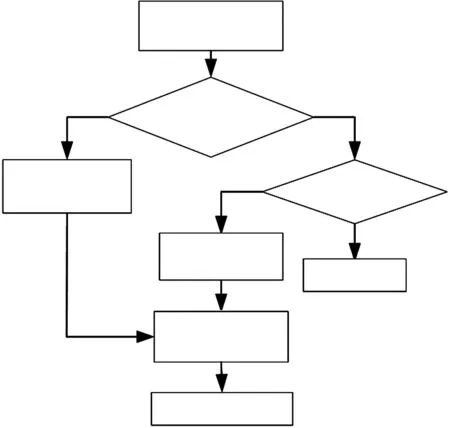
图2 beacon包的处理流程
一旦收到beacon包,节点就判断是否之前已接收过此包。若是第一次接收,就从beacon包中提取发送节点的位置以及跳数信息。并更新beacon包中跳数值(Nh+1),再转播。若之前已接收过此beacon,就将目前所接收的beacon包跳数值与之前存储的跳数值进行比较,并且保存两者中的最小值。
然后,锚节点就依据式(1)计算平均跳距:
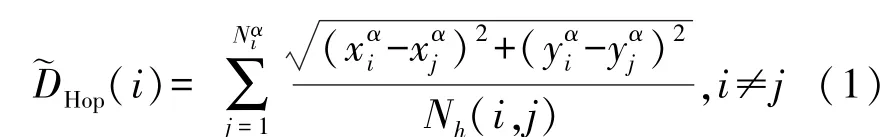
传统的DV-HOP算法是利用式(1)计算锚节点的平均跳距。这存在较大误差,其并没有充分利用锚节点的已知信息计算平均跳距的误差。为此,HDCD算法利用锚节点的已知信息,计算式(1)所计算的平均跳距的误差。式中:εi表示锚节点αi端所计算的平均跳距的误差。

因此,利用该误差εi对(i)进行修正,如式(3)所示:
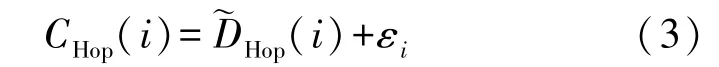
2.2 锚节点的局部跳距修正
由于节点是随机分布于监测区域,网络拓扑结构的不规则概率较大。因此,仅从全局拓扑结构修正跳距是不准确的。为此,HDCD算法也从局部拓扑结构对跳距进行修正。
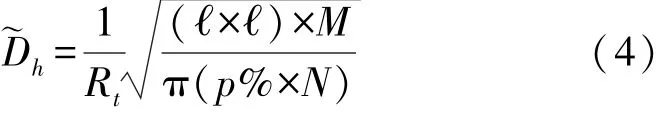
式中:M表示估计一个未知节点位置至少需要的锚节点数;m=p%×N表示网络内的锚节点数;ℓ×ℓ表示监测的区域面积。
锚节点将其获取的离其他锚节点的跳数值进行比较,计算在小于跳数范围内的单跳平均跳距。
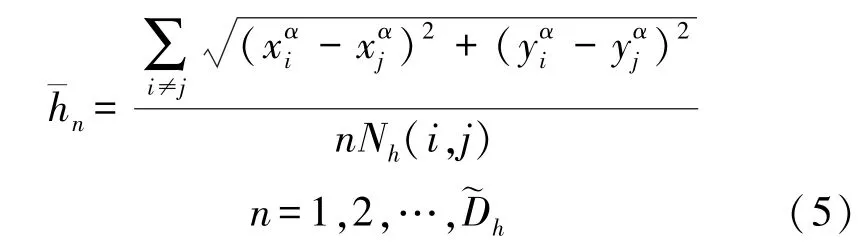
不失一般性,平均每跳的误差服从高斯分布。利用参数估计理论,通过估计误差建立代价函数,再依据最小均方误差准则获取平均跳距[11]。具体过程如下。
构建代价函数,如式(6)所示:

2.3 未知节点离锚节点的距离估计
在真实环境中,两节点间的真实距离与其估计的距离差值并不相同。有些差值小,有些差值大。而依据式(1)可知,平均跳距与两节点间的欧式距离成正比,与它们间中跳数成反比。
如图3所示,图3中有两个锚节点(αr、αq)。利用它们间的欧式距离以及它们间的跳数值计算平均跳距。通常,所估计的距离总是小于它们间的真实距离,如图3(a)所示。在这种情况下,通过修正它们的平均跳距,降低定位误差,提高定位精度。
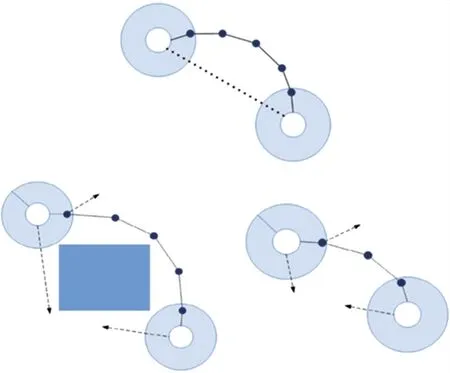
图3 三类情况分析
当存在障碍物时,锚节点间的跳数越大,且所估计的它们间距离小于它们真实的距离,如图3(b)所示。在这种情况下,它们的平均跳距偏小,也需要对它们的平均跳进行修正。
第三种情况:当锚节点间跳数较少,所估计的距离与实际距离偏差较小。如图3(c)所示。在这种情况下,平均跳距对定位精度影响偏小。
依据上述分析的三种情况可知,并结合2.1节和2.2节,未知节点利用式(8)估计距离:
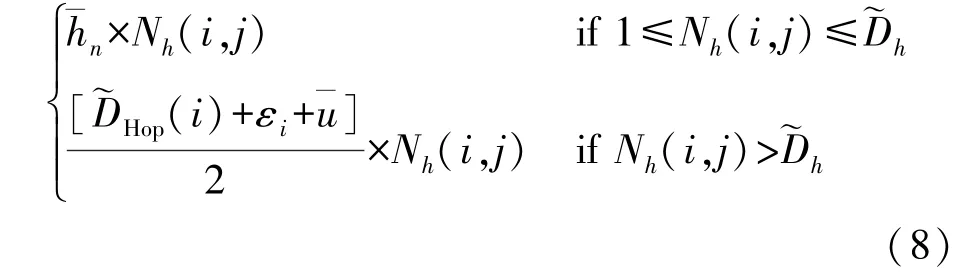
2.4 基于最小二乘法的位置估计
未知节点利用式(8)获取离锚节点间的距离,即测距。假定未知节点sj获取了离κ个锚节点的距离,令αj,1,αj,2,…,αj,k,…αj,κ表示这些锚节点。未知节点sj所测量的离这个κ个锚节点的距离分别表示为
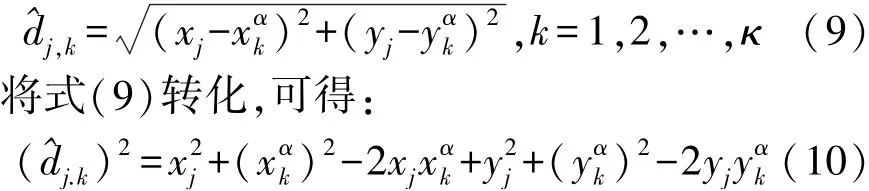
有κ个锚节点就能构建κ个等式。参照式(10),第κ个等式为:

3 性能分析
利用MATLAB R2016a软件建立仿真平台,分析HDCD算法的性能。由于本文旨在分析锚节点的分布均匀性对定位精度的影响,建立四个不同拓扑结构的网络,它们的各项参数值如表1所示。

表1 四种网络拓扑结构的参数值
选用通信半径归一化后的平均定位误差作为性能指标,其定义如式(18)所示:

此外,选择同类的DV-HOP定位算法为参照,对比分析在四种不同拓扑结构下它们的定位误差性能。考虑到随机误差,每种拓扑结构下,独立重复100次,取平均值作为最终的仿真数据。
3.1 Scene-one环境下的定位性能
图4给出Scene-one环境下的拓扑结构示例,其中未知节点数为100,锚节点数为8,锚节点分布均匀。从图4可知,8个锚节点较均匀地分布在监测区域内。
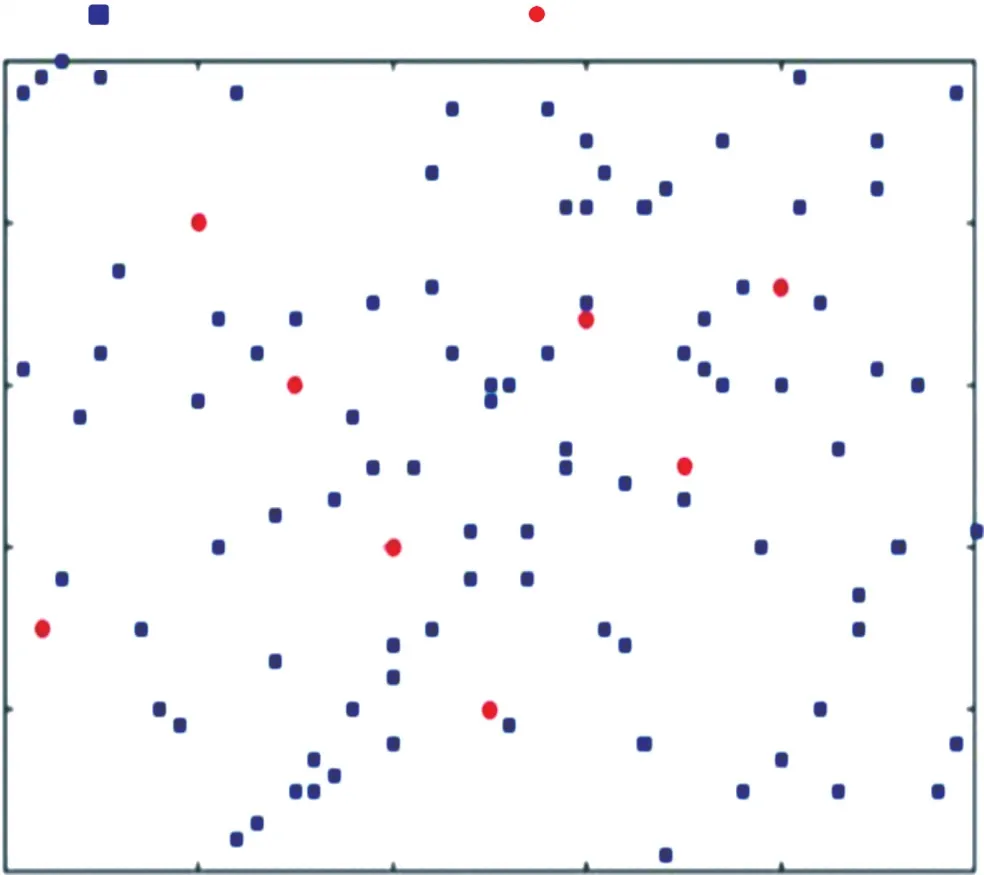
图4 Scene-one的网络拓扑示例(8个锚节点)
图5 给出DV-HOP算法和HDCD算法在Sceneone环境下归一化定位误差。从图可知,相比于DVHOP算法,提出的HDCD算法降低了定位误差。此外,锚节点比例的增加,有利于定位误差的下降。但是定位误差与锚节点数并非呈线性关系。
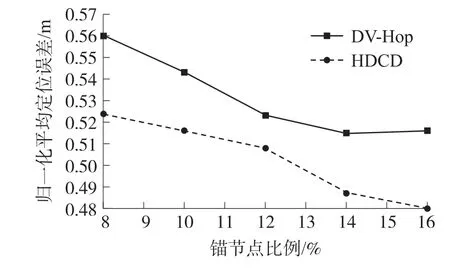
图5 归一化平均定位误差(Scene-one)
3.2 Scene-one环境下的定位性能
图6 给出Scene-two的网络拓扑结构示例,其中未知节点数为100,锚节点数为10,锚节点分布不均匀。从图可知,相比于图5的Scene-one,网络Scene-two中锚节点分布集中,未能在监测区域内均匀分布。
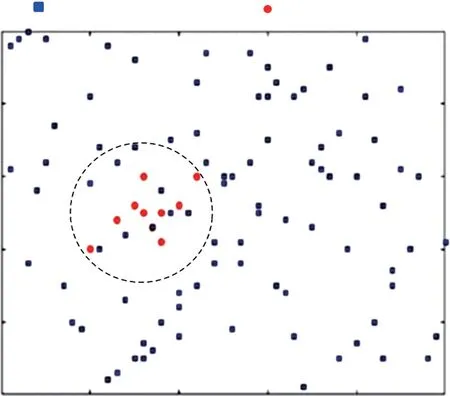
图6 Scene-two的网络拓扑结构示例(10个锚节点)
图7给出Scene-two网络环境下HDCD算法和DV-HOP算法的定位误差随锚节点数的变化情况。从图可知,锚节点数的增加降低定位误差。原因在于:锚节点数的增加,使未知节点获取的测距信息越多,测距误差越低。
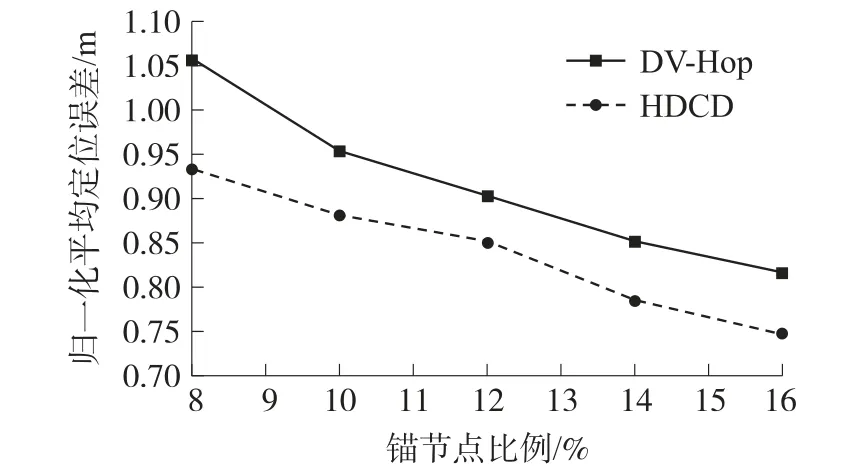
图7 归一化平均定位误差(Scene-two)
此外,相比于Scene-one条件,Scene-two条件下的定位误差偏大。原因在于:锚节点分布不均匀。离锚节点远的未知节点,测距误差较大,不不利于定位,导致定位精度下降。
3.3 Scene-three环境下的定位性能
图8给出Scene-three的网络拓扑结构示例,其中未知节点数为100,锚节点数为10。监测区域内有障碍物,阻碍节点间直接通信。而在远离障碍物的区域锚节点分布较均匀。
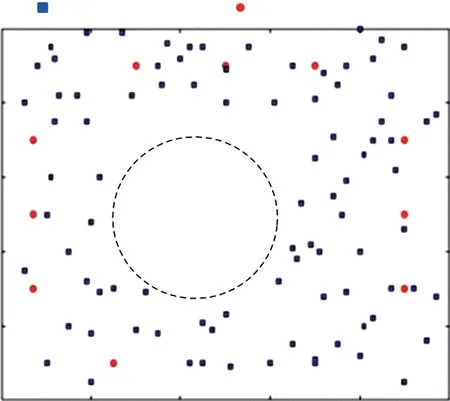
图8 Scene-three的示例(10个锚节点)
图9 给出Scene-three网络环境下HDCD算法和DV-HOP算法的定位误差。从图可知,锚节点数量的增加,使定位误差下降。这符合预期。此外,对比看图8与图7不难发现,Scene-three环境下的定位精度高于Scene-two环境下的定位精度。原因在于:尽管Scene-three存在障碍物,除障碍物所在区域外的其他区域,锚节点分布均匀。

图9 归一化平均定位误差(Scene-three)
3.4 Scene-four环境下的定位性能
图10 给出Scene-four的拓扑结构示例,其中未知节点数为100,锚节点数为14。监测区域内有障碍物,阻碍节点间直接通信。而在远离障碍物的区域锚节点分布不均匀。
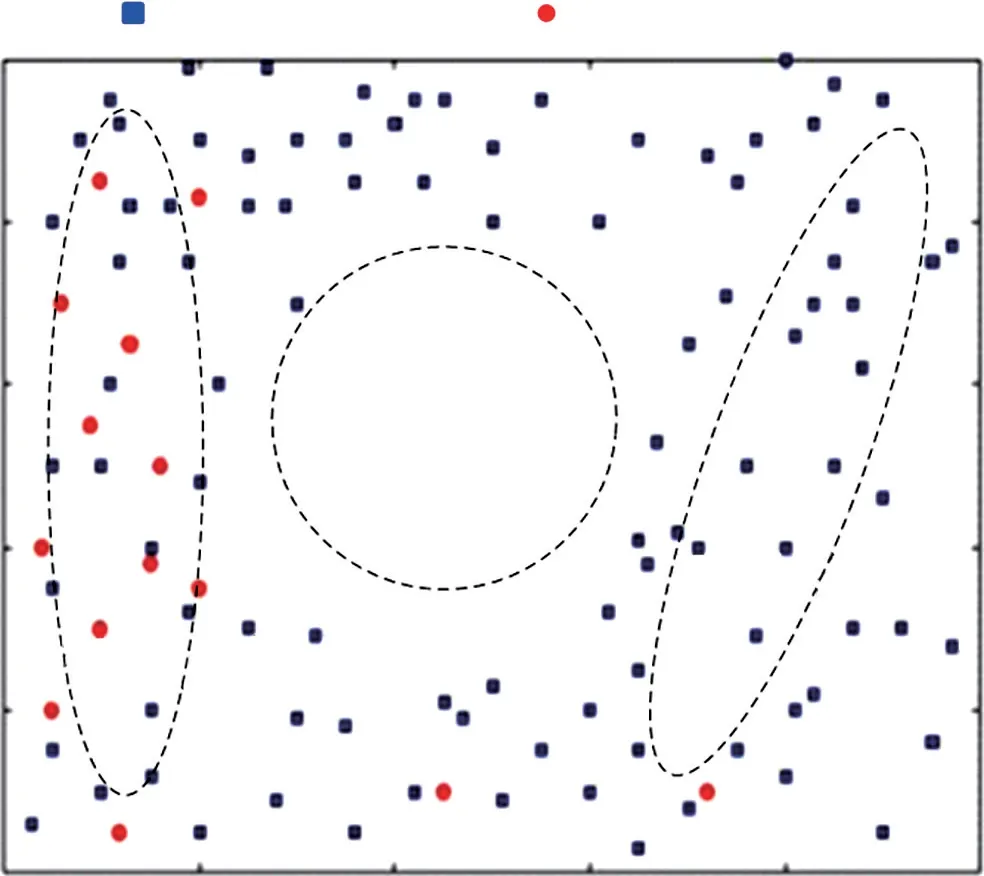
图10 Scene-four的示例(14个锚节点)
图11 给出Scene-four的网络环境下HDCD算法和DV-HOP算法的定位误差。从图可知,锚节点数量的增加,使定位误差下降。这符合预期。此外,对比看图10与图11不难发现,Scene-three环境下的定位精度高于Scene-four环境下的定位精度。原因在于:Scene-four的定位环境很恶劣:既存在障碍物,锚节点分布又不均匀。

图11 归一化平均定位误差(Scene-four)
表2给出四个网络拓扑环境下的定位误差。从2可知,Scene-two和Scene-four两种环境下的定位误差低于Scene-one和Scene-three。这主要因为:Scene-one环境下锚节点分布均匀,又不存在障碍物。尽管Scene-three环境中存在障碍物,但是其锚节点分布是均匀的,并且其通信半径为20 m。节点通信半径的提高,有利于降低定位误差。
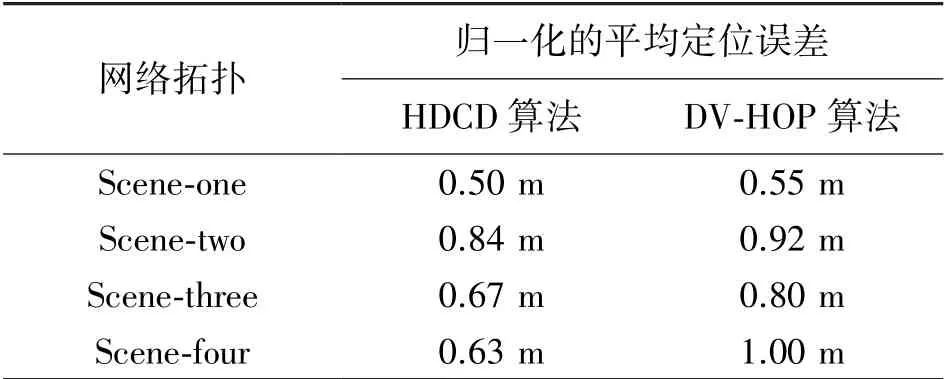
表2 四个网络拓扑环境下的定位误差
4 总结
考虑到实际环境中锚节点分布的不均匀性对定位精度的影响,提出了跳距修正的DV-HOP定位算法HDCD。HDCD算法依据锚节点的分布特性对跳距进行修正,减少定位误差。针对不同拓扑环境,分析了HDCD算法的定位性能。仿真结果表明,相比于DVHOP算法,HDCD算法在Scene-one、Scene-two、Scenethree和Scene-four网络条件下的归一化的平均定位误差分别下降了约9%、6.5%、16%和37%。

