涡街流量计的压电探头最优距离和新型测量方法研究∗

胡 捷黎 波∗肖志锋

(1.江西农业大学工学院，江西 南昌330045；2.江西省畜牧设施技术开发工程研究中心，江西 南昌330045)

涡激振动(VIV)是一种典型的流致振动(FIV)。结构的非流线型会导致其在流体的作用力下产生周期性旋涡脱落，使结构受到与流向垂直的周期性气动力，进而激发结构的横向振动[1]。由于流体流速与旋涡脱落频率有对应关系，因此常制作成多种空气流速传感器，例如，基于上述涡街振动原理研制的涡街流量计，工业级的涡街流量计主要易受环境噪声的干扰，导致其对低速不敏感。同时，空气流速传感器广泛应用于畜禽舍环境控制，风能采集，流量检测，气象监控，等领域[2－4]。例如，在畜禽环境监测领域，通风时流速太快引起畜禽强烈的应激反应或因局部温度骤降导致畜禽强感冒，或造成畜禽的生产性能、免疫能力、生长速度等下降[5－6]，因此，对畜禽舍通风装置的流速检测尤其重要。传统FIV传感器多采用机械转动结构，其结构复杂，对加工精度和机械稳定性都有较高的要求[7]。而近年来利用压电材料作传感元件研制的FIV传感器，其不需要转动部件，且可与微机电系统(MEMS)集成，因此易于微型化[8－10]。

目前，VIV传感器主要采用两种压电材料作为传感元件:锆钛酸铅压电陶瓷(PZT)和聚偏二氟乙烯(PVDF)。PVDF薄膜由于其高柔性的特点，适用于交变载荷的感知[11－12]。然而，压电式流涡激振动(PVIV)流速传感器还有许多不完善的地方。特别是检测低流场流速时(流速低于2 m/s)，涡街压电信号微弱，同时测量现场的噪声干扰相对较强，造成涡街特征信号提取的困难。比如测量过程中，压电元件自身受流场扰动产生的信号、风洞系统产生的噪声信号等，会把涡街特征信号淹没。针对这一问题，许多学者对PVIV流速传感器展开了全面的研究，如绕流体的形状和排布[13－14]、电路检测方式[15－16]以及信号提取方法[17－19]，提高了空气流速测量精度和范围。

PVIV流速传感器的结构采用圆形或梯形旋涡绕流体和PZT或PVDF薄膜为传感元件组成。研究发现，改变绕流体直径会导致绕流与传感器元件之间的距离不同。这表明，漩涡测量位置和绕流体直径将影响PVIV检测精度。针对上述问题，笔者提出了一种基于PVIV流速传感装置。该装置由圆柱绕流体和PVDF压电悬臂梁组成。利用数值模拟方法研究涡街流场特性，分析传感器结构参数对涡街响应信号检测的影响规律。采用通过提取频域曲线中涡激频率下的功率作为涡街的传感强度，增强了感知微弱的流速响应信号，且能够解决噪声等电路上的干扰影响，扩大了对低流速的检测能力。为高灵敏，快响应的空气流速传感器件的设计及测量提供新的探测方法。

1 压电涡激振动流速传感装置

1.1 传感结构

本文PVIV流速传感装置的结构如图1所示。该结构由圆柱绕流体和PVDF压电悬臂梁构成，其中悬臂梁由表面涂有银电极层的PVDF薄膜组成；同时，靠近圆柱绕流体一侧的PVDF压电悬臂梁端部固支。圆柱绕流体直径D＝7 mm，圆柱体中心距PVDF压电悬臂梁固支端距离为L，入射流速为v，其方向垂直于圆柱体表面。仿真计算时，D值的范围为30 mm~70 mm，v值范围为0.3 m/s~2.5 m/s，L值的范围为50 mm~170 mm。为了简化计算和控制多余变量，PVDF压电悬臂梁高度h设定为30 mm。当外界来流作用时，PVDF压电悬臂梁结构产生振荡，根据压电效应，压电层的变形使其表面聚集电荷，形成响应电压。

图1 压电涡激振动(PVIV)流速传感器示意图

1.2 流－固－电耦合模型

由于气流经圆柱体产生涡旋后，后方的气流流动基本处于湍流状态，流场的分布复杂，因此，笔者结合计算流体力学(CFD)以及压电效应进行数值模拟，分析绕流体直径、与压电传感距离对低空气流速检测的影响规律。

1.2.1 理论模型

压电传感结构感知流体流动是一个多物理场耦合的复杂过程，主要包括流场、力场、和电场的综合作用。流场产生的压强转化为压力作用在悬臂梁表面产生结构变形并引起其压电层变形，根据压电效应产生电荷，计算模型中通过机电耦合方式将产生的电荷全部聚集在悬臂梁表面，最终转化为瞬态电压。变形体形状的改变将改变流场，其中的流固耦合面可由振动和流场控制方程来描述，当流场流速小于0.3马赫，流场被认为是不可压缩，这种不可压缩的牛顿流体介质可由连续性方程(1)和N-S(Navier-Stokes)方程(2)描述，方程如下所示:式中:p为流场压强，ρ为流场密度，vi为速度矢量，τij为应力张量，Skk为应变率张量。

式(1)和式(2)在模型中圆柱绕流体表面以及悬臂梁表面设定为无划移边界。

在压电材料厚度极化的线性Euler-Bernoulli梁假设下，机电耦合的本构方程为一维:

式中:下标1和3分别表示梁的长度和厚度方向；T1为应力；S1为悬臂梁长度方向的应变；D3为电位移；E3为通过压电层厚度的电场；cE11为恒定电场下的弹性刚度；εS33为恒定应变下的介电常数；e31为压电常数。式(1)~(4)形成了一个控制传感器气动－机械－电的耦合方程组，需对未知量(vΩ、pΩ、T1和D3)进行求解。笔者建立单自由度系统的动力学方程和机电耦合方程，二阶非线性范德波尔方程和高斯定律耦合如下所示:

式中:m为悬臂梁的质量，c为悬臂梁结构阻尼，k为刚度系数，Fy为流场作用在悬臂梁y方向上的瞬时压力，θ为机电耦合项，R为外接电阻，U为外接电阻电压，Cp为悬臂梁压电层电容，yt为压电梁顶部y方向瞬时位移。开路分析时，外接NI采集系统的电阻值无穷大(R＝∞)，可获得压电梁顶部位移与开路电压关系:

通过控制方程(1)、(2)、(5)~(7)可获得涡激振动产生的电压与流场流速之间的关系。根据傅里叶变换公式:

式中:U(t)为压电信号的时域值，U(f)为该信号的频域值。本文通过LabVIEW窗口采集输出信号。

1.2.2 仿真计算

将上述PVIV流速传感器简化为一个二维物理模型，如图2所示，其中，D为圆柱型涡流发生体直径，计算域为25D×5D的矩形，压电悬臂梁位于圆柱的中轴线上，左端固支。模型中，v范围在0.3 m/s~2.5 m/s，D范围在30 mm~70 mm，即雷诺数在500~9 800之间。选取空气域材料参数，采用SIMPLE求解器，进行瞬态分析，计算材料参数如表1所示。采用三角形非结构化的网格划分，在圆柱和PVDF压电梁的核心区域网格分布较密集。

图2 网格和边界条件示意图

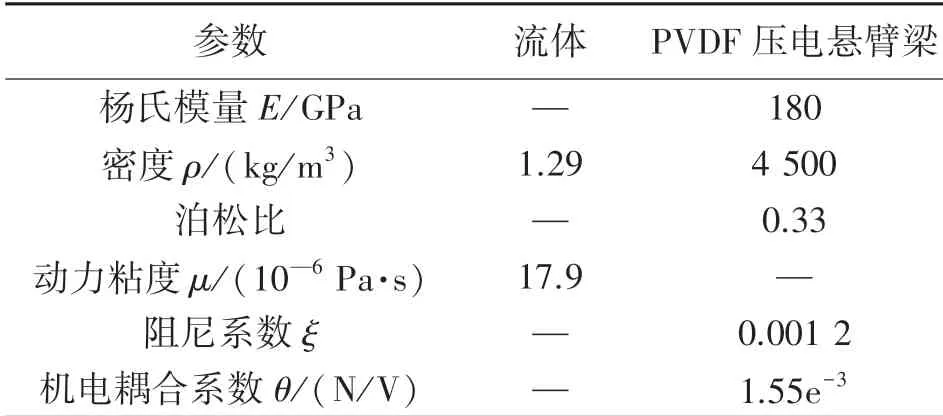
表1 材料参数

2 风洞试验

试验在低速风洞进行，测试平台如图3所示。采集的压电信号通过电荷放大器与NI数据采集卡相连，运用LabVIEW对信号进行ADC数模转换、滤波，频谱分析(FFT变换)；通过激光位移传感器采集涡激振动时压电梁末端的y向位移。最终在计算机中显示PVDF压电梁振动的时域曲线和频谱曲线。重点探寻压电传感距离在不同圆柱绕流体直径尺寸和流速变化的条件下对流场感知特性的影响规律。试验条件如表2所示。实验中，由50 mm到170 mm，间隔10 mm依次测量不同距离下的涡街响应信号。

图3 风洞测试

表2 试验条件

3 计算与测试结果分析

通过卡门涡街理论，笔者获得了涡街产生的流速条件和圆柱绕流体直径范围。

式中:μ为空气动力学粘度，St为斯特劳哈尔数，f为涡街脱落频率。当雷诺数在的范围内，涡流会以一个相对稳定的频率周期性脱落，根据流速条件和圆柱直径范围，可得出在该条件下的雷诺数范围为500~9 800，满足产生涡街脱落的条件。

图4为流速为2 m/s，圆柱直径为30 mm下，产生涡街脱落的特性。由图可知，涡街的交替脱落需要经历一个生长、成熟、衰退的过程。PVDF压电悬臂梁因此产生信号的传感强度与传感距离有关，由此验证了本文利用涡街传感的合理性。

图4 涡街脱落特性

图5 展示了升/阻力系数与传感距离和雷诺数的关系，文中PVDF压电悬臂梁左端固支，自由端在涡流中受到旋涡激振力的作用而产生y方向的周期性振荡。图5(a)为Re＝838，L＝50 mm时的流场升/阻力曲线，由图可知，在计算时间约3 s~5 s流场基本稳定。图5(b)升力系数与雷诺数Re，L之间的仿真关系。可知随Re增大，流场湍流强度增强，此时压电悬臂梁表面所受的压力增加，升力增大，在L＝50 mm时，幅值达1.1。值得关注的是，在相同雷诺数下，随传感距离的增大，升力系数随之下降，升力场呈现衰减的现象。其中，在L＝50 mm，即压电悬臂梁与圆柱绕流体之间距离最近时，其升力系数最高，反映流场波动最剧烈，其原因是悬臂梁的位置在涡街生长区，因此压电悬臂梁靠近圆柱体区域出现涡旋回流，造成的压力对压电悬臂梁的受力和振动产生增强的作用。此外，L＝50 mm~70 mm范围内，升力系数曲线整体下降不明显；L＝70 mm~110 mm范围内，升力系数曲线出现交叉的现象，说明该区域流场波动变化相似，此时PVDF压电悬臂梁的位置往往是涡街成熟区，适于形成稳定的涡街；L＝110 mm~130 mm范围内，其升力系数曲线整体下降明显，场流动性大幅下降，此时雷诺数为600，其升力系数下降至0.3，此时悬臂梁的位置往往是涡街衰退区。

图5 升阻力系数值变化

图6 展示了在流速为2 m/s，圆柱直径为30 mm条件下，传感器件位移响应特性。由图可知，流场作用3 s后，悬臂梁产生的y方向振荡逐渐稳定，该结果验证了图5(a)中流场升/阻力与时间的关系。受涡街作用，悬臂梁自由端部产生的y向位移最大；对比图5中计算位移曲线和通过激光位移传感器测得的实验位移曲线发现，实际测量的振荡曲线的幅值略小于计算幅值，同时前者的震荡频率(13.8 Hz)略小于后者产生的震荡频率(14.0 Hz)，原因在于计算设置的阻尼比与实际值有误差，然而由于误差较小，实际测量的震荡曲线与计算的到的大致一致，因此证实本文中流固耦合计算的准确性。

图6 当v＝2 m/s，D＝30 mm时，传感器件位移响应特性

图7 给出了圆柱绕流体直径为30 mm时，入射流速与PVDF悬臂梁感知涡街频率之间的关系。笔者主要对比卡门涡街理论值，仿真计算值与实验值。如图可知，计算值相比理论值，其与实验值更为接近，其更加准确的反映实际情况下的涡激振动时产生的涡街现象，进一步说明本文仿真计算的合理。其中，流速为1 m/s时的实验与计算时域曲线(图7(b)和7(c))可知，仿真计算下的PVDF压电悬臂梁产生的电压响应信号稳定，在涡街稳定后其电压幅值随时间几乎恒定，这说明此时悬臂梁在y方向的振荡幅值稳定；而对比图7(b)可知，实际条件下采集的电压时域曲线在幅值大小上随时间波动较为明显，即周期内的U峰－U峰值往往不稳定，在该曲线上会叠加包括电路干扰，工频干扰，以及流场对压电梁产生的x方向的振动影响。在此情况下，若根据前人[20]采用提取电压的U峰－U峰值、0－U峰值或Urms的方法来表征压电梁感知涡街的特性往往并不准确，而通过提取功率的方法更为准确，因此本文采用通过提取频域曲线中涡激频率下的功率表征涡街的传感强度。此外，由图7可知，仿真中，PVDF压电悬臂梁可检测的流速为0.3 m/s，此时该悬臂梁产生的振动约为2.0 Hz，该值与理论值及实验值接近，进一步说明了本文仿真计算的合理。

图7 当D＝30 mm时，压电传感器件对流速的响应特性

图8 为传感强度(功率P)在不同传感距离下的分布曲线。给出了D＝30 mm，入射流速依次为0.5 m/s，1.0 m/s，2.0 m/s时的实验及计算结果。同时根据式(8)，P值由对应时域曲线通过傅里叶变换(FFT)转换而来。图8(a)可知，同一绕流体直径下，流速越大，其P随传感位置的变化规律基本一致，即均在L为90 mm附近最大，反映出在相同区域PVDF压电梁测量的信号强度达到最大；同时反映，最佳传感距离(Losr)与入射流速大小无关，分析原因，根据卡门涡街理论，笔者认为这是由于涡街交替脱落时旋涡方向对压电梁产生的影响，即旋涡y方向的速度引起振荡作用(参考图9周期内的y方向流场速度可知)，与x方向，即入射流速方向无关。值得注意的是，由图8(b)~图8(d)发现，在相同直径下，随流速增大，流场对压电梁产生的激频成分更为复杂，这与图5(b)相符，即随Re增大，流场湍流强度增强，反映流场波动更加剧烈。但是对于产生涡街的频率稳定且与理论(式(10))一致，进一步说明了本文采用功率来表征传感强度的合理性。此外，观测图8(a)可知，L超过110 mm时，P值均下降，分析原因，根据涡街理论，由于黏性的耗散，此时旋涡逐渐衰退，所以最佳的传感位置应在涡街的成熟区附近。

图8 当D＝30 mm时，不同流速下的涡街能量分布

图9 振动周期下，PVDF压电悬臂梁在y方向的涡流云纹图

图10 为传感强度(P)在不同传感距离下的分布曲线，展示了低流速情况下，即v＝1 m/s，绕流体直径依次为30 mm，40 mm，50 mm时的实验及计算结果。由图10(a)可知，P随传感距离L的分布规律有所不同。当D越大，Losr越大，即旋涡越远离绕流体。例如当D＝30 mm时，Losr＝90 mm；当D＝40 mm时，Losr＝110 mm；当D＝50 mm时，Losr＝130 mm。值得注意的是，由图10(b)~图10(d)发现，在相同v下，随D值增大，流场对压电梁产生的激频成分更少，分析原因，可能是由于随着D值增大，在CCT两侧产生的交替旋涡相互之间的作用减小，使得流场的波动减小所导致的。

图10 当v＝1 m/s时，不同绕流体直径下的涡街能量分布

图11 展示了当v＝0.5 m/s，D＝30 mm时，一个振动周期下涡街压强云纹图以及悬臂梁的变形情况。可以直接看出，悬臂梁在涡街中受到周期下的漩涡激振力而产生振荡现象。其中悬臂梁两侧的压强差是导致悬臂梁的偏转的直接原因，而压强差是由于涡街通过悬臂梁产生的。与此同时，压强差产生了流场的升力，使得悬臂梁得到了向上及向下运动的加速度。不仅如此，悬臂梁自由端振幅随时间的增长最快，达到最大振幅时，振动速度最小。此外，一个振动周期内，悬臂梁产生了两次振动方向的改变，使得悬臂梁周围流场也发生了周期性的改变，PVDF压电悬臂梁与流场的相互作用形成了较为稳定的振动规律，振动周期保持不变。

图11 PVDF压电悬臂梁的振动周期下涡街压强云纹图以及悬臂梁变形图

图12为最佳传感距离与流速及绕流体直径之间的计算及实验关系。由图12(a)可知，Losr随D值增大逐渐增加，且近似线性关系。同时，测量曲线与计算曲线一致。分析原因，根据图4及式(10)，最佳传感距离应该在旋涡的成熟区，D增大时，其两侧剪切层之间距离变大，其相互作用变慢，使漩涡的脱落频率减小，使得旋涡产生位置距绕流体越远，即最佳检测位置越远离圆柱绕流体。由图12(a)进一步可知，Losr与v无关，这与图8(a)的分布曲线一致。

图12 最佳传感距离与流速及绕流体直径之间的关系

图13 为最佳传感距离下的P值(Posr)与v，D之间的计算及实验关系。由图13(a)可知，Posr随v增大而递增，同时随D增大而递增；同时，测量曲线与计算曲线保持一致。分析原因，根据式(9)，由Re与v×D成正比关系，Re增加，导致其升力系数增大，即反映流场波动越剧烈，此时结构表面所受压力增加，导致PVDF压电梁的振荡幅值变大，产生的压电功率越高。其中图13(b)显示，当v＝2.5 m/s，D＝70 mm，Posr约为10×104mW；当v＝0.5 m/s，D＝30 mm，Posr约为8×102mW。可推测，若流速和直径同时分别小于0.5 m/s和30 mm，产生的Posr将小于8×102mW。然而如果用时域电压的U峰－U峰值、0－U峰值或Urms的方法来表征压电梁感知涡街的特性往往会被噪声干扰，难以提取特征量。这也进一步证明了本文采用提取最佳功率来表征涡街在传感距离上传感强度的合理性。

图13 最佳传感距离下的功率与流速及绕流体直径之间的关系

4 结论

设计和研究了一种基于涡激振动的压电传感装置。通过响应信号分析了最佳传感距离和功率与绕流体直径和流速的变化规律。建立了流－固－电耦合数值模型，构建了流速测量的新方法。采用通过提取频域曲线中涡激频率下的功率作为涡街的传感强度。实验和仿真结果表明:增大绕流体直径可以使最佳传感距离和功率线性增加；然而，在最佳传感距离不变的情况下，增大流速可以提高功率。通过流场分析得出了采集信号在Losr下最优的本质原因为:在该处，涡街成熟且脱落稳定、升力系数稳定。此外，风洞实验验证该基于涡激振动的柔性压电悬臂梁流速感知特性。结果表明:该传感器件能有效地测量低至0.3 m/s流速；当v＝2.5 m/s，D＝70 mm，Posr约为10×104mW；当v＝0.5 m/s，D＝30 mm，Posr约为8×102mW。该提取涡街信号的方法和规律可以解决传统的涡街信号微弱以及低流速难测量的问题，扩大了该类流速传感器的应用范围，为高灵敏，快响应的流速传感器件的设计及测量提供了新的探测方法。