基于最小二乘数据拟合的微小压力传感器仿真设计∗

宫凯勋雷 程∗董志超赵珠杰熊继军齐 蕾

(1.中北大学仪器科学与动态测试教育部重点实验室，山西 太原030051；2.北方自动控制技术研究所，山西 太原030051)

在MEMS器件的设计加工中，通常具有周期长、费用高等特点，可靠的仿真计算在器件的设计中十分重要[1]。硅压阻式压力传感器因其灵敏度高、精度高、体积小、动态频响高等优点一直作为MEMS压力传感器领域的热门应用与研究对象[2]。压阻式压力传感器敏感膜上的力学敏感器件受压后阻值的变化决定着传感器的输出[3－5]，而阻值的变化与应力有关。普遍的对于仿真计算得到的压敏电阻上应力的处理是取其中心一点的应力值进行估算或者通过定义路径计算路径上压敏电阻的应力积分，再除以压敏电阻的长度求得压敏电阻所在位置的平均应力。

上述算法都有其局限性，忽视了压敏电阻整体的应力分布不均匀的性质。在对压阻式压力传感器的仿真设计中通常将承压膜看作薄板结构[6]，施加垂直于板面的应力时，其应力的分布均以中面为对称面，且在中面处降至最低。压力传感器特别是微压传感器因其膜厚与压敏电阻的高度比值较小，不可忽视压敏电阻延高度方向上应力的变化。为解决上述问题，本文采用基于最小二乘法的多项式拟合方法对压敏电阻横截面方向上的应力进行函数拟合，求得在固定z轴数值的平均应力，通过对不同z轴坐标下压敏电阻平均应力的计算，拟合出z轴对应力的函数关系，再计算压敏电阻的整体平均应力，为压阻式压力传感器提供更科学的设计计算方法。

1 算法原理

1.1 弹性薄板理论

压阻式压力传感器上敏感膜作为弹性感压部件，一般情况下，敏感膜在理论分析时被看作是在厚板与薄膜之间的薄板结构。根据弹性力学理论，其在分析时满足小挠度理论的模型，弹性薄板小挠度理论的基本假设:板弯曲时，板中面内各点只存在垂直方向上的位移没有平行中面方向上的位移；弯曲变形前垂直于薄板中面的直线，变形后仍垂直于弹性曲面且长度不变；薄板各层的纤维在变形前后均互不挤压[7]。

基于这些假设，对于薄板问题的求解最重要的是对于薄板挠曲函数ω(x，y)的求解，图一所示为在方形薄板施加面载荷。

在薄板上建立直角坐标系，其挠度变化可表示为:

式中:D为弯曲刚度，可用式(2)表示；p为薄板所受的压力载荷。

式中:E为材料的弹性模量；v为泊松比；t为薄板厚度。

薄板的边界条件为x＝0，x＝a，y＝0，y＝a，即:

代入式(1)可解得薄板的挠度为:

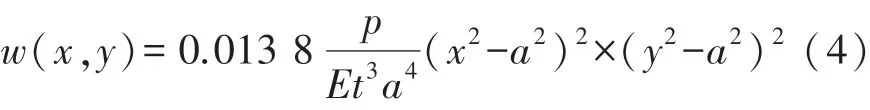
薄板上任一点(x，y)延x方向应力δx与延y方向的应力δy为:

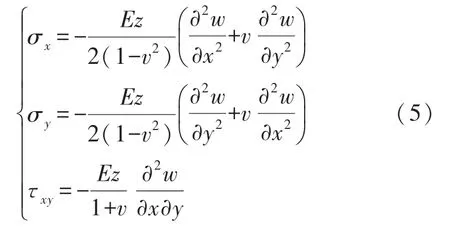
由式(5)可知，主要的应力分量延z轴线性分布，故可先对(x，y)坐标与应力值拟合，再对不同Z坐标下的平均应力值做拟合积分得到更为准确的仿真压敏电阻平均应力计算值。

1.2 最小二乘法拟合

数据拟合的目的是利用最小二乘方法，将基于模型函数所计算出的数值与观测量之间的残差平方和最小化[8－11]。

以本文采用的三元二次多项式方程拟合为例，对于方程:

有N组具有相同精度的数据(xi，yi)，其中i＝1，…，N；xi，yi都是精确的，对与之相对应的zi值进行预测。用最小二乘法估计参数时，要求观测值zi的偏差加权平方和最小。用泛函误差δ表示:

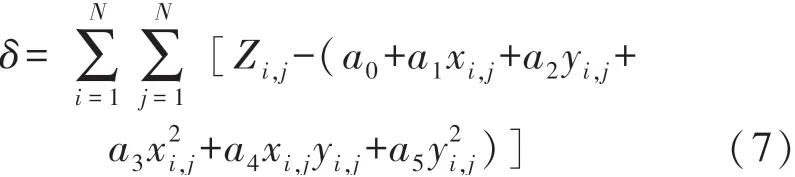
a0，a1，a2，a3，a4，a5的值影响着δ的大小，求取δ的最小值，即对a0，a1，a2，a3，a4，a5分别进行求偏导，转化为一个泛函求极值问题。

2 有限元仿真

COMSOL Multiphysics是一款功能强大的多物理场仿真软件，用于仿真模拟工程、制造和科研等各个领域的设计、设备及过程。其界面简洁，模型建立简单且仿真计算后的数据导入与导出都极为便捷。本文采用comsol软件对压敏电阻应力值进行仿真计算。

2.1 建模与网格划分

压阻式压力传感器的敏感膜一般为方型膜与圆型膜，方形薄板的最大应力比圆形薄板的最大应力大，有利于获得更高灵敏度的压力传感器，所设计的微压传感器采用方形膜作为感压膜面。

在comosl软件中，一般的通过布尔操作对几何体进行结构建模的方法对于计算后网格数据提取与处理较为困难。为解决这一问题，采用各结构独立建模，最后通过构成联合体的方式形成完整的器件结构，为网格划分与数据的后处理提供了便利。

敏感膜模型尺寸设计为460μm×460μm×7μm，压敏电阻尺寸为65μm×13μm×1.5μm。压敏电阻位置在膜边缘10μm处。单晶硅材料属性包括杨氏模量170 GPa、泊松比0.3、密度为2 329 kg/m3。传感器采用惠斯通半桥结构，建模时对垂直方向与平行方向的一个压敏电阻进行网格加密剖分。

各部分单独建模的好处是在划分网格的过程中可较好地控制局部网格的密度，网格划分采用用户控制网格，将压敏电阻网格延Z轴方向划分10层，X、Y轴方向自由剖分，得到延Z轴分层结构的四面体网格，结构剩余部分采用自由四面体网格自适应划分，图2为网格刨分结果图。应力从敏感膜面到与支撑体相连边界处后迅速衰减，将实际模型简化为下图结构以减少不必要的计算。边界条件:敏感膜上表面施加40 kPa的压力，结构底部采用固定约束方式。

图2 网格刨分图

2.2 有限元分析结果

从图3可以看出，垂直膜面位置压敏电阻应力分布结果与弹性力学分析结果一致，应力延中面对称分布，且中面位置应力降到最低。在距离膜面1.5μm位置上的压敏电阻应力下降为膜表面处应力的一半，应力延z轴方向上的变化已不能忽略。

图3 沿膜厚方向von Mises应力分布

从图4垂直膜边压敏电阻表面应力等值线图可以得出，压敏电阻表面不同位置应力大小也不同，故在压力传感器设计中必须对压敏电阻整体结构的应力分布进行考虑。

图4 压敏电阻纵向应力横向应力差值分布图

3 多项式数据拟合处理

常用到的数据拟合主要有线性回归拟合与多项式拟合，线性回归拟合要求自变量与因变量之间具有线性关系，多项式拟合较线性回归拟合总体上更为灵活，可以模拟一些相当复杂的关系[12]。在数据范围内，多项式拟合方法可以提供很好的拟合效果，但在数据范围外可能会大范围发散。压敏电阻不存在对数据范围以外进行预测，其上各点位置的应力值都可以通过仿真计算得到，使用MATLAB软件通过基于最小二乘法的多项式拟合方式来对压敏电阻平均应力进行计算。

在COMSOL软件的后处理部分，通过域选择导出压敏电阻部分的计算数据集，并对不同Z坐标的数据进行分类，将处理好的数据通过importdata函数导入到MATLAB中。

对垂直于膜边压敏电阻应力进行处理，在Z坐标为0即压敏电阻顶面位置时，图5为采用二次多项式拟合方式得到的结果，其中离散点为COMSOL计算得到的原始数据，曲面为拟合得到的结果。

图5 x，y坐标值与应力值拟合

拟合得到的多项式函数为:

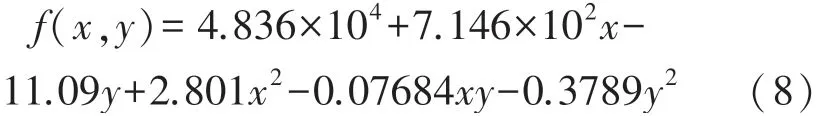
拟合确定系数R-square:0.999 8，接近于1，表明该方程可以很好的对散点数据进行表达。

将原始数据坐标代入到拟合得到的函数进行计算，通过MATLAB里plot3函数作图与原始数据进行对比，从图6来看，原始数据与拟合数据在同一曲面上，可以忽略由离拟合得到的函数的计算值与仿真得到的数据误差。

图6 拟合计算值与仿真计算值对比

在MATLAB语言中，求符号函数的定积分是使用int函数，其调用格式如下:int(F，x，a，b)。a表示定积分的下限；b表示定积分的上限；使用int函数对表达式进行积分，再除以电阻条截面积可得到固定z坐标下压敏电阻截面上的平均应力，表1为计算结果。

表1 施加40 kPa压力不同高度下压敏电阻截面的平均应力

Z轴坐标与垂直膜边压敏电阻计算出对应的平均应力进行拟合，图7为拟合得出的曲线。

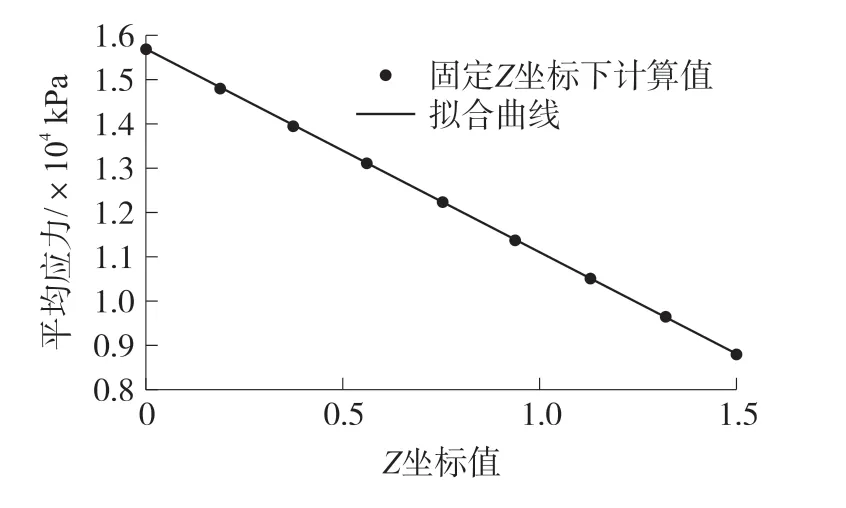
图7 Z坐标值与应力值拟合

拟合得到的函数为:

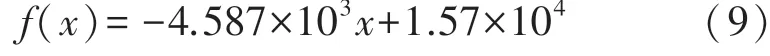
拟合确定系数为R-square:1。

对拟合得到的函数积分可求得在压力为40 kPa时，垂直膜边压敏电阻平均应力值为12 261 kPa。重复上述计算，得到平行膜边压敏电阻平均应力值为19 787 kPa。

4 传感器输出计算

基于上述方法，计算得到不同压力载荷下各压敏电阻的平均应力值，表2为计算结果。

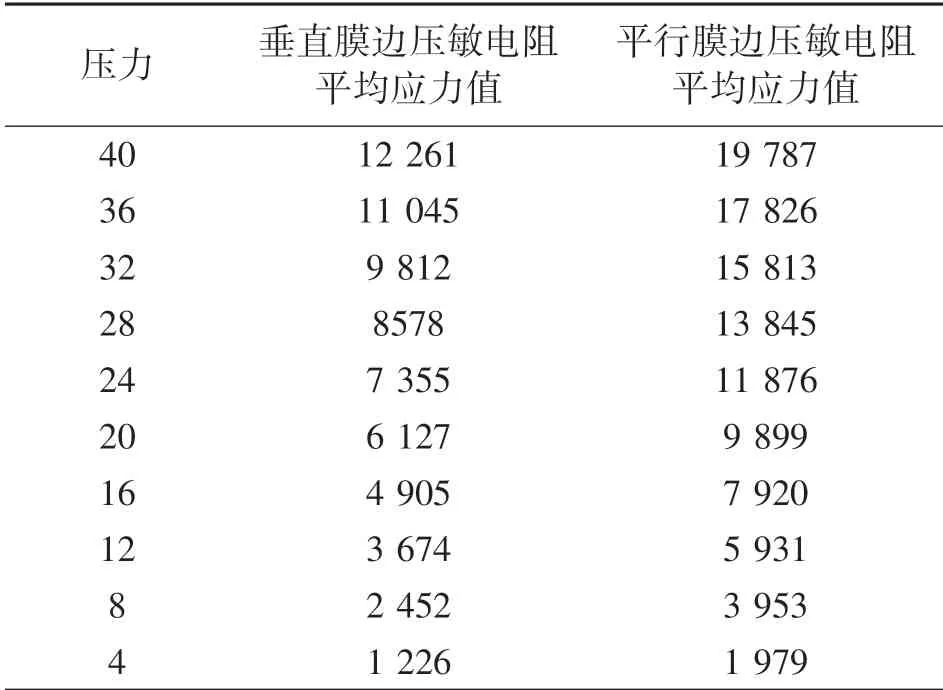
表2 不同压力载荷下各压敏电阻的平均应力值 单位:kPa

对于采用半桥方式实现压敏电阻内部连接的压力传感器，其电压输出公式为:

图8所示为在输入电压为3.3 V时灵敏度的仿真计算结果。

图8 分层截面积分法压力与输出电压曲线

拟合得到的函数为:

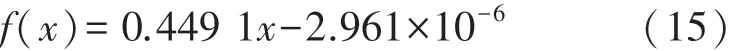
确定系数R-square:1

得到在电压为3.3 V时，所设计传感器灵敏度为0.4491 mv/KPa。

若采用中心点算法，提取电阻条表面中心点位置应力值，在40 kPa下，σa＝25 543 kPa，σb＝14 671 kPa，根据式(14)计算得输出电压为22.5 mV，图9中虚线为中心点法压力与输出电压曲线，得到采用中心点法设计的传感器灵敏度为0.562 8 mV/KPa。采用路径积分法，提取电阻条表面中心线处应力做积分，计算得到在40 kPa下，σa＝25 298 kPa，σb＝15 775 kPa，根据式(14)计算得输出电压为23.0 mV。为与中心点法计算输出曲线区分，将其输出曲线零点变为10 mV，图9中实线为路径积分法压力与输出电压曲线，得到采用路径积分法设计的传感器灵敏度为0.575 mV/KPa。

图9 中心点法与路径积分法压力与输出电压曲线

5 芯片加工与测试

芯片选用顶层硅6.5μm、埋氧层厚度0.5μm、片厚300μm的SOI作为衬底；采用离子注入方式掺杂形成压敏电阻；扩散炉内温度1 000℃、时间20 min重掺杂构建欧姆接触区；磁控溅射钛、铂、金并在温度500℃、时间5 min高真空下退火形成欧姆接触；通过刻蚀至SOI埋氧层来精准控制敏感膜厚度，采用阳极键合工艺温度380℃、压力1 200 N、电压800 V下实现硅－玻璃键合形成表压参考腔。图10所示为芯片正面结构显微镜观察。

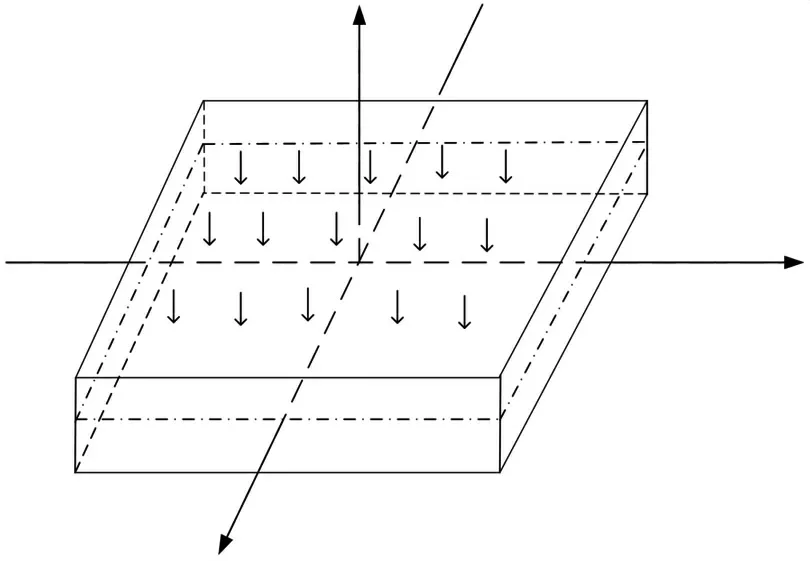
图1 方形板直角坐标系

图10 芯片正面结构

压力传感器芯片封装在特制的不锈钢测试管座，安装在常温压力测试平台气压泵接口，使用高精度万用表测量记录实验数据，图11所示为实验测试结果，灵敏度为0.455 2 mv/kPa，与设计计算结果偏差为1.34%，采用中心点法与路径积分法的设计偏差分别为23.64%与26.32%。采用分层截面积分方法可极大提高仿真设计精度。

图11 不同压力下电压输出结果

6 总结

为减小压阻式压力传感器特别是微压传感器设计结果与实际制作测试的误差，本文提出一种分层截面积分的方法。通过对压敏电阻与敏感膜面分别建模实现对局部网格的精确加密与局部数据的导出，基于最小二乘法的多项式拟合方法实现对压敏电阻离散点应力值的拟合计算，将传统的中心点算法(零维)、路径积分法(一维)提高到了分层截面积分(三维)的程度，提高了仿真计算结果的可信度，所设计的传感器灵敏度与实际测得灵敏度偏差为1.34%。该方法为压阻式压力传感器特别是微小压力传感器的灵敏度计算制作提供了更为可靠计算方式，在压阻式压力传感器设计中具有现实意义。