送风仰角35 °、大风速下净化器PM2.5净化时间预测模型研究
金梧凤 董战伟 王 成 王志强
(天津商业大学,天津市制冷技术重点实验室 天津 300134)
引言
目前室内污染已经成为影响人们健康的主要因素,造成室内污染的主要原因除了受室外空气质量的影响外,还有人类自身的活动[1]。空气净化器作为可有效去除室内颗粒物,保证室内空气质量的环境电器,备受人们青睐[2]。使用空气净化器是目前室内污染治理、改善空气质量、提升居住或办公品质较为常见的方法[3]。室内设置空气净化器,就是要提高室内空气品质[4]。但是,在空气净化器的实际运行过程中,当环境条件、净化器参数发生变化时,室内不同位置处PM2.5净化时间不同,因此,有必要研究不同条件下房间不同人员位置处的PM2.5净化时间。
近年来,许多学者针对室内PM2.5颗粒物浓度分布和空气净化器净化效果进行了大量的研究。李擎[5]针对空气净化器典型摆放位置、送风角度以及送风风速对室内流场以及PM2.5净化效果的影响进行了数值模拟分析;刘玉荣[6]分析了室内相对湿度、房间气密性、室内外压差对室内细微颗粒物浓度变化的影响;李擎、李擎[7]等人以上送侧回式空气净化器为例,发现当净化器位于渗透风下风向的位置时,净化效果最差,位于侧向位置时净化效果最好;张艳菊[8]等人研究了空气扰动对净化器去除颗粒物效果和CADR的影响,结果显示,空气扰动在一定程度上提升了空气净化器的净化能力,增大了CADR;白莉[9]等人对4台空气净化器进行了实验研究,分析了不同相对湿度下空气净化器的现场净化效率、洁净空气量、有效净化效率和净化能效,以及细颗粒物(PM2.5)的自然衰减规律与净化衰减规律。
综上所述,目前针对空气净化器智能化控制的研究相对较少,不能实现人员位置处的优先净化。本文在空气净化器送风仰角35 °、最大风速模式下,研究了房间尺寸、吹风角度、PM2.5初始浓度、人员位置等影响因素对PM2.5净化时间的影响,最后通过SPSS软件对模拟数据进行统计回归分析,得到PM2.5净化时间预测模型,为空气净化器智能控制方案的提出奠定了基础。
1 PM2.5净化时间影响因子分析
参考ANSI/ASHRAE 62.1-2013《可接受的室内空气质量通风标准》相关规定,推荐室内PM2.5浓度值限值为15 μg/m3[10]。故定义PM2.5净化时间为室内PM2.5浓度由初始浓度降到15 μg/m3所需要的时间,记为t,单位min。在对空气净化器的PM2.5净化时间的研究过程中,首先应进行PM2.5的自然沉降研究,得到PM2.5的自然沉降时间,在此基础上,再进行空气净化器运行状态下的PM2.5净化研究。
1.1 影响因子的确定
本文根据净化器产品手册和相关规范,从室内颗粒物污染的质量守恒、室内净化不均匀性和气流组织三个方面进行影响因子分析。
1)质量守恒
根据空气净化器标准GB/T 18801-2015[11],室内的颗粒物污染满足质量守恒,如式(1)所示:
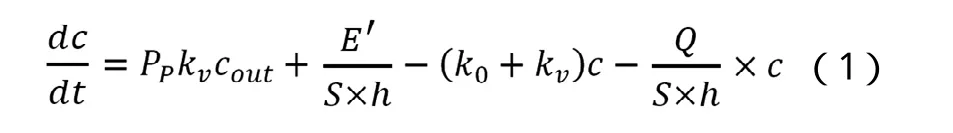
式中:
c—室内颗粒物污染物浓度,mg/m3;
PP—颗粒物从室外进入室内的穿透系数;
cout—室外颗粒物的质量浓度,mg/m3;
E′—室内污染源的产生速率,mg/h;
k0—颗粒物的自然沉降率,h-1;
kv—建筑物的换气次数,h-1;
Q—净化器去除颗粒物的洁净空气量,m3/h;
S—房间面积,m2;
H—房间高度,m。
其中参数PP、k0、kv、H均为定值,本文不考虑室内外污染源,即E′=0,cout=0。所以,将PM2.5初始浓度、房间面积确定为影响因子。
2)净化的不均匀性
由于空气净化器运行时,室内不同区域净化具有不均匀性,故需要考虑室内不同人员位置处的净化时间。因此,本文将通过人员角度和人员距离确定人员位置,其中人员角度为人员偏离空气净化器送风方向的角度,人员距离为人员与空气净化器的距离,如图1所示:β为人员角度、L为人员距离。
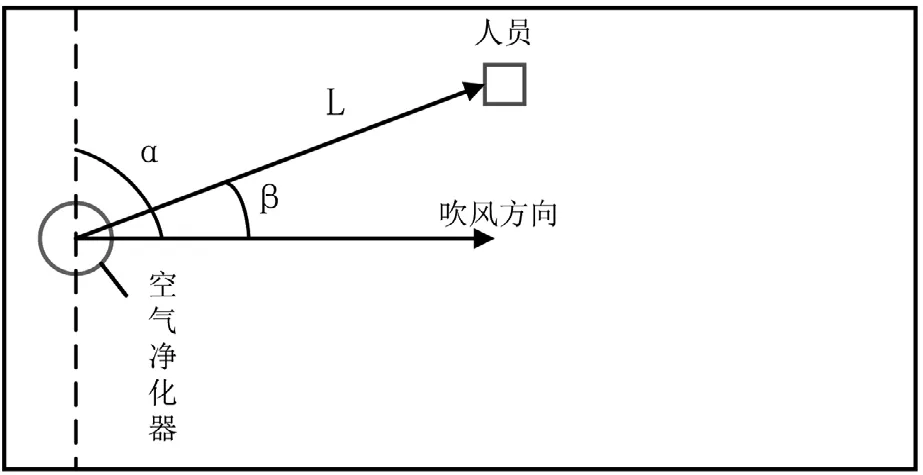
图1 吹风角度和人员位置示意图
3)气流组织
有关研究表明,在室内空气扰动工况下,空气净化器对粒径>0.3 μm的颗粒物去除效果提高[12]。所以,气流组织对室内颗粒物的净化具有很大的影响,故将房间长宽比、空气净化器吹风角度确定为影响因子。其中吹风角度定义为送风方向与出风口垂直于墙面的线在三维空间的夹角,如图1所示:α为吹风角度。
综上所述,本文最终确定PM2.5净化时间的影响因子为:PM2.5初始浓度ρ、房间面积η、房间长宽比Γ、吹风角度α、人员距离L、人员角度β。
1.2 影响因子的取值范围
通过查找相关资料与规范确定各影响因子的取值范围及模拟取值,如表1所示。

表1 影响因子的取值
2 实验研究
本实验按照国家标准设置标准实验舱,实验数据主要为模拟研究部分的边界条件设置和模型验证提供依据,同时也为后续建立预测模型提供数据支撑。
2.1 实验舱介绍
该实验舱由内舱和外舱组成,内舱尺寸为3 m×6.15 m×3.2 m。本文实验使用某型号空气净化器,其简图如图2所示。
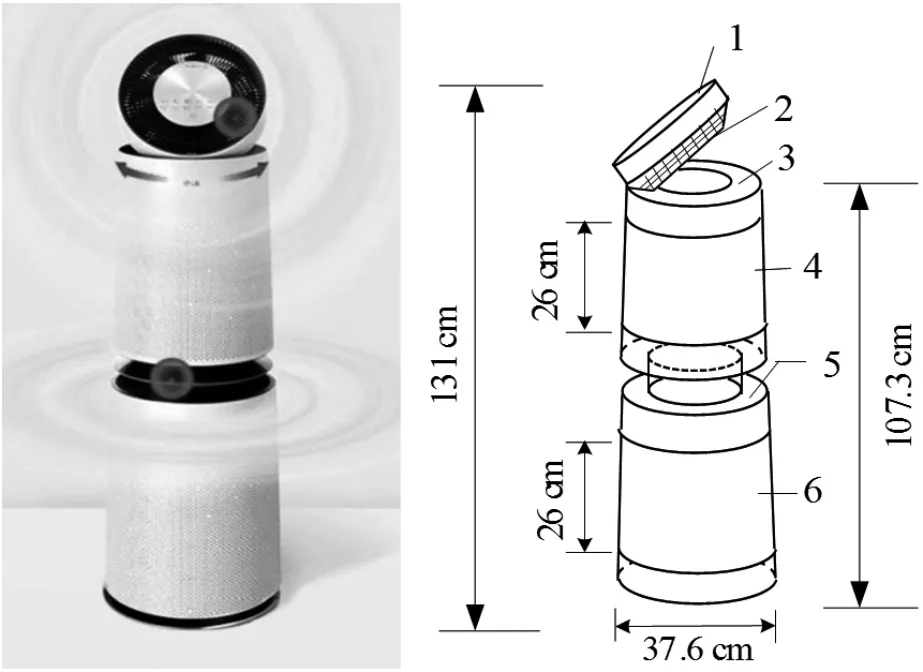
图2 空气净化器实物图与结构示意图
内舱内部设有颗粒物发生装置(点烟器),提供颗粒污染物;循环风扇,使颗粒污染物尽可能分布均匀;PM值/粒子计数器,测量室内PM2.5浓度。内舱内部示意图如图3所示。
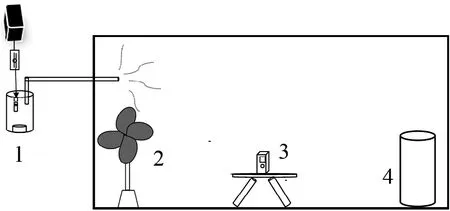
图3 内舱内部示意图
2.2 实验条件
依据空气净化器标准GB/T 18801-2015[11],其具体实验环境条件如表2所示。
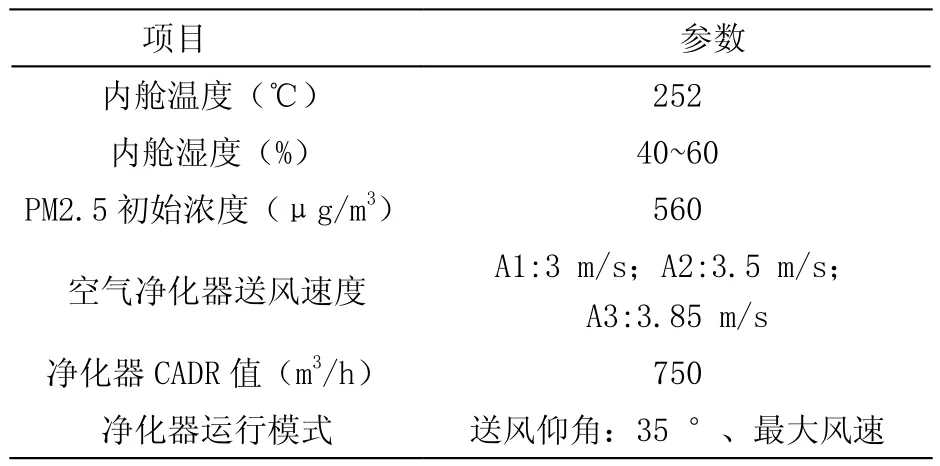
表2 实验环境条件
2.3 测点布置
为了保证测点数据具有代表性,本次实验分别对内舱中部和后部进行监测,两个测点分别距空气净化器2.5 m和5 m,高度为1.1 m(人员坐姿时呼吸区),如图4所示。
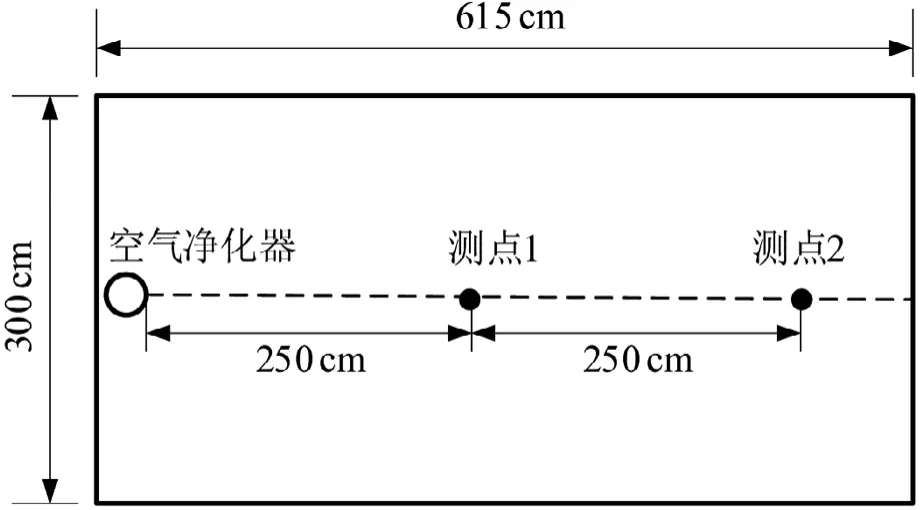
图4 实验舱测点布置
2.4 实验过程
2016年3月正式实施的GB/T 18801-2015《空气净化器》标准中对颗粒物CADR检测推荐的香烟尘源是红塔山牌经典150[11],故本次实验采用红塔山为室内提供污染物颗粒。
本次实验共分为三个阶段:准备阶段、稳定阶段和测试阶段。准备阶段:在进行实验前,将室内舱温度和相对湿度保持在设定值,并开启空气净化器对室内舱进行预处理,当室内舱PM2.5浓度低于15 μg/m3时关闭空气净化器,打开点烟器并点燃四根香烟,根据多次的测试结果,其室内的PM2.5浓度可以达到560 μg/m3左右。稳定阶段:打开循环风扇10 min,确保室内PM2.5分布均匀。测试阶段:打开空气净化器和PM值/粒子计数器,进行PM2.5浓度测量,并使空气净化器持续运行1 h,确保室内PM2.5被充分净化。
为了减小实验误差和保证准确性,本文进行3次重复实验,对实验结果进行比较,求取平均值。
3 模拟研究
3.1 模型建立及验证
3.1.1 物理模型
根据实验条件,建立与环境舱相同尺寸的房间几何模型(6.15 m×3 m×3.2 m),并根据实验所使用空气净化器的结构和尺寸建立净化器模型。参考表2的实验条件,将PM2.5初始浓度设置为560 μg/m3。
3.1.2 边界条件
1)壁面边界条件设置
实验舱壁面与空气净化器壁面均设置为无滑移边界,湍流度为5 %,壁面温度设置为绝热。
2)空气净化器送风口边界条件设置
空气净化器送风口设置为速度入口,湍流度为5 %。
3)空气净化器回风口边界条件设置
空气净化器回风口均设置为自由出流,湍流度为5 %。
空气净化器的净化效率设置为98 %。
3.1.3 模型验证
对所建模型进行计算,其测点布置与实验测点布置相同,最后将模拟结果与实验结果进行对比,分别对两个测点处净化过程中PM2.5浓度的变化进行最大误差和平均误差分析,如表3所示。
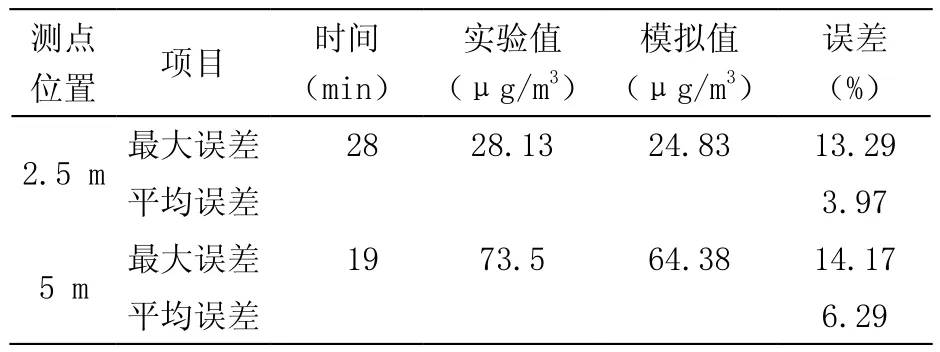
表3 误差分析
根据表4误差分析可知:两个测点处模拟与实验的最大误差均小于15 %,且平均误差小于7 %。主要原因有以下两点:
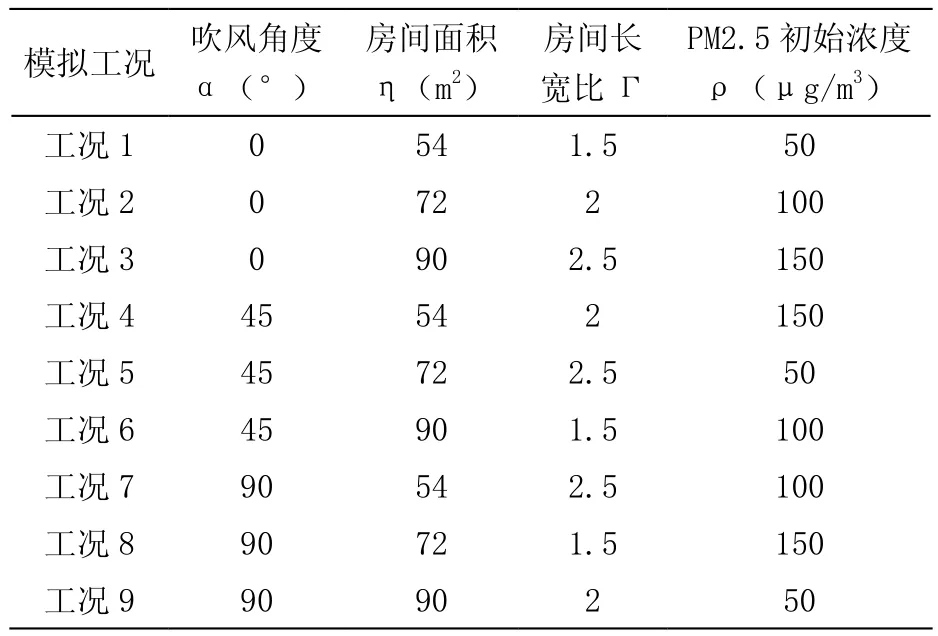
表4 模拟工况表
1)建立物理模型的过程中,对空气净化器进行了简化,忽略了壁面的无数蜂窝小口,导致回风阻力变小;
2)边界条件的设置中,壁面均设置为无滑移,忽略了粗糙度的影响。
综上所述,可认为所建模型是准确的,可使用此模型进行模拟扩展研究。
3.2 模拟扩展研究
由于实验条件的限制,为了更加全面分析各影响因子对室内PM2.5净化时间的影响,需要进行模拟扩展研究,为后续回归统计提供回归资料,也为后续建立预测模型提供数据支撑。
基于上述模型的验证,运用正交实验法,根据表1中影响因子的模拟取值,分别建立面积为54 m2、72 m2、90 m2,长宽比为1.5、2、2.5的九种房间模型,使用Fluent软件进行模拟扩展研究。
3.2.1 模拟工况的确定
模拟工况以吹风角度,房间面积,房间长宽比,PM2.5初始浓度4个影响因子通过正交实验法进行确定。具体的模拟工况如表4所示。
3.2.2 数值模拟测点布置
依据影响因子中人员距离L和人员角度β进行测点布置,前3.5 m每隔0.5 m设置一个测点,后续测点的间隔为1 m,高度都为1.1 m(人员坐姿时呼吸区)。模拟测点布置如图5所示(以模拟工况1为例)。
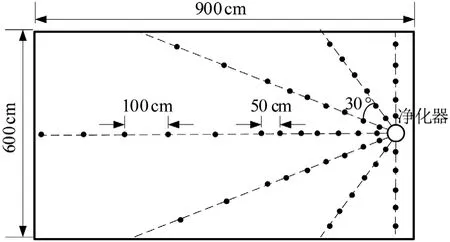
图5 模拟测点布置
3.3 回归资料的建立
对表4中设置的九种工况进行模拟计算,由于房间尺寸不同,每种工况的测点布置数量有所不同,故每种工况得到的净化时间数量不同,如表5所示。将每种工况得到的净化时间作为一组回归资料,共得到九组回归资料,总计381个净化时间。
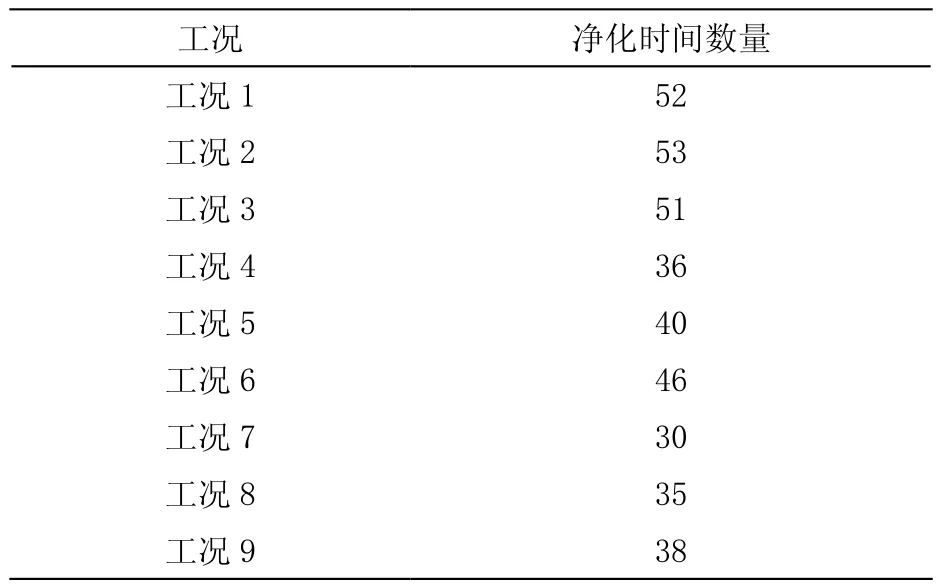
表5 回归资料统计
4 PM2.5净化时间预测模型建立
4.1 PM2.5净化时间回归分析
由模拟数据得到的回归资料如表5所示,采用SPSS软件对其进行多元线性/非线性回归分析,其分析结果如表6所示。
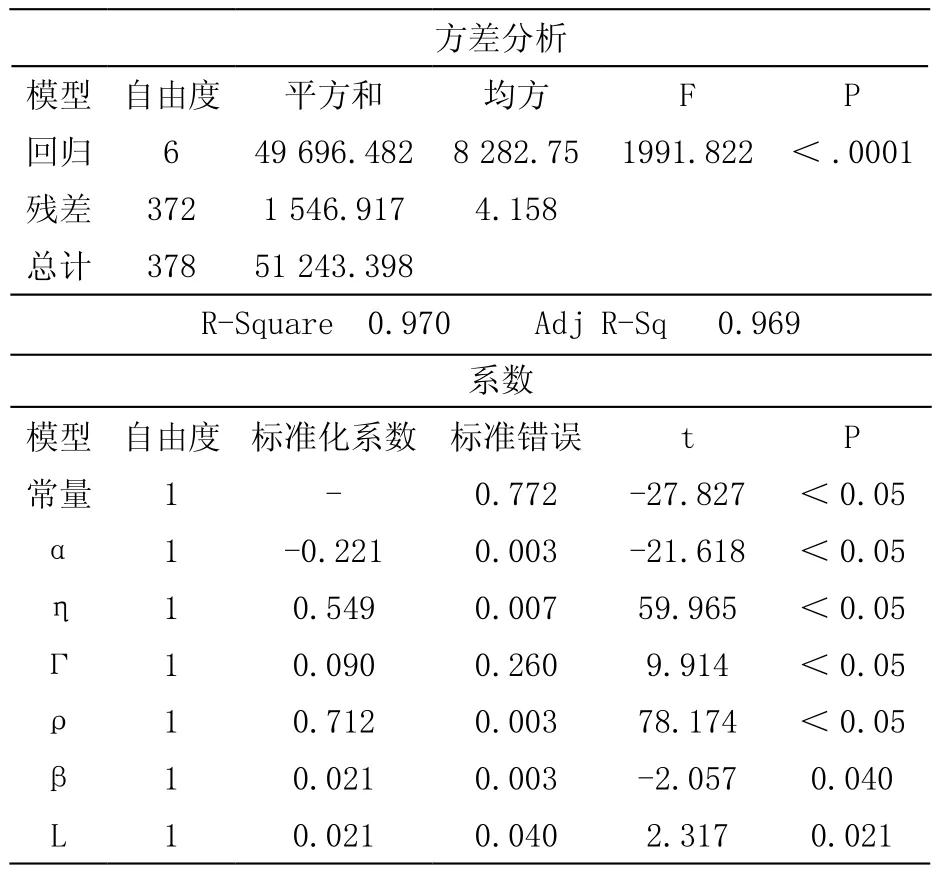
表6 多元线性回归分析结果
由表6可知,该回归方程的P值小于0.001,即回归结果非常显著;其中R-Square=0.970、Adj R-Sq=0.969,即拟合程度较高;自变量回归系数P值均小于0.05,即自变量都应保留。
通过以上分析,可以得到PM2.5净化时间t与各影响因子之间的关系式如式(2)所示:
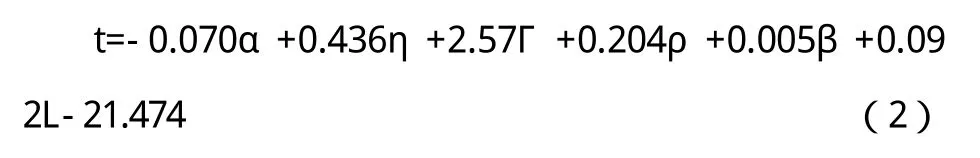
式中:
t—PM2.5净化时间,单位min;
其他各参数的取值范围见表1中各影响因子取值范围。
由式(2)可知,PM2.5净化时间分别与房间面积η、房间长宽比Γ、PM2.5初始浓度ρ、人员角度β和人员距离L呈正相关;与吹风角度α呈负相关。因为,当空气净化器吹风角度变小时,到达房间后部区域的风量较小,延迟了PM2.5净化时间。
4.2 净化时间预测模型验证
前面通过实验数据验证了模拟部分所建立模型的准确性,因此本研究使用模拟结果对净化时间预测模型进行验证。由于工况1、工况2和工况3净化时间数量相对较多,故选取此三种工况分别从不同人员距离和不同人员角度两方面对该预测模型进行验证。
4.2.1 不同人员距离
以人员偏离吹风方向90 °时不同人员距离的数据为例,对模拟值与预测值的净化时间做最大误差与平均误差分析,如表7所示。
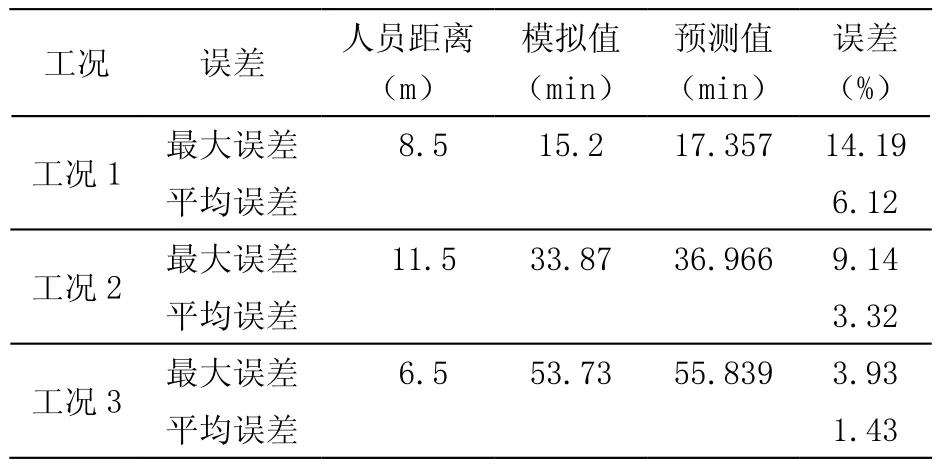
表7 误差分析
从表7中可以看出,PM2.5净化时间预测模型预测值和模拟值最大误差均小于15 %,平均误差均不超过7 %,因此可以认为PM2.5净化时间预测模型准确。
4.2.2 不同人员角度
以人员距离为2 m时人员偏离吹风方向不同角度的数据为例,对模拟值与预测值的净化时间做最大误差与平均误差分析,如表8所示。
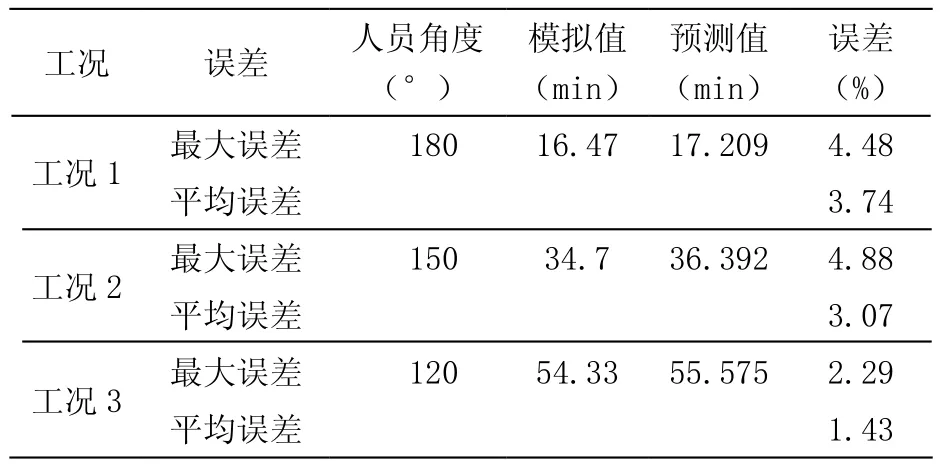
表8 误差分析
从表8中可以看出,PM2.5净化时间预测模型预测值和模拟值最大误差均小于5 %,平均误差均不超过4 %,因此可以认为PM2.5净化时间预测模型准确。
综上所述,认为回归分析中得到的PM2.5净化时间预测模型准确。
4.3 影响因子贡献率分析
根据表6得到的各影响因子标椎化系数,计算各影响因子的贡献率,如图6所示。
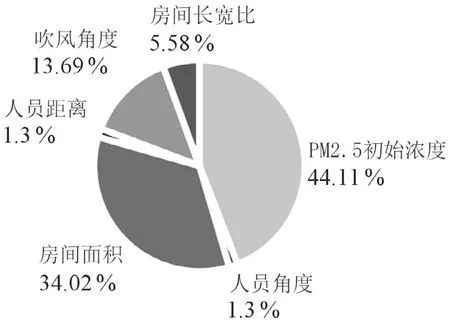
图6 影响因子贡献率
在该运行模式下,PM2.5初始浓度和房间面积的贡献率之和为78.13 %,影响显著,在使用空气净化器时应着重考虑PM2.5初始浓度和房间面积的影响。
4.3.1 固定房间尺寸和PM2.5初始浓度
在空气净化器的实际使用过程中,房间尺寸一般是固定的,当PM2.5初始浓度再确定时,其影响因子贡献率如图7所示。
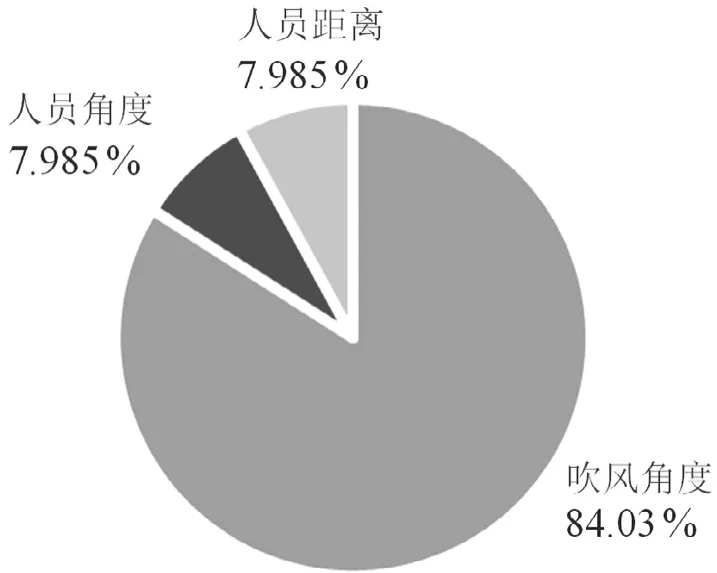
图7 固定PM2.5初始浓度各影响因子贡献率
在该运行模式下,固定PM2.5初始浓度时,其中吹风角度的贡献率由最初的13.69 %增加到84.03 %,其对PM2.5净化时间的影响程度变大,故在使用空气净化器时应着重考虑吹风角度不同而带来的气流组织的影响。
通过以上分析可得,空气净化器在送风仰角35 °、最大风速模式下,当房间尺寸和PM2.5初始浓度固定时,影响因子吹风角度对PM2.5净化时间影响程度显著,根据得到的PM2.5净化时间预测模型,其与吹风角度呈负相关,故在使用空气净化器的过程中应适当的增大吹风角度,减少PM2.5净化时间。
4.4 室内净化不均匀性分析
根据得到的预测模型,为了分析室内空气净化的不均匀性,需要对室内进行区域划分,其区域划分如图8所示(以房间面积72 m2、房间长宽比2为例)。
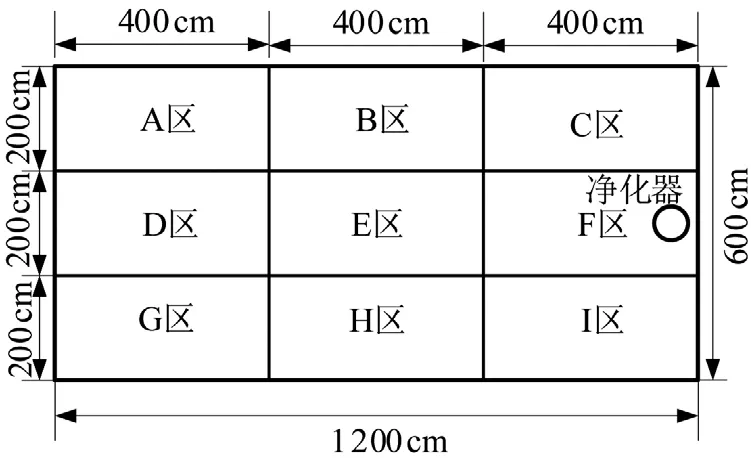
图8 房间区域划分
由于PM2.5初始浓度对PM2.5净化时间的影响程度最大,故需要探究其对室内净化不均匀性的影响。选取吹风角度为90°,PM2.5初始浓度为50、100、150 μg/m3,利用预测模型对每个区域正中心位置进行计算,得到每个区域下的净化时间,其结果如表9所示。

表9 各区域净化时间
本文类比温度和流场的不均匀系数[13],引入净化时间不均匀系数的概念,表示净化器净化的不均匀程度,将室内净化时间的标准差作为净化时间不均匀系数,其计算公式如(3)、(4)所示:

式中:
N—净化时间不均匀系数;
n—房间区域个数;
ti--第i个区域的净化时间。
根据式(3)~(4)可计算出不同PM2.5初始浓度下房间的净化时间不均匀系数,如表10所示(其不均匀系数越接近于0表示净化器对室内净化越均匀):
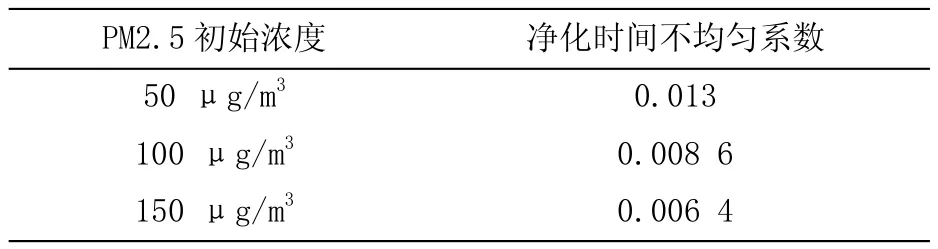
表10 房间净化时间不均匀系数
根据表10可知,在该模式下空气净化器对室内净化总体较为均匀。净化时间不均匀系数随PM2.5初始浓度的变化关系,如图9所示。
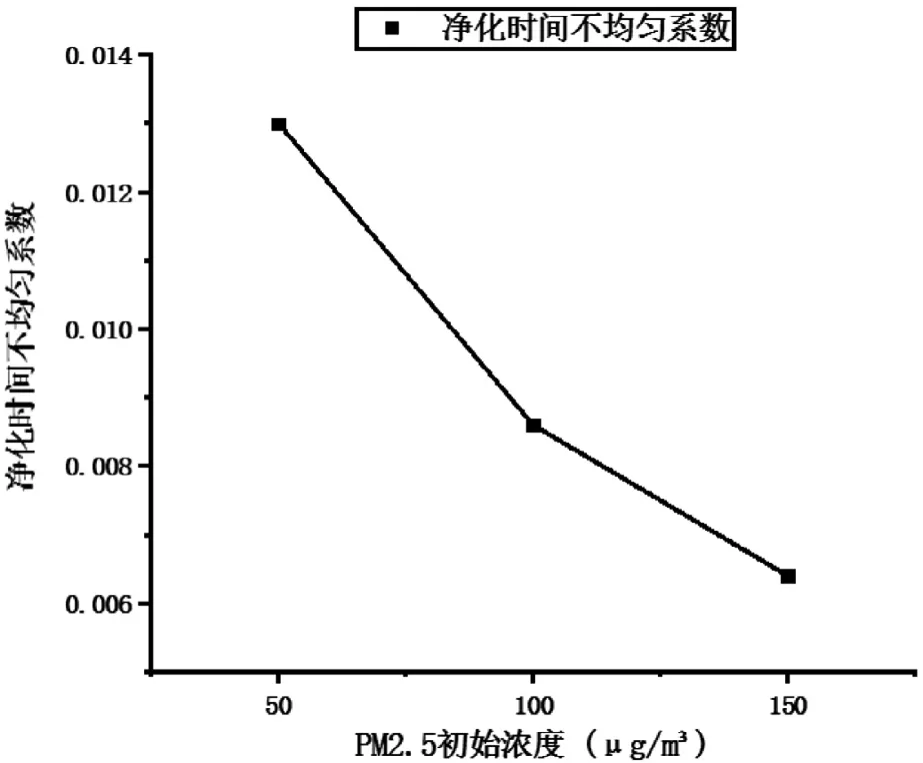
图9 净化时间不均匀系数与PM2.5初始浓度变化关系
由图9可以看出,当PM2.5初始浓度升高时,净化时间不均匀系数不断减小,其平均下降率为29.72 %。因此虽然室内空气净化总体较为均匀,但是PM2.5初始浓度对室内净化不均匀性具有较大的相对影响。
5 结论
1)通过SPSS软件对模拟数据进行回归分析,得到了空气净化器在送风仰角35°、最大风速模式下PM2.5净化时间预测模型,其中PM2.5净化时间与各影响因子之间呈线性关系关系,与人员距离、人员角度、PM2.5初始浓度、房间面积呈正相关,与吹风角度呈负相关;
2)通过影响因子贡献率分析可得,PM2.5初始浓度和房间面积的贡献率之和为78.13%,影响程度显著;在房间尺寸和PM2.5初始浓度固定时,吹风角度的贡献率由最初的13.69 %增加到84.03 %,其对PM2.5净化时间的影响程度变大,故在使用空气净化器的过程中尽可能加大吹风角度,减少PM2.5净化时间;
3)空气净化器对室内净化总体较为均匀,但是随着PM2.5初始浓度的升高,净化时间不均匀系数的平均下降率为29.72 %,故PM2.5初始浓度对室内净化不均匀性具有较大的相对影响。

