耕地质量评价缺失数据填充方法研究

陈宇，周悟，胡月明，2，3，4，5，6*，谢健文，2，3，4，6

（1.华南农业大学资源环境学院，广州 510642；2.广东省土地信息工程技术研究中心，广州 510642；3.广东省土地利用与整治重点实验室，广州 510642；4.自然资源部建设用地再开发重点实验室，广州 510642；5.青海大学农牧学院，西宁 810016；6.青海-广东自然资源监测与评价联合重点实验室，西宁 810016）

耕地是一种特定的土地，是人类活动的产物，是人类开垦之后用于种植农作物并经常进行耕耘的土地[1]。它是人类所需食物的主要源泉，是农业生产发展的主要物质基础，而耕地关乎粮食安全，粮食安全关乎国家发展与社会稳定[2]。耕地质量评价可准确评估耕地生产力与适宜性，是耕地保护、开发、政策完善等的重要前提[3]。

耕地质量评价数据是对耕地质量产生影响的指标数据集，而耕地质量评价缺失数据即是数据集中部分遗漏、未采集、已知错误的数据。耕地质量评价数据量大、类型众多，在数据获取、输入、传输过程中，存在因人员操作不当、机器故障等原因导致的数据错误与缺失的情况，而数据的错误也是数据缺失的表现形式，进而直接影响数据分析与挖掘，使得评价结果不准确、数据利用不充分[4]。而目前对于缺失数据填充方法已有相关研究，尤其插值法、最近邻填充、回归模型、期望最大化法、多重填充等方法应用相对广泛，但这些方法都存在明显的不足。空间插值法在不同区域不同数据中的最优表现有明显差异，如克里格插值、反距离加权两种方法在不同研究中表现出各自最优，但空间插值法存在方法的选择和结论的不确定性问题[5-7]；最近邻填充法是简单高效且相对高精度的填充算法，但面对不同数据集难以有稳定的填充效果，并且存在K 值难以度量的问题[8-10]；回归模型法填充局限性较大，对于数据之间的相关性要求极高，即需要数据存在必然的因果关系，并且根据数据关系构建模型费时费力，修改也极其不易[11-13]；期望最大化法是一种迭代优化过程，执行简单且稳定，逐步寻找最优解，但该算法适用于大样本，且数据集应服从正态分布[9-10，14]；多重填充法是对每个数据缺失值生成多个预测值，与上述方法不同的是该算法表现了数据集原有的不确定性，其随机性强，但运算过程复杂，精度相对较低[15]。

数据的填充能弥补数据自身的缺失或满足应用的需求，如仪器设备测量问题、操作员录入问题、分析问题等会使得数据结果与真实值存在较大差异，最终严重影响耕地质量评价结果[16]。某些数据的直接测量极其复杂或耗时耗力，甚至无法实现，因而需要采用数据填充法，如刘菲等[14]利用相关性因子对森林地林木平均胸径的填充，就是间接运用数据之间的关联性得到所需的数据。目前耕地数据库日益增加，数据规范性、完整性不足的问题愈发突出，导致数据的缺失填充愈发重要；同时对耕地调查评价愈发频繁，评价指标不断丰富，新增指标数据的获取也成为主要问题。

目前数据缺失已是不可避免的现实，而对耕地质量评价数据而言，数据的完整才是耕地质量评价的基础，由于耕地数据的采样极其复杂耗时，所以对于耕地质量评价数据的缺失填充研究迫在眉睫。当前耕地质量评价缺失数据填充没有得到系统地研究，现有的研究基本上只对耕地土壤成分缺失数据进行空间插值填充，为了科学评价耕地质量，保证土地政策和制度的有效推行，必须对当前方法进行合理利用与改进，提出耕地质量评价缺失数据填充方法，提高耕地质量评价结果的精确性和可信度。针对目前耕地质量评价数据缺失现状，本研究对耕地缺失数据的填充方法进行探讨，旨在提高耕地质量评价缺失数据的填充精度，从而完善耕地质量评价数据体系，为今后耕地质量评价等相关研究提供的理论依据，并对填充算法的应用提供更多思路与可能。

1 材料与方法

1.1 研究区概况及数据来源

1.1.1 研究区概况

从化区地处广东省中部、广州市东北部，位于113°17′～114°04′E、23°22′～23°56′N，全区总面积1 984.2 km2，2019 年末人口64.17 万。属于亚热带季风气候，年平均气温21.2 ℃，降水充足，河道纵横，水资源丰富。从化区处于珠江三角洲到粤北山区过渡地带，地势自北向南倾斜，东北高，西南低，地形呈阶梯状。2019 年农村人口占比54.89%，而基本农田面积为174.9 km2，占全区面积不足10%。从化区地理位置、耕地及采样点分布如图1所示。

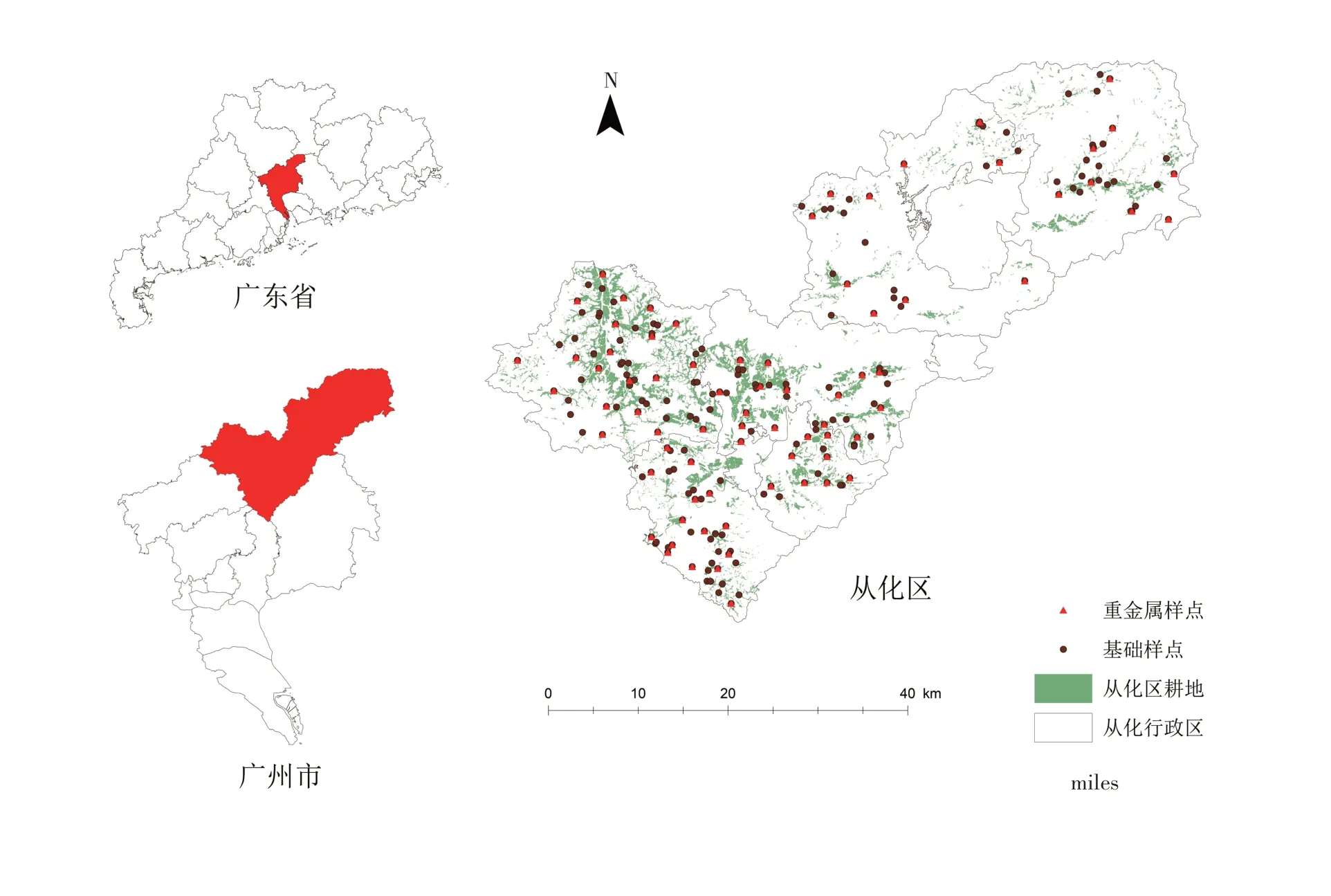
图1 从化区地理位置、耕地及样点分布图Figure 1 Geographical location,cultivated land and samples distribution of Conghua District

1.1.2 数据来源

本研究数据主要来源于广东省/广州市统计年鉴、第二次全国土壤调查、广州市基本农田调查、数据挖掘及问卷调查等。根据常用的评价指标发现[17-18]，土壤条件对耕地质量影响最大，而地形、气候虽然在小区域变化不大，但也是影响耕地质量的重要因子。本研究主要选取从化区基本农田数据、土壤重金属数据（76 个样点）、样点基础数据（204 个样点）等，将其划分为地类地形、土壤条件、气候条件3 个方面（表1），共32 个指标，5 888 条耕地质量评价数据，这些数据充分体现了从化区耕地质量的现状，为耕地质量评价奠定了基础。

表1 耕地质量评价指标Table 1 Cultivated land quality evaluation index

1.2 方法与设计

缺失数据填充方法从应用对象上主要分为两大类型，即空间性和非空间性。空间性方法是充分考虑到数据本身存在空间关联性，从而利用自身空间关联特征来通过已知数据对缺失数据进行填充的方法；而非空间性数据之间不存在任何地理关联性，只能寻找与其他数据内部的关联性，利用其关联性对未知数据进行预测填充[17]。而对于耕地质量评价数据而言，其自身的复杂多样性决定了单一方法无法解决，因此本研究在缺失数据填充方法基础上进行改进后对耕地质量评价缺失数据进行填充，并与传统方法进行精度比较。

1.2.1 空间相关性分析

空间自相关分析是检验具有空间属性的要素是否对相邻空间点属性值产生影响，所以空间相关性分析必须对其属性的空间位置和属性值进行统计。目前对空间相关性分析的方法较多，最常用的是Moran′sI指数，当I＞0 时，为正相关；I=0 时不相关；I＜0为负相关。具体计算见公式（1）[19]：

式中：xi和xj分别为i和j所在位置的属性值；xˉ为该元素属性平均值；Wij为权重。

1.2.2 填充方法

缺失数据填充方法研究已近百年，方法在不断被提出与完善，目前已提出的方法有回归模型填充、期望最大化填充（Expectation maximization，EM）、多重填充（Multiple imputation，MI）、K 最邻近填充（K-nearest neigbor，KNN）、空间插值、神经网络、随机森林等，本研究选取常用的几种缺失数据填充方法进行简单介绍并提出改进方法。

（1）常用填充方法

回归模型填充是通过对自变量与因变量之间的关系进行建模预测[5-7]。该方法对于数据之间的相关性要求极高，即需要数据存在必然的因果关系。因此主要用于分析结果数据预测，多用于时间序列预测法。

KNN 填充是利用欧氏距离度量与当前数据最相似的K条记录，然后用这K条记录在当前属性出现频率最高的值进行填充或者利用这K条记录对缺失位置的属性利用距离的归一化进行加权填充[20-22]。该方法多用于空间样点数据的填充，与常用空间插值反距离权重插值原理相同，该插值方法常应用于土壤数据、气候数据的填充，不同之处在于前者是对已知点缺失值的填充，后者是对未知点数据的预测[23-24]。

多重填充方法是对每个数据缺失值生成多个预测值，呈现缺失数据的不确定性；每个值都用来填充数据集中的缺失值，产生若干个完整数据集合；再利用相同的方法对多个数据集进行分析，筛选出最优解[15]。

期望最大化法是一种迭代算法，由两步组成：第一步是求出期望，第二步则是将随机参数进行极大化。先给随机变量一个初始值，求出模型中各个参数的估计值，然后再利用新估计出的模型对该随机变量进行估计，如此反复迭代，直至模型收敛为止[9-10，14]。

（2）四象最近邻填充

四象最近邻填充是在KNN 填充的基础上进行改进，由于KNN 法是直接筛选出最近的K个对象，有可能会存在K个对象都趋向于一方的现象，导致最终的填充结果有较大偏差，所以针对该方法的不足进行改进，提出四象最近邻填充方法[23]。四象最近邻填充方法是针对某个对象属性缺失值，在数据样本中寻找该对象每个象限中最邻近的n个对象，并利用其对应属性进行反距离加权运算，最终结果为该对象缺失值的预测值。该方法既弥补了KNN 的不足，也避免了K值选择的困难。具体过程如下：

①距离度量的确定：计算出所有耕地数据对象的属性距离，用于衡量两两之间的影响程度。本研究采用目前最常用的距离度量算法——欧式距离。

式中：dab为对象a和对象b之间的度量距离，m；xia表示第a个对象的第i维坐标，m；xib表示第b个对象的第i维坐标，m；i代表对象数据维度（本研究耕地数据为二维）；a和b代表某个数据对象。

②邻近筛选：对缺失数据对象点周边其他对象进行逐一象限筛选，对存在对象的每个象限选择n（n≤3）个对象用来填充缺失数据，n过大会导致距离太远，从而关联性降低，对于周边对象少的n取值为1，保证数据具有较高的关联性。

③权重分配：采用距离权重反比，根据缺失对象与样本点对象的距离进行加权度量，一般取值权重与距离平方成反比。具体计算表达式见公式（3）：

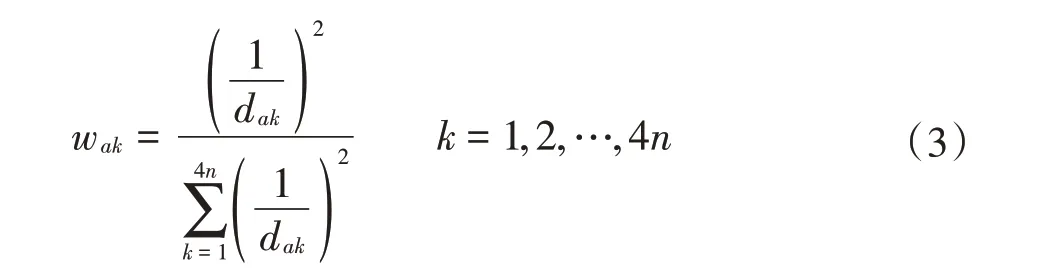
式中：wak为对象k对对象a的影响权重系数；dak为对象a和对象k之间的度量距离，m；k为缺失数据对象筛选出的第k个对象。

④缺失填充：根据缺失对象筛选出的样本对象对应属性值与权重系数计算缺失填充值。存在的特殊分类数据先将其转换为数值数据，直接选取重复率最高的进行填充。具体计算表达式见公式（4）：

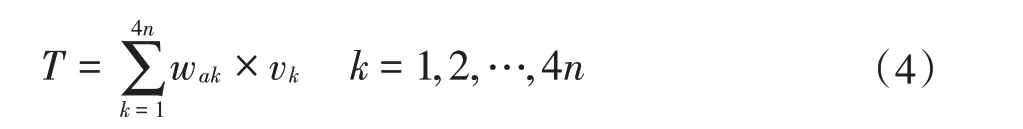
式中：T为缺失填充值；vk是第k个对象对应的属性值。

（3）相似聚集填充

相似聚集填充是将数据集划分为完整数据集和缺失数据集，通过对完整数据集内部数据自身相似关联性进行分析，通过不断迭代运算计算出数据对象间的相似性，最终利用缺失数据集中已知数据和对象相似性结果预测缺失数据集中缺失值。该方法具体步骤如下：

①数值归一化：由于耕地数据类型众多、数据量大，数据会因为属性值范围不一、文本数据、离散数据等原因，导致数据不同属性产生影响的不平衡性，所以需要将所有数据属性值归到相同数值范围内，将文本数据转换为数值数据，使所有属性影响相同。为简化归一结果，一般都选择[0，1]。数值归一化过程具体计算见公式（5）、（6）：

式中：数据集U=｛C1，C2，…，Cn｝，Umax和Umin是表示该属性数据集的最大值和最小值；Di为归一化处理后该属性中第i个属性值。

②相似度度量：计算完整数据集中对象之间的相似度，连续变量相似度计算见公式（7），离散变量相同为1，否则为0；构建相似度矩阵S。再通过构建吸引度矩阵X和归属度矩阵G（初始值为0）不断迭代直到聚集中心不变后停止，确定最终对象相似度矩阵[25]。

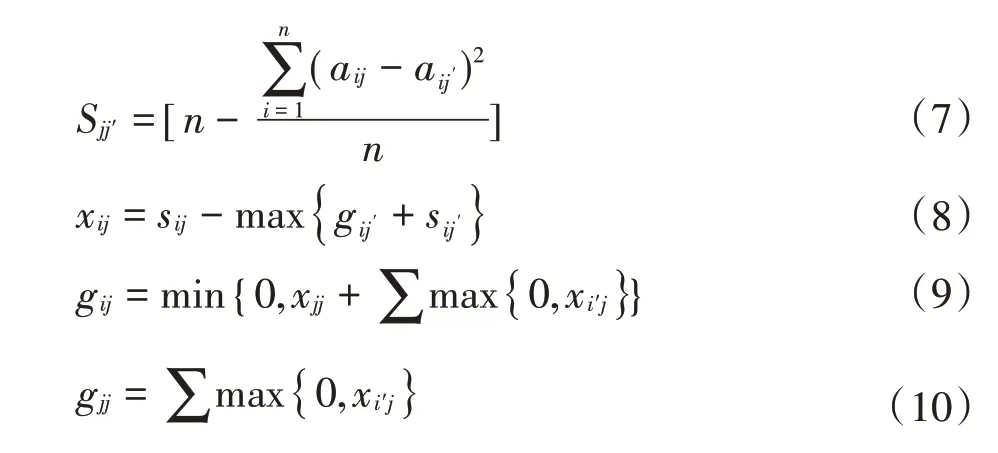
式中：aij为对象j的第i个属性的值；sij为第i和第j的对象之间的相似度；xij为第i和j的对象之间的吸引度；gij为第i和j的对象之间的归属度；i′和j′均表示非i和非j；当gjj+xjj＞0 时，迭代停止，此时与对象相似度最高的为该对象的聚集中心。

③缺失值填充：选择与缺失值对象最高相似度的k个对象作为参考值，如果其中对象也存在对应缺失值，即向下寻找下一个相似度最接近的对象。权重确定方法选择距离权重反比，具体计算同公式（2）；再通过权重和已知样品数值计算缺失值，计算式同公式（3）；对离散数据选择重复率最高的作为预测值。

1.2.3 实验设计

由于耕地数据覆盖面广、类型众多、结果复杂、数据量大、数据采集周期长等原因，对耕地质量评价缺失数据的研究较少，本研究在原有填充算法不足的前提下，提出四象最近邻和相似聚集填充方法较以往填充方法的优势。提出的两种方法是针对耕地质量评价数据结构特征，具有针对性，所以该方法在本研究的适用性较好。为验证其方法的精度并与其他填充方法比较，利用Python 3.7和SPSS 26进行数据处理和精度计算，具体过程如下。

（1）缺失处理：为验证数据填充方法的精度，选取真实完整的数据进行实验。首先使用正态分布对数据异常值进行剔除，避免数据填充过程中数据异常值影响过大，导致填充精度过低。利用空间相关性和空间分布图分析将数据集划分为空间数据集和非空间数据集；再对空间数据集中数据除去坐标数据外随机删除1%、5%、10%、15%、20%数据信息，用于模拟缺失数据集，采用四象最近邻填充方法和其余传统填充方法进行填充；对非空间数据集中随机选取5%、10%、15%、20%、25%属性因素，在其中随机删除部分属性信息，模拟缺失数据集，采用相似聚集填充方法和其余传统填充方法进行填充。

（2）精度检验：由于数据对方法的适应能力不同，为了避免偶然性，每次试验都得出不同的精度，一般取多次结果的精度平均值对模型方法精度进行估计，本研究取10 次计算结果的平均值为最终精度。精度采用预测值与真实值相关系数计算，具体见公式（11）：

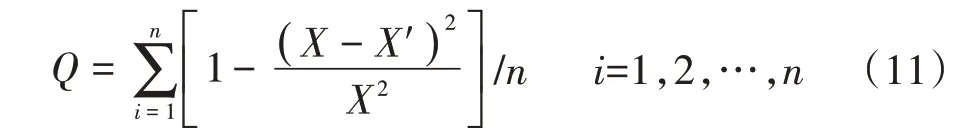
式中：X为真实值；X′为预测值；n为填充个数；Q为填充精度。

2 结果与讨论

2.1 数据统计结果

由于采集的数据会存在少量异常值，需对所有数据进行正态分布检验，本研究取置信区间为，将置信区间外的属性值划为异常值，数据检验结果（表2）表明，32 组属性数据基本符合正态分布，异常值比例均小于3.5%，平均异常值比例仅为1.2%。

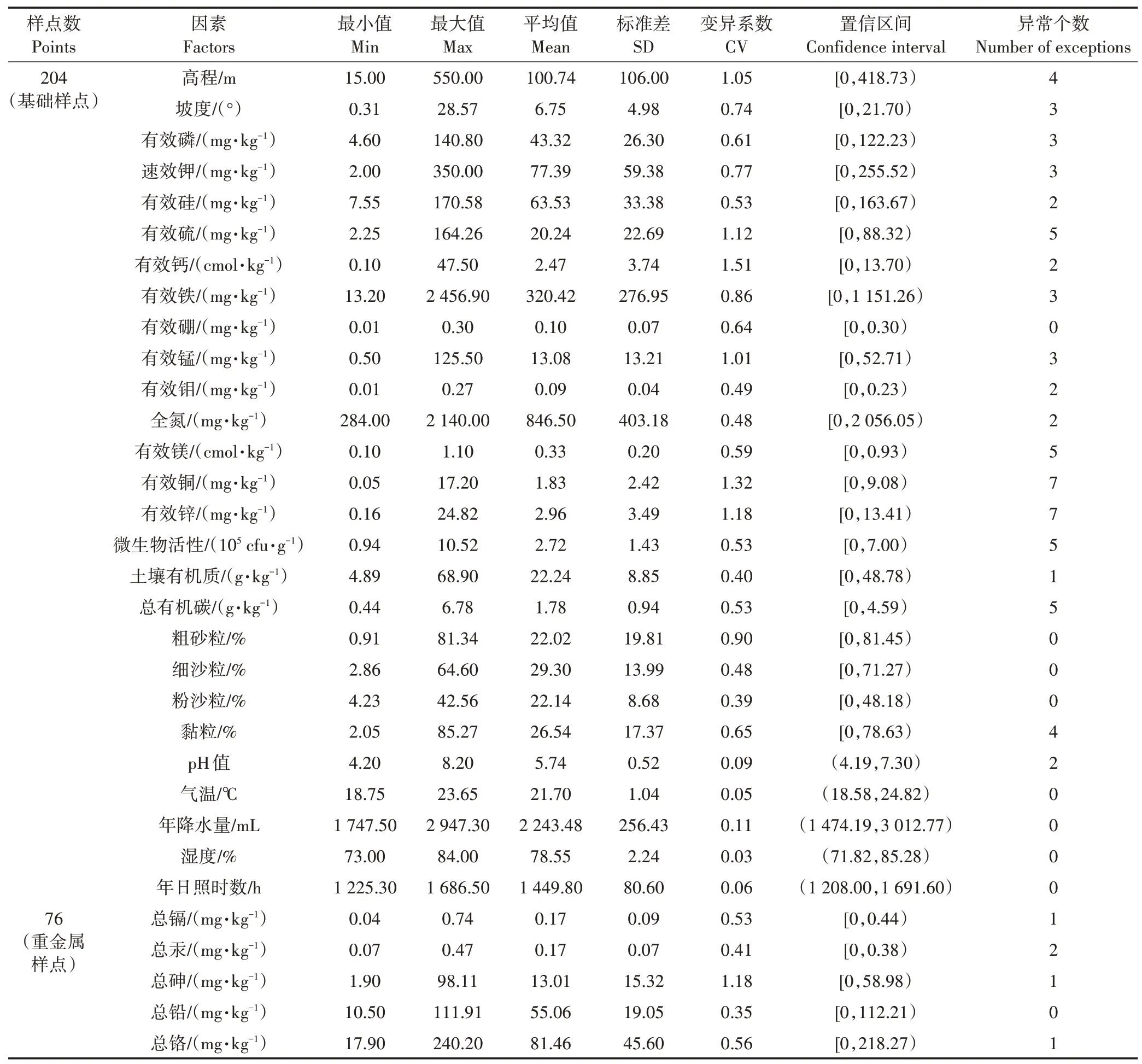
表2 从化区数据统计结果Table 2 Statistical results of Conghua District

2.2 空间相关性分析

利用ArcMap10.2 的空间自相关（Moran′sI）工具对32 组属性数据进行空间相关性检验，Moran′sI指数取值范围为[-0.261 9，0.652 1]，其中具有空间正相关的因素有高程、气温等25 个，具有空间负相关的因素有全氮、粉砂粒等7 个，具体相关性统计结果见表3。

表3 Moran′s I指数统计结果Table 3 Statistical results of Moran′s I index

虽然空间自相关分析较为客观，但为避免偶然性，本研究再利用ArcMap10.2 生成空间分布图，进一步分析数据是否具有聚集相关性[26]，部分空间分布图如图2 所示。

由图2 可以看出：从化区西南部海拔低、东北部海拔较高，具有明显的空间分布差异性；pH 值基本呈现西南部偏低、东部较高、北部居中，也具有明显的空间分布差异性；而全氮含量分布不存在明显的规律和特征；微生物含量呈现与海拔高度相反的趋势，西南部含量高，东北部含量低，具有显著的空间分布差异性。而气候条件中气温与高程分布特征基本相似，东北部山区气温偏低，西南部平原气温偏高；降水及湿度与地形特征具有较大关联性，降水量相对较高的地区分布在东北部山区南坡和西南地区。数据空间分布结果分析与空间自相关分析整体基本一致，根据最终分析结果将32 组数据集分为空间性数据和非空间性数据。

图2 高程、pH值、全氮、微生物含量空间分布图Figure 2 Elevation，pH value，total nitrogen and microbial content spatial distribution map

2.3 空间性数据填充精度评价

根据空间相关性分析得出耕地质量评价数据中的空间性数据，如高程、气温、有效锌等25 组数据，并对上述空间性数据采用回归模型法、KNN 法、期望最大化填充法、多重填充算法及四象最近邻填充法进行缺失填充，并计算不同填充方法不同缺失率下的填充精度（表4）。

从表4 可以得出，所有填充方法的填充精度均随着缺失率的上升逐渐降低，空间性数据中填充算法的整体精度表现为：四象最近邻填充＞KNN 填充＞期望最大化填充＞多重填充＞回归模型填充。四象最近邻填充算法的数据填充精度最高，在1.0%缺失率时填充精度高达92.6%；而KNN 算法在缺失率较低时，精度略低于四象最近邻填充算法，随着缺失率的不断提高，两种填充方法的精度逐渐趋于接近，主要原因是缺失率较高时，四象最近邻方法筛选各象限邻近点愈发靠远，寻找较远点导致关联性较低从而降低了填充精度。其他三种算法中期望最大化法精度相对较高，并且随着缺失率的提高精度降幅较为平缓；多重填充法在缺失率为1.0%时精度超过80%，而随着缺失率上升精度急剧下降；回归模型填充算法的精度普遍较低，在缺失率15%以下填充精度趋于稳定，而缺失率为20%时精度快速下滑。期望最大化法填充、多重填充和回归模型填充三种方法的精度相对较低可能是由于数据具有空间相关性，而这几种方法并没有对数据内部关联性进行分析，而只是运用数据值进行分析预测。

表4 不同缺失率下空间性数据各填充方法的填充精度比较（%）Table 4 Comparison of filling accuracy of different filling methods for spatial data with different missing rate（%）

综上所述，对于耕地质量评价空间性数据，本研究提出的四象最近邻填充算法在精度上相对突出并稳定，整体上优于其他方法。

2.4 非空间性数据填充精度评价

在耕地质量评价数据中，非空间性数据包括全氮、粉砂粒等7组因素，对该数据类型采取非空间性填充方法进行数据缺失填充，采用回归模型填充、多重填充、期望最大化法填充、相似聚集填充，对非空间性缺失数据进行不同缺失率下的精度计算，结果见表5。

由表5 可知：随着数据缺失率的提高，四种数据填充算法的精度都有所降低。而在这些算法中，相似聚集填充算法精度最高，在缺失率为5%～10%时，数据填充精度超过90%，主要原因是该方法集聚关联因素而避免了不同类型因素之间的相互影响。并且该算法在缺失率25%以下时，算法的精度均平稳下降，而期望最大化法填充、多重填充和回归模型填充在缺失率达到15%时精度降幅明显加快，而多重填充和回归模型填充算法在整体上的填充精度较低，即使在缺失率为5%时的精度也仅为80%左右，所以相似聚集填充算法比较稳定，且在缺失率较高时仍然能保持较好的填充精度。综上所述，相似聚集填充算法对本研究中耕地质量评价非空间关联性数据缺失填充具有优势，在精度上明显优于其他填充算法，集中表现了其精度高、稳定性强的特点。

表5 不同缺失率下非空间性数据各填充方法的填充精度比较（%）Table 5 Comparison of filling accuracy of different filling methods for non-spatial data with different missing rate（%）

3 结论

本研究以广州市从化区耕地质量评价数据为样本数据集，采用多种数据缺失填充方法进行分析，对数据进行空间相关性分析，并对缺失数据进行填补，结论如下：

（1）从化区耕地质量评价数据基本服从正态分布，异常数据较少，32 组数据中有25 组具有空间自相关性。

（2）对空间关联性数据填充精度最高的方法是四象最近邻算法，在缺失率20%以下时精度均高达80%，精度随缺失率增大而降低，其次为KNN 算法、期望最大化法、多重填充法、回归模型法。

（3）对非空间关联性数据填充精度最高的是相似聚集填充法，在缺失率25%以下时可保持80%以上的高精度，其次为期望最大化法、多重填充法、回归模型法。

（4）本研究提出的四象最近邻算法和相似聚集填充算法不仅在相同缺失率情况下精度更高，同时缺失率阈值范围更广，说明其方法的实用性更强。

综上，本研究提出的四象最近邻填充方法和相似聚集填充方法对耕地质量评价缺失数据填充的精度较其他方法有较大提升，并且更加适用于耕地领域。下一步将进行不同研究区的验证研究，来证实本研究提出方法的实用性和可靠性。