凸轮轴轴颈砂带抛光工艺研究

秦祖安 李鑫 黄正忠 张森华 陈小华

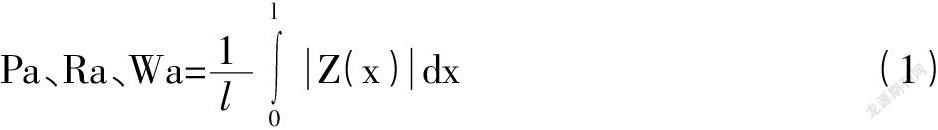
摘要：分析了凸轮轴轴颈在砂带抛光成形下的各粗糙度参数间的相互关联性;并验证了不同抛光参数对轴颈表面粗糙度的影响，为凸轮轴的表面粗糙度控制和抛光工艺参数设定提供了生产指导。

Abstract： Research on the interconnectness between camshaft journal roughness parameter which was get by belt polishing， verify the effect to the journal surfaceness caused by different polish parameter， provide guidance for roughness control and polish parameter setting.

關键词：凸轮轴;表面粗糙度;抛光;工艺参数

Key words： camshaft;surface roughness;polishing;process parameter

中图分类号：U464.136                                     文献标识码：A                                文章编号：1674-957X（2021）01-0089-03

0  引言

众所周知，发动机是汽车的心脏，而凸轮轴是发动机的核心零部件之一。配气系统的摩擦损失是发动机内耗的第三大“功臣”，占发动机摩擦损失量的7～10%。其中，活塞组件的摩擦损失居首，曲轴系统次之。凸轮轴在配气系统里质量最大，属于主动轴带动其他零件运动。因此凸轮轴减少摩擦损失技术成为提高发动机机械效率和降低油耗的重要指标，要达到减磨的效果，控制好凸轮轴摩擦副的表面粗糙度至关重要。目前，表面抛光是改善零件表面粗糙度的最直接的方法。本文针对凸轮轴轴颈表面粗糙度进行了砂带抛光试验，分析了不同抛光条件对轴颈表面粗糙度的影响关系，为凸轮轴轴颈的表面质量控制和抛光工艺参数提供了生产指导。

1  常用的表面粗糙度参数：Ra、Rz、Rmr定义

凸轮轴轴颈粗糙度一般要求为Ra0.1～Ra0.8，或者Rz1～Rz6;部分对轴颈粗糙度要求较高的主机厂，会增加Rmr（c）的要求。

1.1 粗糙度轮廓算术平均值Ra

在GB/T 3505中定义，Ra为在一个取样长度内纵坐标值Z（x）绝对值的算术平均值[1]，计算公式为：

1.2 轮廓最大高度Rz

在GB/T 3505中定义，Rz定义为在一个取样长度内，最大轮廓峰高与最大轮廓谷深之和[1]，如图1所示。

1.3 轮廓支承长度率Rmr（c）

在GB/T 3505中定义，定义为在给定水平截面高度c上轮廓的实体材料长度Ml（c）与评定长度的比率[1]，如图2所示。

2  砂带抛光成形的各粗糙度参数间的相互关联性

2.1 砂带抛光下成形的表面粗糙度Ra与Rz的对应关系

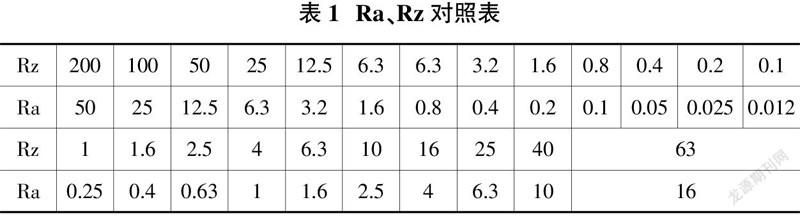
在《机械设计手册》中，针对Ra、Rz一般有如表1对应关系[2]。

凸轮轴的凸轮和轴颈的表面粗糙度一般要求Ra0.1～ Ra0.8。当粗糙度为Ra0.4～Ra0.8时，一般采用高速磨削的加工方式，当粗糙度为Ra0.1～Ra0.4时，一般采用先磨削再进行砂带抛光的工艺方法;由表1可知在Ra0.8以内时有如下关系：

Rz=8Ra（2）

该对应关系在实际运用中，存在一定偏差;图3为凸轮轴轴颈抛光实际检测的Ra及Rz数据。

对数据中Ra、Rz进行线性拟合，得到以下回归方程：

Rz=9.4591Ra+0.1103;     R2=0.9097（3）

将以上回归进行简化：

Rz =10.5Ra;     R2=0.8976（4）

由此可计算出如表2所示对照表。

2.2 砂带抛光下成形的表面粗糙度Ra与Rmr（DEPTH-0.25）的对应关系

Rmr（c）为轮廓支承长度率，它反应的是零件的耐磨性，Rmr（c）值越大，轴颈越耐磨损。从定义上，Rmr与Ra没有直接关联，实际运用中，能直观的发现Ra越小，Rmr（c）的值会越大。

下面针对国内某汽油发动机凸轮轴轴径的粗糙度要求Rmr（DEPTH-0.25），分析Ra与Rmr（DEPTH-0.25）的对应关系;根据试验过程实际检测的数据，做出Rmr（DEPTH-0.25）与Ra的散点图（图4）。

对数据进行线性拟合，得到以下回归方程：

Rmr（DEPTH-0.25）=-4.3633Ra+1.2141;R2=0.9402（5）

根据以上回归，计算出如表3所示对照表。

从以上数据看，当Ra达到0.05时，Rmr （DEPTH-0.25）为99.59% ，当Ra在0.25时，Rmr12.33%;在实际工艺应用中，Rmr（DEPTH-0.25）要达到99%以上在工艺实现上比较困难。而外圆磨床磨削后的产品粗糙度Ra0.35的情况下，Rmr（DEPTH-0.25）已经达到15%;磨削后的产品粗糙度Ra0.24时，Rmr（DEPTH-0.25）已经达到28%。所以Rmr（DEPTH-0.25）在不同工艺方法下，其相对Ra的关系会有变化，但基本是与Ra呈正相关的;而当Rmr （DEPTH-0.25）要求≥50%时，一般都需要采用抛光等工艺进一步提升表面粗糙度质量。

3  不同抛光参数对轴颈表面粗糙度的影响

凸轮轴轴颈抛光的粗糙度，与产品抛光前的粗糙度、抛光时工件转速、抛光压力、抛光带目数、抛光振荡频率、振荡幅度、抛光时间、抛光介质等参数均有关系;以某型号发动机凸轮轴为例;轴颈表面粗糙度要求：Rmr（DEPTH-0.25）80%min，为了保证抛光后轴颈直径变化量稳定在0.002mm左右，我们选定1200目抛光带，在0.5Mpa抛光压力下验证不同抛光参数能达到的Rmr（DEPTH-0.25）水平。

对影响Rmr（DEPTH-0.25）的相关参数进行最佳子集分析，得到表4。

其中模型3的 Cp和S最小，同时R2在74.4;意味着Rmr（DEPTH-0.25）与抛光时的工件转速、抛光时间相关，对Rmr（DEPTH-0.25）与工件转速和抛光时间进行线性回归：

Rmr（DEPTH-0.25）=0.472+0.000134S+0.00446t（6）

其中，S為抛光转速，t为抛光时间。（表5）

S=0.0886036   R-Sq = 74.4%   R-Sq（调整） = 72.5%

由回归方程可知，Rmr（DEPTH-0.25）与工件转速和抛光时间均为正相关，但拟合度只有74.4%;对回归方程进行残差分析（图5）。

从残差图可看出，残差和拟合值分布类似泊松分布，拟合曲线可能非线性;下面分别列出Rmr相对于工件转速和抛光时间的散点图，以观察分布规律（图6）。

由图6可看出，Rmr（DEPTH-0.25）相对工件转速基本呈对数分布;进行对数拟合得到以下回归方程：

y= 0.1317ln（x）-0.1658;R2=0.8503（7）

由图7可看出，Rmr（DEPTH-0.25）相对抛光时间基本呈对数分布，但也明显存在偏离点;进行对数拟合得到以下回归方程：

y=0.1103ln（x）+0.4893;R2=0.257（8）

由于工件转速和抛光时间的乘积正好为抛光圈数;在最佳子集分析中，模型2中变量仅有抛光圈数，但是R-Sq只有39.7%，由此推断Rmr与抛光圈数也应呈正相关，但非线性;尝试做出Rmr与抛光圈数的散点图，并做回归分析。（图8）

由图8可看出，Rmr（DEPTH-0.25）相对抛光圈数呈对数分布;并有以下回归方程：

y=0.1006ln（x）+0.2258;R2=0.9004（9）

根据数据可看出;Rmr （DEPTH-0.25）随着抛光圈数的增加成对数增长;并可计算出表6所示对应表。

综上，Rmr（DEPTH-0.25）随着抛光圈数的增加成对数增长，在抛光圈数达到300以上时，Rmr（DEPTH-0.25）达到80%;且抛光圈数继续增加，Rmr（DEPTH-0.25）会变大，但是提升效果不明显。

4  结论

①表面粗糙度轮廓Ra、Rz、Rmr（c）之间有一定的相关性;Rz与Ra呈线性正相关，Rmr（c）与Ra呈线性负相关。

②在轴颈抛光工艺中，Rmr（DEPTH-0.25）相对抛光圈数呈对数分布，在抛光圈数达到300以上时，Rmr （DEPTH-0.25）达到80%;且抛光圈数继续增加，Rmr （DEPTH-0.25）会变大，但是提升效果不明显。

参考文献：

[1]GB/T 3505，产品几何技术规范（GPS）表面结构轮廓法术语、定义及表面结构参数[S].2009.

[2]悉爱军.凸轮轴表面粗糙度光整技术研究[J].现代车用动力，2012（02）：53-56.

[3]王海龙，杨正凯，薛泽波.凸轮轴抛光机床及调整凸轮密封轴颈抛光精度方法[J].装备维修技术，2012（01）：25-28.