混合频谱共享方式下面向多信道接入的动态频谱分配算法

周 鑫，陈 勇，张 余，何攀峰

（1.陆军工程大学，江苏 南京 210007；2.国防科技大学，江苏 南京 210007）

0 引言

随着无线通信业务的飞速增长，频谱资源日益短缺。基于认知无线电技术（Cognitive Radio，CR）[1]的频谱共享策略作为一种能够提升频谱利用效率，缓解频谱资源紧缺的有效方法，近年来引起了人们广泛关注。频谱共享方式可以分为填充式（overlay）和下垫式（underlay）两种[2]。在overlay 方式下，系统只能将主用户未使用的授权信道分配给次用户[3]，而在underlay 方式下，系统可将任意授权信道分配给次用户，但次用户的发射功率需控制在给定的干扰门限之下[4-5]。

综合两种频谱共享方式的优点和不足，学者们提出了面向混合频谱共享方式的动态频谱分配策略，使系统可根据次用户的异质性和信道状态，调整频谱共享方式，最大化次用户总吞吐量[6-8]。为了减少信道切换次数和充分利用信道资源，近年来许多研究成果从单信道接入的动态频谱分配场景，扩展到了多信道接入的动态频谱分配场景。文献[9]提出了一种单次用户多信道的感知和分配策略，并通过线性规划得到了最优策略；然而，当信道特性不同时，这种方案可能不是最优的。文献[10]提出了一种分配策略，通过进行多次单信道接入的频谱分配方法，将所有可用信道分配完毕；但该算法在某些次用户达到最低传输速率需求时，会继续为其分配信道，这可能影响整个分配过程的吞吐量最大化。文献[11]以次用户吞吐量最大化为目标，考虑了次用户的最大可接入信道数，将动态频谱分配问题表述为在可用信道集内的线性整数规划问题，以较低的复杂度得到了较高的吞吐量；但该算法没有考虑次用户最大发射功率的约束条件，没有对发射功率进行优化。文献[12]提出了基于竞争深度Q 网络的动态频谱分配策略，将次用户发射功率离散化处理，以便在功率分配方面进行优化；但是该问题模型是在underlay 方式下，不需要考虑信道忙闲状态对功率分配的影响，因此不适用于混合频谱共享方式下的频谱分配问题。

本文主要讨论混合频谱共享方式下次用户可接入多个信道场景的动态频谱分配问题，并考虑受硬件和功率限制的情况下，每个次用户的总发射功率以及最大可接入信道数均存在上限。在满足信道限制和功率约束的条件下，本文算法相比文献[10]和文献[11]中的算法，能够进一步提升次用户总吞吐量。

1 系统模型

本文构建的混合频谱共享方式下多信道接入场景中，包含M个次用户收发对和N个主用户收发对。N个带宽为B的相互独立信道，分别授权给N个主用户。系统为次用户i分配信道的同时，也确定了共享方式，次用户需要根据不同共享方式下信道的传输功率限制，调整发射功率[13]。若主用户未占用信道，则可采用overlay 方式，次用户在单个信道j内的发射功率Pi,j不得超过信道j传输功率上限；若主用户占用信道，则次用户i需释放信道或降低发射功率Pi,j，以underlay 方式与主用户j共用信道。Underlay 方式下，次用户i发射功率Pi,j不得超过的同时，传输到主用户j接收机处不得超过其干扰门限。由于本文主要研究频谱分配策略，因此假设信道占用情况可基于频谱数据库实时获得[14]。其中：aj为主用户对授权信道j的占用状态，aj=1 为信道占用，aj=0 为信道空闲。次用户i同一时隙可接入多个信道，但不能超过Fi个信道，每个信道同一时隙只能分配给一个次用户，次用户i总发射功率不能超过其最大发射功率。系统共存模型示意图如图1 所示。

图1 系统共存模型

次用户i在underlay 方式下，不可对信道j内主用户产生有害干扰，即次用户i发射功率Pi,j经过信道衰落传输到主用户j接收机处，不能大于干扰门限。因此，underlay 方式下次用户i在信道j发射功率需满足：

根据系统模型和式（1），可得次用户i在信道j上的信噪比为：

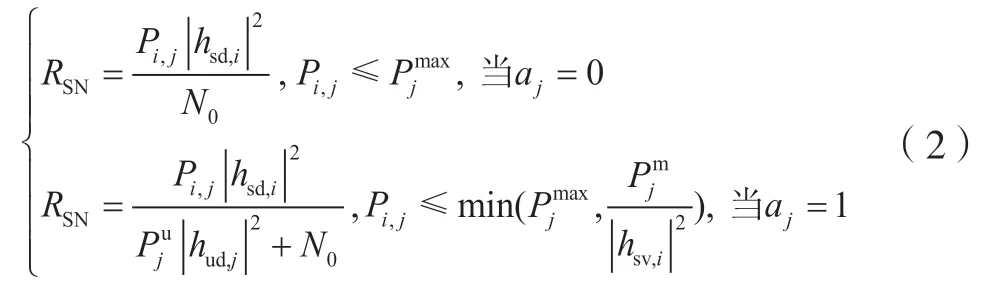
式中：N0为噪声功率；为主用户j发射功率。

2 频谱分配模型

2.1 问题描述

为了避免次用户间发生冲突，并且更有效地利用频谱资源，提升系统总吞吐量，系统需要为各次用户分配信道。由于信道占用状态、传输功率限制以及主用户发射功率均存在差异；因此，次用户在接入不同信道后信噪比会有所差异，从而影响总吞吐量。本文要讨论的问题是，如何为各次用户进行信道分配和功率分配，使各次用户在满足最低传输速率的前提下总吞吐量最大；同时次用户的发射功率需要满足单信道内的传输功率限制，也不能超过underlay 方式下的干扰门限以及次用户的最大发射功率上限，且各次用户分配的信道不超过最大可接入信道数。

2.2 约束条件

2.2.1 传输速率约束条件

在最大化总吞吐量的同时，需要保证各次用户的吞吐量满足最低传输速率需求，即：

Bf={bi,j|bi,j∈{0,1}M×N}为信道分配矩阵，当信道j分配给次用户i，bi,j=1；当信道j未分配给次用户i，bi,j=0。

2.2.2 信道约束条件

每个次用户至少分配一个信道，但受硬件条件限制，每个次用户i最多分配Fi个信道。为了防止次用户间冲突，每个信道最多分配一个次用户，即：

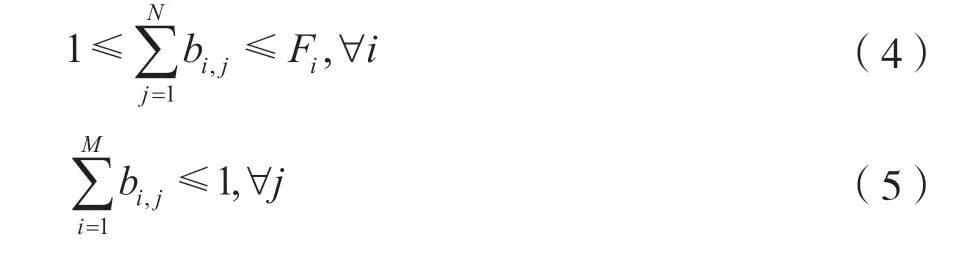
2.2.3 功率约束条件

受各信道传输功率限制，每个次用户在单个信道j内的发射功率不得超过，同时当次用户在underlay 方式下，传输到主用户接收端的功率不得超过干扰门限，且次用户i在所有信道内的发射功率之和不得超过其最大发射功率，具体可表示为：

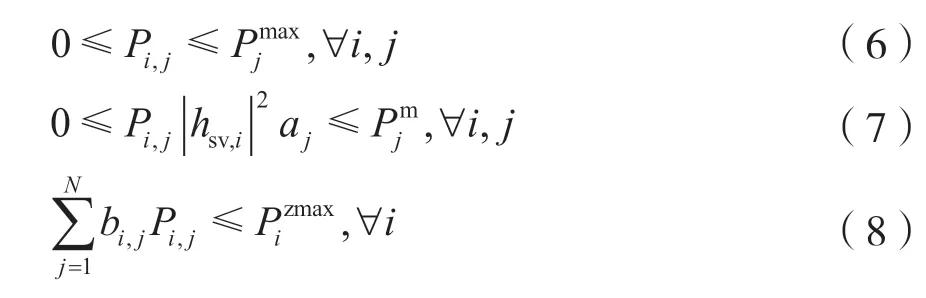
2.3 目标函数

本文的目标是在需满足传输速率、可用信道以及发射功率等约束条件下，通过优化信道分配策略和功率分配策略，最大化系统总吞吐量。根据香农公式，次用户i在信道j的吞吐量为：

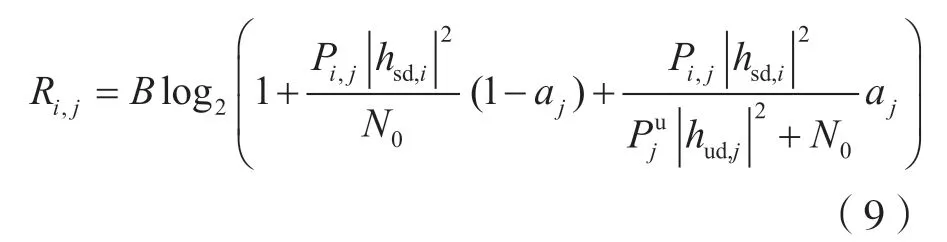
因此，本文动态频谱分配问题的目标函数为：

式中：Pf={Pi,j}M×N为功率分配矩阵；Pi,j为次用户i在信道j上分配的发射功率；C1为各次用户在所有信道内传输速率之和需满足最低传输速率需求；C2为每个次用户同一时隙可分配多个信道，但最多可接入Fi个信道；C3为每个信道同一时隙只能分配一个次用户；C4为次用户在每个信道中的发射功率不为负且不超过单信道内传输功率上限；C5为underlay 方式下，次用户在每个信道中的发射功率，传输到主用户接收机处不得超过其干扰门限；C6为每个次用户在所有信道发射功率的总和不超过自身最大发射功率；C7为信道分配矩阵中各元素的取值范围为0 或1。

3 循环迭代优化算法

3.1 算法设计

由于目标函数涉及到2 进制变量bi,j和实数变量Pi,j，因此式（10）是一个混合整数规划问题。求解式（10）的主要困难在于整数约束条件C7，如果采用直观的穷举搜索，则需要先生成M N个可能的信道分配方案，而后讨论每种方案下的功率分配策略。当信道数较大时，这显然也是不切实际的。若将整数变量松弛为连续变量，转化为含多个决策变量的非整数规划问题，则会出现仿射函数与凹函数相乘，导致目标函数无法被证明是凸函数。

本文提供一种算法，通过引入循环迭代机制，将信道分配和功率分配联合优化，可解决式（10）的混合整数规划问题。该算法先在给定发射功率的约束条件下，初始化一个功率分配策略，在第z(z≥1)次迭代的时候，令，优化信道分配矩阵Bf，得到优化后的信道分配矩阵为；接下来令，优化功率分配矩阵Pf，得到；然后令，继续第(z+1)次迭代；最终至系统总吞吐量收敛，可得近最大总吞吐量以及信道和功率近最优分配策略。

3.1.1 优化信道分配策略

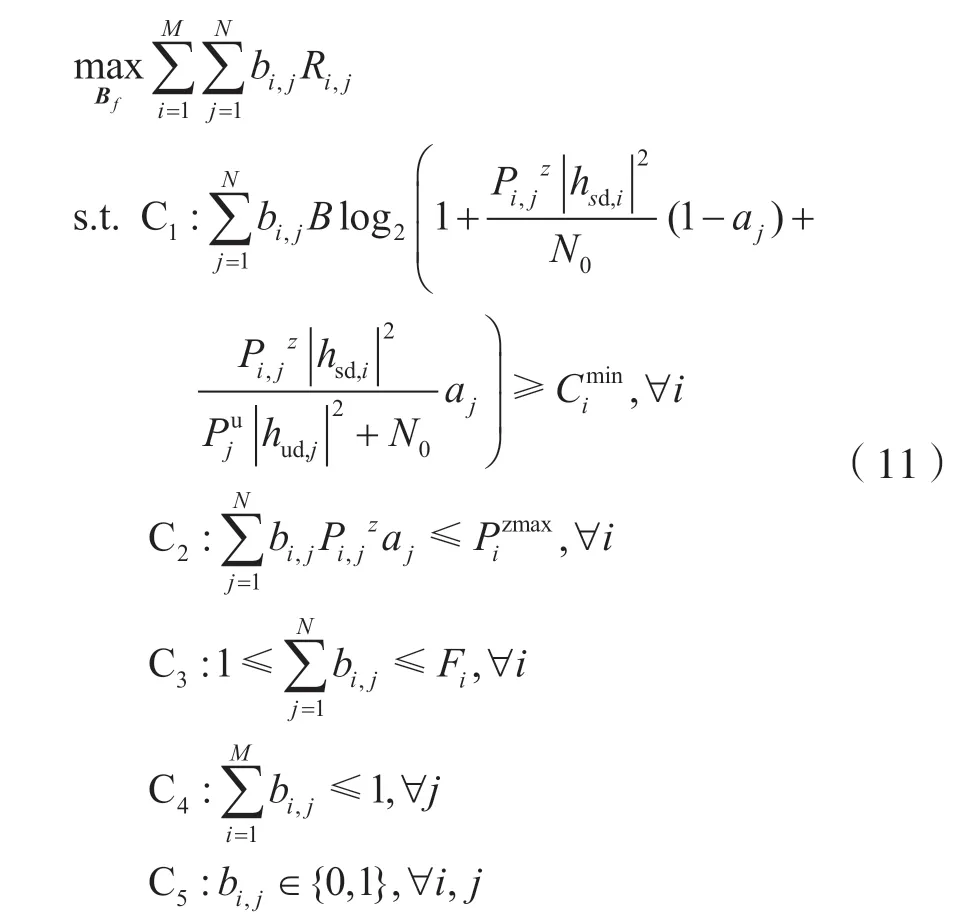
式（11）是一个关于Bf的线性函数，且约束条件均为仿射函数，因此可以证明式（11）为凸函数，则该子问题可解。

3.1.2 优化功率分配策略

当Bf=时，将Bf作为固定变量，Pf作为决策变量，原问题转化为非整数规划问题，可表述为：

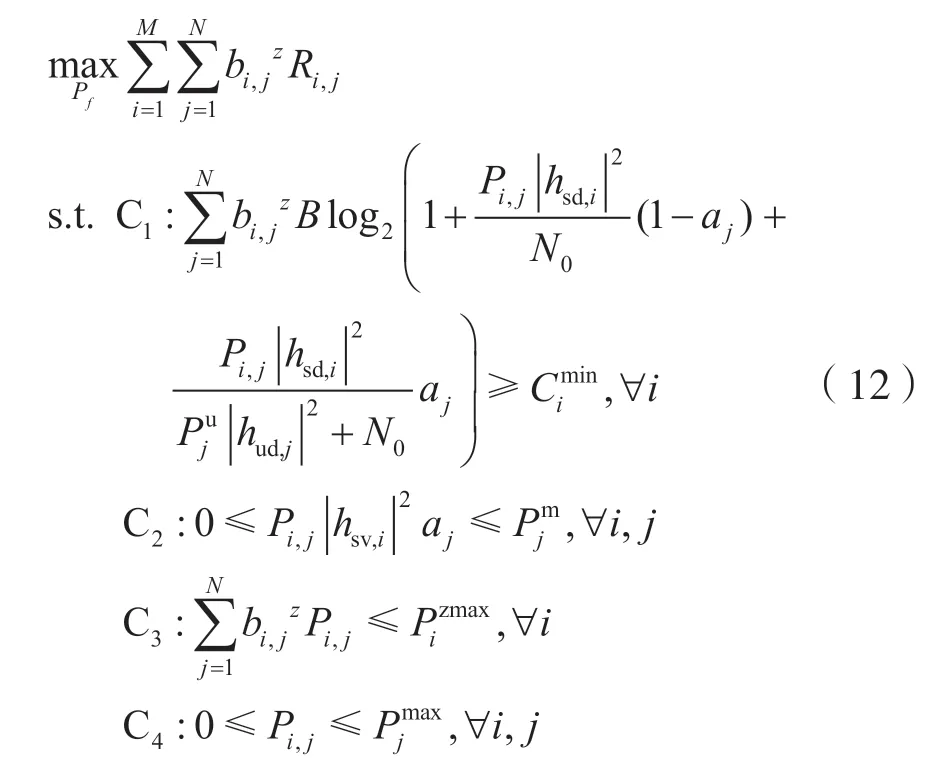
式（12）中总吞吐量为关于功率分配矩阵Pf由以下两个函数复合而成：

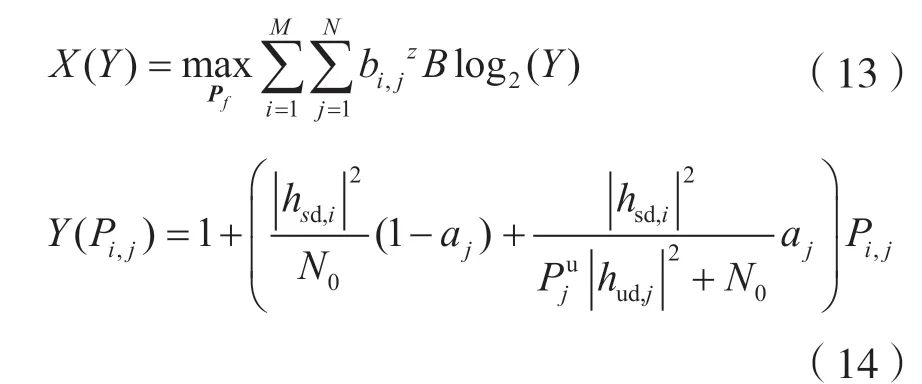
式（13）和式（14）分别为对数函数和仿射函数，且仿射函数中Pi,j的系数因此可以证明X(Y)、Y(Pi,j)均为凹函数，则-X(Y(Pi,j))为凸函数。同理式（12）的约束条件也可证明为凸函数，则该子问题可解。

3.2 算法流程

从提升次用户总吞吐量，同时满足各项约束条件角度出发，本文提出了混合频谱共享方式下基于迭代优化的动态频谱分配算法，具体流程如下：

步骤1：根据频谱数据库，获得当前时隙各授权信道的占用状态数组A={a1,a2,…,aN}，aj∈{0,1}，表示N个授权信道的占用状态。

步骤2：初始化迭代次数z=1，信道分配矩阵Bf为零矩阵，总吞吐量(z=1)=0；根据信道占用状态和各约束条件，设置一个满足条件的功率分配矩阵(z=1)，作为初始化值。

步骤3：将作为固定变量带入式（12），Bf作为决策变量，用整数规划方法，得到优化后的信道分配矩阵。

步骤4：将作为固定变量带入式（13），Pf作为决策变量，用非整数规划方法，得到优化后的功率分配矩阵和总吞吐量，更新迭代次数，z=z+1。

步骤5：判断是否满足结束条件，若≤ε（ε为给定任意小的正数）或循环次数超过30 次，则结束算法，输出信道分配矩阵、功率分配矩阵和总吞吐量；若不满足结束条件，则转至步骤3。

本文算法流程如图2 所示。

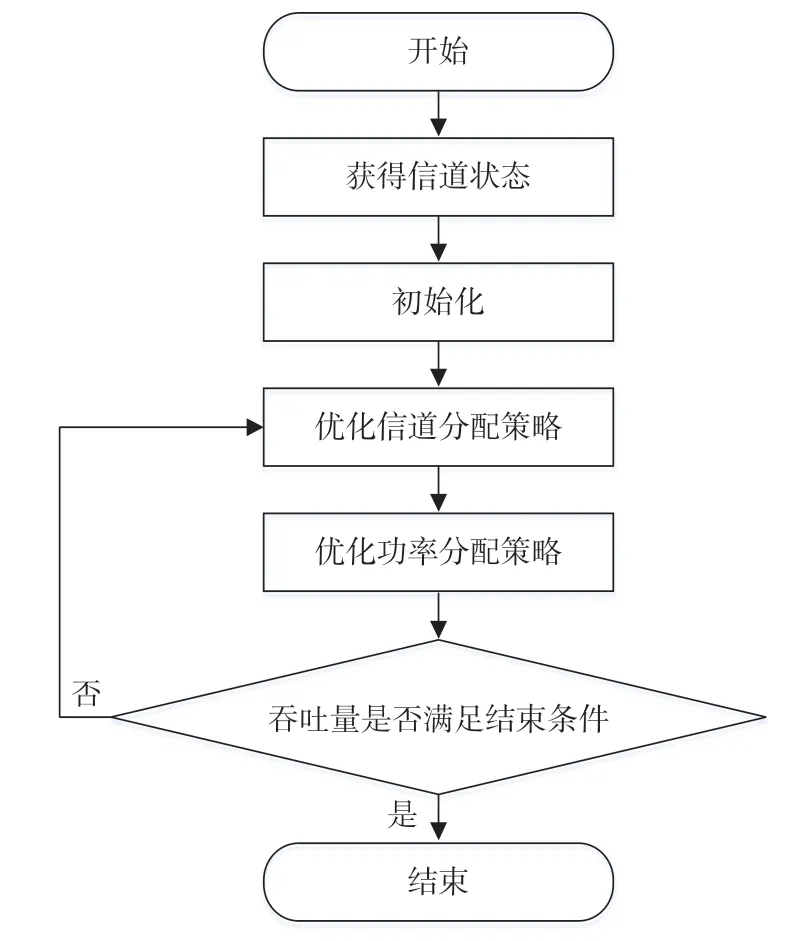
图2 本文算法流程

4 仿真结果与分析

为了验证本文算法在混合频谱共享方式下，多信道分配求解问题的性能，本节采用仿真对比方法，即通过与文献[10]、文献[11]和随机算法进行对比，分析本文算法的性能。文献[10]通过进行多次单信道接入方式的频谱分配，将所有可用信道分配完毕，并采用最大权匹配算法，确保每次单信道接入的频谱分配过程吞吐量最大。文献[11]算法中次用户以各信道传输功率上限作为发射功率，而后将信道分配问题表述为一个线性规划问题进行求解。随机算法为依次随机一个选择信道，并随机确定共享方式分配给一个次用户，当某一次用户达到最大发射功率或可接入信道上限后，停止为该用户分配信道；当所有次用户分配完毕或所有信道分配完毕，分配过程结束。

仿真实验以次用户总吞吐量为目标，仿真长度为100 个时隙，比较每个时隙总吞吐量的平均值，同时采用蒙特卡洛实验策略，进行100 次相互独立实验并取其平均值为最后实验结果。系统仿真参数设置如表1 所示，次用户仿真参数设置如表2 所示。

表1 系统仿真参数

表2 次用户仿真参数

主用户和信道由于数量较多，且仿真中讨论了吞吐量随信道个数的变化趋势，所以其参数采用在区间内随机选择的方式产生。主用户在授权信道内占用和空闲状态符合两状态马尔科夫随机过程[15]。从区间(0,5]中随机选择15 对实数，分别作为各主用户参数λ和μ；从区间[0.8,1.2]中随机选择15 个实数作为各主用户发射功率，单位w；从区间[0.7,1]中随机选择15 个实数作为underlay 方式下信道传输功率限制，单位w；从区间[0.9,1.1]中随机选择15 个实数作为各授权信道内的发射功率上限，单位w。

图3 是本文算法、文献[10]算法、文献[11]算法和随机算法在不同授权信道数下的次用户总吞吐量对比。从图3 中可以看出，前3 种算法相比随机算法，吞吐量有较大提升。随着信道数增加，本文算法吞吐量逐渐优于文献[10]算法和文献[11]算法。这是因为当信道较少时，各次用户最大发射功率和可接入信道数均未达到上限，而授权信道数是影响总吞吐量的主要因素，所以4 种算法的吞吐量随信道数增加而提升。前3 种算法均能够根据信道占用情况选择最佳信道和共享方式，并以相应共享方式下的最大发射功率进行通信，充分利用信道资源，因此前3 种算法的吞吐量近似。当信道数增加至9 个时，部分次用户发射功率达到上限，文献[10]算法和文献[11]算法中，这部分次用户无法继续分配信道，只能根据新增信道的情况，将已接入的信噪比较低信道调整为信噪比较高信道，使吞吐量获得少量提升，至所有次用户调整至最佳信道。而本文算法中，发射功率达到上限的次用户可以降低已使用信道中的发射功率，继续使用新增的信道资源，使吞吐量获得较大提升。当信道数增至15 个时，本文算法所有次用户可接入信道达到饱和，系统无法为次用户增加分配信道的数量，但仍可以为次用户分配信噪比更高的信道，替换信噪比较低的信道，至所有次用户均分配到最佳信道。

图3 不同授权信道数下的次用户总吞吐量对比

图4、图5、图6、图7 分别是本文算法、文献[10]算法和文献[11]算法，在授权信道数为6 和15 时的信道分配策略和功率分配策略。从图4、图5、图6、图7 中可以看出，当授权信道数为6 时，3 种算法均能充分利用信道资源，本文算法与文献[11]算法的策略一致，而文献[10]算法相对更加兼顾公平性，因此策略稍有不同。当信道数为15 时，文献[10]算法和文献[11]算法中次用户虽然可接入信道数未达上限，但受次用户发射功率的限制，无法使用剩余信道资源；而本文算法可以继续优化功率分配策略，充分利用15个信道进行通信。

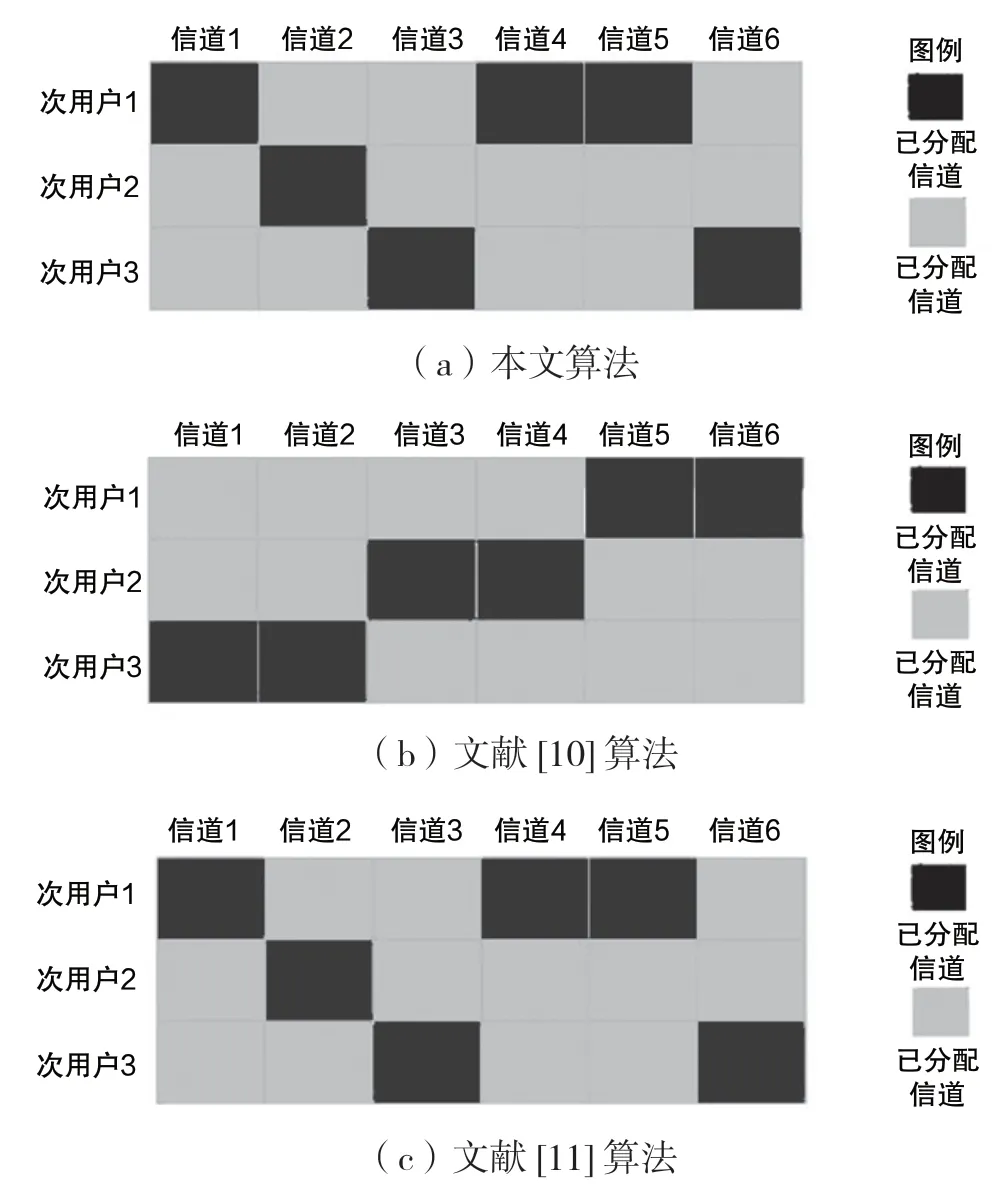
图4 6 信道时信道分配策略对比

图6 15 信道时信道分配策略对比

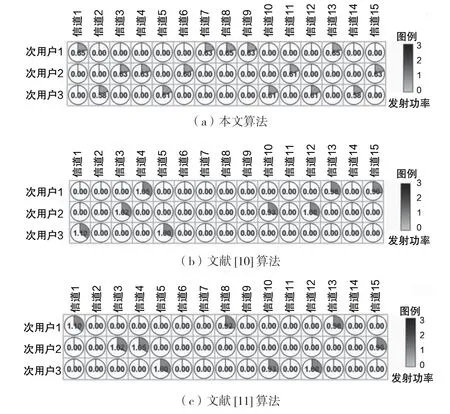
图7 15 信道时功率分配策略对比

图8 是本文算法与文献[10]算法、文献[11]算法和随机算法，在不同最大可接入信道数下的次用户总吞吐量对比。从图8 中可以看出，前3 种算法相比随机算法，吞吐量有较大提升。随着信道数增加，本文算法吞吐量优于文献[10]算法和文献[11]算法。这是因为当次用户最大可接入信道数较低时，可接入信道数是影响总吞吐量的主要因素，所以4 种算法的吞吐量随最大可接入信道数增加而提升，前3 种算法均能够根据信道占用情况选择最优信道和最佳发射功率通信，因此前3 种算法的吞吐量近似。当最大可接入信道数增加至4 个时，部分次用户发射功率先达到上限，文献[10]算法和文献[11]算法中，这部分次用户最大受发射功率限制，无法继续分配信道，系统吞吐量不在增加。而本文算法中，发射功率达到上限的次用户可以降低已使用信道中的发射功率，继续使用更多的信道资源，使吞吐量获得提升。当最大可接入信道数增加至5 个时，本文算法中次用户可接入信道数均达到上限，因此系统吞吐量不再增加。

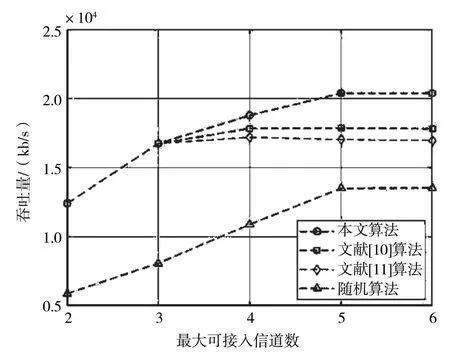
图8 不同最大可接入信道数下的次用户总吞吐量对比

图9 是次用户最大发射功率分别为4 w、3 w、2 w 情况下，本文算法总吞吐量随次用户数的变化趋势。当次用户数较少时，信道资源相对充足，因此最大发射功率越大，总吞吐量越大。次用户在单个信道上的发射功率最高为1 w 左右，因此最大发射功率为4 w的情况下，满功率发射需要约4 个信道（未达到最大可接入信道数5）。当用户数超过4 时，系统所需信道数约为16，超过现有授权信道数15，因此总吞吐量不在增加。同理，当最大发射功率分别为3 和2 时，则次用户数分别达到5 和7 时，总吞吐量收敛，此时吞吐量主要受授权信道数影响，因此3 种情况收敛值接近。

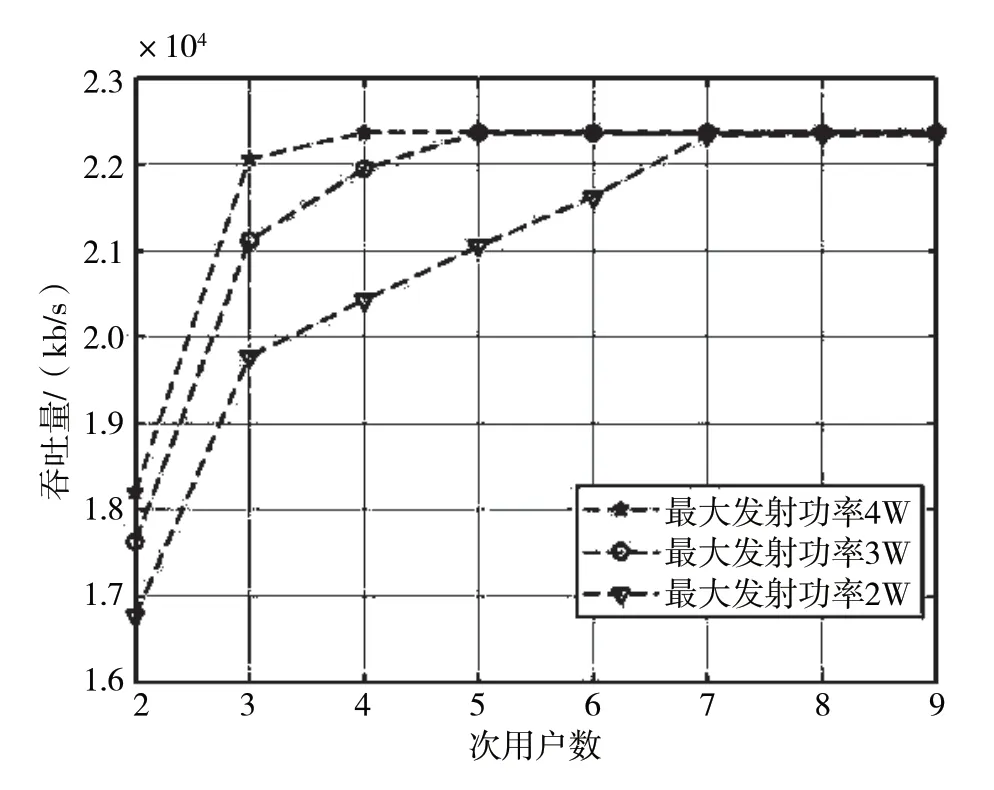
图9 本文算法次用户数与吞吐量关系

5 结语

本文构建了混合频谱共享方式下面向多信道接入的动态频谱分配问题模型，同时考虑了异质次用户最大发射功率、最大可接入信道数、最低传输速率需求以及信道传输功率限制等约束条件，并提出了一种基于信道分配与功率分配策略循环迭代优化算法。通过两个决策变量的交替迭代优化，将难以求解的非凸问题转化为两个凸函数的形式，得到了问题的局部最优解甚至全局最优解。仿真结果表明，本文算法能对信道和功率进行联合优化，有效提升次用户通信总吞吐量，尤其是在次用户和信道数量较多的情况下，本文算法能比最大权匹配算法、线性规划算法和随机算法等现有算法获得更优的性能。但由于本文算法使用多次迭代，也存在复杂度较高的问题。