基于灰色系统理论的高速铁路桥梁施工控制
白 浩,冯志勇
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
随着高速铁路运营速度大幅度提高,高速列车对桥梁结构的动力作用更加明显,梁体出现的挠度会使整个桥梁结构承受更大的冲击力,这就要求桥梁的成桥线形精度更高,桥面更加平顺[1].在大跨度高速铁路桥梁的建设过程中,悬臂浇筑法是目前主流的施工方法,因而在桥梁施工过程中,对主梁线形的预测调整、掌握主梁应力控制截面应力值的变化规律是整个施工控制的主要任务,以此保证桥梁结构安全可靠[2].
本文采用灰色系统理论对悬臂浇筑梁段的预拱度进行优化,进而确定下一个梁段的立模标高,最终使梁段精确合龙,成桥后梁体线形达到设计要求.同时对关键截面的应力进行实时监控与预测,用实测值、理论值、预测值三者相互校核,确保了梁体结构在施工过程中的安全性,为今后大跨度高速铁路连续梁桥及连续刚构桥的施工建设提供参考.
1 灰色系统理论GM(1,1)模型
信息匮乏用“黑色”表示,信息完整用“白色”表示,信息缺失或不充分则用“灰色”表示,信息不完全的系统,称为灰色系统或简称灰系统(Grey System)[3].灰色系统理论是由我国邓聚龙教授于1982年首次提出,该理论能以现有较少的数据作为原始数据序列,对原始数据进行加工处理,建立GM(1,1)预测模型,以此来表明系统未来的发展变化情况,具有所需样本少、精度高、控制方便等优点[4].把高速铁路桥梁的施工过程看作1个系统,运用灰色理论,则可以预测梁体的线形走向以及应力变化规律,使得桥梁施工过程中的未知因素及难度大大减少.
GM(1,1)模型建立原理如下:
设x(0)为n元序列,有
x(0)=[x(0)(1),x(0)(2),…,x(0)(n)].
(1)

(2)
则得到累加生成数据列x(1),即
x(1)=[x(1)(1),x(1)(2),…,x(1)(n)],
(3)
式中:x(1)为x(0)的累加生成数(Accumulated Generating Operation,AGO).

(4)
则Z(1)=[z(1)(2),z(1)(3),…,z(1)(n)],
(5)
式中:z(1)为x(1)的紧邻均值生成序列.
以上序列x(0)、x(1)具有微分内涵,则称为灰微分序列[5].
各时刻数据满足关系式
(6)
其中:
yN=[x(0)(2),x(0)(3),…,x(0)(n)]T,
(7)
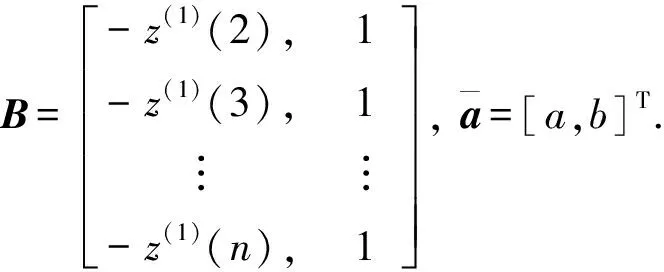
(8)
式(6)的分量形式为
x(0)(k)+az(1)(k)=b,(k=2,3,…,n).
(9)
建立方程
(10)
式(10)是标量方程且称之为预测模型的影子方程.
通过求解影子方程式(10),得到GM(1,1)模型的近似响应式为
(11)

(12)
2 施工监控实例
2.1 工程概况
本桥位于新建铁路赣州至深圳客运专线潼湖特大桥374#~377#墩,为无砟轨道(64+116+64)m双线预应力混凝土连续梁桥.边跨跨径64 m,中跨跨径116 m,起点桩号DK383+813.115,终点桩号DK384+058.615,桥梁全长245.5 m(包含374#墩和377#墩支座中心线延长至两侧梁端部的0.75 m),设计行车时速为350 km/h.桥梁防护墙内侧净宽9.0 m,桥梁宽12.6 m,建筑总宽12.9 m.截面最低梁高为5.2 m,分别位于边跨支架现浇段及中跨合龙段.截面最高处梁高为8.9 m,位于375#墩和376#墩墩顶.主梁梁高按曲线半径为418.10 m的圆曲线缓和变化.箱梁顶板宽12.6 m,底板宽7.0 m,横截面布置形式为单箱单室直腹板截面.顶板厚46.5 m,腹板厚变化由4个阶段组成,分别为50、60、85、105 cm,底板厚由跨中的50 cm按圆曲线变化至中支点梁根部的99.8 cm,中支点局部加厚至150 cm.以本桥为工程背景,基于GM(1,1)模型进行连续梁桥施工控制实践研究.
2.2 施工及监控方案
2.2.1 现场施工状况
本桥主梁的施工方法采用悬臂浇筑法,以375#墩和376#墩为支点将主梁划分为2个T构,沿T构纵向总共划分为2×15个悬臂浇筑梁段,即从墩顶向边跨和中跨分别划分为6×3.00 m、7×3.50 m、2×4.00 m 15个块段,如图1所示. 0#块段及边跨直线段均采用支架现浇的方式,长度分别为13 m和5.75 m. 全桥有1个中跨合龙段和2个边跨合拢段,长度均为2.0 m,且均采用吊篮现浇.
本文运用Midas/Civil 2019有限元软件建模,施工监控采用梁单元建立单梁计算模型,共有79个单元,80个节点,边界条件按施工现场实际采用的方法进行模拟,即先刚构后连续,有限元模型如图2所示.

图1 施工阶段划分及测点布置(单位:cm)

图2 有限元模型
2.2.2 主梁高程测试截面及测点布置
主梁在悬臂浇筑施工过程中,梁段立模标高的合理确定是关系到主梁的线形是否平顺、是否符合设计的一个重要问题[7].在确定立模标高时,如果充分考虑了各种因素带来的不利影响,并且采用合适的控制方法将这些负面影响降到最低,则最终梁体线形走向较为良好;如果不利因素带来的误差得不到有效控制,则原始误差将会一直累积,导致最终实际成桥线形与设计成桥线形有较大的偏差.
本次线形监控是在每一个梁段悬臂端距末端5~10 cm附近布设5个监测点,其中1个点布设在主梁中心线上,另外4个点分别对称布设在边腹板及悬臂上,如图3所示.

图3 标高测点布置(单位:cm)
2.2.3 主梁应力测试截面及测点布置
应力监控是连续梁桥施工监控的主要内容之一,它是施工过程中的安全预警系统,是对桥梁的实际受力状态进行评判和确保施工安全顺利的主要依据[8].在箱梁的关键控制截面埋设应力计,记录每个施工阶段完成后控制截面应力变化的规律,同时以当前阶段的应力值为原始数据建立模型,预测下一施工块段完成后的应力值.将预测值与理论及实测值进行比较,确保每个块段施工完成后的强度满足设计的要求,以此来平稳有序地推进整个梁体的安全施工.
根据主梁施工的内力影响线分析,全桥选择0#块及7#块末端截面,总计8个横截面作为应力控制截面并布置温度型应力传感器(可同时测量温度与应力),每个截面顶底板各布置3个,确保实测应力值的真实度及有效性,总计48个传感器,布置形式如图4所示.

图4 应力测点布置(单位:cm)
3 灰色系统理论在施工控制中的应用
3.1 立模标高确定
桥梁在悬臂施工过程中,整个主梁的挠度测量主要包括每个阶段的底板立模标高、混凝土浇筑前梁顶标高、混凝土浇筑后梁顶标高以及预应力钢筋张拉后梁顶标高,根据这些采集的实测资料与现场实际情况,对理论计算值进行调整[9],然后提供下一块段箱梁底板的立模标高,确保成桥后梁体线形走向满足设计要求.本文运用灰色系统理论,将当前块段实测的抬高值和有限元软件计算的理论预拱度的比值作为原始数据列,对下一阶段的预拱度进行调整,进而为下一阶段梁体的施工提供优化调整后的底板立模标高.
以375#墩大里程方向5#块段箱梁底板立模标高的实际运用值为例,阐明灰色模型GM(1,1)在本桥主梁施工预拱度优化调整中的应用过程,其设计标高和张拉后标高及理论预拱度如表1所示.设α=[α(1),α(2),…,α(n)]是1#~4#块梁段的理论预拱度序列值,与理论值对应的实测抬高值序列为β=[β(1),β(2),…,β(n)],则实测值与理论值的比值x(0)=[x(0)(1),x(0)(2),…,x(0)(n)]为GM(1,1)预测模型的原始数据列,其中x(0)(i)=β(i)/α(i),(i=1,2,…,n).根据灰色系统理论,可计算下一梁段的预测预拱度为
Hy=x(N+1)α(N+1).
则下一块段的立模标高[10]为
H1=Hs+Hy+Hg,
式中:H1为施工现场实际采用的底板立模标高;Hs为设计标高;Hy为优化后的预拱度值;Hg为挂篮的弹性变形值,由施工单位在现场通过加载试验确定.
根据表1中的数据,GM(1,1)模型的原始数据列为
根据前文的灰色系统理论原理,可得GM(1,1)预测模型为
经过还原生成后第5#块预拱度调整值为1.093 035,则实际预拱度是15×1.093 035=16.4 mm,另外施工现场实测得挂篮弹性变形为15 mm,则5#块段实际立模标高是H1=Hs+Hy+Hg=74.264+0.016 4+0.015=74.295 4 m,经过计算其误差不到0.002%,精确度很高.
3.2 应力值预测
应力监控是高速铁路连续梁桥施工监控必不可少的一项工作,它在主梁的施工过程中起着安全预警的作用.对桥梁结构每个阶段的受力状态进行实时反馈并确保下一阶段施工能够安全顺利地开展.主梁施工悬臂根部截面混凝土内纵向应力随着预应力张拉、支架施工或全部脱架后全部处于悬臂状态,以及体系转换等各个施工阶段的不同工况随时都在发生变化,由于该截面受力十分复杂,内应力的变化较大,是主梁混凝土内应力的关键控制截面[11].本文运用灰色系统理论,将当前块段施工后在某一截面产生的应力值作为GM(1,1)模型的原始数据序列,预测下一个现浇块段施工完成后在该截面上产生的应力值大小,以此来判别该节段施工的质量是否合格,以及保证整个桥梁结构始终处于安全状态.当实测应力值与预测应力值相差较大时,应及时停止施工并查明原因,排除相关隐患后方可继续进行下一施工阶段.
参照预拱度的分析方法,选取376#墩大里程方向1#~4#块段分别施工完成后在0#块段顶板产生的应力值为例,作为灰色模型的原始数列,预测5#块段施工完成后在0#块段顶板产生的应力值大小,以此说明灰色系统理论在连续梁桥应力监测方面的运用.相关数据如表2所示.

表2 376#墩大里程方向0#块段控制截面应力值 MPa
由表2中的数据可得灰色模型原始数据列为
根据灰色理论可得预测模型为
经过累减逆生成后,5#梁段施工完成后在0#块控制截面产生的应力预测值为6.598 MPa,而通过Midas Civil/2019有限元软件计算出的相应控制截面的理论应力值为6.456 MPa,相对误差仅为2.2%,表明该预测值的精度较高,可以起来超前预报的作用.
4 施工控制效果分析
4.1 成桥后梁体线形分析
根据灰色系统理论,为了保持预测模型的可靠性和精度,本文选择新陈代谢GM(1,1)模型,即将新获得的数据补充到原始数据列同时剔除掉最老的数据,保持数据的维度不变,然后重新建模,使灰色系统中的原始数据与实际工程始终保持联系[12].本文利用1#~4#块的实测抬高值与理论预拱度的比值作为原始数列,运用灰色模型预测5#块的预抬高值,然后在进行下一阶段的预测时,剔除1#块实测抬高值与预拱度的比值,加入5#块对应的值,依次类推,可以得到5#~15#块的预测值.全桥悬臂块段浇筑施工完成且预应力筋张拉后,可得梁体的实际走向,其与理论走向的对比如图5所示.
由图5可见:基于灰色模型修正立模标高后的实际成桥线性与理论线性走向一致,最大差值为7 mm,最小差值为1 mm;小里程边跨合龙段高程误差为2 mm,大里程边跨合龙段高程误差为3 mm,中跨合龙段高程相对误差为3 mm,满足悬臂梁段顶面高程以及合龙前两悬臂端相对高差控制项目的要求.全桥整体的实际走向之所以都高于理论走向,是因为实际测量时没有考虑混凝土的收缩徐变以及周围温度环境的影响[13],导致实际值偏高.
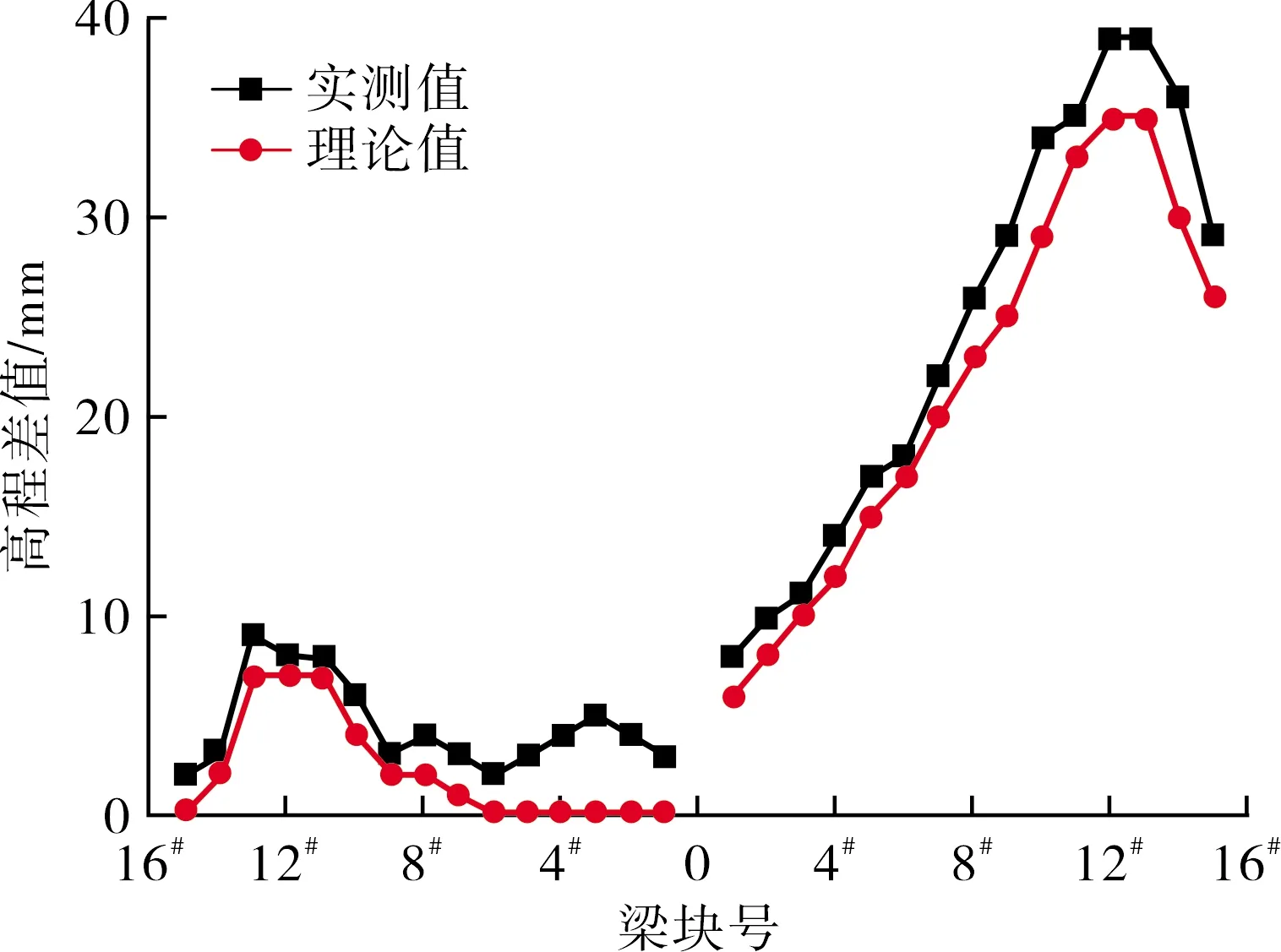
图5 梁体走向对比
4.2 应力预测结果对比分析
全桥分别在375#墩和3763#墩的0#块、7#块以及12#号块都埋设了应力计作为施工应力监控截面.由于2个T构施工具有对称性,本文只对376#墩大里程方向关键截面,即0#块应力控制截面的顶板应力控制结果进行分析.因为GM(1,1)预测模型的精度和可靠性不随原始数据数量的增加而得到提高,相反,原始数据越多,预测值与实际值的相对误差可能会更大.所以本次应力预测的模型依然采用新陈代谢GM(1,1)模型,即在模型中不断加入新的实测数据同时剔除旧的数据,保持预测模型与实际工程的关联度.376#墩大里程方向0#块应力控制截面实测应力值、预测应力值及理论应力值三者之间的对比关系如图6所示.
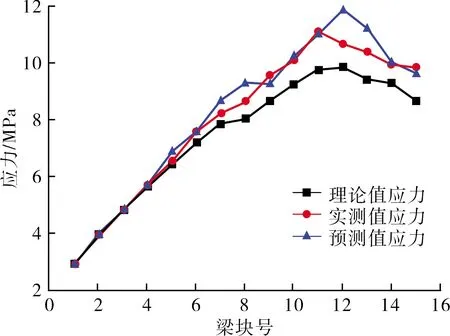
图6 理论、实测及预测应力值对比
由图6可知:实测值与理论值的平均绝对误差为0.563 MPa;预测值与实测值的平均绝对误差为0.289 MPa.控制截面上顶板的实测应力值均为压应力,且实测应力值与理论应力值的走向一致,表明该桥在整个施工过程中实际应力状态良好,结构处于始终安全状态.
5 结论
1) 本文运用灰色系统理论对新建铁路赣州至深圳客运专线潼湖特大桥374#~377#墩连续梁桥进行了施工控制.采用GM(1,1)模型对施工预拱度进行了优化调整,并对关键控制截面的应力进行了预测评估.
2) 工程实践表明,该桥引入灰色系统理论的方法后,大大减少了施工控制的难度.主梁线形在施工过程中以及合龙成桥后都处于精确且有序的控制之中,主梁线形最大偏差为7 mm,合龙段相对偏差值最大为3 mm,均符合规范要求.
3) 控制截面的应力预测值与实测值与理论值走向一致,起到了超前预测监控的效果,并且三者之间可以相互验证、相互校核,使梁体结构的真实状态一直在控制之中,保证了桥梁结构及相关作业人员的安全.综上所述,灰色系统理论在本桥的控制工作中取得了理想效果,可为以后高速铁路连续梁桥及连续刚构桥施工控制提供参考.

