数理统计技术在储层流体性质识别中的应用

魏玉梅，刘文钰，刘俊东，刘永河，窦如胜，王顺利，孟姝婳

(1.中国石油集团测井有限公司 天津分公司，天津 300280；2.中国石油天然气股份有限公司大港油田分公司 第四采油厂，天津 300280；3.中国石油集团渤海钻探工程有限公司 第一录井分公司，天津 300280)

1 引 言

储层岩性、物性、电性及含油性可以用测井资料进行表征，而电性对含油性最为敏感[1,2]，同样，电性又受岩性、物性的影响较大，也有可能会受地层水矿化度[3]及泥岩电阻率的影响。由于电阻率的影响因素较多[4]，在进行储层流体性质评价中会出现多解性[5]。针对这一难题，通过对测井资料在油水层的表征进行分析，厘清油水层敏感曲线[6]，利用数理统计技术，将能够综合反映储层流体性质特征的多种测井资料结合，建立储层分类评价的多参数图版[7]和定量判别函数，对未知类型的储层进行分类。该方法能够降低异常数据对分类结果的不良影响[8]，综合考虑多项测井参数，使分类结果更加可靠真实。

2 数理统计技术在储层流体性质识别中的应用

2.1 数理统计方法原理

本次方法研究，主要是利用数理统计方法中的均值聚类和Fisher判别分析法[9]，通过对一些样本的诸多已知性质进行分析提取、建立样本分类规则来实现对未分类样本的归类。它的几何意义是通过选择适当的投影方向，把由几个变量构成的高维空间的点群向低维空间投影，并进行适当的变换，把几个原始变量组合成一个新的变量R，使得不同类样本的R值尽可能分离开来，达到将样本归类的目的[10,11]。

根据数理统计评价原理，将能够反映储层流体性质的测井参数归类，达到对油层、油水同层、水层的定性和定量评价。

2.2 储层流体性质识别方法研究

2.2.1 选取储层流体识别参数

选取大港油田板中东断块2019～2020年已试采井的测井资料，遵循参数间应尽可能独立的原则，从测井响应参数中选取最能反映油水层特点的参数[12]：反映储层含油性的深电阻率(Rt)；反映储层邻近纯泥岩的电阻率(Rsh)；反映储层岩性的自然伽马(GR)；反映储层邻近纯砂岩和纯泥岩的自然伽马(GRmn、GRmx)；反映储层物性特征参数[13]的声波(AC)，将以上参数作为判别分析的观察值[14]。选取的特征参数，基本能消除由于岩性、物性等因素对电阻率的影响，更准确的反映真实储层流体性质。

选取有代表性的试采井14口井93个数据点(油层64个数据点、油水同层16个数据点、水层13个数据点)作为已知油层、油水同层和水层3类储层的已知样本。

为了验证选择数据的可靠性，将93个数据点进行了聚类分析，从聚类谱系图(图1)中可以看出，储层可以分为3个类别，正好符合研究中油层、油水同层、水层三类储层的划分，也证明资料对储层流体性质的划分是可靠的。

图1 聚类谱系图Fig.1 Cluster pedigree

2.2.2 数理统计技术在储层流体性质识别中的应用

1)均值聚类分析建立多参数油水解释图版

传统的双参数——声波与深电阻率油水解释图版(图2)，由于存在高电阻率水层，点子杂乱，同一区域，油层、油水同层、水层有重合的现象，无法区分。

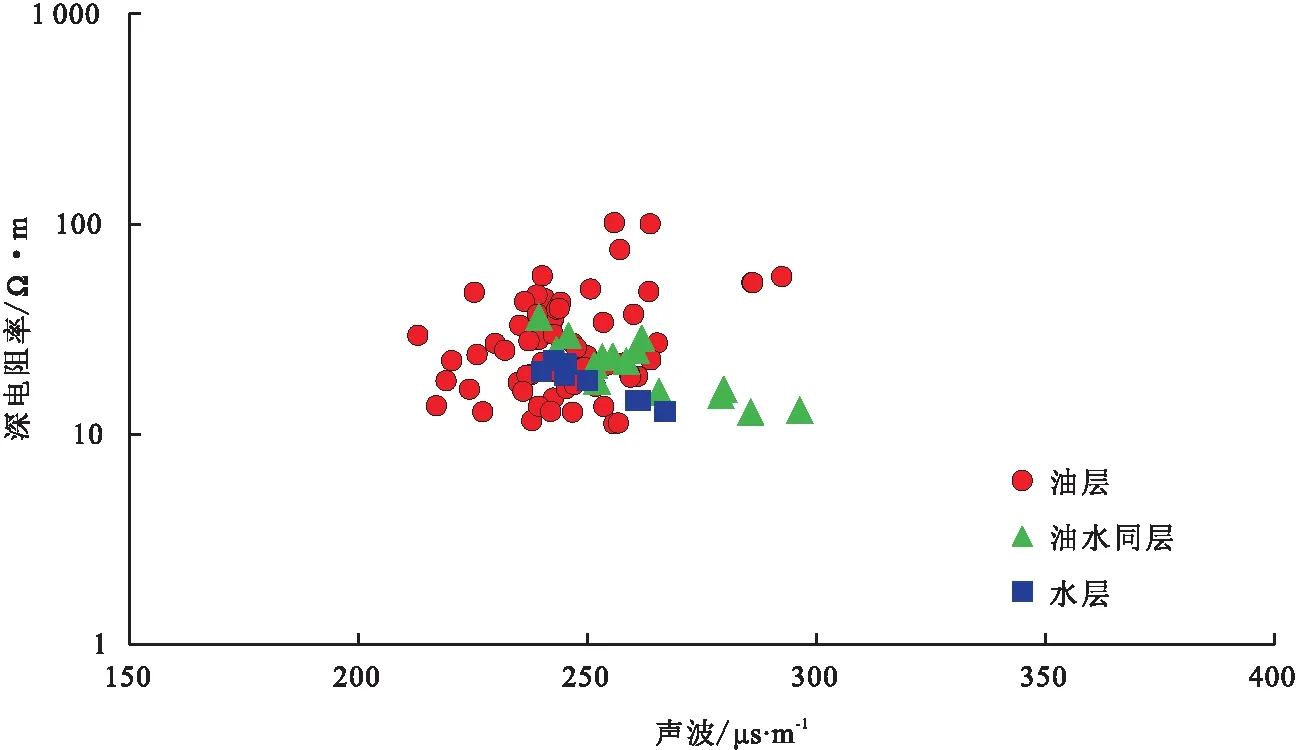
图2 双参数油水解释图版Fig.2 Oil-water interpretation chart of two-parameters

通过均值聚类分析，把每个样品作为一类，然后把最靠近的样品(即距离最小的样品)首先聚为小类，再将已聚合的小类按其类间距离再合并，不断继续下去，最后把一切子类都聚合到一个大类[15,16]。将试采井的93个数据点进行归类，建立了多参数油水解释图版，从图中看，油层、油水同层、水层能够明显的区分开(图3)[17]，与双参数图版对比，优势明显。

图3 多参数油水解释图版Fig.3 Oil-water interpretation chart of multi-parameters

同时，在图版建立之时，根据判别分析技术，对各特征参数求取判别向量，即第 1、第 2判别向量，进而计算出综合指标函数1和函数2，即公式(1)和公式(2)。

公式中：y1、y2为图3中函数1、函数2，单位是无量纲；GR为自然伽马，单位是API；GRmx为纯泥岩自然伽马，单位是API；GRmn为纯砂岩自然伽马，单位是API；Rsh为纯泥岩电阻率，单位是Ω·m；Rt为地层深电阻率，单位是Ω·m；AC为声波，单位是μs/m。

利用已知数据对图版的准确性进行验证，能够正确地对94.6 %的原数据进行分类(表1)，准确率较高。

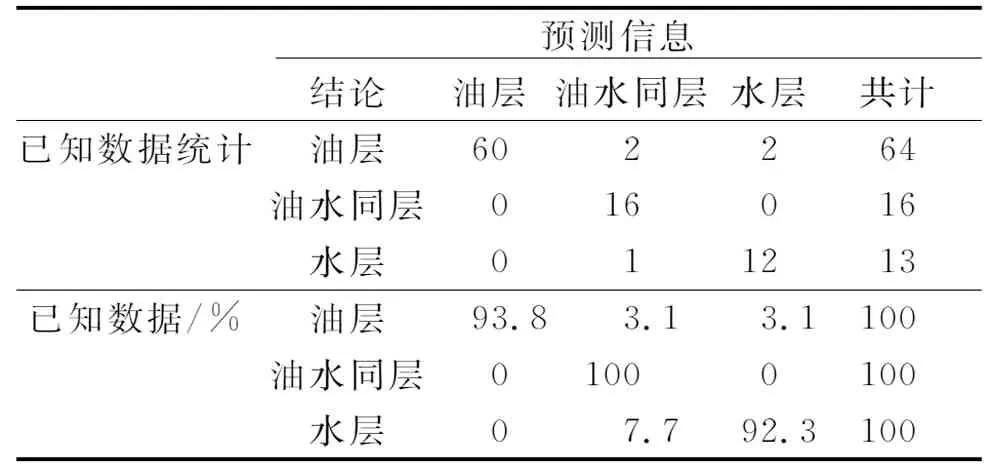
表1 分类结果Table 1 Classification results

2)Fisher判别分析法建立储层分类函数模型

另外，根据已知样品类型，运用判别分析技术，建立了油层、油水同层、水层3类层流体性质识别函数模型[18]，详见公式(3)至公式(5),实现了油水层定量评价标准[19]。

油层:

(3)

油水同层:

(4)

水层:

式中：GR′为自然伽马相对值，见公式(6)，无量纲。

最终计算的3个函数值，哪个值最大，该点就属于相应的哪一类。该方法达到对流体性质进行定量识别的目的。

3 应用效果分析

应用数理统计技术，将能够反映储层特征的多种测井资料进行融合，建立了多参数油水解释图版和定量判别技术，对板中东断块的17口井进行重新评价，解释符合率由之前的81.6 %提高到了92.1 %(表2)，取得了较好的应用效果[20]。

表2 解释符合率统计Table 2 The coincidence rate of interpretation

板A井位于板中东断块，106号层顶部(3 550～3 554.6 m)与109号层，电阻率值较高，均在35 Ω·m左右，岩性纯、物性好，两个层的差异不明显，利用常规解释标准很难将两个层区分开。将本次的研究成果应用在板A井中，两个层的差异明显就体现出来，在定性解释图版中(图4)，106号层顶部落在油水同层区，109号层落在油层区；定量解释结果(图5)与定性结果一致，106号层顶部油水同层，109号层为油层。

图4 板A井106、109号层图版位置Fig.4 Plate location of layers 106 and 109 in well ban A

图5 板A井判别分析解释成果Fig.5 Diagram of discriminant analysis interpretation of well ban A

106(3 550.5～3 554 m)号层和109(3 593.8～3 596.2 m)号层合采，日产油1.58吨，气3 469方，水34.2方，含水95.6 %，试采结果与解释结果一致，验证了研究方法适用性。

4 结 论

利用数理统计技术，建立了函数判别图版和定量评价函数模型，能够将综合反映储层特征的众多信息相结合，在油水层识别方面具有很强的优势。该方法应用在板中东断块油水层识别中见到较好的效果。

1)数理统计方法，能够对已知性质进行提取、归类，适用在储层流体性质识别中；

2)应用数理统计方法，选取目标区块的试采井资料，将对油水层反映敏感的测井资料进行融合、归类，建立的多参数流体性质识别图版与传统的双参数图版对比，效果显著；

3)建立了判别分析函数模型，达到了流体性质的定量判别，在油水层识别中具有智能、快速的优势；

4)在目标区块中应用效果显著，引用多参数，实现了流体识别技术的创新。