深水陆坡区井场海底稳定性评价——以南海松涛深水井场为例

吴 涛,李 列,孙 金,欧阳敏，盖永浩

(1.中海石油(中国)有限公司 湛江分公司， 广东 湛江 524057;2.中国科学院 深海科学与工程研究所， 海南 三亚 572099)

1 引 言

近年来，我国在南海深水油气勘探开发方面持续发力，先后在珠江口和琼东南等深水盆地发现了荔湾、陵水等多个大型油气田[1-3]。除了这些深水盆地，我国南海北部陆坡区的油气水合物资源储量也十分丰富，同样是今后深水油气重点勘探开发区域(图1)。然而，相对于深水盆地，陆坡区海底地形坡度较大，浅层地质条件复杂，因此滑坡风险变大[4-6]，可能严重破坏海底井口、海底管道、通信电缆等水下海底工程结构物，引起井口倾覆、管线折断[7,8]，从而造成重大的经济损失，因此陆坡区钻井必须要考虑海底滑坡的问题。

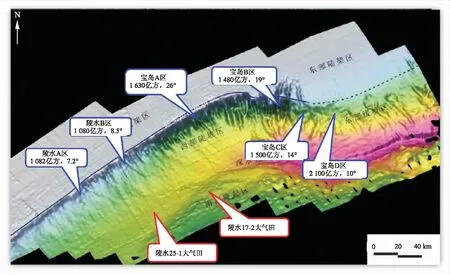
图1 南海北部深水油气田开发区及海底地形Fig.1 Deepwater oil and gas exploitation area and submarine topography of Northern South China Sea

深水海底浅表层土多为软黏土，含水量高，强度很低[9,10]，因此海底斜坡在外力扰动下容易失稳。与陆地滑坡相比，海底滑坡发生时的坡度相对较小，Hance[11]统计了全球399例海底滑坡事件，发现85%海底滑坡的斜坡坡度小于10°；Booth等[12]通过分析海底滑坡发生次数与坡度的关系发现多数滑坡发生时的坡度在2°～10°之间，有时即使坡度小于1°也可能发生滑坡，这大大增加了陆坡区发生海底滑坡的风险。此外，深水钻井表层喷射时对沉积物的扰动、井口装置以及井下返出物作用在海床面上的重量等外界工程扰动都会对海底斜坡的稳定性产生负面影响，增加斜坡失稳的风险，给钻井作业带来非常不利的影响。因此，有必要开展斜坡区深水井场海底滑坡风险的定量评价研究，在满足勘探和开发目的的前提下，原则上应尽量选择滑坡风险最小的区域[13,14]，从而为井位优选和海底滑坡的防治提供重要参考价值。

目前，虽然前人在边坡稳定性评价方法等方面进行了大量的研究[15-20]，然而，对深水陆坡区(特别是考虑钻井影响)的海底斜坡稳定性评价方面却鲜有研究。本文以位于南海北部琼东南海域陆坡区的松涛深水井场为例，利用自主式水下航行器(AUV，Autonomous Underwater Vehicle)地形地貌数据建立了海底斜坡模型，并考虑浅层土强度的垂向非均质性，利用有限差分强度折减法计算钻井过程中的井口附加载荷和钻井振动载荷对海底斜坡安全系数的影响，估计斜坡滑移面的大小和位置，实现深水井场钻井过程中的海底滑坡风险的定量评价。

2 松涛深水井场地形及工程地质概况

松涛区探井位于琼东南陆坡区，为该区第一口探井，海底坡度较大，钻井过程中存在较大的滑坡风险，如何优选井位以确保海底斜坡的稳定性是钻前亟待解决的问题。因此，钻前进行了详尽的井场调查，主要包括多波束水深地形调查、AUV旁扫声呐海底地貌调查、AUV浅地层剖面调查、重力取样、海床式静力触探原位测试、室内土工实验和海底流速观测等。

2.1 井场水深及海底地形

精确的海底地形是进行海底斜坡稳定性分析的关键。为提高地形测量精度，井场调查采用AUV对3 km×3 km范围内的海底地形进行多波束调查(图2)。从水深地形图可以看出，深水井场内水深在1 078.4～1 344.5 m之间变化，整体由西北向东南方向逐渐变深，中部区域海底隆起，呈楔形状，预定井位的北向和西南方向各有一处陡坎，在此处水深和坡度变化较大。在中部海底隆起区域选定了四个备选井位，井位1(图中的W1)的水深为1 189.8 m，井位2(图中的W2)的水深为1 195.8 m， 井位3(图中的W3)的水深为1 188.3 m，井位4(图中的W4)的水深为1 185.8 m。

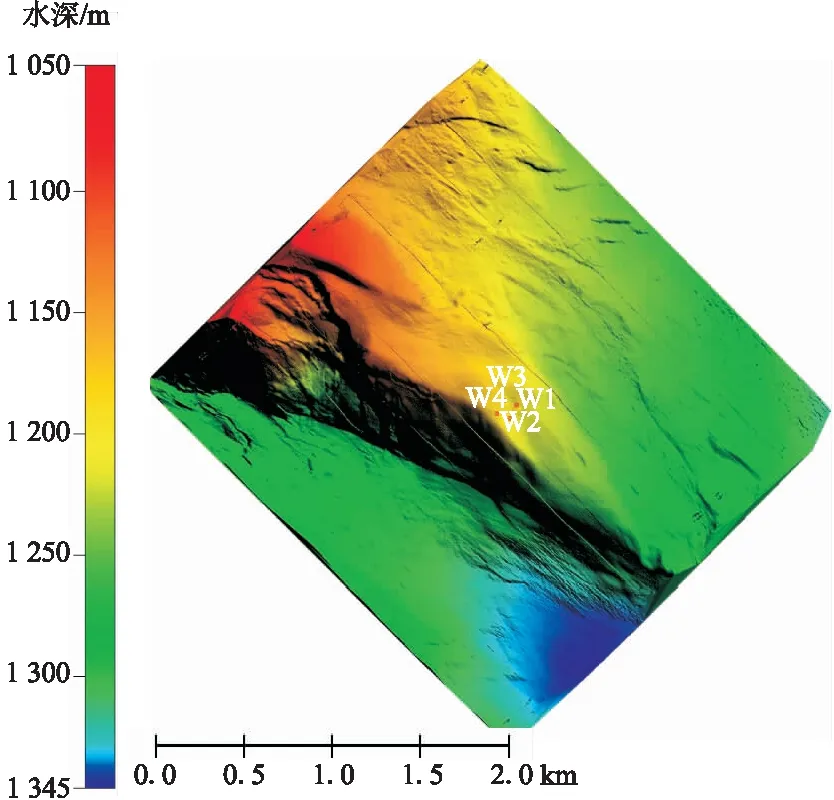
图2 松涛深水井场水深地形(3 km×3 km)Fig.2 Submarine topography of Songtao deepwater drilling site(3 km×3 km)

深水井场的海底坡度变化较大(图3)，在0°～30°之间变化，海底隆起区域的坡度普遍大于其他区域，四个备选井位的坡度也不小，其中井位1的海底坡度约为5.1°，井位2的海底坡度为5.7°，井位3的海底坡度为6.6°，井位4的海底坡度为3.2°，存在海底滑坡风险。

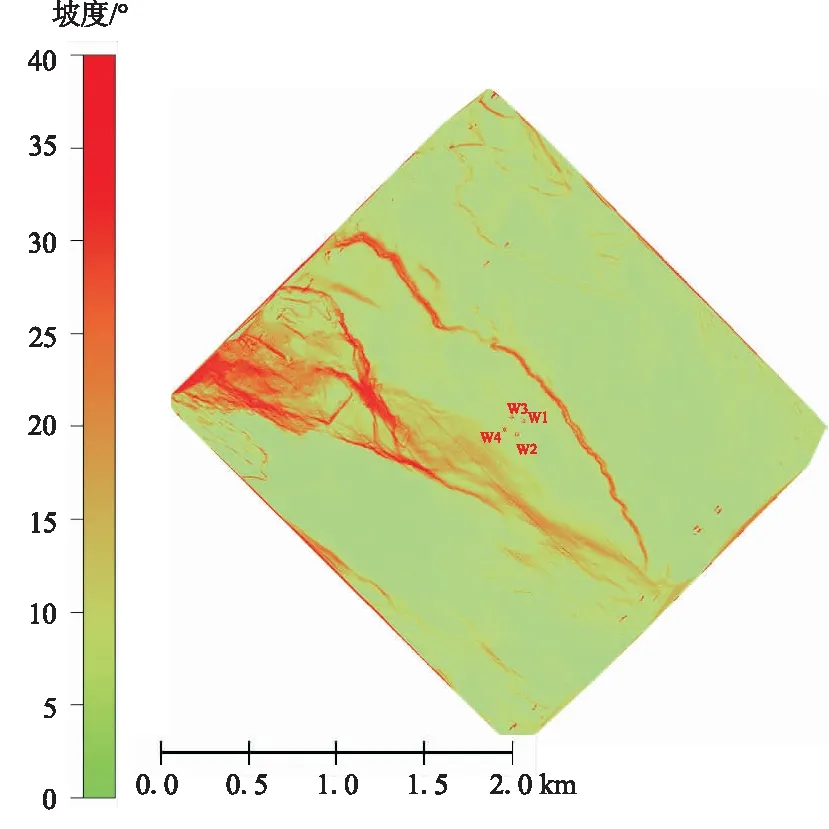
图3 海底坡度Fig.3 Submarine gradient

2.2 浅层地震反映的地质情况

浅层地震可以更清晰地反映浅层地质情况[21]。图4(a)和图4(b)为井场内两个不同方位的浅层地震剖面。浅部地层共分为3层，即A层、B层和C层，相应的反射底界面依次为R1、R2和R3。A层厚度在0 m至9.8 m之间变化，为水平或近水平层理，反射能量较强，地层反射连续性较好；B层在A层之下至反射界面R2之间，多为空白或者弱反射，层理较差，局部区域存在能量较弱的不连续反射结构；C层在B层之下至反射界面R3之间，横向地层反射连续性较好，反射能量较弱，A+B+C层的厚度在16.5 m至33.6 m之间变化。

可见，在井场3 km×3 km井场调查区域内海底至海底以下约40 m深度范围内发现4条断层，且这些断层都是由地层滑塌造成，顶部几乎出露海底或接近海底。在井场调查区域内海底至海底以下约40 m深度范围内发现两处疑似滑坡体(图4)。

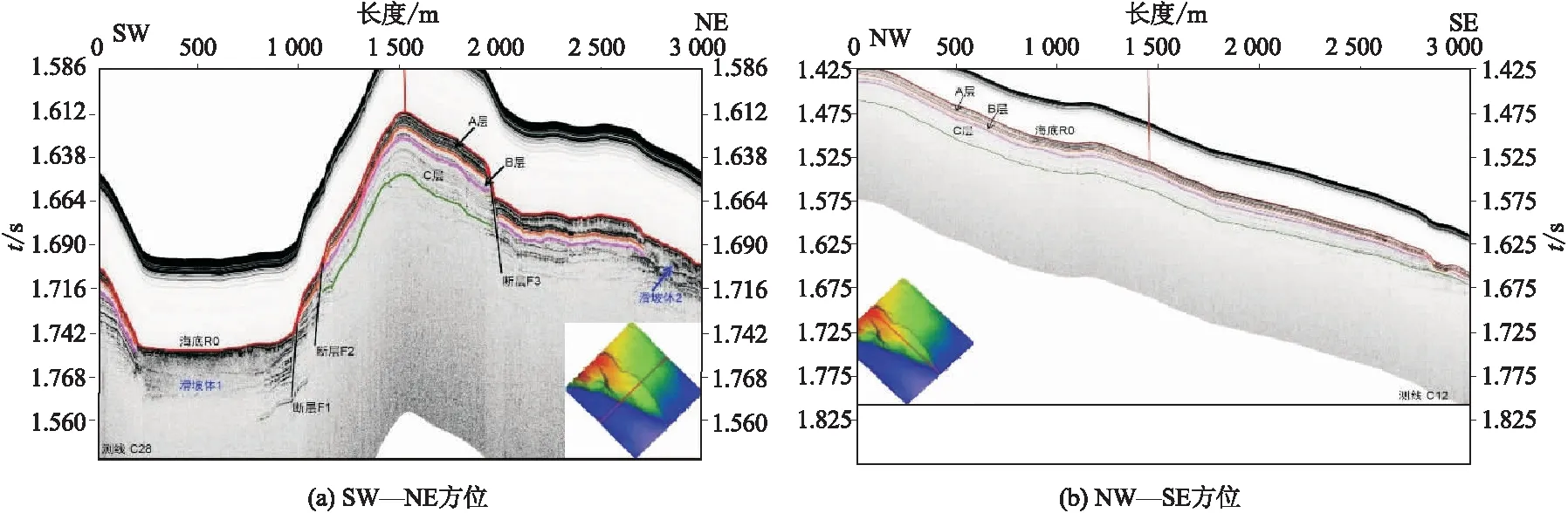
图4 两个不同方位的浅层地震剖面Fig.4 Shallow seismic profiles in two different directions

2.3 海底土土质参数

2.3.1 海底土重力取样土工测试结果

共取得7个站位的样品，样品深度在4.4～4.8 m之间，在室内进行了容重、含水量、液塑限、不排水抗剪强度等物理力学参数的测试。结果表明，海底土为软黏土，湿容重在14.12 ～14.78 kN/m3之间，粒径小于75 μm的土质量百分比接近100 %，说明黏土含量很高；绝大多数沉积物的天然含水量在90 %以上，随深度变化不明显，且均高于液限(液限是指黏性土处于可塑状态与流动状态之间的界限含水率)，液性指数大于1；海底土不排水抗剪强度值基本都在2.0～10.0 kPa之间，且沉积物的不排水抗剪强度随深度增加而增大。

2.3.2 海底土静力触探原位测试结果

受取样深度限制，重力取样仅仅获得了海底以下4.8 m之内的浅表层海底土的物理力学参数，其取样深度对于海底滑坡风险的评估来说还不够，而海床式静力触探(即CPT,静力触探试验Cone Penetration Test)的贯入深度可以达到几十米，因此，井场调查中又进行了海床式静力触探原位测试，海床式静力触探探头贯入深度达20.12 m，根据海床式静力触探测试结果解释得到的不同深度处海底土的不排水抗剪强度见图5。

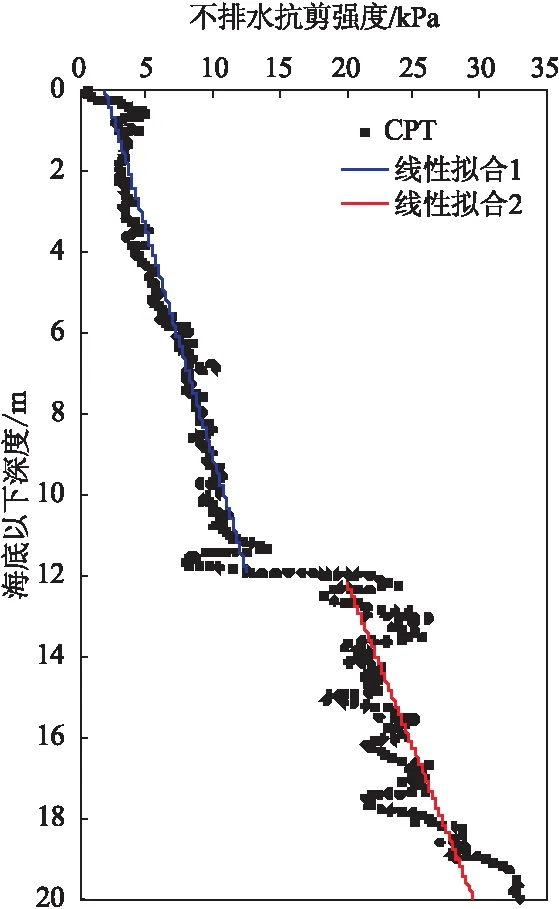
图5 海底土不排水抗剪强度随深度的变化Fig.5 Variation of undrained shear strength of submarine soils versus depth

从图中可以看出，海底土不排水抗剪强度随深度增加呈现出逐渐增大的趋势，在浅层11.7 m左右，海底土强度发生突变，上部强度很小，表层强度仅为0.65 kPa，非常软弱，11.7 m以下海底土强度突然增加约10 kPa，土质描述表明，在该深度处土质类型发生了变化，由软的褐灰色黏土变为稍硬的粉质黏土，这可能是引起强度突变的原因。对0～11.7 m和11.7～21.12 m的海底土不排水抗剪强度与海底以下深度的关系进行分段线性拟合，可以得到海底土不同深度时的不排水抗剪强度：

1)当海底以下深度z小于11.7 m时，海底土的不排水抗剪强度qu为

qu=0.8913z+1.888 0

(1)

式中，qu为不排水抗剪强度，kPa；z为海底以下深度，m。

2)当海底以下深度z大于11.7 m时，海底土的不排水抗剪强度qu为

qu=1.217 8z+5.194 8

(2)

在海底稳定性分析时采用式(1)和式(2)表征海底土不排水抗剪强度的垂向非均质性。

2.4 海底流速

采用深水潜标对海底流速进行了持续两个月的观测，图6为表示流速—流向联合概率分布的海流玫瑰图。可见，在海底之上10 m层，海流最大流速为16.7 cm/s，概率约8.1 %，方向NNW，最小流速为0.06 cm/s，概率约2.5 %，方向SSE，平均流速为5.4 cm/s，流向集中在NW-SE；海底之上20 m层，最大流速为16.4 cm/s，概率约11.6 %，方向NNW，最小流速为0.15 cm/s，概率约3.2 %，方向SSW，平均流速为4.8 cm/s，流向集中在NW-SE。综合来看，海底水流为往复运动，平均流速约为5.1 cm/s，海底水体整体较安静，对海底斜坡稳定性并未构成实质影响。

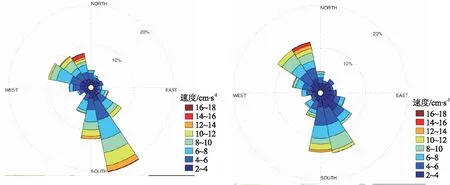
图6 表示流速-流向概率分布的海流玫瑰Fig.6 Rose diagram of seawater veloctiy indicating the probability distribution of magnitude and direction of flow velocity

3 斜坡稳定性分析方法

本研究使用安全系数Fs评价海底斜坡的稳定性，安全系数Fs定义为滑动面上的平均抗剪强度与平均剪应力的比值，即

(3)

式中，c0为地层黏聚力，MPa；σ为滑动面上的正应力，MPa；φ0为内摩擦角，°；τ为滑动面上的剪应力，MPa；A0为滑移面面积，m2。

安全系数Fs表征了斜坡的安全储备大小，当Fs大于1时，斜坡稳定；Fs等于1时，坡体处于极限平衡状态；安全系数Fs小于1时，斜坡即发生破坏。基于强度折减法的斜坡稳定性数值模拟是一种将强度折减法与弹塑性数值方法相结合的斜坡稳定性分析方法，其基本原理是先引入某一强度折减系数F将土体的抗剪强度(黏聚力和内摩擦角)进行折减，得到折减后的强度参数，具体做法如下：将沉积物原来的黏聚力和内摩擦角进行折减[22]：

(4)

式中，F为强度折减系数。

4 松涛深水井场海底稳定性静力学分析

4.1 钻井对海底斜坡稳定性的影响

深水钻井对海底斜坡来说是一种工程扰动，会对其稳定性造成一定的不利影响，究其原因，主要包括以下两个方面的作用：

1) 水下井口装置和钻井返出岩屑的重力载荷

深水钻井时钻井平台或钻井船漂浮在海面上，而井口在海底，因此其钻井装备与陆地钻井有很大不同[23]，为实现正常钻井，需要在水下装设一套隔绝海水、适应平台升沉摇摆、控制井口的装置，即深水钻井水下装置，而安装在海底用于控制井口的装置称为水下井口装置，主要包括防沉板、高压井口头、水下防喷器等，其重量可达几十吨。不过，高压井口头、水下防喷器等井口装置的重力载荷并非直接作用于海床面上，而是坐挂在表层导管上，表层导管通过喷射钻井下入海底以下数十米的深度，这样水下井口的重量可通过表层导管与浅层沉积物之间的相互作用支撑，因此，水下井口的重力载荷对海底斜坡稳定性的影响较小。

深水钻井中，表层套管井段为开眼循环钻井，一般直接使用海水作为钻井液，钻出的岩屑直接堆积在海床上，因此与水下井口装置相比，井口返出岩屑对海底斜坡稳定性的影响更大，井口返出岩屑的重量可用下式计算

(5)

式中，Ws为井口返出岩屑的重量，t；ρs为沉积物的密度，t/m3;D1和D2分别为导管段和表层套管段的井眼直径，m；H1和H2分别为导管段和表层套管段的井深，m。

如果假设沉积物的平均湿密度为2 150 kg/m3，则对于36 in的导管以及20 in的表层套管来说，其对应的井眼直径则分别为914.4 mm和558.8 mm，目前多数深水井的导管入泥深度为100 m以内，表层套管下深为500～800 m[24]，这里令导管段深度为100 m，表层套管段为800 m，则井口返出岩屑的重量为510.3吨。数百吨的返出岩屑堆积在井口附近的海底上会在海床面上产生附加重力载荷，引起斜坡面上所受的正应力和剪应力载荷增大(图7)，诱发井口附近的海底斜坡失稳。

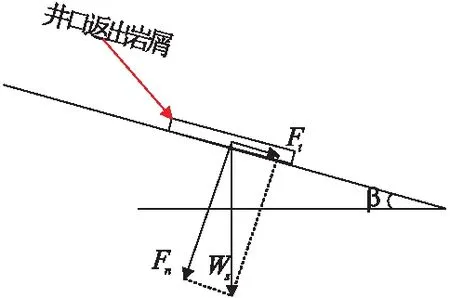
图7 井口返出岩屑在海底引起的附加载荷Fig.7 Additional load on the seafloor caused by returned cuttings from borehole

井口返出岩屑在海床面上引起的附加正应力和剪应力载荷分别为

(6)

(7)

式中，β为斜坡坡角，°；Fn和Ft分别为重力载荷分解产生的法向力和切向力，N；σn和σt分别为附加载荷引起的海床面上的正应力和剪应力，Pa；A为井口返出岩屑在海底的分布面积，m2。可见，井口返出岩屑越多，Ws越大，引起的附加应力越大，斜坡越不稳定。

2)钻井扰动产生的动载荷

深水钻井过程中，表层导管通过喷射方法下入，高压射流对浅层沉积物的破碎作用会在井眼附近产生动载荷，表层导管安装完成后，后续的表层套管段则通过钻头钻进，钻头在钻压和旋转作用下破碎地层，从而产生一定强度的振动载荷，可能诱发斜坡失稳。

4.2 海底斜坡稳定性的静力学分析

暂不考虑钻井扰动产生的动载荷的影响，利用静力学分析方法分析海底斜坡在重力和井口返出物附加载荷下的滑坡风险。为概化海底斜坡的地质力学模型，静力学分析时做了如下4点假设：

1)不考虑土体液化的影响作用；

2)不考虑沉积物层内部的渗流作用，但考虑静态孔隙压力作用；

3)假定沉积层与水合物带服从于摩尔-库仑强度准则；

4)海底滑坡是一种突然的能量释放过程，沉积物在很短的时间内来不及排出，因此其强度应采用不排水强度。

根据海底地形地貌数据以及钻探目的要求，在4个备选井位中选取了2个井位，其中井位1为靶点位置，该处坡度大约为5.1°，为降低海底滑坡风险，在靶点东北方向556m处又选择了井位2，其坡度大约为3.2°。

4.2.1 几何模型

几何建模时选择过两个井位不同方向的3个剖面作为计算剖面，剖面位置及建立的几何模型如图8和图9所示。

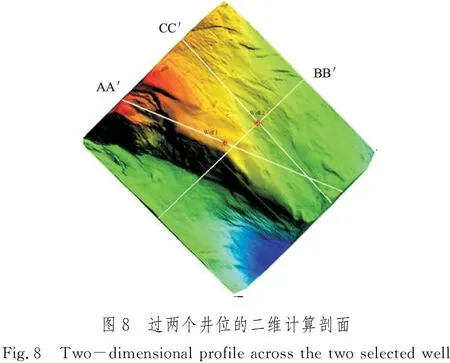
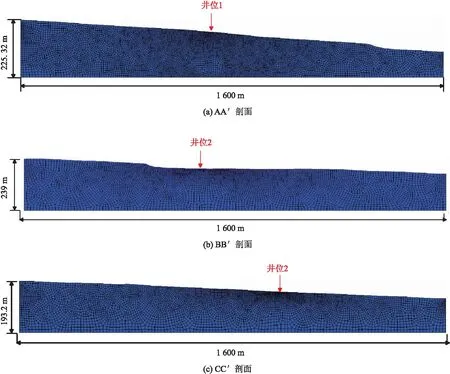
图9 海底斜坡几何模型Fig.9 Geometric model of submarine slope

4.2.2 边界条件与初始条件

整个模型为平面应变模型，模型底部为固定边界；约束模型左右侧面的法向位移；坡面设为自由边界。对于流体边界条件，坡面处令孔隙压力等于海底静水压力，模型侧面的孔隙压力等于相应深度处的静水压力，模型底面为非渗透边界条件，对于载荷条件，沉积物层顶面节点施加海水产生的静水压力，并假设返出的碎屑分布在井口附近20 m2的区域，在此区域内施加井口附加载荷，坡面上的法向和切向载荷按式(5)计算。初始条件中，对整个模型施加由沉积物自重和海水压力产生的初始应力场以及静水孔隙压力。

4.2.3 海底斜坡安全系数及临界失稳时的塑性区和潜在滑移面

表1为计算得到的三个剖面对应的安全系数。可见，井位2处的海底斜坡安全系数更大，钻井过程中海底滑坡风险更低，因此，选择井位2作为钻井井位更为安全。

表1 海底斜坡安全系数Table 1 Factor of safety of different slope profile

通过塑性区可直接观察海底斜坡临界失稳时的剪切屈服情况(图10)。对于过井位1的剖面AA′，当强度折减相应值后，塑性区首先出现在井口附近和井口下部的陡坎部位，说明这些区域首先发生了塑性剪切破坏，其中井口附近的塑性破坏是由井口附加载荷造成的，陡坎部位的塑性破坏是由于坡度过大造成的；对于过井位2的剖面BB′，井口附近和上部陡坎都出现了不同程度的塑性屈服区，井口附近的塑性区面积要小于上部陡坎部位，说明相比于井位附近，陡坎处更易发生海底滑坡；对于过井位2的剖面CC′，塑性破坏发生在井口附近，其它区域未见破坏。

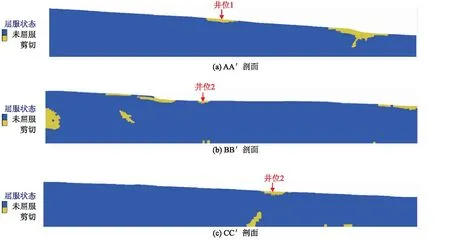
图10 斜坡临界失稳时的剪切塑性区Fig.10 Shear plastic region of submarine slope when loss stability

岩土在压缩过程中的破裂面与剪应变破坏带非常一致[25]，因此可以利用剪应变增量来判断潜在滑坡体和滑移面，图11为海底斜坡临界失稳时的剪应变增量。对于AA′剖面，在井口和陡坎处，海底土的剪应变增量均大于0，说明这两个部位均有发生滑移的趋势，且由于井口返出岩屑附加载荷的影响，井口处的剪应变增量更大，表明井口附近斜坡更易失稳，最大滑坡深度约为12 m；对于BB′剖面，在井口和陡坎处的沉积物剪应变增量均大于0，说明这两个部位均有发生潜在滑移的趋势，且上部陡坎处滑坡体的体积要大于井口处的滑坡体，上部陡坎处的最大滑坡深度约为20 m；对于CC′剖面，只在井口附近存在滑移趋势，最大滑坡深度约为14 m。

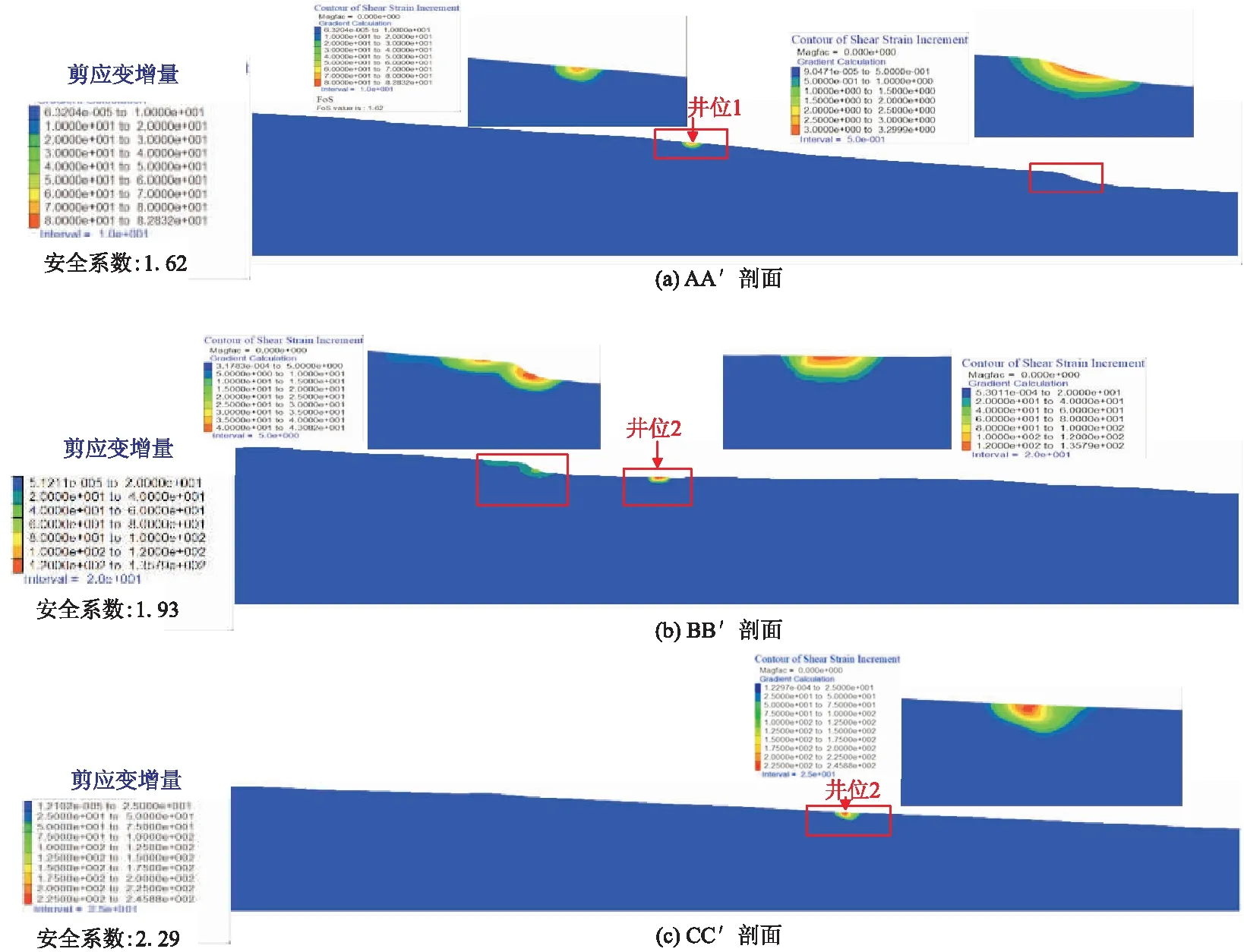
图11 斜坡临界失稳时的剪应变增量Fig.11 Shear strain increment of submarine slope when loss stability

5 钻井扰动下的海底斜坡稳定性

除了井口附近的附加静载荷，由钻杆上下左右活动、钻头破碎地层和表层喷射导管的喷射作用等造成的钻井扰动也可能对海底斜坡的失稳产生影响。然而，这些作用力是变化的，很难精确计算，但是这些变化的力施加在周围地层时最终是通过振动波来影响的，即地层会产生相应的振动，可以用速度或加速度表征。选择安全系数最小的AA′剖面，在井眼范围内(图12中竖直的红线，表示直径36 in的井眼)施加一频率为20 Hz的横向和垂向正弦速度扰动，模拟钻井过程中井眼周围的钻井扰动。同时，在坡面选择5个位移监测点，各监测点距井眼的距离依次为11.6 m、212.1 m、512.7 m、189.4 m、389.8 m和609.5 m，计算过程监测每个监测点位移随时间的变化(图13和14)，从而判断不同的峰值速度对斜坡稳定性的影响。

图12 井眼附近动载荷的施加及位移监测点的位置Fig.12 Imposition of dynamic load near the well and position of displacement monitoring point

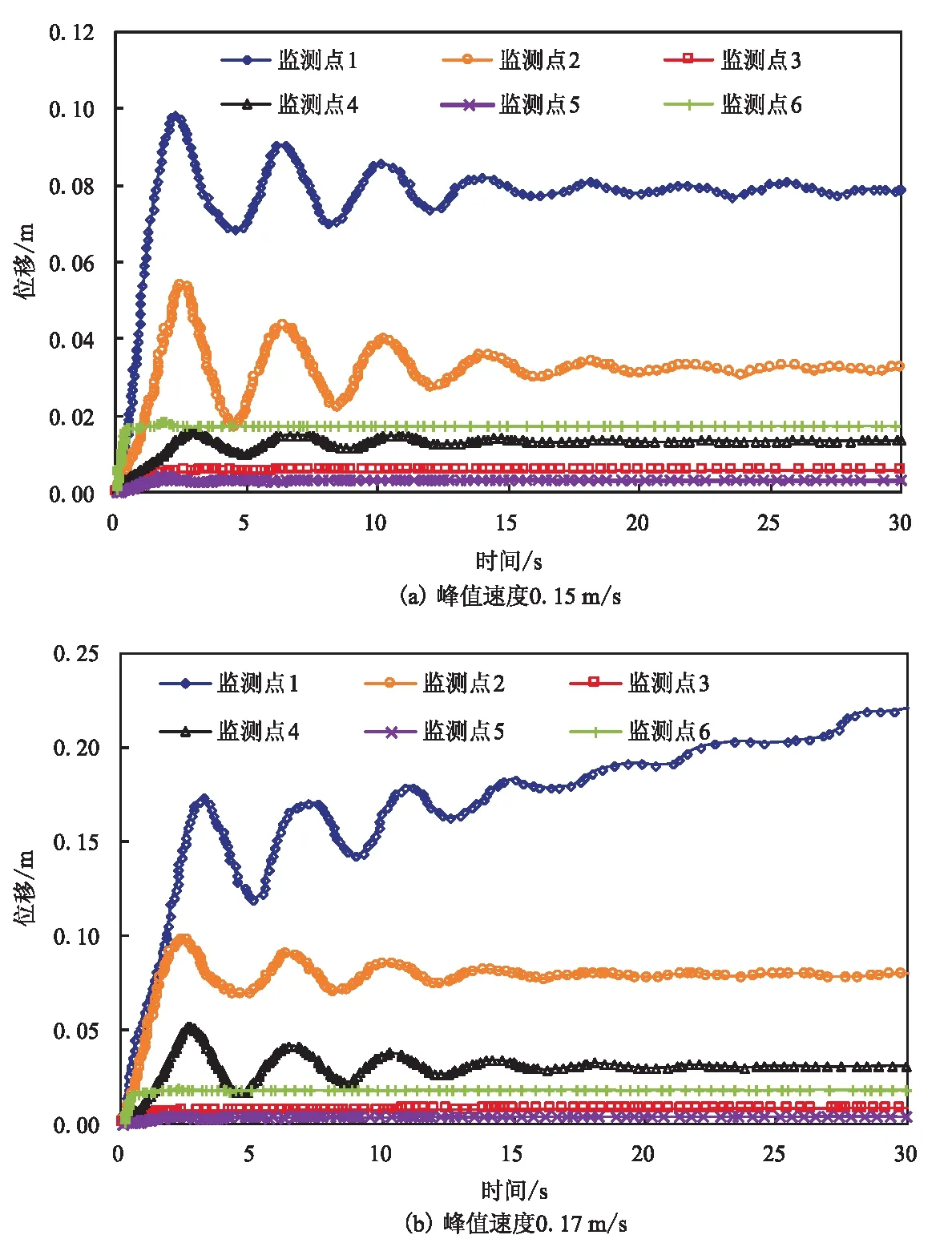
图13 横向扰动下各监测点位移随时间的变化Fig.13 Variation of displacement of monitoring points versus time under the lateral disturbance

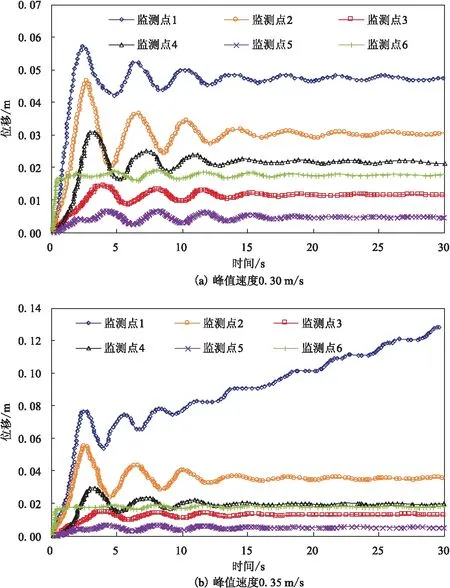
图14 垂向扰动下各监测点位移随时间的变化Fig.14 Variation of displacement of monitoring points versus time under the vertical disturbance

由图13可见，施加横向扰动后，各监测点的位移在开始阶段逐渐增加，之后监测点位移在沉积物自身阻尼的作用下逐渐变小，位移最大值位于距井眼最近的监测点1，监测点5处位移最小，监测点6处由于存在陡坎，故虽然距井眼较远，但位移在自身重力作用下也较大。当横向峰值速度为0.15 m/s时，各监测点位移随时间趋于稳定，说明此时斜坡不会失稳；当横向峰值速度继续增加到0.17 m/s时，监测点1处的位移随时间快速增加，此时斜坡失稳风险大大增加。由图14可见，施加垂向扰动后，位移最大值位于距井眼最近的监测点1，监测点5处位移最小，当垂向峰值速度为0.30 m/s时，各监测点位移随时间趋于稳定，说明此时斜坡不会失稳；当垂向峰值速度增加到0.35 m/s时，监测点1处的位移不断增加，其它监测点位移逐渐趋于稳定，说明此时监测点1在外界扰动下可发生持续滑动，斜坡有较大的失稳风险。与横向扰动相比，垂向扰动时监测点处的位移相对较小，斜坡失稳时的峰值速度更大(0.35 m/s)，表明钻井时横向扰动时斜坡失稳的风险比垂向扰动更大。横向和垂向扰动下斜坡开始失稳时的峰值速度分别对应于地震烈度表中的7级烈度和8级烈度，而钻井时一般不会在地层中产生这么大的峰值速度，因此，钻井扰动引起的海底滑坡风险非常小。

该井钻井方案选择本研究推荐的井位2作为井口位置，于2018年5月底开钻，实际钻井过程中未发生海底失稳。

6 结论与建议

1)深水钻井对海底斜坡稳定性的影响主要包括水下井口装置、钻井返出岩屑的重力载荷以及钻井扰动产生的动载荷。

2)返出岩屑引起的附加载荷降低了海底斜坡安全系数，增加了井口附近海底斜坡失稳的风险；钻井横向扰动比垂向扰动更易引起海底滑坡，但所需的峰值速度较高，很难引起海底斜坡的失稳。

3)松涛深水井场海底坡度在0°～30°之间变化，备选井位附近坡度在5°左右，存在一定的海底滑坡风险。计算结果表明，潜在滑移面位于井位或陡坎附近，不过斜坡安全系数均大于1.0，相对于井位1，井位2处的安全系数更大，滑坡风险相对很小，因此选择井位2作为最终井位，实际钻探结果表明，所选井位未发生滑坡。

4)目前，深水井场斜坡稳定性评价在海底土工参数测试和预测、稳定性计算方法、行业规范制订等方面尚处于初步研究阶段，今后应在浅层土物理力学参数空间分布规律的预测、三维海底斜坡稳定性数值模拟、钻井扰动对海底斜坡稳定性的影响、不同工况下海底斜坡安全系数标准等方面开展更深入的研究。