基于改进极限学习机的食品安全风险预测研究

陈硕峰，石怀明，郭承湘，刘康康，陈宁江,4

(1.广西大学 计算机与电子信息学院， 广西 南宁 530004；2.广西壮族自治区食品药品安全信息与监控中心， 广西 南宁 530029；3.广西中医药大学校长办公室、发展规划处、网络和信息化管理办公室(合署), 广西 南宁 530200;4.广西高校并行与分布式计算技术重点实验室， 广西 南宁 530004)

0 引言

食品安全问题一直是国家重点关注对象，近年来跟随着国家的食品安全监管战略的实施，各个食品监督管理部门都建设了业务管理系统，实现信息化监管，随着食品监管工作的信息化、智能化，工作效率也日益提升，积累的数据也越来越多[1]。但这些积累下来的食品监管数据面临着数据混乱冗杂、整合利用程度低、挖掘不充分等问题，利用率很低[2]，大多数还处于信息记录、备案阶段，只有少量的数据应用到分析图表上,食品检测数据并没有得到充分的利用，也未能有效地利用现有数据来提高发现食品潜在风险的机率。

本文针对食品监管数据中的隐藏信息提出了一种加权粒子群算法的极限学习机模型(加权PSO-ELM)，利用现有数据实现对食品检测的预测。本文研究对象为某省食品药品监督管理局的食品日常抽检数据，结合抽检数据的分布不平衡的规律，该模型基于加权极限学习机[3]进行分类预测，同时针对极限学习机(extreme learning machine, ELM)算法的参数使用粒子群算法(partical swarm optimization, PSO)进行优化。考虑到实际食品抽样中正负样本不平衡，即抽检结果为合格的数据量过多而结果为不合格的数据量过少，这会导致对人们关注的不合格样本预测结果不够理想的问题，因此，使用一种加权处理方法，提高对抽样结果为不合格的少数样本预测结果的准确度。最后，为了验证模型预测结果的可信度，基于历史数据使用贝叶斯网络模型[4]计算在食品抽检结果为不合格的情况下食品数据的后验概率，以此验证改进极限学习机预测结果的可靠性。

1 模型设计

1.1 加权PSO-ELM

ELM能够在极快的学习速度下获得很好泛化性能，现在ELM在图像识别、自然语言处理、文本情感分析等各领域的应用都展现了其快速学习的能力和精确度，因此ELM在对食品安全风险预测方面也会有适用的优势[5]。在单隐藏层神经网络ELM中，假设有N个任意的样本(Xi,ti)，其中Xi=[xi1,xi2,…,xin]T∈Rn为输入值，ti=[ti1,ti2,…,tim]T∈Rm，并假设隐藏层有L个节点，则其表达式如式(1)所示:

(1)

式中，g(x)为激活函数;Wi=[wi1,wi2,…,win]T为输入权重;βi为输出权重;bi是第i个隐藏层单元的偏置;oj为样本预测值。Wi·Xj表示Wi和Xj的内积。

为了获得最优解，需要定义一个损失函数，其表示如式(2)所示:

(2)

式中，oj为样本的预测值;tj为样本的真实值。

只有当输出误差达到最小，此时的解才是最优解，即存在βi、Wi和bi，使得式(3)成立:

(3)

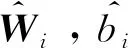
(4)

式中，i=1,…,L，这相当于最小化损失函数，损失函数如式(5)所示:

(5)

但是考虑到ELM算法的求解很大程度依赖一定的输入权集和隐藏偏置，虽然实现了求解线性系统全局极小点，但是在不同的输入权集与隐藏偏差可能具有不同的性能，所以它可能不是问题空间的全局极小点，故需要对ELM输入权集以及隐藏偏置进行优化。

众所周知，进化算法是可以通过全局搜索策略来避免局部极小问题，而PSO算法作为一种进化算法，其前期收敛速度快，能够极快逼近最优解[6]。除此之外，使用PSO优化算法还不需要手动决定或者旋转参数，故使用PSO算法对ELM进行优化。与此同时，考虑到本文所研究的食品安全检测中的实际情况，大部分食品的检测结果是合格的，导致抽检数据中正负样本数量上的巨大差距，继而导致在对食品安全风险预测中对抽检结果为不合格的样本预测的不理想，但是抽检结果为不合格的少数类数据是人们更加关注的，所以使用加权法对PSO算法进行优化，在进行数据处理时提高对少数样本的关注，研究处理数据不平衡的加权方案[7]。

在PSO算法中，设有一个N维空间，其中有n个只有位置信息和速度信息的粒子，则第i个粒子在空间中的位置为Xi=(x1,x2,…,xn)，飞行速度为Vi=(v1,v2,…,vn)。pbest表示某个粒子目前的最优解，gbest表示所有粒子中的最优解。PSO算法是通过不断更新pbest和gbest来寻找最优解的，而定义的适应度函数计算所得的适应度值就是在某一轮迭代中是否更新pbest的判断标准。

第一种加权方案如式(6)所示：

(6)

式中，count(ti)为训练样本中检测结果为ti的样本数量。

对于本文研究对象来说抽检结果只有合格与不合格两种，因此上述方法的权值分子都是1，分母分别为两种抽检结果的样本数量。

第二种加权方案如式(7)所示：

(7)

这种加权方案的结果只有两类，而且将少数类和多数类的权值比例控制在0.618∶1(黄金分割比)，实际上是以牺牲多数类的分类精度换取少数类的分类精度。结合食品的实际检测情况，此方案中抽检结果为合格属于多数类，抽检结果为不合格属于少数类。

在食品安全问题领域中，由于大部分食品的检测结果是合格的，这就导致抽检数据中正负样本数量上的巨大差距，会导致在对食品安全风险预测中对不合格的样本预测的不理想。但是不合格的少数类数据是更加受关注的。在方案一中，更加适用于有多种抽样结果而且加权权重相同的数据处理，相比之下，方案二是将抽样结果分为少数类和多数类两类，而且是牺牲多数类的分类精度来提高少数类的分类精度，更符合本文的要求。

在PSO算法中分别为输入权重、输出权重、偏置设置粒子群，运行结束后会得到输入权值、输出权值、偏置的参数矩阵[8]，通过使用式(7)中的加权方法对输出权值进行二次加权，便得到加权PSO算法训练结果，将该结果作为ELM的参数。由于ELM需要优化的参数为权值和阀值，其适应度函数[9]可用式(5)进行表示，即求目标函数min(E)。加权PSO算法步骤如下：

输入：训练样本

输出：极限学习机所需的输入权值、输出权值、偏置

① 设置种群大小N、最大迭代次数M及学习因子c1、c2;

② 循环执行如下操作，直到当前迭代次数等于最大迭代次数M;

③ 对每个粒子i;

④ 计算其适应度fit(i);

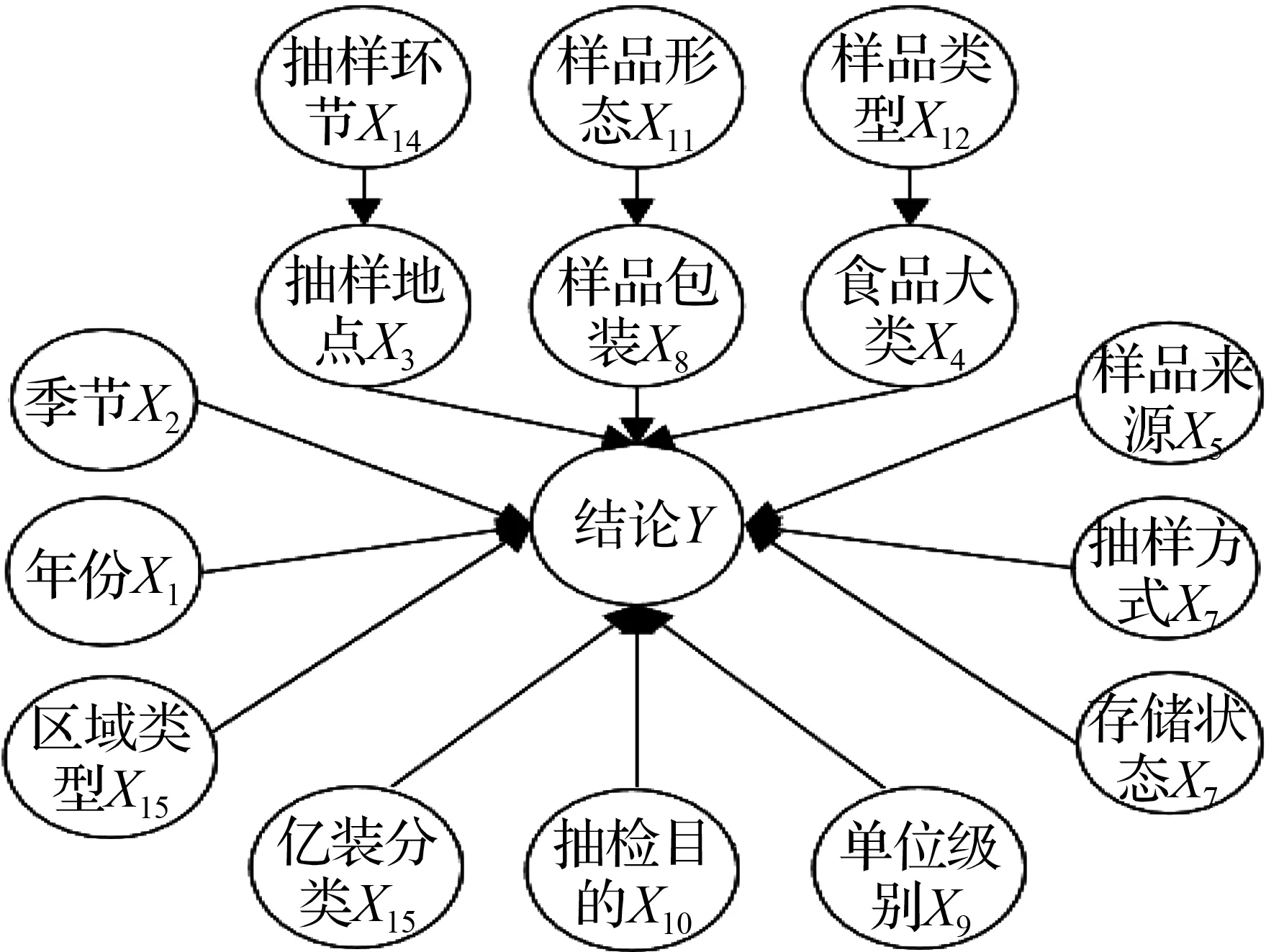
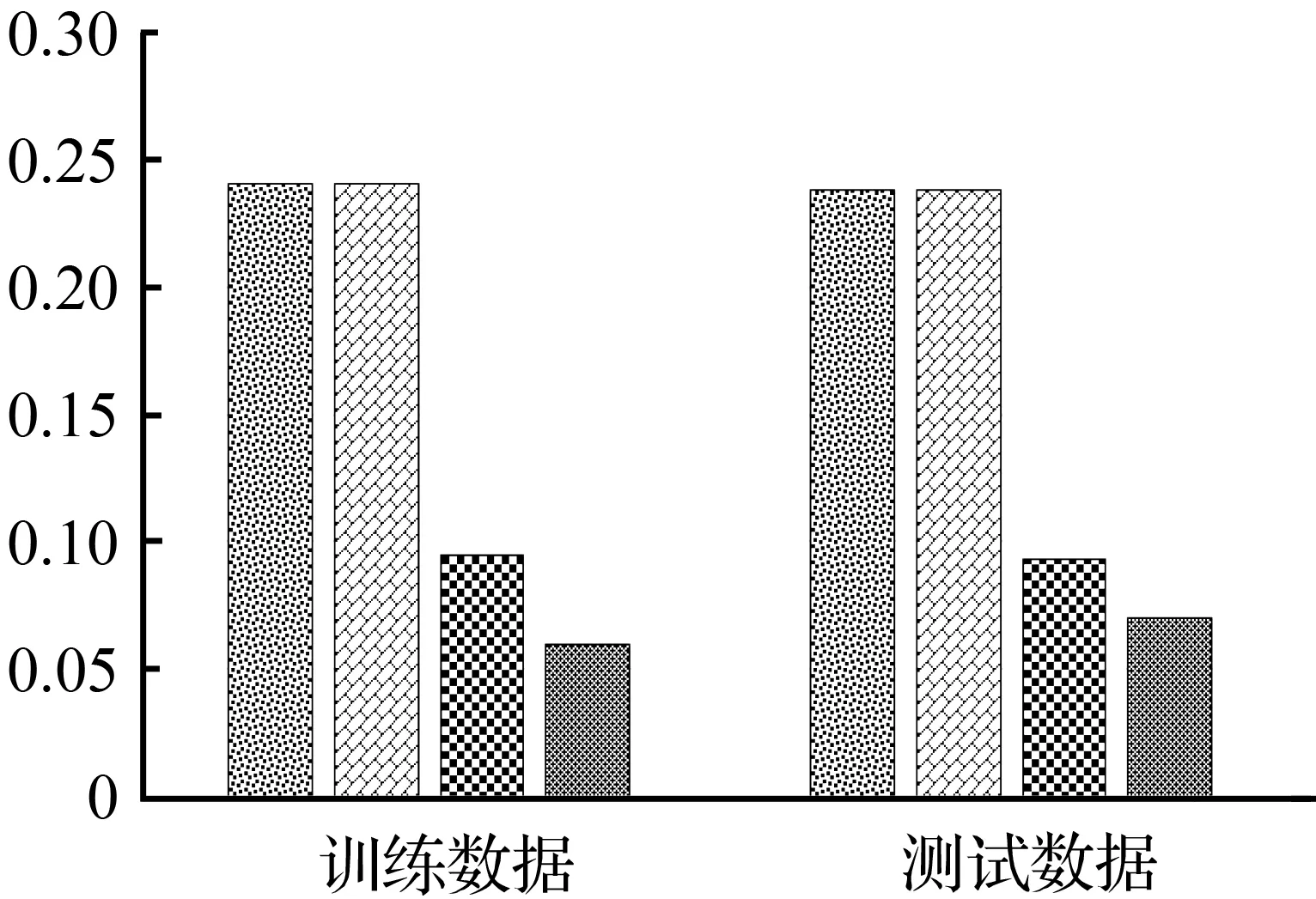
⑤ 如果fit(i)

⑥ 如果fit(i)

⑦ 更新粒子位置：xi=xi+vi;

⑨ 对输出权重粒子群的历史最优粒子位置，根据式(7)进行加权;

其中，rand()可以产生0和1之间的随机数，c1和c2为学习因子，ω为惯性因子。加权粒子群算法训练得到的输入权重、输出权重和偏置作为极限学习机的参数，从而得到加权PSO-ELM，用此模型对食品安全风险进行分类预测。

1.2 贝叶斯网络模型

本小节使用贝叶斯网络模型对上一小节的预测结果的可信度进行验证。首先对加权PSO-ELM的预测结果进行统计，分析预测结果为不合格的数据中各个字段中占比最高的取值。然后根据各个字段之间的关系建立贝叶斯网络，在通过历史数据计算出所有先验概率，最后计算所需后验概率(即不合格的情况下各个字段取到的概率)，找出各个字段中概率最高的取值，将结果与人工神经网络阶段的预测分析结果进行对比，判断预测结果是否可信。

根据字段关系建立的贝叶斯网络如图1所示，其中X1至X15为特征字段，Y为抽检结果，箭头终点字段受起点字段影响。

图1 贝叶斯网络

部分先验概率见表1。

表1 部分先验概率

计算后验概率的公式分为三类(Y=1表示抽检结果为不合格，xi为特征字段)：

第一类求P(xi|Y=1)，i=2,5,6,7,9,10,13,15。这类后验概率的公式如式(8)所示：

(8)

式(8)在计算时，对于xj变量，需要使用改式分别计算xj变量各个取值下的概率，如计算P(x2|Y=1)，需要分别计算P(x2=1|Y=1)、P(x2=2|Y=1)、P(x2=3|Y=1)、P(x2=4|Y=1)，这样即可知道对于某一个变量xj，在抽检结果为不合格的情况下，该变量的哪一个取值出现的概率最高。

第二类求P(xi|Y=1)，i=3,4,8。这类后验概率的公式如式(9)所示：

(9)

式中,xj为xi的前驱节点，即由xj到xi的单箭头。公式(9)的计算和公式(8)类似，对于每一个xi，也需要计算该变量各个取值下的概率(其中xi取某个值时对应的xj有多个取值情况，需要将这些情况下计算得到的概率值相加，得到xi的某个取值的概率)。

第三类求P(xi|Y=1)，i=11,12,14。这类后验概率的公式如式(10)所示:

(10)

式中,xi为xj的前驱节点，即由xi到xj的单箭头。式(10)的具体计算方式和式(9)类似。

2 实验

本文选择了基于LMA的神经网络[10-11]、基于GA的神经网络、基于BP的神经网络[12]、极限学习机及贝叶斯网络来进行实验分析。在进行实验之前，首先对源数据进行预处理，经数据预处理后共计9 025条数据，取75%作为训练集，25%作为测试集；然后进行数据转换，将文本型数据转为数值型数据，并将数据进行归一化至[0,1]内，最后进行数据规约，选出来最重要的14个属性。

相关对比模型参数主要包括：加权PSO-ELM模型的迭代次数设置为20次，粒子群规模设置为20，隐藏层节点数设置为20，精确度阈值设置为0.000 001；基于LMA的神经网络的隐藏层节点数设置为10；基于GA的神经网络的隐藏层节点数设置为2；BP神经网络隐藏层节点数为8；核极限学习机的隐藏层节点数为150。上述网络结构中的隐藏层节点数为模型准确率最高的情况下的隐藏层节点数。

加权PSO-ELM和3种模型的性能对比如图2所示。从图2中可见，LMA神经网络和GA神经网络在训练数据集和测试数据集上的表现都不够好；而加权PSO-ELM和BP模型在训练数据集上都表现较好，但BP在测试数据集上表现相对较差。综上所述，加权PSO-ELM模型表现最好。

(a) MSE对比

ELM优化前后的性能对比如图3所示。从图3可以看出，单纯使用加权法对于ELM的性能没有任何改变，单纯使用PSO算法模型性能得到了极大提升，说明PSO算法可以对ELM的输入参数进行有效优化；在PSO算法优化ELM的基础上结合加权法使得模型性能有进一步提升，准确率得到提高，因此可以得出加权PSO-ELM模型能较好提高预测准确率。另外，还对加权PSO-ELM模型进行了多次实验，发现该模型在测试数据上的预测准确率始终稳定在92%左右，表明该模型具有较强的稳定性。

(a) MSE对比

另外，与文献[5]提出的基于径向基核函数(RBF_kernel)的极限学习机、基于线性核函数(Lin_kernel)的极限学习机进行了对比，这两种模型在文献[5]中被用于肉制品安全的预测。将文献[5]的2种模型与加权PSO-ELM模型在本文所使用的数据集上进行测试后发现，加权PSO-ELM模型对于本文研究对象的预测具有较高的准确率(表2)。

表2 与其他研究者成果对比

表3是加权PSO-ELM预测结果为不合格的数据中各个字段占比最高的取值及其占比，表4是贝叶斯网络模型计算得到的历史数据中在抽检结果为不合格的情况下各个字段中后验概率最高的取值。由于年份字段的研究意义不大，所以这两个表中都去除了年份字段。

表3 加权PSO-ELM预测结果统计

表4 贝叶斯网络各字段概率最高取值

结合表3和表4可以看出，通过对两个阶段结果的分析和相互印证，最终得出结论：加权PSO-ELM的预测结果符合过往历史数据中隐藏的规律，因此其预测结果具有较高的可信度。工作人员可以结合贝叶斯网络阶段的结果(表4)有针对性的进行日常抽检，节省人力资源、提高工作效率。

3 结语

本文针对某省食品药品监督管理局的食品日常抽检数据正负样本不平衡的问题提出了一种加权PSO-ELM模型，主要是首先通过粒子群算法计算得到极限学习机所需的输入权重、输出权重、偏置这3个参数，然后对输出权重进行加权，最后将这3个参数输入极限学习机进行预测。该模型在预测准确率上相比其他对比的模型具有更好的效果，与优化前相比也有所提升，同时也通过贝叶斯网络模型对历史数据的分析验证了加权PSO-ELM模型预测结果的高可信度。本文提出的加权PSO-ELM模型虽然准确率较高，且具有极好的稳定性，但在预测准确率达到92%左右后增加迭代次数，准确率都不会再增加，而且在贝叶斯-人工神经网络两阶段模型中，虽然是通过两个阶段的结果相互印证来验证模型的可靠性，但是两个阶段的结合并不充分。因此，下一步工作考虑将贝叶斯网络模型计算得到的结果转化为第一阶段权值的一部分来改进加权PSO-ELM模型，探索进一步提升准确率的途径。