基于优化组合预测模型的滑坡发展趋势评价

彭亮，田浩，白刚刚，霍宇翔

(1.青海省水文地质工程地质环境地质调查院， 青海 西宁 810008；2.青海省水文地质及地热地质重点实验室， 青海 西宁 810008；3.成都理工大学 环境与土木工程学院， 四川 成都 610059)

0 引言

近年，我国水利建设得以快速发展，在带来巨大经济效益的同时，也间接诱发了一定的地质灾害，如三峡工程修建，诱发复活了大量古滑坡，严重威胁区内居民生命财产安全及长江航运安全；同时，鉴于三峡库区堆积层滑坡相对较多，所占比例达40.6%，进而得出开展三峡库区堆积层滑坡研究具有重要意义[1-3]。由于滑坡发展趋势评价有助于其灾害防治，进而开展其研究具有重要意义。在滑坡发展趋势评价方面，陈菲等[4]利用统计分析评价了滑坡裂缝发展趋势；李明辉等[5]则在滑坡复活机理分析基础上，开展了滑坡发展趋势评价；前述两者也为滑坡发展趋势评价提供了相应思路，但均缺少基于滑坡现场监测成果的发展趋势研究，进而仍需进一步拓展研究。因此，本文以藕塘滑坡为例，通过总结其区域地质资料及变形监测成果，利用组合预测思路开展滑坡发展趋势评价，以期为其防治提供一定的理论指导。

1 基本原理

1.1 预测思路初探

目前，常用的预测方法主要包含单项预测和组合预测，前者是利用单个模型进行预测，而后者则是基于多个单项模型，通过相应组合方法求得组合预测值，两者具体优缺点如下：

单项预测模型的优点主要是操作简单，利于模型构建及推广应用，但其缺点也较为明显，即单项预测模型难以完全刻画滑坡变形特征，加之其方法单一，预测结果的偶然性较大；为提升其预测精度，常采用参数递进优化等方法来保证模型参数的最优性，具有一定的效果。

组合预测是基于多种方法基础上构建的，能有效避免单项预测模型的偶然性，所得预测结果具有较高的稳定性，但其预测过程相较复杂，不利于推广应用。

由于计算机技术的快速发展，使得组合预测思路已发展成为目前的研究热点，且为保证本文预测精度及稳定性，提出利用组合思路来实现滑坡变形预测。但是，根据文献[6-9]的研究成果，传统组合预测存在一定不足：

① 未重视单项模型的预测效果。单项模型是组合预测模型构建的基础，其预测精度直接关系后续组合预测效果，但在传统组合预测过程中，重心多偏向于组合方法的构建，未重视单项模型的预测精度，存在一定不足。

② 未考虑训练样本与预测节点间距离对预测结果的影响。据文献[8]，训练样本与预测节点间的距离对预测效果具有明显影响，距离越近，其相关性相对越大，进而对预测节点的贡献值或新鲜程度也应越大；反之，则具有相对更小的贡献值或新鲜程度。在以往滑坡变形预测中，均较少涉及该方面研究，兹待解决。

③ 缺乏局部组合思路与全局组合思路的结合研究。在以往组合方法确定过程中，局部组合和全局组合多是单独考虑，未涉及两者的结合研究，使得组合方式存在一定不足。

概言之，组合预测具有其优越性，已发展成为主流研究方向，但其理论存在一定不足，仍待进一步优化研究。

1.2 组合预测过程的优化处理

1.2.1 单项预测模型的优化处理

在单项模型的优化处理过程中，需先对单项模型进行筛选，即不能随意选定单项模型，且单项模型的选定原则应具有普适性和互补性；据文献[10-12]研究成果，极限学习机(extreme learning machine，ELM)、支持向量机(support vector machine，SVM)和灰色GM(1,1)模型已被广泛应用于滑坡变形预测中，具有较强的普适性，且三种模型间具有一定的互补性。因此，本文将上述三种模型作为组合预测的单项模型。

同时，如前所述，为提升单项模型的预测精度，多采用参数优化处理来保证单项模型的预测精度，进而本文也利用该思路进行优化处理，并将各单项模型的优化处理详述如下：

① ELM模型的优化处理。ELM模型的缺点主要是隐层节点数的主观性及连接权值与阈值的随机性太强，并鉴于果蝇算法(fruit fly optimization algorithm, FOA)的全局优化能力，利用其实现ELM模型的参数优化。

② SVM模型的优化处理。SVM模型的待优化参数主要是核函数，其优化处理方法相对较多，常用如粒子群算法(particle swarm optimization，PSO)，因此，本文也利用PSO算法对SVM模型进行优化处理。

③ 灰色GM(1,1)模型的优化处理。在灰色GM(1,1)模型的预测过程中，初始值会对预测结果造成一定影响，需进行优化处理，且混合蛙跳算法(shuffled frog leading algorithm，SFLA)是一种新型智能优化算法，优化能力较强，进而利用其对灰色GM(1,1)模型进行优化处理。

通过上述优化处理，有效保证了单项模型的参数最优性，达到了单项模型优化处理的目的。

1.2.2 训练样本与预测节点间距离的优化处理

在训练样本与预测节点间距离的优化处理过程，先利用相对误差Ei(j)构建预测节点处的吻合度函数ci(j)：

ci(j)=1-Ei(j)，

(1)

式中，i为单项预测模型的序号；j为预测节点的序号。根据ci(j)可评价相应预测节点处的预测效果，吻合度值越大，说明预测效果相对越好；反之，预测效果相对越差。

其次，如前所述，训练样本与预测节点间的距离越近，其对预测节点的贡献值或新鲜程度相对越大；反之，贡献值或新鲜程度相对越小。因此，再引入新鲜度函数f(t)，其计算公式为

(2)

式中，t为训练样本与预测节点间的距离。据公式(2)，训练样本与预测节点间的距离越大，新鲜度函数f(t)值越小，这与其含义相符。

最后，再以ci(j)和f(t)为基础，构建考虑训练样本与预测节点间距离的综合评价函数li(j)t，其计算公式为

(3)

li(j)t不仅能反映训练样本与预测节点间距离对预测结果的影响，还能有效反映对应相应预测节点处的吻合度，具有较强的全面性。同时，li(j)越大，说明预测效果越好；反之，预测效果越差。

1.2.3 局部组合思路与全局组合思路结合的优化处理

首先，由于li(j)t主要用于相应预测节点处的评价，进而可利用其求解局部组合权值wJ(i)，求解公式如下：

(4)

式中，n为单项模型个数；N为训练样本与预测节点间的距离长度。

其次，考虑到局部组合权值已包含了预测精度评价，进而在全局组合权值wQ(i)构建过程中，侧重考虑预测结果的稳定性，将其求解公式表示为

(5)

式中，qi为对应单项模型预测结果的方差值倒数。

最后，前述已计算得到了wJ(i)和wQ(i)，需进一步将两类权值组合，以实现局部组合思路与全局组合思路结合的优化处理，且结合相关文献[11]研究成果，得出累乘叠加思路具有相对更优的组合效果，进而将wJ(i)和wQ(i)相乘，得到组合预测的基础评价指标m(i)为

m(i)=wJ(i)wQ(i),

(6)

m(i)值越大，说明单项模型的预测效果相对越优，进而对其进行归一化处理，所得归一化值wG(i)即可作为本文组合预测模型的最终组合权值，其求解公式为

(7)

通过上述逐步优化，有效克服了传统组合预测方法的不足，为滑坡变形预测奠定了较强的理论基础。

2 实例分析

2.1 工程概况

藕塘滑坡位于重庆奉节，距三峡大坝约177.00 km，纵向长度约1.80 km，宽度呈前宽后窄，平均宽度约0.85 km，面积约1.78 km2，平均厚度约51 m，体积为9×107m3，属特大型滑坡；结合现场调查，滑坡区具单斜顺向岸坡结构，地形起伏较大，地表呈阶状陡缓特征，斜坡一般坡度间于15°～40°，局部可达60°。

在地质构造方面，滑坡区无大型断裂构造，但受故陵向斜影响，区内节理裂隙较为发育，降低了岩体完整性。同时，在地层岩性方面，区内第四系主要以残坡积层、冲洪积层及滑坡堆积层为主，岩性为粉质黏和黏土，含有少量碎石，结构松散，厚度分布差异较大；下覆基岩主要为侏罗系砂泥岩互层，质软，遇水易软化，发育有软弱夹层。

在水文特征方面，滑坡区属亚热带季风气候，年均降雨量为1 148.1 mm，年最大降雨量达1 636.5 mm，全年集中降雨时段为5月至9月。同时，区内地表水以长江水系为主，库水位于145～175 m波动，并在强降雨条件下，坡面易形成地表径流；地下水则主要包含孔隙水和裂隙水两类，前者多赋存于第四系土层孔隙中，而后者多赋存于下覆基岩裂隙中，两者多接受降雨补给。

2.2 滑坡发展趋势分析

2.2.1 变形迹象分析

藕塘滑坡近期变形迹象主要开始于2008年，其变形特征主要是前缘滑体出现了若干地表裂缝；后期历年具有不同程度的变形；至2012年，前缘变迹象趋于减弱，地表变形发展至滑坡中部公路一带；其后，滑坡前缘岸坡历年垮塌，地表变形也随时发生。

为充分掌握藕塘滑坡发展趋势，对其进行了变形监测，其中，主滑面的地层条件及监测点布置如图1所示。

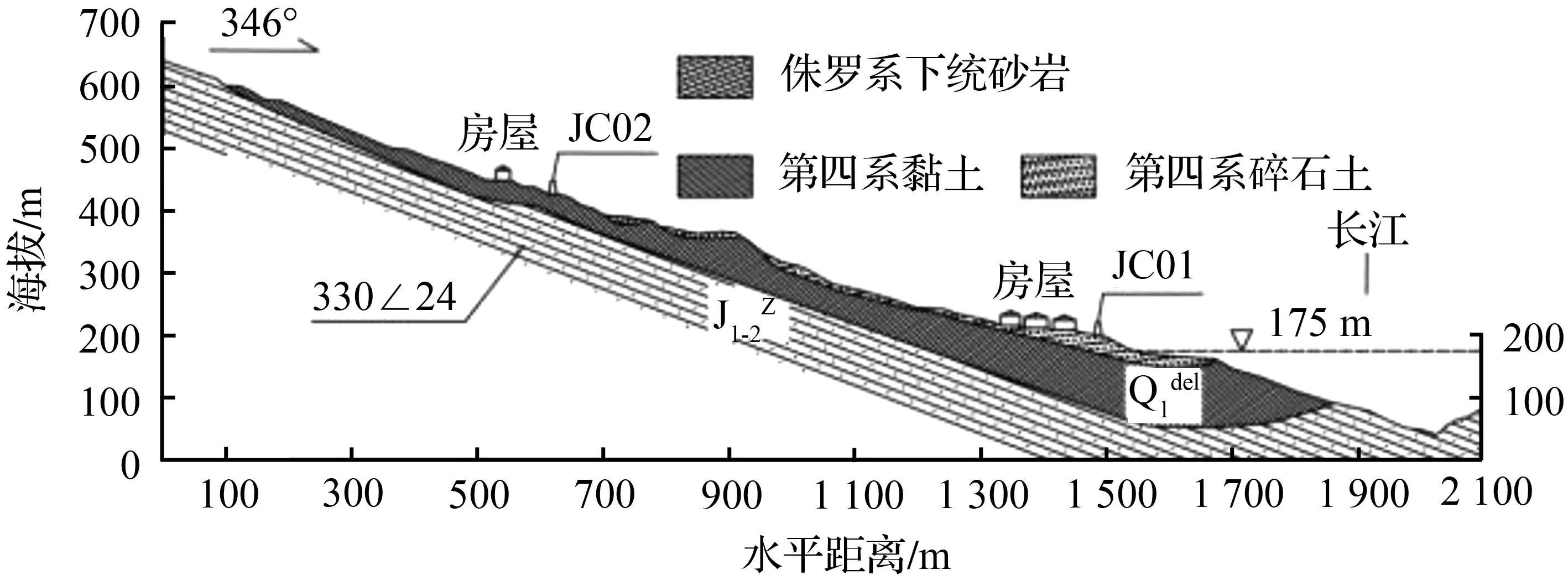
图1 主滑面的地层条件及监测点布置

在监测过程中，监测频率为1次/月，得两监测点(JC01、JC02)。2010年12月至2014年8月藕塘滑坡面变形曲线如图2所示。由图2可见，藕塘滑坡主滑面上的变形具持续增加趋势，一方面，进一步说明对藕塘滑坡进行研究的必要性；另一方面，说明滑坡稳定性趋于不利方向发展，将主滑面两监测点的监测成果作为后续滑坡发展趋势分析的数据来源是可行的。

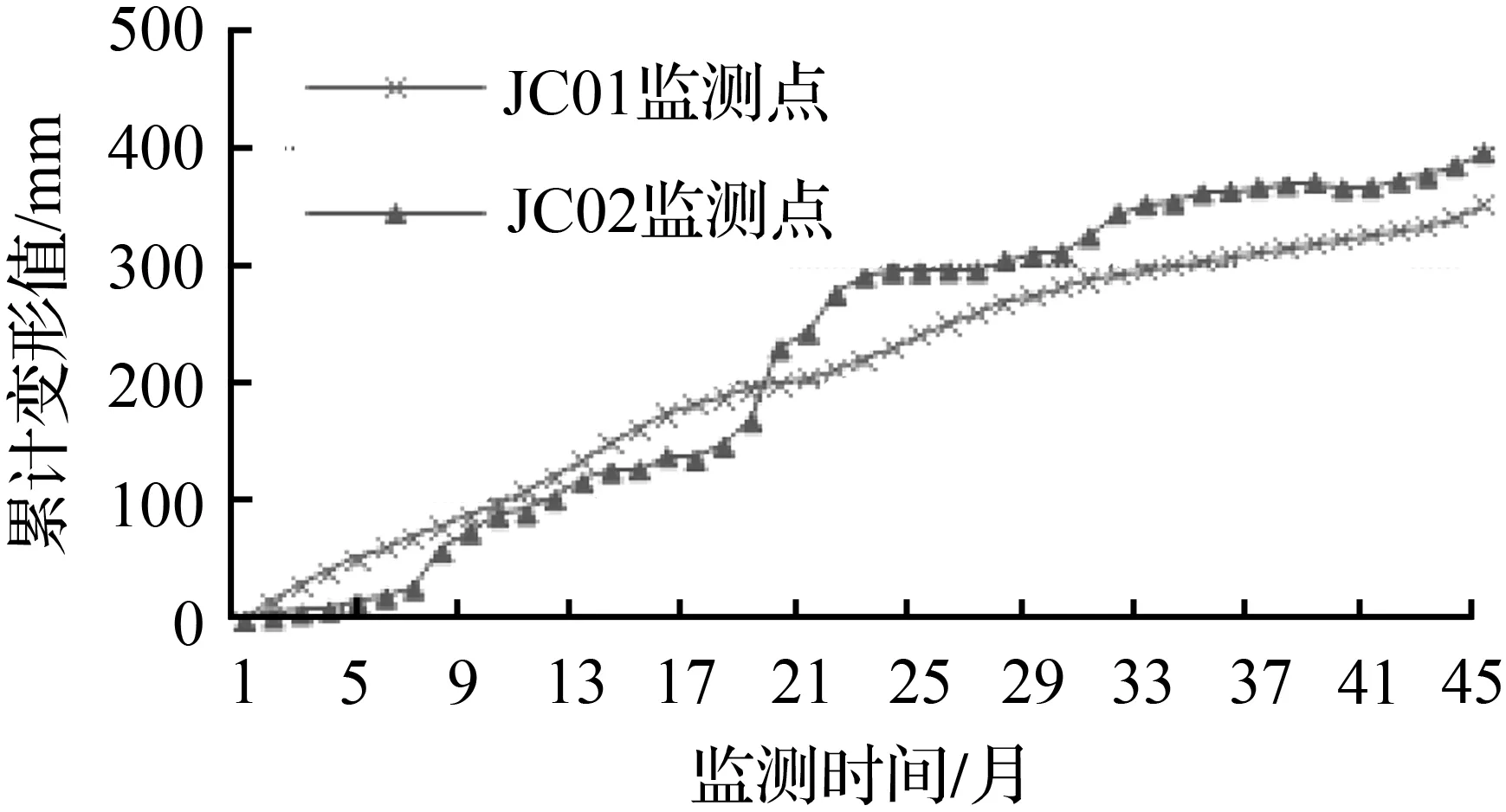
图2 藕塘滑坡主滑面变形曲线

2.2.2 变形预测分析

该节重点利用组合预测思路实现滑坡变形预测分析，旨在确定滑坡变形发展趋势；在预测过程中，以1～39周期为训练样本，40～45周期为验证样本，外推预测4个周期，且为佐证本文预测过程的有效性，先以JC01监测点为例，进行组合预测效果的初步验证，即详述不同组合阶段的预测效果，再以JC02监测点和其他传统预测方法进行对比预测，实现组合预测思路的可靠性验证。

① 初步预测验证分析

在组合预测过程中，先利用相应优化算法对各单项模型进行优化处理，得单项模型优化前后的预测结果对比见表1。由表1可知，在对应单项模型的相应验证节点处，通过单项模型的优化处理，预测结果的相对误差值均出现了不同程度的减小，且三类单项模型优化后的平均相对误差值也均出现减小，得出经单项模型的优化处理，能有效提高预测精度；但是，通过优化处理，三类单项模型的训练时间均出现了增加，其原因应是优化过程增加了网络结果的复杂性，进而增加了训练时间，鉴于训练时间均较短，属可接受范围，认为该文单项模型的优化处理是有效的。

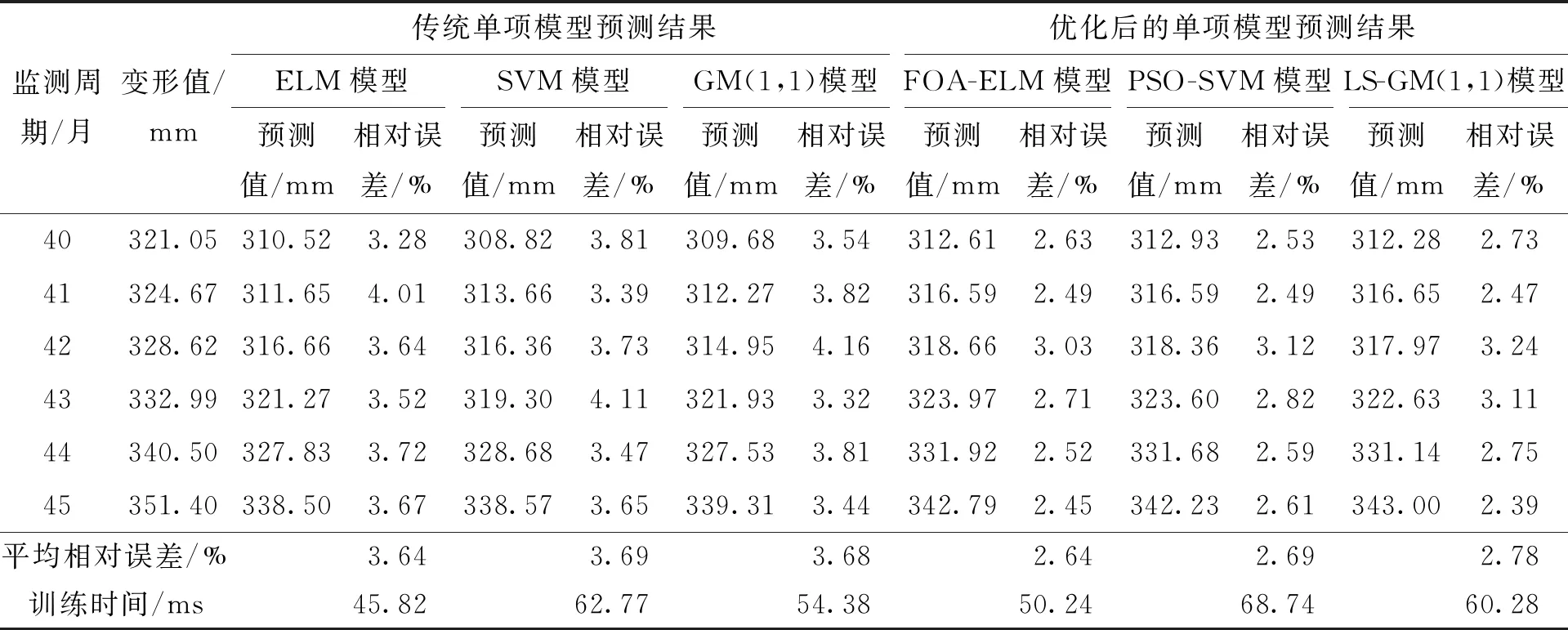
表1 单项模型优化前后的预测结果对比

其次，为验证不同组合阶段的预测效果，本文将不同组合阶段进行模型划分，即：

模型1：组合过程仅考虑局部组合权值。

模型2：组合过程仅考虑全局组合权值。

模型3：组合过程仅考虑“吻合度+全局组合权值”。

模型4：综合考虑了局部组合权值和全局组合权值，包含了该文组合思路的所有过程。

根据上述模型结构，得不同组合模型的预测结果见表2。

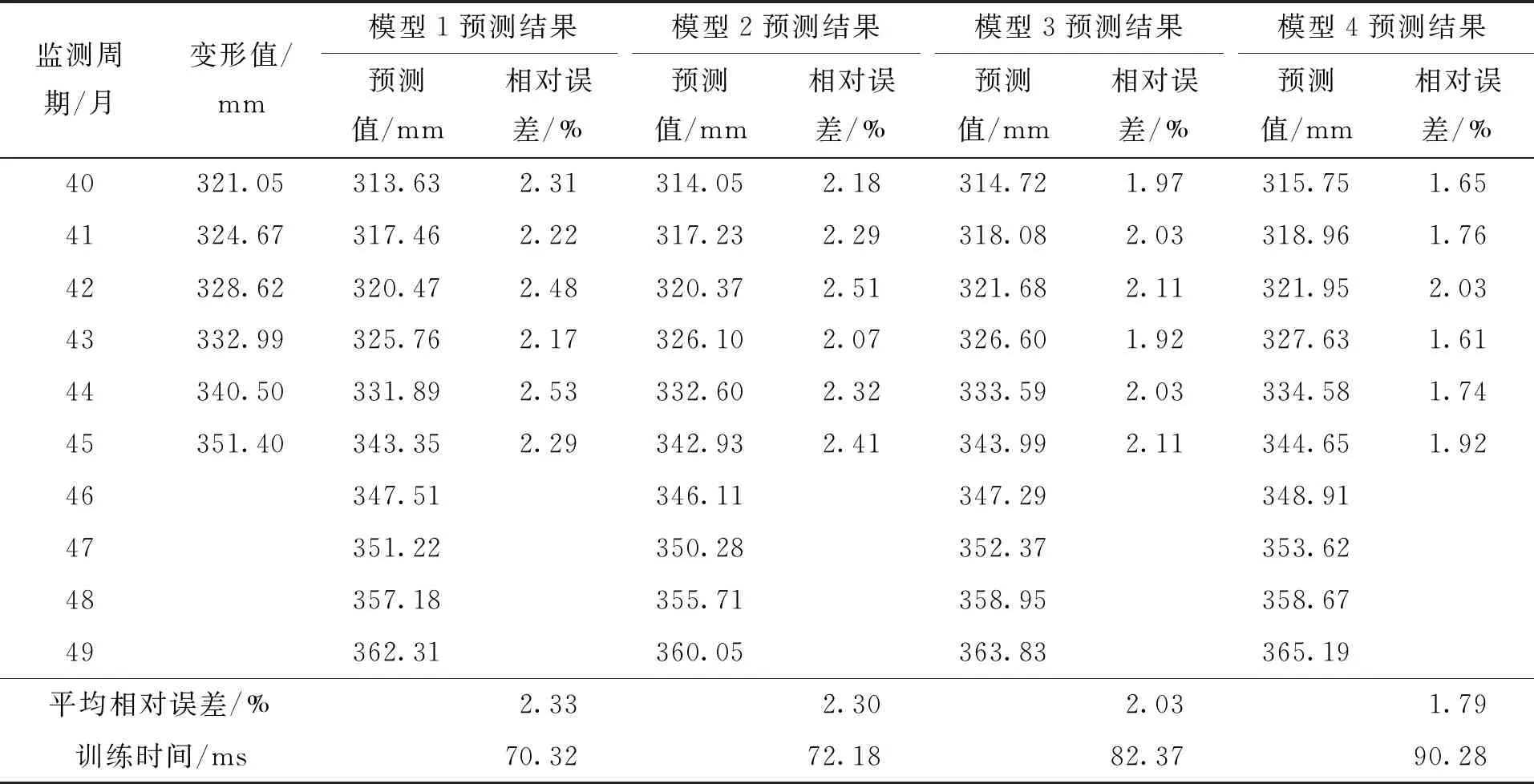
表2 不同组合模型的预测结果

由表2可见，不同组合模型的预测效果存在明显差异，模型1和模型2的预测效果相当，但均不及后续两个模型的预测效果，说明仅从单一组合角度出发难以保证预测精度；同时，对比四类组合模型的预测结果，模型4的平均相对误差值最小，仅为1.79%，说明其预测精度相对最高，但其训练时间也相对最大，说明通过该文递进组合能不断提高预测精度，但会增加训练时间，增加量也属可接受范围。另外，根据外推预测，得出JC01监测点的后期变形仍会进一步增加，且增加速率仍较大。

② 可靠性验证分析

前述已利用JC01监测点为例初步验证了该文组合思路的有效性，再利用JC02监测点和多种传统神经网络模型进行可靠性验证分析。先对JC02监测点进行预测分析，结果见表3。由表3可见，JC02监测点预测结果的最大、最小相对误差分别为2.07%和1.68%，平均相对误差为1.83%，具有较高的预测精度，进一步验证了本文组合思路的预测精度；同时，在训练时间方面，所花时间与JC01监测点相近，也属可接受范围，也验证了本文组合模型的稳定性相对较强。根据JC02监测点的外推预测结果，得其后期变形也会进一步增加，且增加速率也较大。

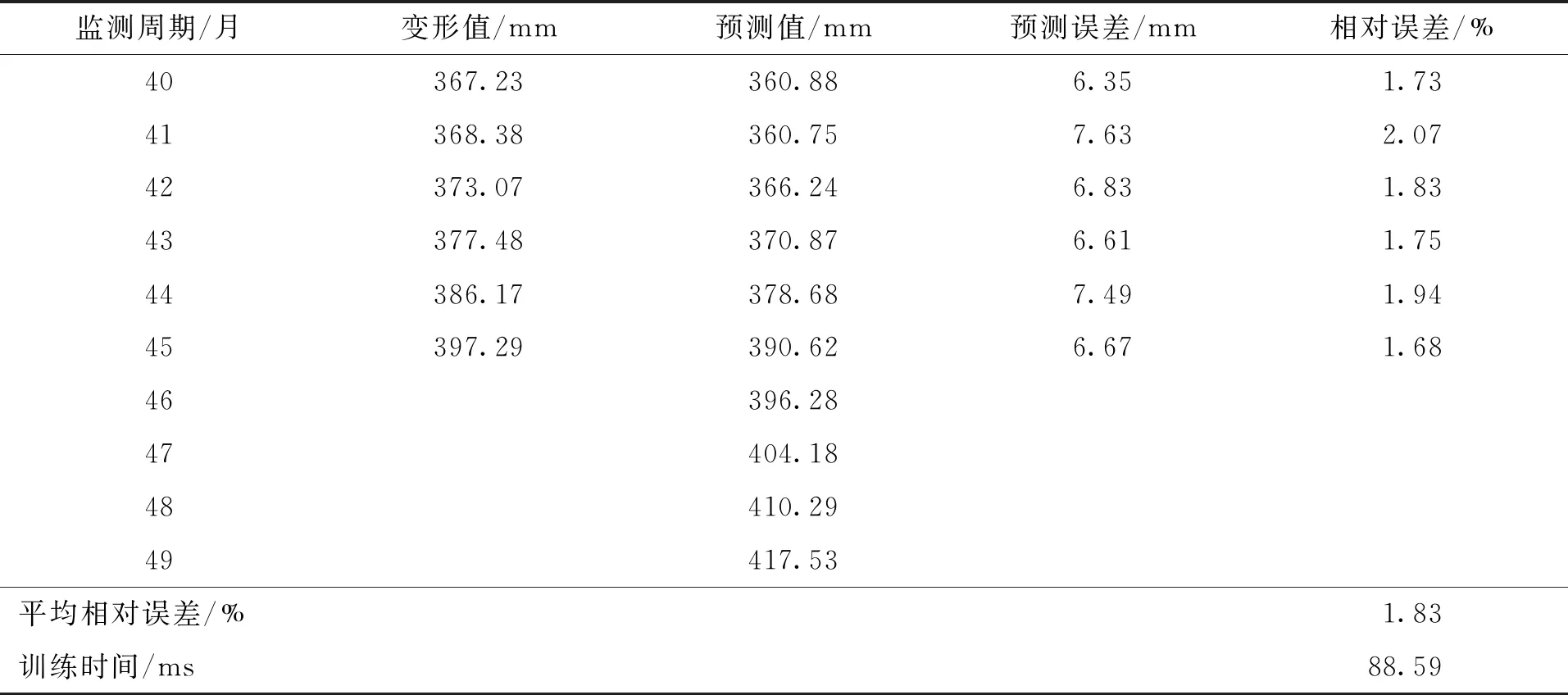
表3 JC02监测点的预测结果

其次，再利用传统RBF神经网络和传统BP神经网络对两监测点进行预测分析，并将其结果与本文组合预测结果对比(表4)。由表4可见，在相应监测点，该文预测模型均明显优于两种传统预测模型，不仅具有相对更高的预测精度，还具有相对更短的训练时间，再次验证了本文预测模型的效果及优越性。

表4 传统预测模型与该文预测模型的对比

结合上述变形预测结果，得出藕塘滑坡变形趋势性虽具有一定程度的减弱，但滑坡变形始终具上升趋势，且增加速率相对较大。

3 结论

通过对藕塘滑坡的发展趋势评价，得出本文组合预测思路具有较高的预测精度，相较于传统预测模型具有较为明显的优越性，且其预测结果显示滑坡变形具上升趋势，增加速率相对较大，充分说明开展该滑坡研究的必要性，且应采取切实措施，避免成灾损失。