自然邻居密度极值聚类算法

张忠林，赵 昱，闫光辉

兰州交通大学 电子与信息工程学院，兰州 730000

数据聚类把数据对象按照不同属性分割成确定数目的同质子集，每个同质子集贴上属性标签后称之为类簇。对于任何一个类簇满足簇内数据对象特征相似，簇间数据对象特征差异较大的条件[1]。聚类概念已被引入到多个研究领域之中，例如：智能算法改进、大数据分析、模式检测、神经网络等[2]。聚类算法发展过程中提出了许多经典算法，如基于划分思想k-means算法[3]、基于层次思想EM算法[4]、基于密度思想DBSCAN、RNNDBSCAN算法[5-6]，基于网格思想CLIQUE算法[7]、基于模糊思想FCM算法[8]。

随着对数据集深入研究发现密度峰值是数据集的一个重要属性，因此2014年Rodriguez等[9]提出基于密度峰值算法（clustering by fast search and find of density peaks，DPC），DPC算法迭代过程中人工调参少，可以发现任意非球状簇并且敏感数据集中的噪声点。但是DPC算法也存在三个不足[10]：（1）预先选取的截断距离具有一定随机性和经验性，选取的截断距离直接影响聚类结果的好坏；（2）计算局部密度时忽略数据分布情况，当簇间的数据稀疏程度相差较大时，即使设定合理参数也得不到理想聚类效果；（3）数据对象间相似性度量仅采用欧氏距离模型，在高维数据集中导致度量结果不准确，并且随着数据集规模递增，每迭代一次相似性计算次数为n(n-1)2，导致算法时间复杂度为O(n2)影响算法效率。

DPC算法存在人工选择的随机性和数据间度量准则的不准确性。对上述两个问题提出了多种改进方法，Du等[11]提出了k近邻方法，利用k-近邻概念定义截断距离和局部密度，该方法根据数据集特征能够生成合理的截断距离，在新的截断距离下计算的局部密度更符合数据集的真实分布，引入决策图将决策点选取可视化。Gou等[12]把数据对象的k-最近邻引入图G中，对于任意数据对象若存在数据对象是其最近邻，则在这两点之间生成一条边赋予对应的权值，遍历图用权值来定义局部密度。Jin等[13]引入自然邻居概念，采用树的遍历检索最近邻，来消除对于参数k的敏感问题。Wang等[14]提出了基于极值的聚类方法剔除离群点，在局部范围内采用合并运算找到近邻最多的点设置为聚类中心，以此聚类中心为基础完成聚类。

基于上述研究，本文针对密度峰值算法的不足：（1）当样本数据集密度差异较大时，低密度区域聚类中心比高密度区域聚类中心难以发现，导致聚类结果不准确；（2）当聚类更稀疏时，一个数据对象被识别成离群点概率增加；为了解决上述的两个问题，提出了自然邻居密度极值聚类算法（Natural Neighbor Density Extremum Clustering algorithm，NN-DEC）。该算法以密度极值作为聚类中心选择标准，更加准确和全面地选取数据集聚类中心。首先调用自然邻居搜索算法，迭代有限次后数据集形成自然稳定状态，在该状态下分割出数据对象的自然邻居；其次将处理后数据集导入密度距离自适应模型，生成数据对象局部密度；然后，计算数据对象连通值，在使用连通值将数据集划分成高低密度区域和离群点，引入密度极值函数找出不同区域聚类中心点；最后，将不同区域内未被分配数据对象，划分到离其最近的聚类中心所在簇中合并聚类结果。

1 相关工作

表1为文章所定义数据符号和算法缩写摘要。

表1 符号摘要Table 1 Summary of notations

1.1 DPC算法

DPC算法聚类中心选取条件：（1）簇中心点为局部密度最高的点，周围任何一点局部密度都低于簇中心点；（2）对于任意簇中心点比它密度更高的局部密度峰值点，在数据集中与其分布的距离较远。DPC算法核心需要计算xi的局部密度ρi以及最近距离δi。局部密度ρi计算如公式（1）所示：

DPC算法另一种计算局部密度的方法采用高斯核定义计算，如公式（3）所示：

使用高斯核计算数据对象的局部密度，ρi等于截断距离dc内数据对象的个数和。

δi计算方法如公式（4）所示：

DPC算法将局部密度ρi和距离δi归一化处理后，用做标准量引入到决策图中，在决策图中选定ρ和δ标准值。DPC算法伪代码[15]如算法1所示：数据样本为N，算法的时间复杂度为O(N)。

算法1DPC(ρ,d)

Input：局部密度ρ，距离矩阵d

1.2 密度自适应距离度量

如图1所示，以欧式距离度量数据对象a和b之间的相似性，因距离较近则两个数据对象相似性较高，可划分到同一个簇中。但在数据集实际分布中a和c处在同一簇中，因此欧氏距离度量准则在该数据集中的度量误差较大，同时不满足上述聚类假设中特征交叉相似性。

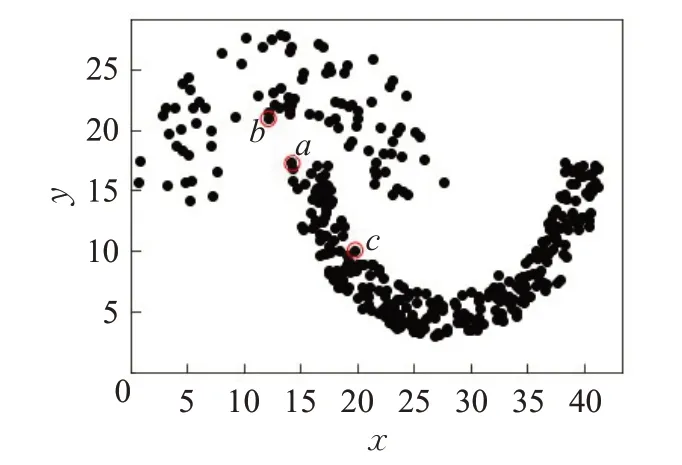
图1 合成数据集Fig.1 Synthetic datasets

基于上述分析应在环状和密度差异较大数据集中，引入一种新的密度自适应距离度量方法。文献[16]提出一种有效的密度自适应距离度量模型，将一个数据集分布映射到一个二维椭圆模型中，建立椭圆二维空间，度量两个数据对象之间相似性度量，椭圆长轴和短轴参数将参与到运算过程中。

定义A={a1,a2,…,an}，B={b1,b2,…,bn}，自适应距离度量如公式（5）所示：

其中，wl和ws计算如公式（6）所示：

其中，wij1和wij2计算如公式（7）所示：

本文中采用高斯核方式进行局部密度计算，对于每一个数据对象都可以求出它在数据集中的局部密度ρi，密度自适应距离度量方法如公式（8）所示：

1.3 锚点选取方法

数据集中固定的点称之为锚点，引入基于锚点的聚类[17]，计算每一个成为聚类中心点的最小损耗值，利用损耗值来优化聚类中心的选取。锚点选取如公式（9）所示：

f(xj)计算由公式（10）所示：

指示函数值为1表示该数据点可以作为锚点，值为0表示该数据点不能作为锚点。

1.4 高低密度区域划分和离群点检测

定义1（离群点[18]）观察一组数据对象，存在异于这组观察值的数据对象被称为数据集中的离群点。

定义2（相似性度量）定义P={p1,p2,…,pn}和S={s1,s2,…,sn}，P和S属性之间采用余弦相似性度量准则，如公式（11）所示：

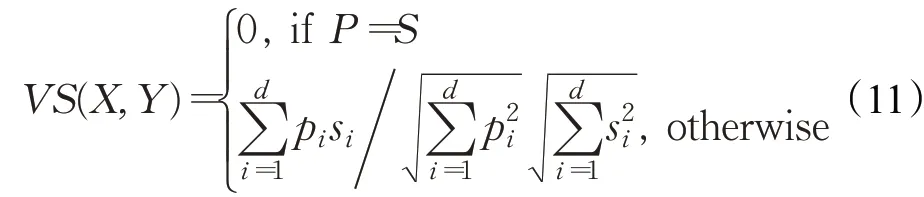
数据集中所有向量计算后会生成一个余弦相似性矩阵Simn×n，n为数据集大小。矩阵中的每一项Sim[i,j]对应于xi和xj之间相似性值，使用相似性矩阵构建相互邻居图，问题就转换成了如何在图上找到孤立的点。假设该图连通子图集合中存在孤立的点，则该点就可以称之为数据集中的离群点。

节点u的连通值[19]c(u)会随着迭代次数t收敛于一个稳定的值，如公式（12）所示：

初始化每一个节点的连通值c0(vi)=1n(i:1-n)。

S称之为转移矩阵，如公式（14）所示：

相似矩阵标准化可以使得：（1）转移矩阵中的每一行的求和的值为1；（2）符合马尔可夫链的基本性质；根据连通值的大小找到数据集中的高低密度区域和离群点。

算法2Detection(X,T)

Input：数据集X={x1,x2,…,xn}，密度阈值T

Output：X_high，X_low，Outlies

算法2中主要是对数据集中每个元素连通值计算，假设数据集大小为n，则计算连通值时间复杂度为O(n2)，转移矩阵S计算时间复杂度也为O(n2)，算法2主要包括连通值和转移矩阵计算，因此时间复杂度为O(n2)。

1.5 自然邻居

自然邻居[20]是一种无参的近邻概念，提出的目的是解决k-最近邻[21-22]中参数选择问题。

定义3（自然稳定结构[23]）xi存在邻居为xj，同时xj也存在邻居为xi，若满足上述条件则xj是xi自然邻居；若数据集任意数据对象存在至少一个自然邻居，数据集就形成了自然稳定结构（Natural Stable Structure，NSS）。

定义4（k-最近邻[24]）数据对象xi与数据集中其他数据对象的欧氏距离，小于设定阈值的所有点集合，通过上述集合生成自然邻居集合（Natural Neighborhood Set，NNS）。

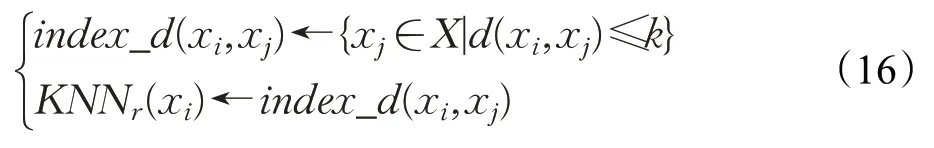
定义5（自然特征值[25]）自然邻居特征值（Natural Neighbor Eigenvalue，NNE）λ是在搜索自然邻居过程中，当数据的形成NSS结构时所迭代的次数。

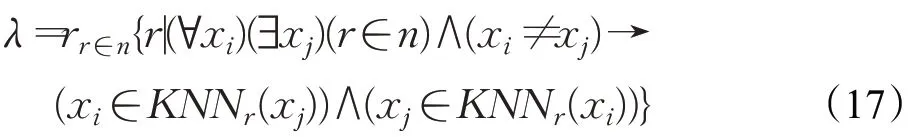
定义6（自然邻居[25]）自然邻居（Natural Neighbor，NaN）在集合概念下定义如公式（18）所示：

如图2，对比了自然稳定状态下数据对象之间的关系和k近邻下数据对象之间的关系。

图2 自然邻居和k最近邻对比Fig.2 Comparison of natural neighbors and k-nearest neighbors

基于上述公式的分析，给出自然邻居搜索算法基本思想：首先要寻找到每一个数据对象的k-最近邻，根据k-最近邻结果构造相互邻居图。算法迭代终止条件：（1）不存在最近邻数据对象时；（2）迭代次数大于等于自然邻居个数减去迭代次数开方时。自然邻居搜索算法（Natural Neighbor Search Algorithm，NaNSA）如算法3所示：

算法3NaNSA(X)

Input：数据集X={x1,x2,…,xn}

Output：自然邻居个数num，相互邻居图G，自然特征值λ

算法3的时间复杂度分析：假定数据对象个数为n，算法时间消耗主要在构建KD树数据结构上，构建KD树的时间复杂度为O(nlbn)。由于数据对象个数n是有限的，因此算法时间复杂度为O(nlbn)。

2 NN-DEC算法

2.1 聚类中心确定

根据文献[26]提出极值理论，极值描述现象是“不平均”分布，聚焦的是高分位数而不是数据集整体的统计数据。例如，样本均方差、样本期望、样本离差平方和等。

密度差异较大的数据集对低密度区域聚类中心选取存在一定误差，会导致聚类结果不准确，因此引入极值概念来解决上述出现的问题。本文采用密度极值目标函数计算每一个数据对象局部密度极值，采用椭圆模型处理后，使局部密度更加贴合数据集的真实分布。

自然邻居搜索算法自适应得到数据对象自然邻居，自适应搜索过程中消除了对于截断距离dc的敏感问题。对得到自然邻居数据对象计算局部密度，根据数据对象之间欧式距离选择聚类中心存在误差，因此引入上文提出密度自适应距离方法，选择高低密度区域聚类中心。

为了提升算法效率调整因子采用线性方式计算wij=θwij1+(1-θ)wij2。θ计算取决于wij1和wij2，调整因子计算方式如公式（19）所示：

因此自然稳定状态下xi局部密度计算公式，如公式（21）所示：

采用上文提到过的密度自适应距离度量方法，对数据对象局部密度计算。上述方法当数据集为NSS状态时计算每一个数据对象局部密度。

密度在一个数据集中分布是不平衡，因此会存在高密度区域和低密度区域，选取聚类中心时需要设置一个合理阈值，区分出聚类中心点和非聚类中心点。

归一化采用最小最大标准化处理（Min-Max Normalization）如公式（22）所示：

使用上述归一化处理可以将密度和距离范围控制到[0,1]范围之内。计算出ρi如公式（23）所示：

密度和距离归一化处理后，如图3所示。

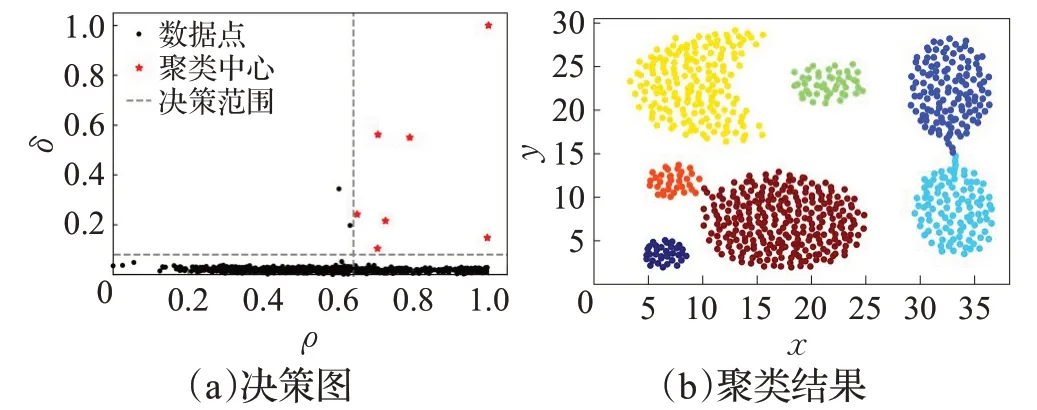
图3 决策图和聚类结果Fig.3 Decision graph and clustering results

从上述决策图看出在决策范围中出现了7个聚类中心点，这些点可以作为聚类中心。体现在图3（b）中Aggregation聚类结果图，标准化后聚类中心选择更加准确，边界区分明显聚类效果提升。

本文设定φ(x)计算采用均方根公式，将其引入到聚类中心识别函数中，如公式（24）所示：

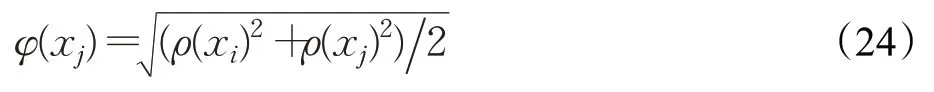
引入上文提到锚点选取方法，构造一个聚类中心识别函数H，如公式（25）所示：

其中，密度自适应距离度量过程中，将损益值取均方根保证算法在迭代过程中函数损益值不会出现负值。上述公式第二部分cosρ(xj)引入密度对于聚类中心选择的影响，公式（21）对于低密度区域聚类中心选择误差较大，在此基础上用极值来寻找聚类中心。

对公式（25）中密度ρi求导可得：

对于函数H进行求导时，将数据集每一个数据对象密度看作变量，数据对象xi密度在求导过成中当作常量。公式（25）中f(xj)判断该数据对象是否为锚点指示，若是锚点则取值为1，若不是则取值为0；公式（26）求导后得到结果为公式（27）所示，其中将ρi替换后并且去掉集合符号得到一个密度极值函数，如公式（27）所示：

其中，x代表数据对象密度，密度定义在[0,1]，函数H′中幂函数增幅是大于正弦函数增幅，根据导函数定义在定义域范围内大于零，得出该导函数对应的原函数是单调递增，对于局部来说函数值越大，代表这个点周围数据点分布是更加密集，说明这个数据对象在局部范围内具有更高的密度。使用极值方法可以在高低密度区域中准确识别到聚类中心点。

2.2 高低密度区域聚类

根据2.1节按照统一密度阈值去选取聚类中心，低密度区域聚类中心选取会存在误差，针对上述问题构建马尔可夫模型，使用模型生成相互邻居图，利用图上节点连通值去区分低密度和高密度区域，并且剔除掉离群点，进而对两个区域分别进行聚类。

首先利用公式（11）计算每一个数据对象与其他剩余数据对象之间的VS值，采用这些值生成一个余弦相似性矩阵Simn×n，其中矩阵中每一项sim[i,j]代表，数据对象xi和数据对象xj之间VS值；对Simn×n每一行进行归一化处理得到转移矩阵，得到转移矩阵后初始化每一个数据对象连通值c(u)，在每一次迭代中使用公式（12）更新当前每一个数据对象c(u)值；当连续两次迭代中，数据对象连通值不再发生变化说明节点连通值稳定，然后将每一个数据对象连通值进行降序排列。根据文献[19]提出的模型设定阈值T，区分出高低密度区域和离群点，如果一个数据对象连通值c(u)等于0，则说明该数据点为这个数据集中的离群点。

区分出高密度和低密度区域后，两个区域分别进行聚类，高密度区域聚类，首先剔除离群点，再使用密度自适应距离方法计算数据对象局部密度极值，对比密度极值，大于所设定的密度阈值点归入聚类中心点集合，高密度区域非聚类中心点较多，可以采用最近邻原则将剩余点归并到最近的簇中。在低密度区域，将每一个数据对象密度带入公式（27）计算密度极值，当大于设置密度阈值时，将该点划入聚类中心集合之中，因为在低密度区域中剩余数据量较少，将集合中非聚类中心点使用k-means算法完成聚类，各自完成聚类后合并两个区域的聚类结果。

基于上述分析，给出NN-DEC算法基本思想：首先，引入自然邻居概念消除了对近邻参数k的敏感问题，采用密度自适应距离方法来计算数据对象局部密度。其次，构建锚点和密度极值函数筛选聚类中心，计算每一个数据对象连通值，根据连通值排序将数据集拆分成高密度区域和低密度区域，分别计算每个区域内数据对象密度极值，迭代对比将数据集分成聚类中心点集合和非聚类中心点集合。最后将非聚类中心点集合，按近邻原则归并到距离其最近的聚类中心所在簇中。NN-DEC算法伪代码如算法4所示：

算法4NN-DEC(X)

Input：数据集X=(x1,x2,…,xn)

Output：聚类结果CL

设数据集中数据样本个数为n，首先，获得自然邻居的时间复杂度为O(nlbn)，在自然稳定态下计算局部密度时间复杂度为O(n2)。在进行聚类之前需要将数据集分成不同的区域，采用连通值构建相互邻居图时间复杂度小于O(n2)，离群点检测和高低密度区域聚类，时间复杂度均小于O(n2)，综上所述算法4时间复杂度为O(n2)。

3 实验结果与分析

为了验证NN-DEC算法在不同数据集上的聚类效果，分别在人工合成数据集和真实数据集上运行算法。合成数据集包括不同规模和不同形状的数据集，用于验证算法处理不同形状簇的效果；真实数据集：UCI公共数据集，数据集稀疏程度差异较大来验证算法聚类效果。通过与基于聚类中心的K-means算法[3]、基于密度的DBSCAN算法[5]、DPC算法[9]、基于K近邻优化的KNN-DPC算法[11]、基于密度极值的EC算法[14]、基于自然近邻密度极值优化的NNDP算法[13]进行各项指标的对比。

实验环境：Operating System Win10 64；Inter®Core™i5-10210U CPU＠1.60 GHz 2.11 GHz处理器，16.00 GB RAM。所有代码采用Python语言实现。

聚类评价指标为标准互信息[27]（Normalized Mutual Information，NMI）、F值[1]（F-Measure）、聚类准确率[27]（Clustering Accuracy，CA）以此来判断全局聚类准确性。其中NMI、F值和CA取值范围为[0,1]，值越接近1表示在该数据集上聚类效果明显。

3.1 合成数据集实验结果分析

本节中采用7个合成数据集进行实验，各类数据集的基本属性如表2所示。选取表2中四个数据集对比NN-DEC和K近邻算法，聚类中心点和非聚类中心点之间的紧凑程度如图4所示。选取表2中四个人工数据集对比NN-DEC算法和DPC算法，聚类效果如图5所示。

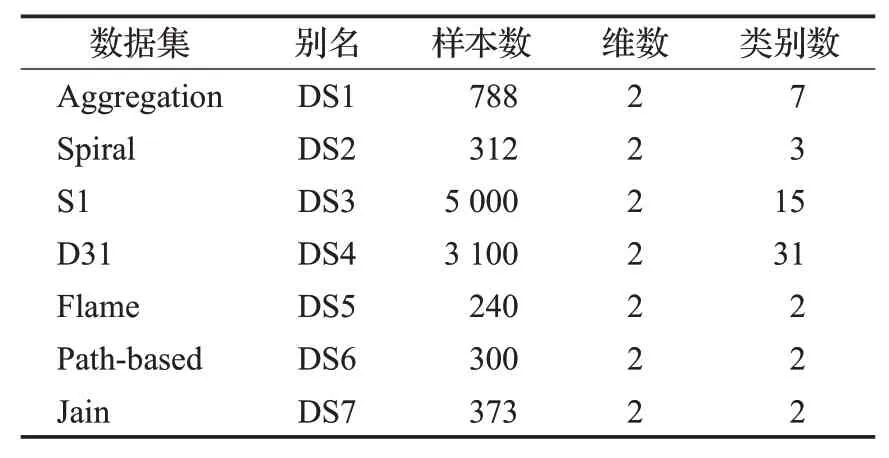
表2 合成数据集Table 2 Synthetic datasets

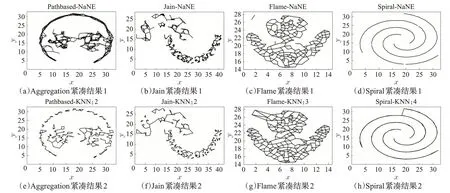
图4 NN-DEC算法在Aggregation、Jain、Flame、Spiral上紧凑结果Fig.4 Compact results of NN-DEC algorithm on Aggregation，Jain，Flame，Spiral

图5 NN-DEC和DPC算法在Aggregation、S1、Flame、Spiral上聚类结果Fig.5 NN-DEC and DPC algorithm clustering results on Aggregation，S1，Flame，Spiral

在图4中可以看出本文提出的算法，对于聚类中心和非聚类中心之间的紧凑程度表达更好，在Spiral数据集上NN-DEC算法的边界紧凑效果更加明显。对于Jain数据集，本文算法在聚类的紧凑程度好于DPC算法。

图5中前4个子图为NN-DEC算法聚类效果，后4个子图为DPC算法聚类效果。从图5中可以看出，在Flame合成数据集上，由于簇之间分布距离较近密度分布差异不均衡，因此在DPC算法进行聚类时导致聚类结果不准确，而采用NN-DEC算法进行聚类时，剔除了离群点影响，密度分布不均衡有更好的聚类结果，并且在其他合成数据集上具有较好聚类分布。其余几个数据集上来看NN-DEC算法聚类结果的边界更清晰，准确度更高，聚类效果更加明显。接下来分别在合成数据集上计算CA、NMI、F值。对上述对比聚类算法计算各指标值，结果如表3所示。

表3中展示了NN-DEC算法与对比的NNDP算法、EC算法、KNN-DPC算法、DPC算法、DBSCAN算法、Kmeans算法在合成数据集上三种评价指标，可以看出除了Flame数据集，其他六个数据集上性能都优于所对比的算法。具体分析：在Aggregation数据集上因为数据分布广且密度分布不均匀，因此NN-DEC算法在上面聚类效果是最佳的，NNDP算法的性能要优于EC算法，因为数据点密度分布较为均匀，EC算法在Aggregation数据集上性能也是较好的。S1数据集类别数较多、每个类之间密度差异较大、类之间距离较远，因此NNDEC算法在S1数据上性能优于NNDP算法。Pathbased数据集数据分布相对集中密度分布较均匀，因此NN-DEC算法在该数据集上密度计算准确，聚类效果优于其他对比聚类算法。Spiral是一个环状数据分布，数据间稀疏程度适中，由于数据间稠密程度均匀，NNDP、KNN-DPC、DPC、DBCSCAN算法和NN-DEC算法在该数据集上聚类性能相当。Flame数据集上类别较少密度分布相对集中，EC算法在该数据集上性能要优于NN-DEC算法。综上所述说明NN-DEC算法在处理密度差异较大数据上具有不错的效果。

采用折线图方式来直观表达NN-DEC算法NMI值，整体上优于其他对比算法，如图6。

从图6中可以看出NN-DEC算法NMI值优于其他对比算法，在DS6数据集上NN-DEC算法聚类结果明显优于EC算法。

3.2 UCI数据集实验结果分析

本节选取6个数据稀疏程度较大UCI真实数据集进行实验。计算NN-DEC算法和对比算法，在真实数据集上的各个指标值。如表4所示，所选取UCI数据集都为常见代表数据集，其中Waveform数据集为数据密度分布较密集、不均匀程度较大，具有代表性的一类数据。

表3 各聚类算法在合成数据集上的评价指标对比Table 3 Comparison of evaluation metrics of various clustering algorithms on synthetic data sets

图6 算法在DS1～DS7上NMI值Fig.6 Algorithm NMI values on DS1～DS7

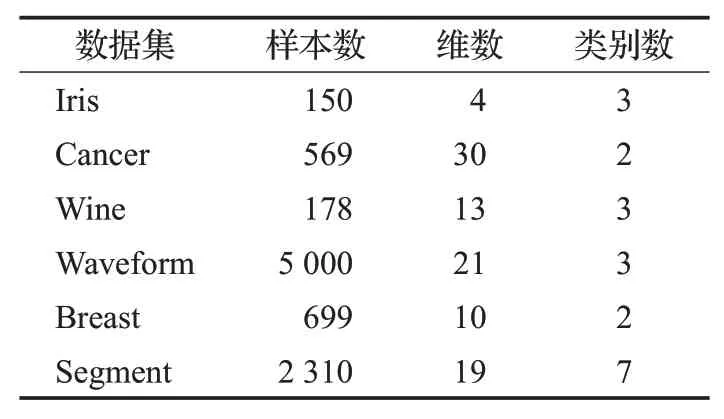
表4 UCI数据集Table 4 UCI Datasets

表5中计算了CA、NMI、F值三个聚类指标，并给出了NN-DEC算法和其他六个算法，在六个UCI公共数据集上的聚类指标结果。从表4中可以看出NN-DEC算法，在各个真实数据集上的聚类评价指标结果均优于其他六个对比算法。Iris数据集上分布较散且密度相对分布均匀，NN-DEC算法的聚类性能虽然优于其他几个算法，但是由于密度较均匀其他对比算法聚类性能参数也较好。Cancer数据集维度大、密度分布差异大，NNDEC算法在该数据集上聚类效果较好，KNN-DPC和EC算法在该数据集上聚类性能相当，NNDP算法性能要优于EC和KNN-DPC算法。Wine数据集上密度极值分布明显，数据分布紧凑，所以NN-DEC算法和EC算法聚类性能相差很小，而NNDP算法没有对聚类中心点之间的距离，做自适应处理性能低于EC算法，DBSCAN算法处理密度集中分布的数据集时聚类性能，相较于其他算法更差。Waveform数据集中数据分布集中，局部密度极值容易计算，因此NN-DEC算法的性能优于其他对比算法。Breast数据集上类别数较少，K-means进行划分时聚类效果明显，聚类性能与NN-DEC算法相差不大。Segment数据集上数据分布离散，密度极值分布不均匀，EC算法的聚类性能最差，NNDP和NN-DEC算法局部密度计算效率相当，但对于距离的度量NN-DEC算法更加合理，所以NN-DEC算法聚类效果更优。综上所述NN-DEC算法在UCI真实数据集上的性能是最优的。

表5 各聚类算法在UCI数据集上的评价指标对比Table 5 Comparison of evaluation metrics of various clustering algorithms on the UCI dataset

采用折线图方式来直观表达NN-DEC算法NMI值，整体上优于其他对比算法，如图7。

3.3 算法时间复杂度分析

分别在合成数据集和UCI公共数据集上，对比不同算法在不同数据集下的时间复杂度。

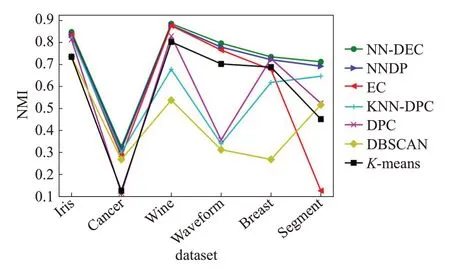
图7 算法在UCI数据集上NMI值Fig.7 Algorithm NMI values on UCI dataset

如图8所示为7种算法在合成数据集Aggregation上运行时间（迭代运行30次取平均值）。

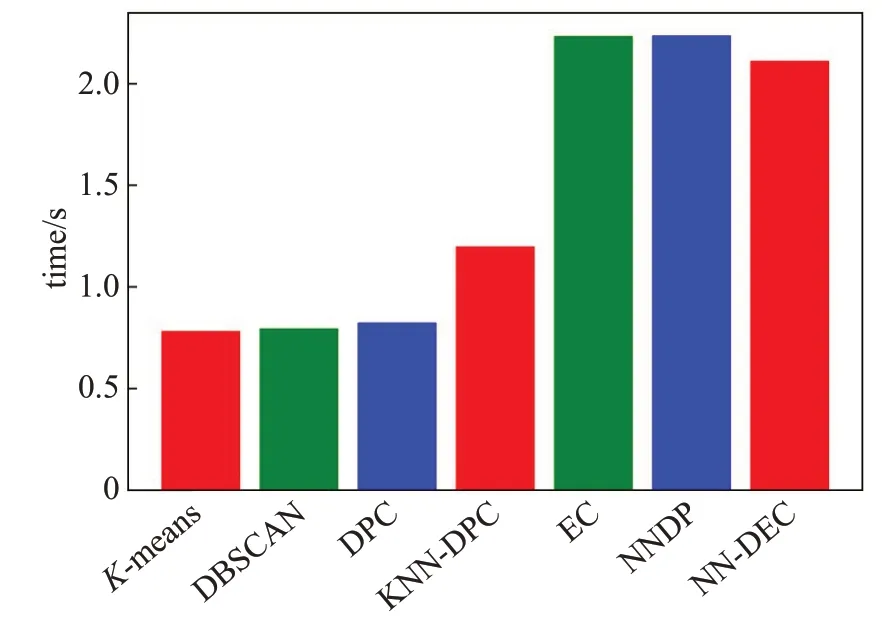
图8 算法在Aggregation数据集上运行时间Fig.8 Algorithm runtime on Aggregation dataset

NN-DEC算法运行时间效率上，比不上K-means和DBSCAN线性时间复杂度的算法，但是在聚类效果上明显优于这两个算法，因为在Aggregation数据集上密度分布差异大，所以本文提出算法时间复杂度优于NNDP和EC算法。

如图9所示为7种算法在UCI数据集Wine上运行时间（迭代运行30次取平均值）。

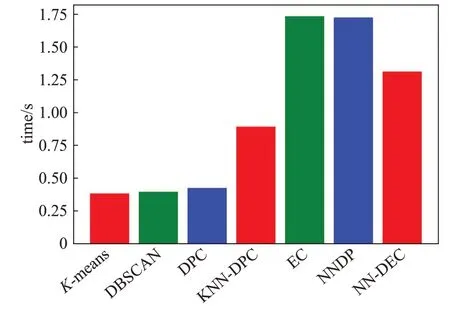
图9 算法在Wine数据集上运行时间Fig.9 Algorithm runtime on Wine dataset

在Wine数据集上密度极值分布明显，离群点容易剔除，所以本文提出算法在时间复杂度上优于NNDP和EC算法。

4 结束语

本文提出了一种自然邻居密度极值算法NN-DEC算法。当数据集密度真实分布差异较大时，采用统一标准去筛选聚类中心，对于低密度区域聚类中心选取存在较大误差，在这个基础上引入连通值概念，采用连通值将数据集进行区域划分，使用数学上极值的概念计算密度极值，以此来找到不同区域的聚类中心点，不同区域分开进行聚类，最后将聚类结果合并到一起。文中对于阈值选取以先前文献的取值为基础，这样会导致对自己算法存在不足，在接下来工作中对于阈值选取可以提出一个模型优化阈值参数选取。每次迭代要更新所有节点连通值消耗时间太久，采用随机游走方式，计算连通值提高算法的效率。可以增加一个空间度量值将数据按层次空间分开，让算法自适应地去处理高维数据集。