交替非负约束框架的海洋传感网协同定位

程 帅，吴华锋，梅骁峻

上海海事大学 商船学院，上海 201306

作为探索海洋的一种重要的工具，海洋传感网（Ocean Sensor Networks，OSNs）在气候预测、资源开发等应用中扮演着关键的角色[1-3]，利用网络中的节点对相应的数据进行采集、处理及分析，能够有效地应对突发的灾难性天气亦或是提高资源开发的效率[4-5]。而在OSNs中，若采集到的数据没有位置信息，则相应的数据将变得没有意义[6-9]，因此定位技术又是OSNs中的一项关键问题[10]。然而，如何在复杂的海洋环境中获取较为准确的位置仍是一个挑战[11-13]。

为此，Huang等提出一种OSNs稀疏性节点定位方法。该方法利用基于到达角度（Angle of Arrival，AOA）的测距方法来估计锚节点与多跳路由节点间的欧式距离[14]。同样地，为解决节点稀疏性导致的定位精度差等问题，Nuo等研究了一种基于水面部署移动锚节点（Surface Deployed Mobile Anchor node，SDMA）的定位方法，利用移动节点在水面上周期性运动来定位目标节点，通过节点的机动性补偿部署稀疏性导致的定位精度低等问题，降低锚节点的部署成本[15]。Zhang等考虑了由于水流引起的OSNs节点运动的问题，提出了基于到达时间（Time of Arrival，TOA）测距策略的OSNs节点定位，利用灰狼优化算法来估计OSNs下一时刻的最佳位置[16]。Zhang等结合移动性预测及粒子群优化算法，进一步提出了一种基于TOA的OSNs定位方法，利用节点的空间相干性对目标节点进行预测，并基于投影定位[17]将三维场景转化为二维场景使用三边定位方法对目标节点定位[18]。Cheng等则利用到达时间差（Time Difference of Arrival，TDOA）的测距方法提出了一种基于最小二乘法（Least Squares，LS）的大规模OSNs目标节点定位法。为进一步提高节点的定位效率，利用已时钟同步的布置在水面的三个锚节点来辅助水下目标节点，通过周期性收发测距信号在三维拓扑中向各个方向进行迭代定位[19]。

相对于TOA、AOA、TDOA等测距技术而言，基于信号强度指示值（Received Signal Strength Indication，RSSI）的测距方法成本较廉价，通信开销较小，不需要TDOA、TOA技术的时钟校正要求，也不要AOA技术天线相控的需求[20]，因此近些年，一些学者开始探索利用RSSI对OSNs中的目标进行定位。Saeed等提出了一种基于RSSI的定位框架，使用基于主优化方法的定位算法（Majorization Approach Based Localization，MABL）来减少每个块内核矩阵的最短路径的定位误差[21]。吕品品通过基于RSSI的球形传播模型来估计目标节点与锚节点间的距离，并结合欧几里德几何学估计目标节点位置[22]。Chang等将定位问题转换为广义信任区域子问题（Generalized Trust Region Sub-problem，GTRS），并进一步研究一种已知发射功率方案和未知发射功率方案的加权最小二乘法（Weighted Least Squares，WLS）[23]。Mei等为减小异常损耗带来的影响，提出了一种稳健的、非协作的定位算法（Robust Non-cooperative Localization Algorithm，RNLA）[11]。该方法在已知先验水深的情况下将三维定位问题转换为二维定位问题。尽管RNLA可以减少异常损耗带来的估计误差，随后进一步提出一种吸收损耗抑制的定位技术[12]，以减少信号吸收损耗带来的额外定位误差。此外，Poursheikhali等提出一种在低传输频率下基于过采样匹配滤波器的RSS定位方法（Oversampled Matched Filter-based RSSI，OSMF-RSSI），以减少水下介质不均匀引起的定位误差[24]。

然而，当网络中存在多个目标时，利用上述定位技术对多目标单一循环依次定位，则相应的定位效率较低。为此，引入协同理论，通过多目标节点间的信息交互，能够有效地提升定位效率，提高定位精度[25]。虽已有相应的协同定位算法在陆地传感网（Terrestrial Wireless Sensor Networks，TWSNs）被提出[25-28]，但不同于陆地的部署环境，高度动态的海洋环境使得网络中所有节点在每一时刻的位置都处于变化，因此直接利用现有的TWSNs协同定位技术，定位精度往往效果不理想。故本文提出一种基于有效集的再优化协同定位（Active Set Method based Re-Estimation Cooperative Localization，ASM-RECL）算法。将原定位问题转化为基于交替非负约束最小二乘（Alternative Nonnegative Constrained Least Squares，ANCLS）的优化问题，利用有效集法（Active Set Method，ASM）通过内外循环寻求优化问题的可行解。然而，在实际解决过程中，基于ASM算法的求解易陷入局部最优，为进一步提升解的质量，改进定位精度，利用一阶泰勒级数线性展开再次构造优化方程，最小化定位误差。此外，为模拟OSNs环境的高度动态性，在实验中节点的位置在每次蒙特卡洛仿真过程中是变化的，并推导得到基于协同定位的克劳美罗下界（Cooperative Localization-based Cramer-Rao Low Bound，CRLB-CL），以此来验证提出算法的有效性。

1 问题描述

假设OSNs水面部署有N个浮标节点以及M个目标节点，第i个锚节点位置表示为ai=[ai1,ai2]T,i=1,2,…,N；第j个目标节点位置为xj=[xj1,xj2]T,j=1,2,…,M，其中T表示转置。网络中节点利用无线电进行通信，节点间通过信息的交互获取RSSI，假设各节点的发射功率相同，利用对数-正态信号损耗模型可相应的RSSI测距值[29]，即：

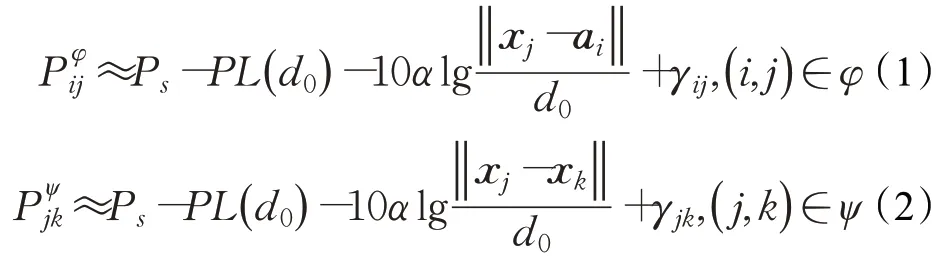
通过最大化概率密度函数，可得到最大似然估计器，即：

但基于最大似然估计，即式（4）具有较高的非凸性，求解相应的全局最优值较为困难，且计算复杂度较高[9]。为此，本文提出一种新的求解思路，将原问题转化至ANCLS框架下，分两步对OSNs的多个目标节点同时进行求解，利用协同理论，避免单一循环地利用相对应的测距值对目标节点依次求解，提高网络的定位效率。

2 基于有效集的再优化协同定位（ASM-RECL）

2.1 ANCLS框架

当γ较小，d0=1 m时，对于第j个目标节点来说，式（1）和式（2）可转化为：

原最大似然估计可转化为最小二乘框架，即：

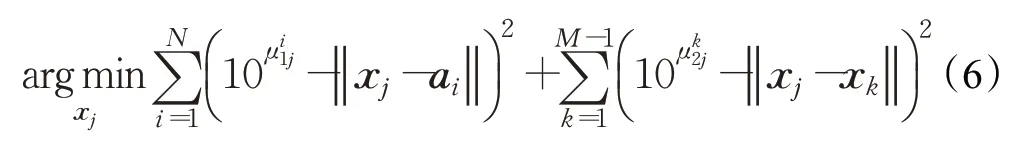
平方式（6）中的每一项并展开后，可得：

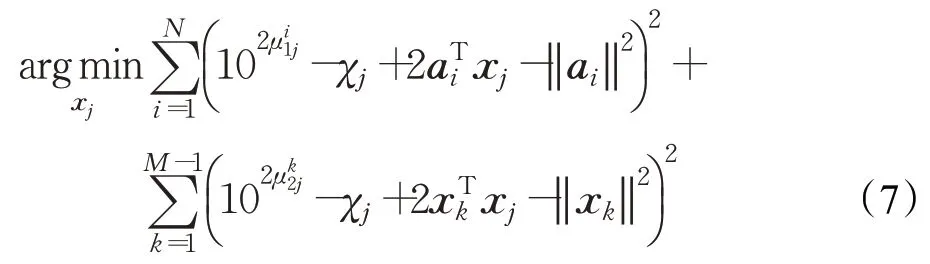
式中：

2.2 有效集法（ASM）

由于ASM能够在有限的迭代次数里获得较高精度的解，相较于其他求解ANCLS框架的问题而言，不仅计算复杂度较低，计算效率亦较好[30]。故本文引入ASM来求解基于RSSI定位的ANCLS问题，即求解式（8）。

假设Γ={1,2,3}表示矩阵ξ的列以及矩阵θ行的索引集合，Λ和Ξ分别为Γ两个子集，代表主动集和被动集，即Λ⋃Ξ=Γ。若存在某一矩阵，并根据将1至3的索引数划分至相应子集Λ和Ξ中，则矩阵的对偶矩阵ϑ͂可表示为。

ASM通过内外循环来将式（8）分解成M个子问题进而求解ANCLS，即：

ASM算法伪代码如下：

具体地：

（1）在外循环过程中利用LS求得可行解，即：

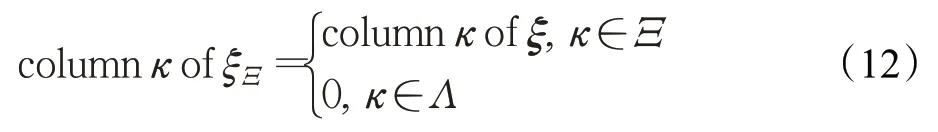
其中κ为被动集Ξ相应索引值。

在求得可行解后，寻找索引l∈Λ使得δl=max{δκ:κ∈Λ}，并将相关索引从主动集Λ移入被动集Ξ中。

（2）在内循环过程，通过约束优化可行解，将约束外的解剔除，即：

通过来回在主动集和被动集间交换可行解索引，进而求得式（8）的解。

2.3 基于一阶泰勒级数展开的再优化

然而，ASM的实质亦是利用LS求解，而LS的求解精度并非全局最优值[29]，为进一步提高解的精度，以ASM求得的解为观测量再构造函数，即：

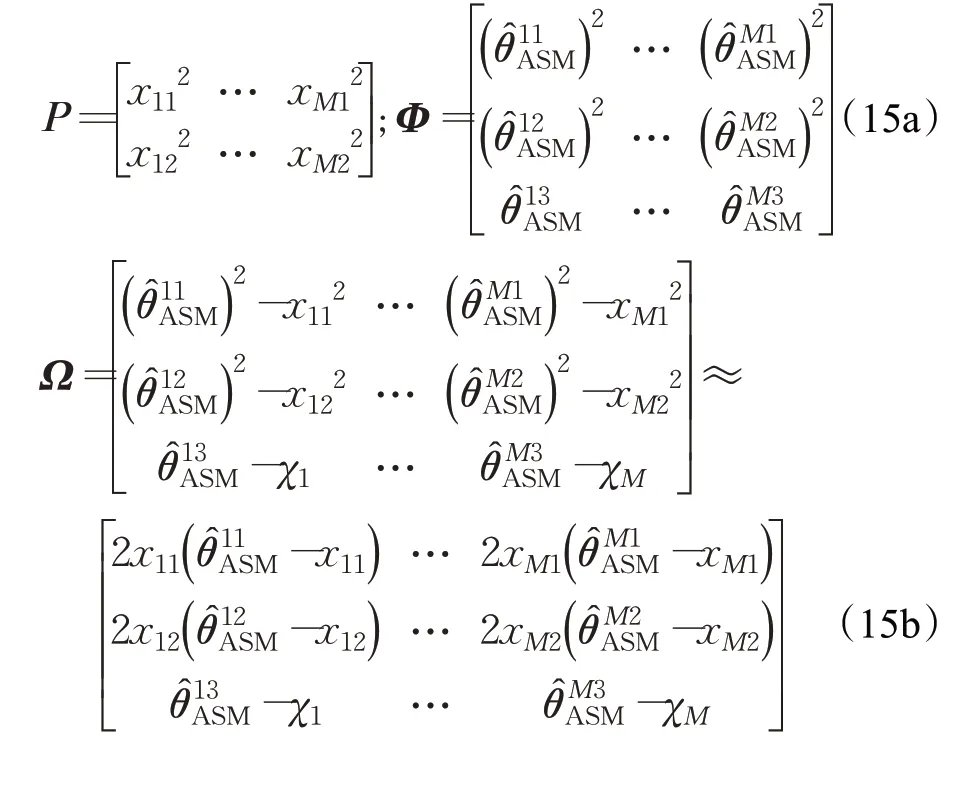
定义ν为关于θ的函数，即：

式（8）则可进一步转化为优化方程：

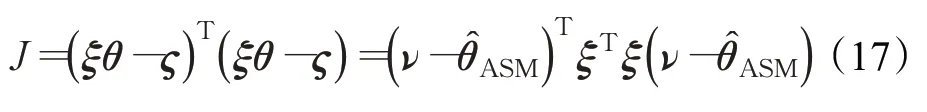
对于第j个目标节点来说，在附近，利用对进行一阶泰勒级数展开，可得：

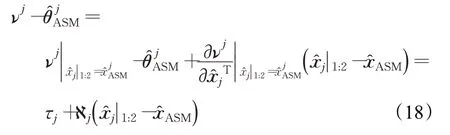
对于M个目标节点来说：

将式（18）代入式（17）可得：

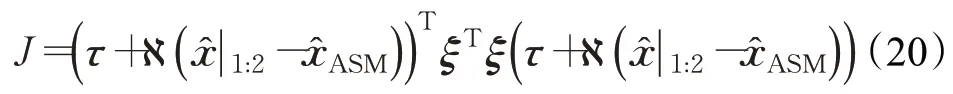
当式（21）的偏导为零时，ASM-RECL可得：

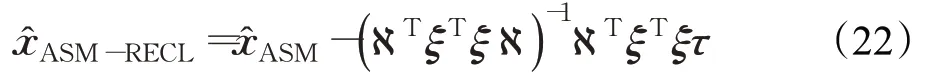
2.4 CRLB-CL

CRLB为无偏估计可能达到的最小方差的理论极限，通常用于评估不同估计算法的性能[31]，它被定义为费雪信息矩阵（Fisher Information Matrix，FIM）逆的迹，即：

式中，tr表示矩阵的迹。

根据式（1）和式（2），对于第j个目标节点来说：

对于M个目标节点来说，设，则：

对于Fx来说，每一列表示第j个目标节点相较于锚节点的观测值以及其他未知节点k的观测值对于的一阶导，其中0表示k=j；第1行至第N行的值表示第i个锚节点相较于未知节点的观测值对于的一阶导，第N+1行至N+M行的值表示第j个目标节点相较于其他未知节点k的观测值对于的一阶导，其中0表示k=j。而Fy与Fx同理，但是相对于的一阶导。

相对应的FIM可表示为：

式中，n表示蒙特卡洛仿真次数，MC表示蒙特卡洛仿真总次数。

3 仿真结果分析

为验证提出算法的有效性，仿真实验在Matlab R2018b进行，仿真区域35 m×35 m，P0=-55 dBm，α=3.5，MC=1 000。此外，由于海洋环境的动态性，在每一次的蒙特卡洛仿真过程中，网络中的节点位置在区域中动态变化，服从随机游走模型[33]，通过在不同条件下对比基于ASM的非协同定位（ASM-based Non-Cooperative Localization，ASM-NCL）[9]、基于LS的协同定位（LS-based Cooperative Localization，LS-CL）[29]、基于LS的非协同定位（LS-based Non-Cooperative Localization，LS-NCL）[24]，以及基于协同思想推导得到的ASM-CL，基于本文算法ASM-RE推导得到的非协同ASM-RENCL、CRLB-NCL以及推导得到的协同CRLBCL，利用NRMSE作为基准评判算法的有效性，即：

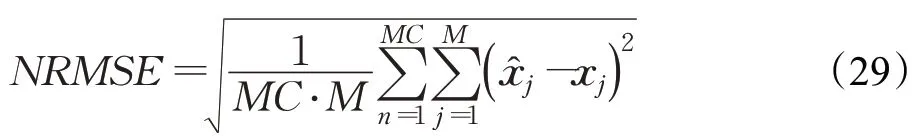
3.1 不同锚节点数量下的定位误差

为探究不同锚节点数量情况下的定位误差，仿真设置M=3，σi=5 dB。在该条件下相应的误差如图1所示。由于锚节点数量的增多意味着网络中可用的测距信息相应增加，故各算法的定位误差随着锚节点数量的增多而减小。与非协同定位相比，协同定位除了锚节点的测距信息外，还包含有其他目标节点的测距信息，故各算法的协同定位的定位误差比非协同定位要来得小。其中，ASM算法的实质虽然是利用LS解决，但增加了相应的约束条件，在第二阶段的内循环过程中剔除了约束条件外的可行解，因此定位精度相比于LS要来得高。而ASM-RE在ASM算法的基础上，通过一阶泰勒级数进行误差最小化的线性展开，再构造优化方程，进一步改善了定位精度。因此从图1中可以看出，无论是协同定位ASM-RECL亦或是非协同定位ASM-RENCL，其定位精度都比其他算法来得高，并且更接近CRLB。

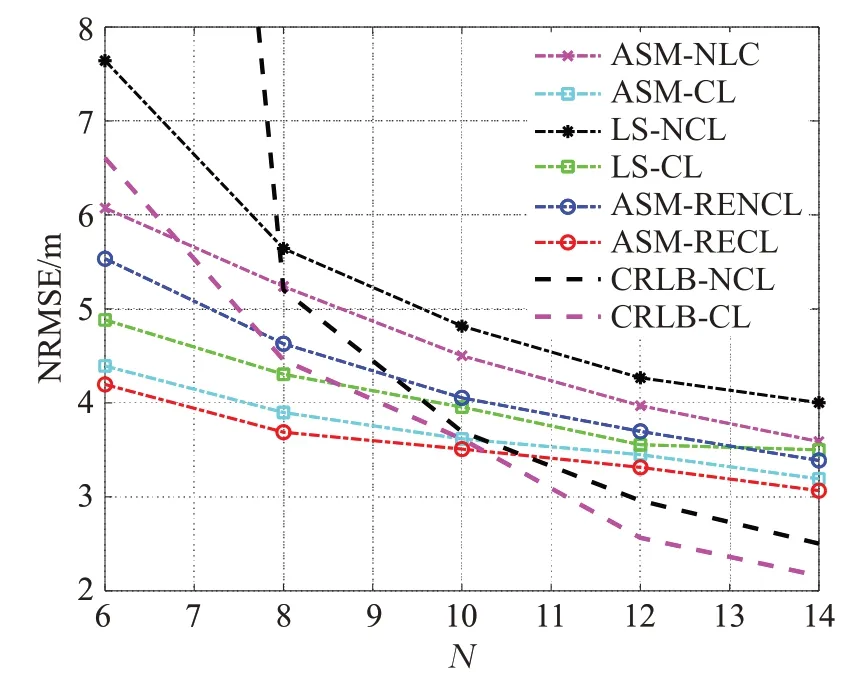
图1 不同锚节点数量情况下的定位误差Fig.1 Localization error under different number of anchors

3.2 不同噪声条件下的定位误差

为探究不同噪声条件下的定位误差，仿真设置M=3，N=10。在该条件下相应的误差如图2所示。如预期一样，噪声的增加导致定位误差的增大。从图2可以看出，各算法随着噪声的增大相应的定位精度也变得越差，其中基于协同定位的算法相比于基于非协同定位算法的误差小。当噪声较小时，各算法的定位精度较为接近，而当噪声逐渐增大时，相对应的算法精度的差别显现则较为明显。对于采用了一阶线性展开的ASM-RE来说，其非协同定位的精度甚至好于基于协同定位的LS-CL。而相应的协同定位ASM-RECL的精度相较于其他的方法来说误差较小，且更接近于CRLB-CL。

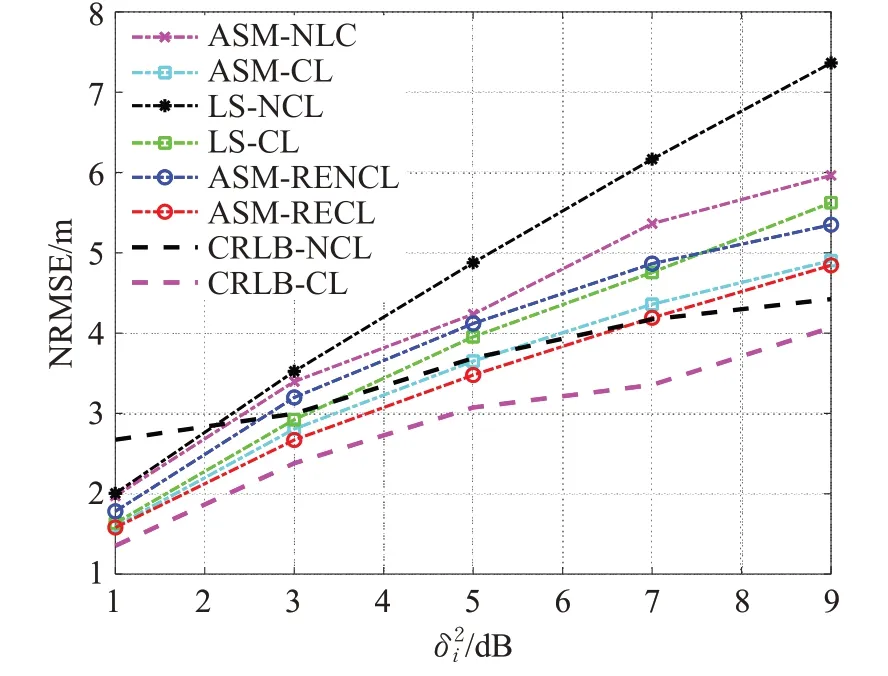
图2 不同噪声条件下的定位误差Fig.2 Localization error under different variances

3.3 不同目标节点数量的定位误差

为探究不同目标节点数量对定位误差的影响，仿真设置N=10，=5 dB。各算法在不同数量目标节点下的定位误差如图3所示。从图中可以看出，利用锚节点与目标节点及目标节点间的协同进行定位的精度要显著好于只利用锚节点与目标节点的非协同定位。当目标节点较少时，目标节点间可交换的测距信息较少，因此相应的非协同定位精度与协同定位精度差别较小。而当目标节点数量增多时，相应的目标节点收到的测距信息亦增多，故协同定位与非协同定位的定位精度会有所差别。此外，由于目标节点数量的增多，虽然交互的测距信息增多有益于定位精度相比于非协同定位有所改进，但是已知位置的锚节点是一定的，因此随着目标节点数量的增多，总体的定位误差是有所下降的。在其中，ASM-RECL的定位精度比其他算法来说更为优越。

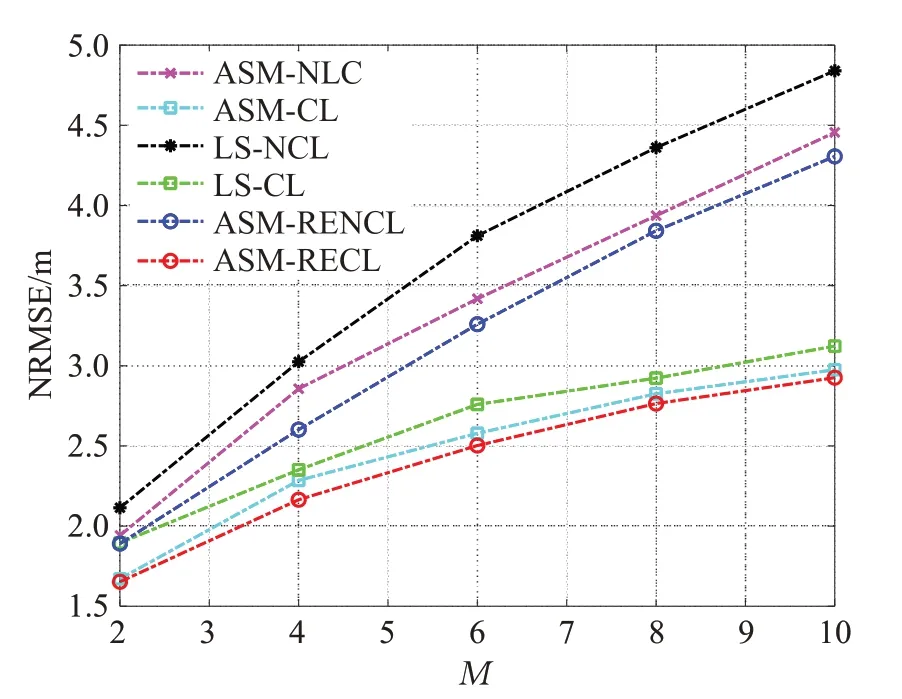
图3 不同目标节点数量的定位误差Fig.3 Localization error under different number of targets

3.4 累计密度函数（Cumulated Distributed Function，CDF）

为进一步探究本文提出算法在协同定位方面的优越性，基于上述三个仿真实验的在每个场景下的仿真条件，对相应的CDF进行仿真，结果如图4所示。在不同锚节点数量条件下的CDF，如图4（a）所示，从图中可以看出，对于ASM-RECL而言，其接近100%，而ASM-CL和LS-CL来说，在达到相同概率时分别为和；在不同噪声条件下的CDF，如图4（b）所示，从图中可以看出，对于ASM-RECL而言，其接近100%，而ASM-CL和LS-CL来说，在达到相同概率时分别为和；在不同目标节点数量条件下的CDF，如图4（c）所示，从图中可以看出，对于ASM-RECL而言，其接近100%，而ASM-CL和LS-CL来说，在达到相同概率时分别为和。

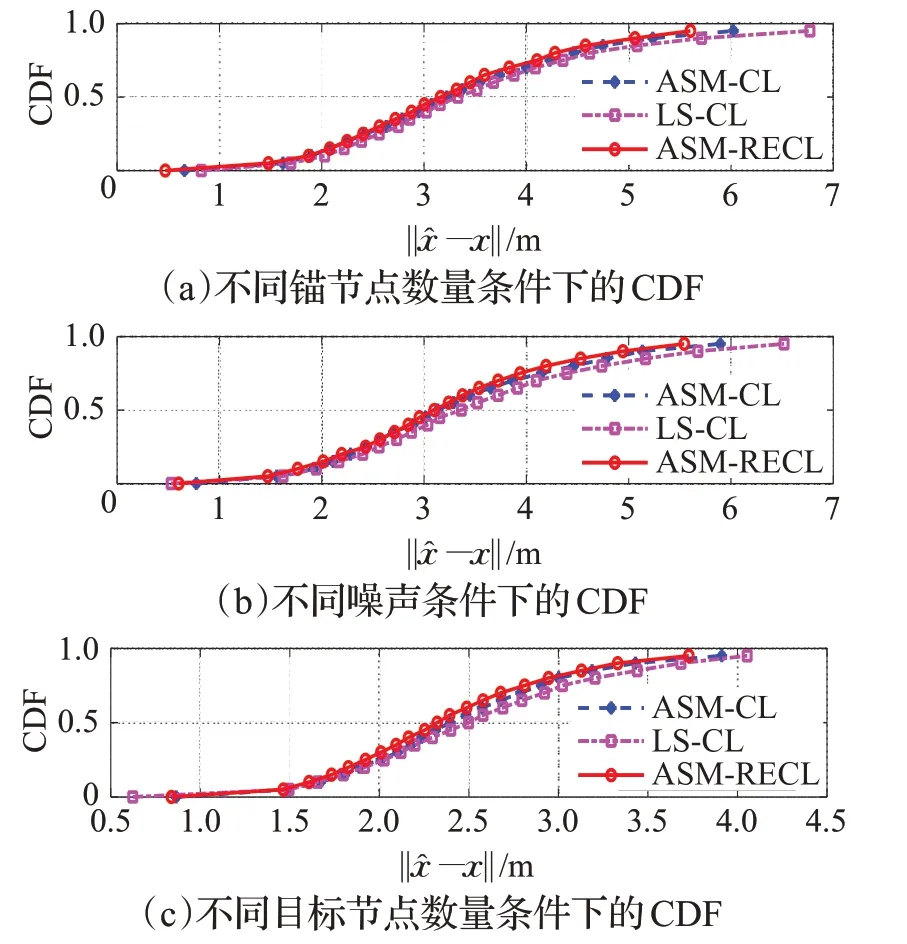
图4 不同条件下对应的CDFFig.4 Corresponding CDF under different conditions

3.5 各定位方法在相对静态TWSNs的定位误差

不同于相对高动态性的OSNs，TWSNs节点通常是静态部署。为探究本文提出方法是否能够在相对静态的TWSNs网络中也有着在OSNs的良好定位表现，仿真在不同噪声条件下进行，且设置N=10，M=3。静态的部署场景如图5所示。

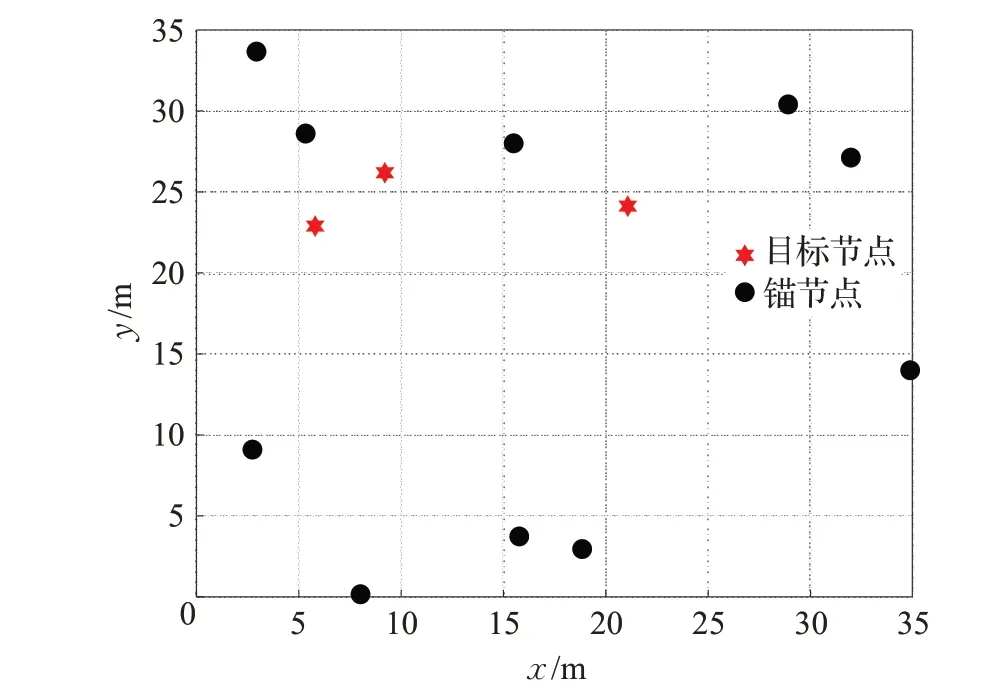
图5 TWSNs节点静态部署场景Fig.5 Static deployment scheme of nodes for TWSNs

从图6的定位误差可以看出，在TWSNs中，不同噪声情况下各个方法的定位效果较为接近，且都随着噪声的增大而变差。本文提出的算法虽然在某些条件下的定位效果稍逊于现有算法，但总的来说其在相对静态的TWSNs中仍具有较好表现。相比之下，在动态性较高的OSNs，即每一时刻节点位置处于变化的状态，本文提出的算法具有较好的鲁棒性，且从图1到图4的结果中可以看出，其定位效果的优越性相较于静态的TWSNs来得明显。因此，在某种程度上，本文提出的算法更适用于动态性较高的OSNs，能够为OSNs提供较为准确的目标节点位置信息。

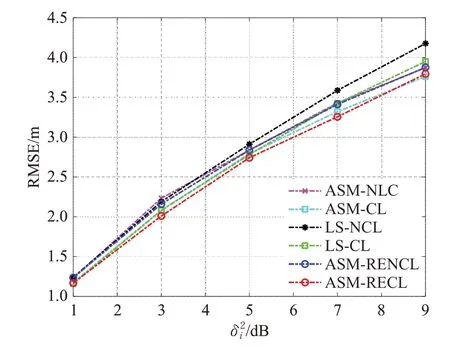
图6 在静态部署中不同噪声条件下的定位误差Fig.6 Localization error under different variances in TWSNs

4 结语

本文提出一种OSNs协同定位算法，即ASM-RECL。将原非线性非凸的定位问题转化在ANCLS框架下，利用ASM内外循环进行解决。为进一步提升解的质量，一阶泰勒级数进行误差最小化的线性展开，再构造优化方程进行求解，以提高定位精度，并推导得到了基于协同定位的CRLB对提出算法进行审查，以评估算法的有效性。此外，为模拟海洋高度动态的环境，网络中所有的节点在每一次蒙特卡洛仿真中的位置不固定，并遵循随机游走模型。实验结果表明，提出的协同定位算法能够有效地提高定位精度，并且无需单一循环依次对目标进行定位，利用相关节点间的测距信息求解多目标节点位置，有效地提高了定位的效率。由于海洋传感网节点能量有限，因此如何简化定位过程的计算复杂度，获取轻量级的定位算法是未来需要进一步研究的内容。