异构集成代理辅助多目标粒子群优化算法

陈万芬，王宇嘉，林炜星

上海工程技术大学 电子电气工程学院，上海 201620

近年来，进化算法由于其解决复杂多目标优化问题的优势被广泛应用于科学和工程的各个领域。但是为了达到所需的收敛效果，进化算法需要进行大量的适应度评估。例如，在汽车工业中进行一次防撞分析需要36～160个小时，若要求解两变量工程问题，至少需要50次迭代，每次迭代至少需要一次仿真模拟，那么整个求解设计过程至少要耗费2个月的时间[1]，在实际工程优化问题中显然是难以接受的。为了缓解上述问题，通常使用计算廉价的代理模型代替昂贵的实际适应度评估。

代理模型是指近似的数学模型，它可以代替更复杂、更耗时的数值分析。在样本数据集上构建代理模型以逼近候选解的适应度值的计算，这类方法称为代理辅助进化算法（Surrogate-Assisted Evolutionary Algorithm，SAEA）。许多分类或回归技术都可以用作代理模型，如径向基函数网络（Radial Basis Functions Network，RBFN）[2]、响应面方法（Response Surface Methodology，RSM）[3]、Kriging[4]和支持向量回归（Support Vector Regression，SVR）[5]。不同的代理模型可以针对性地解决不同问题[6]，如RBFN模型用于高阶非线性问题，Kriging模型用于高维空间中的低阶非线性问题。然而对于大多数实际问题，其特征是未知的，难以通过单一代理模型解决，通常使用代理集成来提高模型的近似性和预测的准确性[7-8]。

集成模型通过使用多个代理模型来减少计算时间，通常有两种集成模型方法。一种是Singh等人[9]提出的选择一个在不同代理模型中具有最高准确性的代理模型来评估个体。另一种是Lim和Jin[10]提出的使用不同的代理模型评估具有不同权重系数的个体，将代理模型的集成与提出的广义代理多目标模因算法结合使用。Singh等人[9]提出了代理模型辅助模拟退火算法，使用集成的代理模型与受约束的Pareto模拟退火作为进化算法框架，根据均方根误差选择代理模型对个体进行评估。Martinez和Coello[11]提出了使用代理模型辅助分解的多目标进化算法，将径向基函数用作集成模型，算法中为每个目标函数建立了代理模型。还有一些研究使用多个代理模型作为集成来近似函数，实验结果表明，在集成机器学习模型中，集成基础学习者输出的预测方差可用于近似适应性预测中的不确定性程度[6]。尽管在集成代理方面研究者已经作了大量的工作[6，11-12]，但是大多数都使用集成来提高适应度近似的准确性，很少关注集成的不确定性信息[13]。因此，研究集成的不确定性信息，对提高代理模型的预测能力具有重要意义。

为了使集成代理辅助进化算法获得满意的优化结果，需要不断提高集成代理模型的预测精度，通常是选择新的样本点并将其添加到样本集中来更新代理模型以提高拟合精度。但是，添加点的过程需要大量的采样点，例如广义回归神经网络（Generalized Regression Neural Network，GRNN）和RBF集 成 的SAEA需 要3 000个采样点[14]。对创伤系统设计问题的单个函数评估需要处理40 000个紧急事件记录样本点[15]。但是，在许多实际的优化问题中，训练集中的数据通常很少。在机翼减阻优化设计中，仅给出了70组数据作为初始采样点[16]。当采用添加点的方法来解决这些问题时，预测精度急剧下降，因此不适用解决样本数据少的问题。

如上所述，大多数现有的SAEA是基于大数据样本集的，关于基于小样本数据集对SAEA的研究相对较少。对于小样本数据集，不仅可用数据量很小，而且在数值噪声和高维优化方面仍然存在问题[17-18]。因此，如何最大程度地利用样本数据来构建高质量的代理模型成为急需解决的问题。本文提出了异构集成代理辅助多目标粒子群优化算法，当训练集中的数据较小时，将训练集划分为几个子集，然后在每个子集上训练代理模型，最后将它们组合成高精度的代理集成。同时，为了在收敛质量和效率之间取得平衡，将全局优化与局部优化相结合。使用Kriging和RBFN建立代理模型，前者用于全局优化，后者用于局部优化，这将在一定程度上缓解高维优化的耗时问题。

1 多目标粒子群优化算法和代理模型

1.1 多目标优化问题

通常情况下，多目标优化问题（Multi-objective Optimization Problems，MOP）包含多个相互冲突的目标，以最小化目标为例，一般MOP可以描述如下：

其中，x=(x1,x2,…,xn)T∈Ω为n维决策变量（向量），为决策空间，由m个相互矛盾的目标函数组成，ℝm为目标空间，fi(x)表示第i个目标函数。

若决策变量x(1)∈Ω和x(2)∈Ω满足：

则称决策变量x(1)支配决策变量x(2)，记为x(1)≺x(2)。在MOP中，当一个解不受任何其他解支配时，则可以称为Pareto最优解。在搜索空间中，所有Pareto最优解的集合形成的权衡曲面，称为Pareto前沿。

1.2 粒子群算法

粒子群（Particle Swarm Optimization，PSO）算法是一种基于鸟群的随机搜索算法[19]。PSO算法利用个体最优和全局最优引导整个群体的寻优，其位置和速度更新公式如下：

由于粒子群算法具有设置参数少、运行效率高、易于实现等优点，近年来在群智能优化领域中被广泛使用。但是粒子群算法存在易陷入局部最优和算法后期收敛速度慢等问题，所以出现了很多改进的粒子群算法。如为了提高算法的搜索能力，采用反向学习策略来增强算法的全局搜索能力[20-21]；通过构造动态子空间并随机对其单维进行变异增强粒子精细搜索的能力[22]。

1.3 代理模型

（1）Kriging模型。Kriging是在高斯过程（Gaussian Process，GP）理论基础上进行建模的有效插值方法[4]，该方法不仅能预测未知点的函数值，还可以提供预测不确定性的程度，提高模型的搜索能力。Kriging模型不仅能找到最佳的线性无偏估计值，同时还能使预测的均方误差最小。Kriging模型由用于全局趋势预测的多项式项和用于局部偏差回归的高斯过程项组成，可以表示为：

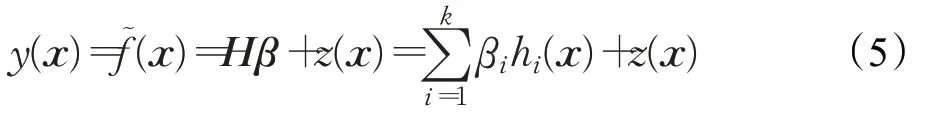
其中，x={x1,x2,…,xn}为n维设计空间的设计矢量，y(x)为预测函数值，线性回归反映了原始函数的整体趋势，hi(x)为回归模型的基函数，β={β1,β2,…,βk}代表相应的回归系数向量，k是基函数hi(x)的数量，高斯过程z(x)服从均值为0，方差为σ2的正态分布。

（2）RBFN模型。RBFN是常用的代理模型之一，可以用作代理模型的局部搜索[2]。RBFN是具有单个隐藏层的前馈神经网络，其结构由输入层、隐含层和输出层组成。隐藏层节点的激活函数为径向基函数，包括高斯函数、反射Sigmoid函数和逆多二次函数，径向基函数的基本形式为：

其中，xi={xi1,xi2,…,xin}表示第i个训练样本，n和N分别是变量数和训练样本数，α={α1,α2,…,αN}表示权重系数，‖·‖为欧几里德范数即待测点x与数据中心ci之间的欧氏距离，φ(·)为核函数即径向函数，内核的典型选择包括线性样条、三次样条、多二次方、薄板样条和高斯函数[23]。

2 异构集成代理辅助多目标粒子群优化算法

2.1 算法框架

代理模型广泛应用于群智能计算中，许多不同适应度形态特性的优化问题的实验结果表明，RBFN在训练数据小的情况下，各类非线性度不同的问题表现最好[24]。并且随着搜索维度及规模的增加，RBFN也能有较好的表现。Kriging作为一类统计学习模型，非常适合于捕捉复杂优化问题的全局场景，并能获得与RBFN相媲美的结果。

为了能够快速有效地解决不同形态的优化问题，本文提出了异构集成代理辅助多目标粒子群优化算法，其结合了Kriging与RBFN的优点，构建能解决不同形态问题的异构集成模型，并采用多目标粒子群优化算法作为搜索算法，提高种群对未知解的搜索能力。本文所提算法框架如图1所示。

图1 异构集成代理辅助多目标粒子群优化算法框架图Fig.1 Framework diagram of heterogeneous ensemble surrogate-assisted multi-objective particle swarm optimization algorithm

从数据库中选取需要的样本形成样本子集，根据采样得到的样本子集构建所需的代理模型，分别为Kriging模型和RBFN模型，再将其通过平均加权法进行异构集成。对建立的异构集成模型进行误差分析，若不满足要求，则需要增加样本点，然后利用整个设计空间中的样本点更新代理模型。最后利用多目标粒子群优化算法对异构集成模型进行优化，得出目标函数最优解集，这在一定程度上减少了多目标粒子群算法的评价次数，降低了计算成本。

异构集成代理辅助多目标粒子群优化算法具体步骤如下：

步骤1使用最优拉丁超立方设计[25]（Optimal Latin Hypercube Design，OLHD）方法从设计空间中选取初始样本点，并将这些设计样本点保存到样本点数据库中，所选的样本点个数为11D-1，其中D为决策变量个数，计算样本点所对应的目标函数值并保存到目标函数样本数据库。

步骤2由决策变量样本点和目标函数样本数据集构造各个优化目标关于决策变量的异构集成模型。

步骤3对构造的异构集成模型进行误差分析，若不满足要求，则需要再次使用OLHD方法来增加样本点，重新建立异构集成模型；若满足要求，则进入下一步。

步骤4初始化种群中各个粒子的位置和速度，并设置群体大小、惯性权重、加速度系数和迭代次数等参数值。

步骤5采用步骤1～步骤3构造的异构集成近似模型计算各个粒子的适应度值，并把非支配解存储到外部存档中。

步骤6根据式（3）和式（4）更新各个粒子的位置和速度，重新计算各个粒子的适应度值，进而更新它们的个体极值、全局极值以及外部存档。

步骤7以所得粒子是否接近全局最优解作为收敛条件，若未达到收敛，对种群进行更新，并返回步骤5；若收敛，则得出Pareto最优解集。

在算法运行过程中，构造Kriging模型和RBFN模型的计算复杂度都是O(n3)，n是训练样本的大小，所以集成模型的计算复杂度为O(n3)。多目标粒子群优化算法的计算复杂度为O(N×D)，其中N为初始化种群的大小，D为决策变量个数。因此所提算法的整体计算复杂度为O(n3)+O(N×D)。

2.2 构建异构集成代理模型

在机器学习策略中，集成学习通过灵活地组合多个学习器来获得更好的泛化能力[26]，集成学习一般结构是先产生一组同种类型或不同类型的个体学习器，再用某种策略将它们结合起来，其结构如图2所示。理论上已经证明，当多样性和准确性之间达到适当的平衡时，集成模型可以提供比单个模型更准确的预测[27]。

图2 集成学习示意图Fig.2 Schematic diagram of ensemble learning

本文使用加权平均法作为集成代理模型的结合策略。加权平均法是集成学习中计算简单、可行性较高且易于理解的模型融合方法，该方法将多个模型按照一定规则加权平均后输出融合结果[6]，具体如下：

式中，ei是第i个代理模型的均方根误差。由公式（9）可以看出，预测误差较小的代理模型被分配的权重较大。在本算法中，用均方根误差作为误差的测量方法，每个代理模型的均方根误差如下：

式中，m是样本数目，e(xi)是点xi的预测误差。

本文选用两种不同类型的学习算法作为集成模型的个体学习器，称为异构集成模型，即通过两种不同的建模方法形成两种代理模型，然后通过加权平均法将两种代理模型组合成为一个高精度、鲁棒性强的异构集成代理模型。异构集成代理模型只需要一个搜索种群，因此所需的数据量较少，适用于数据量少的情况。在许多代理模型中，Kriging模型具有很好的非线性函数近似性，并且在中低维度上具有良好的性能。RBFN模型在建模过程中遍历所有训练数据，因此非常适合探索局部适应度场景并在高维问题上表现出色。因此，本文选择Kriging和RBFN来构建代理模型并通过加权平均法将两者结合形成异构集成代理模型，其中Kriging模型用于全局优化，RBFN模型用于局部优化，以获取收敛性并能缓解高维优化的耗时问题。异构集成代理模型的形成方法如图3所示。

图3 异构集成代理模型的形成方式Fig.3 Formation of heterogeneous ensemble surrogate model

在图3中，集成代理模型通过一个种群中的数据产生了两个不同的代理模型，分别是Kriging模型和RBFN模型，将两个代理模型通过加权平均法相集成。加权平均法本身不需要其他背景理论知识，可以直接使用，简单方便，但是在模型集成过程中会依赖其成员的权重，所以有一些不依赖于权重的改进方法[26]，例如投票法（Voting）、堆叠法（Stacking），虽然它们不需要权重来进行模型融合，但其计算复杂度较高，特别是Stacking方法需要进行多轮模型融合，这将会使训练时间加长。

异构集成代理模型的构造方法如下：

（1）对种群用精确适应度函数求出其适应度值。

（2）根据种群位置及适应度值构建Kriging模型与RBFN模型。

（3）求出两个代理模型的均方误差，根据加权平均法更新各个代理模型的权重。

（4）将Kriging模型与RBFN模型按各自的权重组合成异构集成代理模型。

异构集成代理辅助多目标粒子群优化算法的基本步骤如下：

步骤1初始化。初始化阶段包括种群的初始化与两个代理模型的初始化。种群的初始化是基于样本数据库，样本数据库中的数据是通过在待优化区域用OLHD方法随机采样产生。对种群初始化时，随机选取数据库中11D-1个样本点构成初始化的种群。根据种群中粒子的信息，用Kriging模型及RBFN模型构建初始化的两个代理模型。

步骤2异构集成代理模型的构建。根据加权平均法求出两个代理模型各自的权重，并根据权重将两个代理模型组成为异构集成代理模型。

步骤3种群的更新。根据多目标粒子群优化算法更新种群中各个粒子的位置与速度。

步骤4代理模型更新。在不满足代理模型精度要求时，需要更新异构集成代理模型，其更新方法参见以上异构集成代理模型的构造策略，在满足代理模型精度要求时，利用异构集成代理模型对新更新的候选解作评价，并选出预测结果最好的粒子对其用精确适应度函数评价。

步骤5终止条件的判断。若满足终止条件，停止算法，否则，转至步骤3。

3 实验分析

本文将使用5个具有不同复杂程度的常用数值函数ZDT1～ZDT4和ZDT6来测试所提算法的适用性和效率[28]。测试实例ZDT1的决策变量为4个，ZDT2～ZDT4和ZDT6的决策变量为10个，而目标函数数量为2个。使用非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm II，NSGAII）[29]和基于拥挤距离和epsilon占优的多目标粒子群优化算法（Optimal Multi-Objective Particle Swarm Optimization algorithm，OMOPSO）[30]分别与异构集成代理模型结合并进行比较，分别称为HE-NSGAII和HE-OMOPSO；使用NSGAII和OMOPSO分别与单个代理模型Kriging结合并进行比较，分别称为K-NSGAII[31]和K-OMOPSO[32]；将异构集成代理模型与单个代理模型进行比较。此外还将新提出的HEOMOPSO与OMOPSO和NSGAII进行了比较，从而证明使用异构集成代理模型在优化昂贵问题中的重要性。计算了解决这些基准函数时的覆盖率度量，并将其与未使用代理模型的OMOPSO和NSGAII的覆盖率度量进行比较，为了减少随机误差的影响，每个测试函数都进行了10次实验。

3.1 基准测试

实验选用了ZDT系列测试函数，分别是ZDT1、ZDT2、ZDT3、ZDT4和ZDT6。由于ZDT5是一个二进制问题，对于Kriging模型来说很难估计，所以不适合所提出的方法。基准测试问题具有多种特征，例如凸、非凸、不连续和多边问题。ZDT1是具有简单边界的凸函数，ZDT2～ZDT4和ZDT6是高维测试问题，其中ZDT2是连续的非凸函数，ZDT3是由非连续的Pareto前沿组成，ZDT4是高度多模态函数，包含了219个局部极值，而ZDT6位于Pareto前沿的解密度较低，并且其Pareto最优解分布不均匀，Pareto前沿是非凸的。这些基准测试函数具有不同程度的复杂性，因此可以有效地说明所提出的HE-OMOPSO算法的适用性。

3.2 性能指标

本文选择世代距离指标（Generational Distance，GD）[33]、间距指标（Spacing，SP）[34]和超体积指标（Hyper-Volume，HV）[35]分别评价算法的性能。

GD指标由Pareto最优解集中的每个点到参考集中的平均最小距离表示，GD值越小，说明算法的收敛性越好，也表明了近似Pareto前沿解集有较好的收敛性。GD指标的计算公式如下：

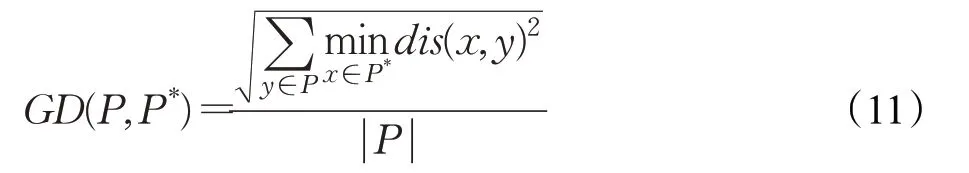
其中，P是由算法获得的近似Pareto解集，P*是从目标空间真实Pareto前沿上采样的一组均匀分布的参考集，是到目前为止找到的非支配解的数量，而dis(x,y)表示解集P中的点y和参考集P*中的点x之间的欧氏距离。

SP指标可以用来测量解集分布的均匀性，该指标通过计算解集中每个解到其他解的最小距离的标准差获得，SP值越小，说明解集越均匀，算法的多样性越好，也表明了近似Pareto前沿解集有较好的多样性。SP指标的计算公式如下：

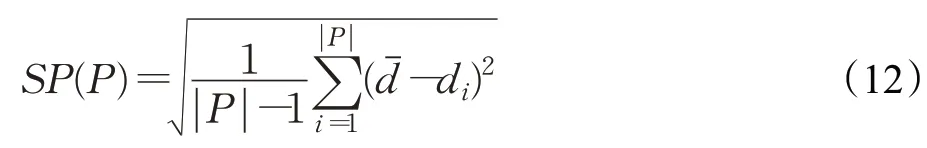
其中，di表示第i个解到解集P中其他解的最小距离，dˉ表示所有di的均值。

HV指标可以捕获一组非支配解的收敛性和多样性，因此本文将其用作评价多目标优化算法的综合性能。该性能指标用于度量一个目标空间的体积，即算法获得的非支配解集与参考点围成的目标空间中区域的体积，HV指标值越大，说明算法的综合性能越好，也表明了近似Pareto前沿解集有较好的收敛性和多样性。HV指标的计算公式如下：

其中，δ表示Lebesgue测度，用来测量体积，||S表示非支配解集的数目，vi表示参考点与解集中第i解构成的超体积。在本文中，所有比较算法均用于指定HV的参考点得出了非支配解的最大和最小目标值，即最小参考点和最大参考点分别为[0，0]和[11，11]，HV值均归一化为[0，1]。

3.3 实验结果与分析

假设目标函数的计算在实验过程中是昂贵的，M、D分别代表所有测试实例中的目标数、决策变量数（维度数），算法参数设置如表1所示，对于所有比较算法，独立运行次数为10次，在每次运行中，初始训练数据都是新生成的。

表1 算法参数设置Table 1 Algorithm parameter settings

为了比较常规的NSGAII、OMOPSO、K-NSGAII、K-OMOPSO和HE-NSGAII与新提议的HE-OMOPSO，所有实验均使用相同的初始种群。在10次实验中，记录了每种算法的实际仿真成本数量以及通过这些方法获得的非支配点。然后，针对每次实验计算GD、SP和HV三个性能指标，实验仿真结果如图4～图8所示。

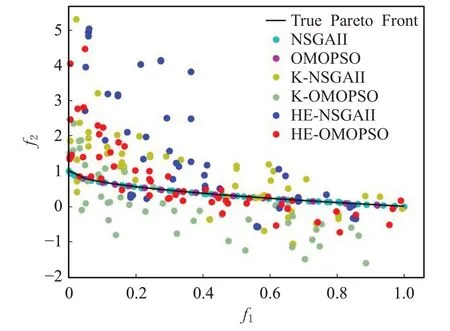
图4 测试函数ZDT1的Pareto前沿Fig.4 Pareto front of test function ZDT1

图5 测试函数ZDT2的Pareto前沿Fig.5 Pareto front of test function ZDT2

图6 测试函数ZDT3的Pareto前沿Fig.6 Pareto front of test function ZDT3

图7 测试函数ZDT4的Pareto前沿Fig.7 Pareto front of test function ZDT4

测试结果表明，与OMOPSO、NSGAII、K-NSGAII、K-OMOPSO和HE-NSGAII相比，新提出的方法在ZDT1、ZDT2、ZDT3和ZDT6测试函数上表现较好，除ZDT4外。从图4～图6中可以看出，新提出的方法在真实的Pareto前沿上的分布性和均匀性比K-NSGAII、K-OMOPSO和HE-NSGAII的效果更好，在收敛性上与OMOPSO和NSGAII相比，效果较差，但是该方法使用了较少的适应度函数评估次数获得了更好的近似值。从图7中可以看出，新提出的方法与HE-NSGAII相比，收敛性较差，与K-NSGAII和K-OMOPSO相比，收敛效果较好，这是由于ZDT4函数的复杂性使得单个代理模型更难于近似真实函数，这体现出了异构集成代理模型的优势，而与OMOPSO和NSGAII相比，生成的近似值更接近真实的Pareto前沿。从图8中可以看出，新提出的方法在收敛性和分布性上比其他算法表现都好，除了生成更接近真实的Pareto前沿的点外，还生成沿其更好分布的点。

图8 测试函数ZDT6的Pareto前沿Fig.8 Pareto front of test function ZDT6

以测试函数ZDT1为例，分别从GD、SP和HV三个性能指标说明算法的有效性。从图9和图10中可以看出，随着迭代次数的增加，本文所提方法能较快地收敛，并且解集分布也较均匀，算法在收敛性和多样性方面取得较好效果，这是因为所提方法使用异构集成模型，加快了收敛速度，而在异构集成模型中加入RBFN模型用于局部搜索优化，提高了算法的多样性。从图11中可以看出，随着迭代次数的增加，HE-OMOPSO的HV值虽然多次陷入局部最优，但是能够很快地跳出，然后继续迭代到HV值收敛，这是因为加入了RBFN模型用于局部搜索优化，而Kriging模型用于全局搜索优化，两者相结合，加快了收敛速度。从图12中可以看出，随着评估次数的增加，HE-OMOPSO能较快地收敛，在达到相同的收敛指标时，OMOPSO的评估次数是本文所提算法的10倍。

图9 GD值收敛性比较Fig.9 Comparison of GD value convergence

图10 SP值多样性比较Fig.10 Comparison of SP value diversity

图11 综合指标HV值比较Fig.11 Comparison of comprehensive metric HV value

图12 算法评估次数比较Fig.12 Comparison of algorithm evaluation times

由于ZDT2和ZDT6的Pareto前沿的特殊性，可以用来测试算法的收敛性能。从表2和表3中可以看出，本文所提方法在ZDT2、ZDT6中取得了最小的GD值，这说明使用异构集成模型可以提高算法的收敛性。因为异构集成中的Kriging模型可以使预测误差减小，从而使算法的全局搜索能力增强。而在分布性方面，HEOMOPSO在ZDT6中的SP值接近于0，与其他算法相比，多样性较好，这说明使用异构集成模型可以提高算法的多样性，异构集成模型中的RBFN模型能使算法的局部搜索能力增强，从而提高算法的多样性；HE-OMOPSO在ZDT4中的SP值差于其他测试函数的SP值，但是与单个Kriging代理模型算法相比，多样性较好，说明异构集成模型与单个代理模型相比，能够获得更好的局部搜索优化，增强算法处理不确定信息的能力，从而提高算法的多样性。

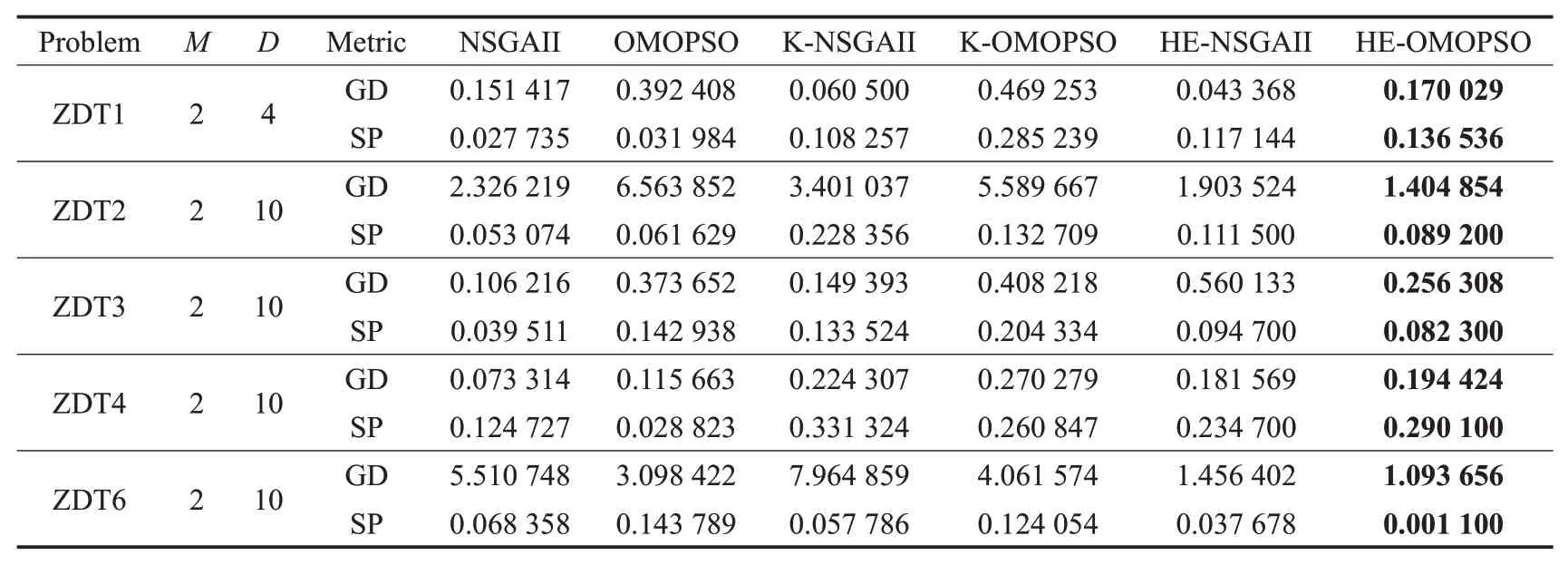
表2 不同测试方法的GD和SP平均值Table 2 Average value of GD and SP of different test methods

表3 不同测试方法的GD和SP标准偏差Table 3 Standard deviation of GD and SP for different test methods

表4和表5的实验结果表明，与ZDT4和ZDT6相比，本文所提方法在ZDT1、ZDT2和ZDT3中的优势更明显，这是因为ZDT4和ZDT6比ZDT1、ZDT2和ZDT3更复杂，并且这种复杂性使代理模型更难于适应真实函数。因此，ZDT4和ZDT6中的代理模型精度相对较低，这导致HE-OMOPSO算法性能较差。在求解ZDT1函数时，HE-OMOPSO和HE-NSGAII的HV值与NSGAII和OMOPSO的HV值相接近，这是因为ZDT1是低维问题，异构集成代理模型可利用较少的样本点构建更精确的代理模型，在提高收敛速度的同时能较好地逼近Pareto前 沿；与K-NSGAII和K-OMOPSO相 比，HEOMOPSO获得的HV值较好。对于ZDT2和ZDT3高维问题，HE-OMOPSO所获得的解在收敛性和多样性方面均劣于NSGAII和OMOPSO所获得的解，而HEOMOPSO所获得的解在收敛性和多样性方面略优于HE-NSGAII；HE-OMOPSO的HV值与K-NSGAII和KOMOPSO相比，收敛性和多样性较好，这是由于Kriging模型不适合高维问题，构建的代理模型精度和准确率较差，而HE-OMOPSO因为加入了RBFN模型，形成了异构集成代理模型，用于弥补Kriging的不足，因此获得的非支配解更接近于真实的Pareto前沿。由于ZDT4和ZDT6函数的复杂性，导致HE-OMOPSO算法性能较差，但是HE-OMOPSO获得的HV值与K-NSGAII和KOMOPSO相比，综合性能较好，说明HE-OMOPSO构建的异构集成代理模型在精度和效率方面优于单个代理模型。

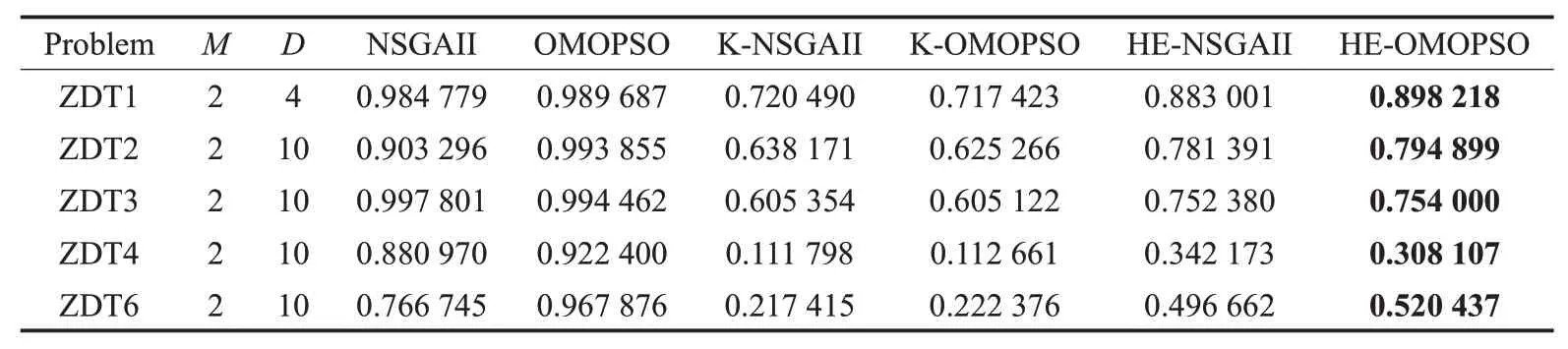
表4 不同测试方法的HV平均值Table 4 Average HV of different test methods

表5 不同测试方法的HV标准偏差Table 5 HV standard deviation of different test methods

需要注意的是，在每次迭代中，将在HE-OMOPSO中解决由Kriging模型和RBFN模型构成的近似多目标优化问题，因此，新方法对数值函数的计算时间成本比常规OMOPSO方法和NSGA-II方法要大。但是对于计算量大的多目标优化问题，通常需要几十个小时甚至更长时间来执行目标函数的仿真，因此可以忽略通过处理Kriging模型和RBFN模型而花费的时间。HE-OMOPSO的实际仿真成本要比所比较的算法少得多，因此，在解决昂贵的多目标优化问题时，HE-OMOPSO的整体计算成本要比传统的OMOPSO方法和NSGA-II方法好得多。

4 结语

本文提出了使用异构集成代理辅助多目标粒子群优化算法来解决耗时的多目标优化问题，将所提出的方法与HE-NSGAII、K-OMOPSO、K-NSGAII、OMOPSO和NSGAII进 行 了 基 准 测 试 函 数ZDT1、ZDT2、ZDT3、ZDT4和ZDT6的比较，使用GD、SP和HV三个指标来评估算法的性能。实验结果表明，本文所提出的方法获得的非支配解分布良好，并且解的均匀性不比传统的优化算法获得的解差。尽管提出的方法在ZDT4上的性能较差，这是因为目标函数难以拟合（模型精度差或目标函数的复杂性），但可以用更少的实际适应度函数评估生成更好的近似值。因此，与传统的优化算法相比，所提方法的计算成本更低，并且算法的搜索能力也令人满意，对于昂贵的多目标优化问题非常有效。未来的工作将进行代理模型的管理优化并用具有两个以上目标的问题来测试所提的方法。