基于DWT和生成对抗网络的高光谱多光谱图像融合
孙佳敏,宋慧慧
(南京信息工程大学 自动化学院,江苏 南京 210044)
0 引言
光谱图像存储了被观测场景的不同光谱特征,广泛应用于军事监视、环境气候监测和空间观测等领域[1-2]。通常,光谱图像主要分为2类:高光谱(Hyperspectral,HS)图像和多光谱(Multispectral,MS)图像。HS图像通常包含数百个光谱波段,具有很高的光谱覆盖率,可以准确地识别地面上的物质和物体;MS图像通常具有较高的空间分辨率。低空间分辨率的高光谱(Low Spatial Resolution Hyperspectral,LRHS)图像与高空间分辨率的多光谱(High Spatial Resolution Multispectral,HRMS)图像融合具有重要意义。
LRHS和HRMS图像融合大致可以分为2类:传统方法和深度学习方法。传统方法包括基于矩阵分解的方法和基于张量的方法等。Yokoya等人[3]提出基于耦合非负矩阵分解(Coupled Nonnegative Matrix Factorization,CNMF)的图像融合算法,求解LRHS图像的端元矩阵和 HRMS图像的丰度矩阵,将求得的端元矩阵和丰度矩阵相乘得到高分辨率的融合结果。与基于矩阵分解的方法不同,基于张量分解的方法通常将HS图像看作一个三维张量,高空间分辨率的高光谱(High Spatial Resolution Hyperspectral,HRHS)图像被分割成若干图像块,对图像块聚类,划分为对应的图形块集合。基于深度学习的方法在计算机视觉领域取得了巨大成功,在遥感图像处理中也得到了广泛应用[4-11]。基于深度学习的方法在复杂的非线性关系表示和高层次图像特征提取方面具有优势,其结果的准确性通常优于一些传统方法。虽然这些方法在LRHS和HRMS图像融合中取得了优异的性能,但如何有效地在空间和光谱之间传递信息仍然是一个挑战,对于提高融合图像的质量至关重要。
受文献[12]的启发,本文提出了一种基于离散小波变换(Discrete Wavelet Transformation,DWT)[13]和生成对抗网络(Generative Adversarial Networks,GAN)[14]来融合LRHS和HRMS图像的模型,包括一个生成器网络和一个判别器网络。在生成器网络中,首先使用设计的DWT下采样模块替换部分卷积层,以减少参数量,在较小的训练数据集上具有较好的性能,避免了模型冗余带来的过拟合问题,而且DWT保留了图像和特征映射中的频域信息,更有利于纹理细节的恢复。此外,结合上采样模块和跳跃连接可以获得多层特征信息。其次,在对LRHS图像上采样重建的过程中融合多尺度的HRMS图像信息。生成器的输出是融合重建的HRHS图像。判别器网络以融合重建HRHS图像、真值HRHS图像作为输入,进一步增加了生成图像的真实性效果。网络的损失函数由均方误差损失、对抗损失和焦点频率损失[15]组成。
1 方法
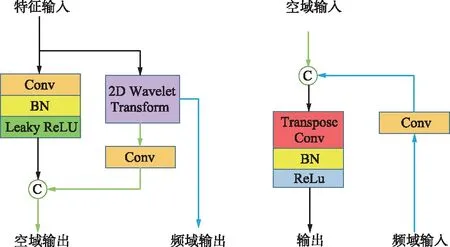
理想情况下,融合重建的HRHS图像应该与HRMS图像具有相同的空间分辨率,与LRHS图像具有相同的光谱分辨率。由于缺乏真实的HRHS图像作为参考图像,本文采用广泛使用的Wald协议[16]。根据Wald协议,卫星直接获取的HS图像作为HRHS图像。LRHS和HRMS图像分别通过对HRHS图像进行模糊下采样和等间隔抽样获得。假设XL∈Rw×h×K表示具有K个波段数的w×hLRHS图像,XM∈RW×H×k表示具有k个波段数的W×HHRMS图像(w 1.1.1 生成器网络 生成器网络结构如图1所示,包括特征提取和融合重建两部分。 特征提取部分使用卷积块结合DWT以减少参数数量,避免模型冗余带来的过拟合问题。DWT可以将输入的特征图分解为低频分量和高频分量,保留了图像和特征映射的频域信息,更利于纹理细节的恢复。在融合重建部分,为了充分利用HRMS图像的空间信息,采用在逐步上采样过程中与多尺度的HRMS图像融合的方式。LRHS图像经过特征提取后,通过多次亚像素卷积上采样,逐步放大到与HRHS图像相同的空间分辨率。在融合HRMS图像之前,使用1×1卷积将HRMS图像的通道进行扩展。为得到多个尺度的HRMS图像,使用MaxPooling对长和宽进行缩放。在多次亚像素卷积上采样过程中执行上述过程,实现高光谱特征图与不同尺度的HRMS图像相加融合。以放大倍数为4为例,XL∈R32×32×K经过特征提取和一次上采样后得到XL1∈R64×64×Z,XM∈R128×128×k经过1×1卷积和MaxPooling后得到XM1∈R64×64×Z,XL1与XM1相加后进行第2次上采样,与经过1×1卷积的XM相加后送入最终的3×3卷积中,重建得到XH∈R128×128×K。 图1 生成器网络结构Fig.1 Architecture of generative network 近年来,小波变换与深度学习相结合得到了广泛应用[12]。DWT将图像分解为低频子图和高频子图,能够提供优异的时频局部化特征信息,具有提取图像的边缘、细节信息的优势,可以在特征提取过程中全面地利用图像的信息。特征提取部分使用了多层金字塔式卷积块结合DWT的方法,如图2所示,自下而上,从粗到细,通过卷积下采样和转置卷积上采样得到多层的特征信息,在下采样的同时进行二维DWT,将特征分解为低频信息和高频信息,在每个特征尺度上通过跳跃连接来传递高低频信息。 图2 DWT模块结构Fig.2 Architecture of DWT module DWT下采样模块和DWT上采样模块如图3所示。在DWT下采样模块,DWT将输入的特征图分解为低频分量和高频分量。低频分量与卷积输出连接作为空域输出继续向下一个尺度传递,并且通过跳跃连接将低频分量和高频分量输入到DWT上采样模块中。不仅从多个尺度学习了空域和频域信息,而且通过跳跃连接保留了更多的纹理细节。 图3 DWT下采样模块和DWT上采样模块Fig.3 DWT down-sampling module and DWT up-sampling module 本文使用二维Harr小波变换,二维DWT过程如图4所示。输入一张图像,经过二维DWT后得到4个子带A,H,V,D,分别对应低频信息、水平高频信息、垂直高频信息和对角高频信息。 图4 二维DWTFig.4 Two dimensional discrete wavelet transform 1.1.2 判别器网络 为了区分真实的HRHS图像和融合重建的HRHS图像,本文训练了一个判别器网络。网络结构如图5所示。真值图像和融合重建图像作为输入,网络包含7个卷积层、8个Leaky ReLU层、6个BN层、2个Dense层和Sigmoid层,最终的Sigmoid激活函数输出真假样本的概率值。 图5 判别器网络结构Fig.5 Architecture of discriminator network (1) 均方误差损失 给定融合重建后的HRHS图像和对应的真值图像,均方误差(MSE)损失记为: (1) (2) 对抗损失 为了使得到的融合图像更趋向于真值图像,可优化如下对抗损失,使输出的真假概率趋同,对抗损失的定义是所有训练样本的判别器概率D(G(IL,IM))之和: (2) (3) 焦点频率损失 在损失函数中引入了焦点频率损失[14]LFFL,允许模型通过对容易合成的频率分量进行降权来自适应地聚焦于难以合成的频率分量,从而补充已有的空域损失,减少由于神经网络固有偏差造成的重要频率信息的损失,即: (3) (4) 总损失 将均方误差损失、对抗损失和焦点频率损失结合在一起来监督网络的训练,即: Ltotal=LMSE+LADV+αLFFL, (4) 式中,α=0.001为超参数。 为了验证本文方法的有效性,选择了3个典型数据集进行实验,并和8个最新的融合算法进行比较。 (1) 均方根误差(Root Mean Squared Error,RMSE)可以比较融合图像和真值图像之间的差异,其定义为: (5) RMSE的值越小,融合图像的质量越好。 (2) 峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)评价各波段的重建质量,是信号的最大功率与残差功率的比值。第l个频段的PSNR定义为: (6) (3) 相对全局误差(Erreur Relative Globale Adimensionnelle de Synthèse,ERGAS)[17]提供融合数据质量的全局统计度量,最佳值为0,其定义为: (7) (4) 光谱角制图(Spectral Angle Mapper,SAM)[18]通常用于量化每个像素处的光谱信息保留量,其计算式为: (8) 本文使用了3个数据集(PU,PC,Botswana)来验证所提出的基于DWT的GAN用于高光谱多光谱图像融合的有效性和泛化能力。 (1) Pavia University(PU)数据集是由反射光学光谱成像系统(ROSIS)传感器于2003年在意大利PU上空获得的。在该数据集共有103个波段,覆盖的光谱范围为0.43~0.86 μm,间隔为10 nm,每个波段的图像大小为610 pixel×340 pixel,空间分辨率为1.3 m。 (2) Pavia Center(PC)数据集是由PU数据集的相同Hyperion传感器以与PU数据集相同的空间分辨率获得的。它比波段数为103的PU数据集少一个波段。每个波段的图像大小为1 096 pixel×1 096 pixel,远远大于PU数据集。 (3) Botswana数据集是由NASA EO-1卫星的Hyperion传感器于2001—2004年在Botswana Okavango Delta上空获得的。Botswana数据集共有242个波段,覆盖的光谱范围为0.4~2.5μm,光谱间隔为10 nm。去除噪声波段后,剩余的145个波段保持不变,每个波段的图像大小为1 476 pixel×256 pixel,空间分辨率为30 m。 对于3个数据集,裁剪中心128×128区域作为测试图像,其余区域用于训练。使用步长为2的128×128滑动窗口从训练区域中提取图像作为真值HRHS图像。为了获得LRHS图像,本文使用4倍比率对HRHS图像模糊下采样,模糊核为5×5的高斯核,标准差为2。HRMS图像由位于HRHS图像中的5个图像等间隔组成。 选择CNMF[3]和基于张量分解(LTTR)[19]两种传统方法以及TFNet[20],ResTFNet[20],SSFCNN[21],ConSSFCNN[21],MSDCNN[22]和SSR-NET[23]六种深度学习方法与本文方法做比较。对于传统方法,除数据处理外,所有参数均设置为与原始文献相同。对于所有的深度学习模型,其输入和输出的通道数都是与所使用的数据集相适应的。在训练网络时使用Adam优化器,β1=0.9,学习率设置为10-4,批量大小16。此外,所提出的方法用Pytorch实现,并在单个GeForce GTX 2080Ti显卡上运行。 将本文方法与几种最新的融合方法进行了比较,包括CNMF[3]、LTTR[19]、基于深度学习的方法TFNet[20]、ResTFNet[20]、SSFCNN[21]、ConSSFCNN[21]、MSDCNN[22]和SSR-NET[23]。TFNet和ResTFNet是双流网络,分别对空间特征和光谱特征进行编码,然后利用空间特征和光谱特征的融合来解码HRHS图像。与TFNet相比,ResTFNet中增加了跳跃连接。SSFCNN和ConSSFCNN使用LRHS和HRMS图像的直接级联预测HRHS图像。MSDCNN基于残差学习和多尺度特征提取。SSR-NET对空间边缘损失和光谱边缘损失2种损失进行了优化,这2种损失是专门为空间和光谱恢复设计的。与传统方法相比,基于卷积神经网络(Convolutional Neural Networks,CNN)的方法性能更好,因为CNN可以自动学习高层次特征。其次,CNN的高度非线性对于在空间域和光谱域上模拟LRHS和HRHS图像之间复杂的非线性关系具有很大的潜力。 上述所有方法的实验结果如图6~图8所示,其中“GT”代表真值图像。第一行显示了融合的HRHS图像的R-G-B图像(67-29-1波段),第二行显示了融合的R-G-B图像与真值R-G-B图像之间的差异图像,这些图像经过伪彩色技术处理,显示了从融合重建的HRHS图像中选择的R-G-B图像以及融合R-G-B图像与相应的真值R-G-B图像之间的差异图像。结果表明,LTTR的融合性能较差,光谱失真明显,图像模糊。与LTTR相比,CNMF成像效果更好,图像更清晰、逼真。对于基于深度学习的方法,生成的图像质量普遍较高。然而,在MSDCNN的结果中发现了明显的颜色失真。与其他方法相比,ConSSFCNN的融合图像更加模糊。与TFNet,ResTFNet,MSDCNN,SSFCNN和SSR-NET的融合效果相比,本文方法可以获得更好的融合重建结果。 (a) CNMF (a) CNMF (a) CNMF 上述方法在3个测试数据集上的平均定量结果如表1~表3所示。最好的分数被标记为红色,第二的分数被标记为蓝色。 表1 不同方法在PU数据集上的融合结果 表2 不同方法在PC数据集上的融合结果 表3 不同方法在Botswana数据集上的融合结果 可以看出,对于所有4个评价指标,本文所提出的基于DWT的GAN取得了最好的性能,并且具有明显的优势。总体而言,本文所提方法在PU,PC和Botswana三个数据集上的融合性能最好。传统的CNMF和LTTR方法的性能比深度学习方法要差。在深度学习方法中,本文方法具有更优的性能。 本文提出了一种基于DWT和GAN的方法用于高光谱多光谱图像融合。与现有的基于CNN的方法不同,首先利用DWT帮助网络获得更多的频域信息,同时可以减少参数数量,然后充分利用多光谱图像的空间信息,并且在训练中加入焦点频率损失,缩小频域差距。最后利用生成对抗网络的对抗训练特性,生成更加真实清晰的高分辨率高光谱图像。大量实验结果表明,本文方法在高光谱多光谱图像融合方面具有很好的性能。由于实验是在模拟的HRMS和LRHS图像上进行的,因此不能确定本文方法是否适合实际应用,今后将在真实图像上测试其性能。1.1 网络设计




1.2 损失函数


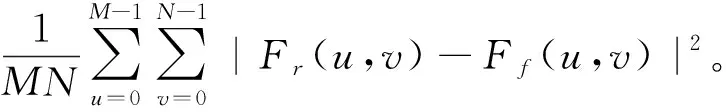
2 实验
2.1 评价指标




2.2 数据集
2.3 实验细节
2.4 性能比较






3 结束语

