基于PID控制的同步发电机励磁控制优化
韩雨晴,王致杰
(上海电机学院,电气学院,上海 201306)
0 引言
同步发电机励磁控制系统是同步发电机控制系统的焦点。同步发电机励磁控制在改善电力系统的稳定性方面具有十分重要的意义,因此同步发电机励磁控制始终受到学术界的广泛关注。通过多年的探索和实践证明,实现对于同步发电机励磁的合理有效控制,是实现整个电力系统的稳定和运行所需的最有效方法,因此,我们有必要针对发电机励磁控制系统的各种控制方法进行相应的研究。
发电机励磁控制系统的控制方法有很多,但实际控制中应用最广泛的控制方法还是 PID控制,PID控制是发展最早,迄今为止工程控制中应用最普遍的控制策略之一。自动调节控制系统如今也覆盖社会生产生活的方方面面,包括生物、电子、机械或政治经济领域,是工程控制领域里应用最广泛的系统之一。逐渐发展起来的控制理论以及方法很多基于传统的PID控制,随着科技的发展,实际控制过程中有大多数仍然采用 PID结构,并且许多最新出来的控制方式都是基于PID控制。
在许多控制方法中,简单的操作原理反而拥有更高的控制效果,并且易于实现。PID控制的适应性很强。对于非线性和时变系统来说,也可以对其实行一定的简化操作,转变成线性和非时变的一个系统。
因此本文对PID励磁控制系统进行了设计分析,运用PID参数整定原则选取到合适的PID控制参数,在 simulink 环境下创建了带 PID 控制和不带 PID 控制的励磁控制系统仿真模型,在相同的阶跃信号输入下对仿真结果进行对比,为使用PID控制提供了数据支撑。
1 同步发电机励磁控制系统建模
1.1 同步发电机励磁控制系统组成
同步发电机的励磁控制系统可以由下图 1来表示。
从图 1中可以看出初始是由发电机发出电压,电压的大小用Ug来表示,发出的电压经过电压互感器,用来测量Ug的大小,测量出来的大小与给定的电压Uref进行比较,得到偏差电压Uerr,其 Uerr偏差电压还需要通过电压调节器(AVR)对电压进行调节。由于发电机对设备或者蓄电池供电时,都会要求其输出的电压稳定,输出电压的稳定即通过调节电压的环节进行电压的调整[1]。偏差值进入自动电压调节器的增益部分进行分析和计算,最后通过励磁器的功率增益部分调节发电机的励磁电路。
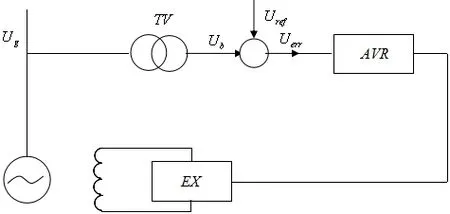
图1 励磁自动控制系统组成框图Fig.1 block diagram of the composition of the excitation automatic control system
1.2 同步发电机建模
由于同步发电机结构复杂且包含的变量众多,现创建分析发电机励磁控制系统所用的传递函数,故发电机的传递函数可以表示为:

式(1)中,KG为发电机的放大倍数;TG为时间常数。
1.3 电压测量比较单元建模
当同步发电机完成输出到输入转化的过程当中,对于整流滤波可能会有一些延时,此时,它可以用一阶惯性环节来表示,传递函数可以表示为:

式(2)中,KR为电压传感器的输入以及输出的常数;TR为滤波回路的时间常数。
1.4 综合放大单元建模
综合放大单元也可以近似为一阶惯性,传递函数可以表示为:

式(3)中,KA为移相触发及功率放大单元的放大系数;TA为移相触发及功率放大单元的时间常数。
1.5 功率放大单元建模
由于晶闸管的运行是间歇性的,有时间滞后。功率放大器单元也可以被认为是一阶惯性环节。因此传递函数可以近似写成:

式(4)中,KZ为功率放大单元系数;TZ为功率放大单元的时间常数。
1.6 同步发电机励磁系统建模
同步发电机励磁控制系统的总框图可用图 2来表示。
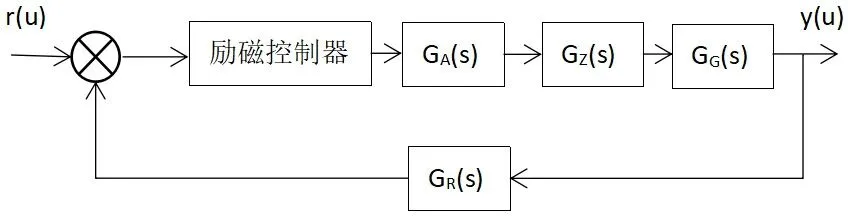
图2 励磁控制系统总传递函数模型Fig.2 total transfer function model of excitation control system
2 常规PID励磁控制器设计
将偏差的比例(P)、积分(I)和微分(D)通过线性组合构成控制量,对被控对象进行控制的控制器被称为PID控制器。模拟PID控制算法和数字PID控制算法是PID控制算法中两种不同类型的算法,分类的依据是按照信号类型输入与输出的不同进行划分。
PID控制器是根据给定的输入值r(t)与现实的系统输出值y(t)之间的偏差e(t)得到下面的PID控制规律,并得到其传递函数:
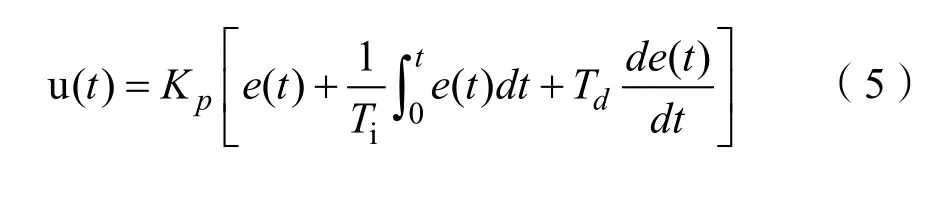
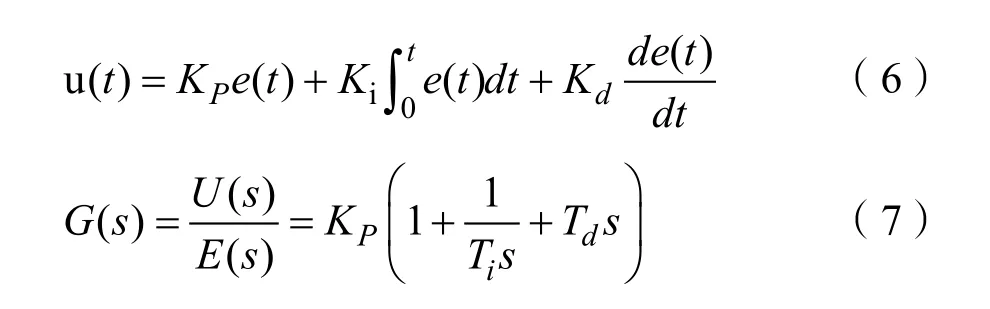
式(5)-(7)中:Kp为比例系数,Ki为积分系数,Kd为微分系数,Ti为积分环节时间常数,Td为微分环节时间常数。
2.1 模拟PID控制算法
模拟PID控制系统的原理图见图3。
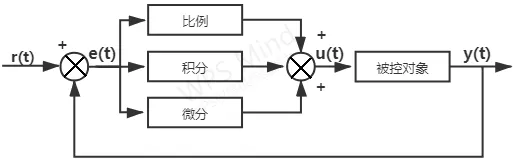
图3 模拟PID控制原理图Fig.3 analog PID control schematic
2.2 数字PID控制算法
随着时代的发展,实际应用与计算机常常有着紧密的联系,控制过程常常只能采用某一时刻的偏差量进行计算,离散化是数字控制中一项重要的步骤,综上,数字PID控制系统如图4所示。

图4 数字PID控制系统原理图Fig.4 principle diagram of digital PID control system
2.3 PID参数整定
PID参数的整定在励磁控制系统中起着至关重要的作用,合适的参数选取才能达到很好的控制作用,不合适参数的应用反而会适得其反,整定过程中方法与原则的选取很重要,在整定参数的过程中,系统的两大特性动态与静态性能与控制器的参数有着紧密的联系,它们之间会相互制约,需要进行大量的实验验证,多次进行调整,达到合适的控制效果为止。其中最重要的就是如何根据系统中出现的性能情况去调节比例、积分以及微分环节这三个环节的参数。
在保障励磁系统安全的情形下,初始参数的设置应相对稳妥,不应过大或过小,如比例系数的设置不宜过大,积分时间不宜过小等,避免系统出现异常情况,导致系统的不稳定。初始给定一个阶跃信号,系统空载运行,根据输出波形可以大致得到一些有关于励磁系统性能信息,比如超调量和调节时间,此时应该依据两者之间的关系,多次去调节PID的参数[6]。
若从响应曲线中观察得知系统不稳定,调节时间过长,与给定信号之间偏差较大,或者需要多次震荡环节才能达到相对稳定的状态,此时采取的方法是适当的使比例系数变小、使积分时间增大。在响应过程中,若响应曲线出现上升太慢,调节时间太长,应按对比上面参数调整规则进行反向调整。如果系统在减小误差的过程中调节速度较慢,可以使积分时间缩短。
在多次调节Kp和Ti之后,如果超调量仍然较大,应该在控制环节中加入适当的微分环节进行一定的控制,Ti逐渐增大,多次调节励磁控制器三个环节的参数,使系统的动态以及静态性能达到最优,即找到合适的控制参数。总之,PID参数的调整是个复杂过程,多个参数之间相互作用,相互制约,进行多次的尝试与调整,再进行观察分析是非常重要的。
3 系统仿真实验与结果分析
3.1 Simulink环境下建立同步发电机励磁控制系统的仿真模型
本节在第一章的基础上,采用各个单元简化的传递函数构建仿真模型,运行Matlab软件,打开Simulink工具包,创建同步发电机励磁控制系统模型。相关参数的选取如下:
同步发电机:TG=6.5s,KG=1.0;
电压测量比较单元:TR=0.04s,KR=1.0;
综合放大单元:TA=0s,KA=50;
功率放大单元:TZ=0.067s,KZ=1.0。
根据第一章同步发电机励磁控制系统建立的模型,以及上面相关参数的选取,搭建的仿真图如图5所示。
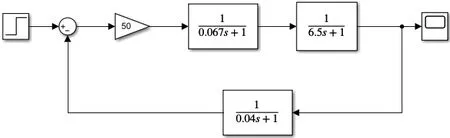
图5 励磁控制系统仿真模型图Fig.5 simulation model of excitation control system
3.2 Simulink环境下建立同步发电机PID励磁控制系统的仿真模型
在上面建立的模型的基础上增加PID调节环节,在Simulink环境下建立PID励磁控制系统仿真模型图,仿真模型图如图6所示,根据第二章中PID参数整定的规则多次实验,选取PID三个参数的数值为:Ki=0.3,KP=1.3,Kd=0.06。
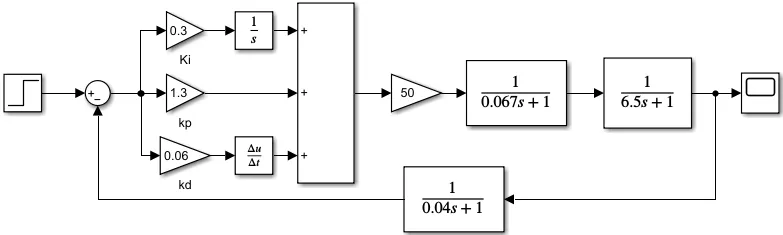
图6 PID励磁控制系统仿真模型图Fig.6 simulation diagram of conventional PID excitation control system
3.3 仿真结果比较分析
采用阶跃信号作为信号输入来模拟同步发电机的空载运行,并对无PID励磁控制系统以及带有PID控制的励磁控制系统进行仿真,仿真结果如图7和图8所示。
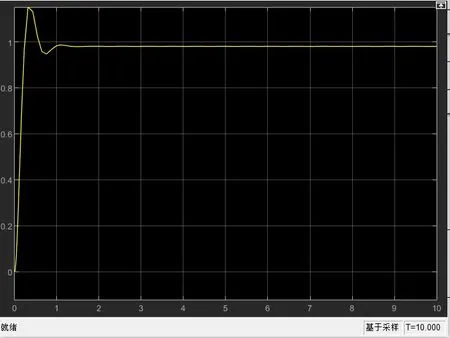
图7 无PID励磁控制系统仿真结果Fig.7 simulation results of PID-free excitation control system
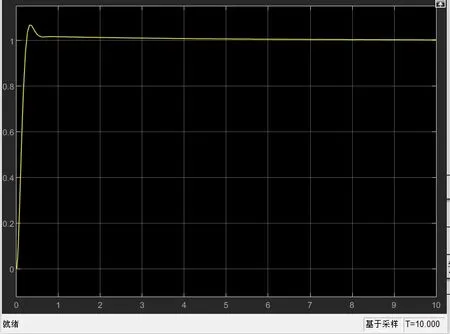
图8 PID励磁控制系统仿真结果Fig.8 simulation results of PID excitation control system
观察两个仿真图,从图7中发现在无PID的励磁控制系统中,出现了超调量并且较大,存在着一定的不稳定性并且稳定之后与给定阶跃信号之间也存在着一定的偏差。相较于无PID控制的励磁控制系统,加入PID调节后超调明显减小,并且更加稳定,调节时间与其相比也明显变小,提高了响应速度,并且稳定之后与给定值基本无偏差,说明励磁控制在加入PID控制之后可以明显提高系统性能。
4 结论
本文对同步发电机的励磁控制系统的PID控制器参数进行了优化,并对每个部分进行了建模,为后面的仿真奠定了基础,完成了PID励磁控制系统的设计,在 Simulink环境下进行了仿真实验,同时与无PID励磁控制系统在同样的条件下的仿真结果进行了对比分析,分析结果表明 PID控制下的励磁控制系统拥有良好的控制效果与可实施性。

