改进RRT*算法的智能车辆路径规划

赵港

改进RRT*算法的智能车辆路径规划

赵港

（长安大学 汽车学院，陕西 西安 710064）

RRT*算法是智能车路径规划的常用方法，但传统RRT*算法在汽车路径规划方面存在路径转折多、曲率波动较大等问题。针对这些问题，文章提出了一种改进RRT*算法，通过距离公式选取次级节点，同时添加路径转折点角度约束，从而达到限制最小路径段长度和减小路径曲率变化的目的。通过MATLAB仿真平台对改进的RRT*算法进行仿真验证。实验结果表明，该算法能够提高生成轨迹的平滑度，规划的路径更符合车辆在行驶过程中的轨迹特征。

路径规划；RRT*算法；角度约束

前言

随着现代社会汽车智能化程度的不断提高，路径规划已经成为智能驾驶汽车上的一个重要研究方面。路径规划主要目的是让目标对象在规定范围的区域内找到一条从起点到终点的无碰撞安全路径，是智能汽车完成驾驶任务的必要条件[1]。目前针对智能车路径规划的相关研究成果，大部分都是对移动机器人路径规划方法进行修改和调整得来的。路径规划算法主要有：基于图搜索的方法，以A*算法和D*算法为典型代表；基于采样的方法，以概率路图法（PRM）和RRT为代表；基于离散优化的方法；人工势场法：通过构建虚拟力场的方法，假设障碍物与车辆之前存在斥力作用，而目标点与车辆之前存在引力作用，通过计算合力的方法为车辆规划出一条可通过的安全路径。

文献[2]用复杂度低的度量函数以提高随机树的求解速度，嵌入Dijkstra算法进行优化，提高了算法的收敛速度。文献[3]通过目标导向思想对随机树中采样点的产生进行改进，引导随机树偏向目标点生长，降低了扩展的复杂度。文献[4]采用双向随机树和多棵局部随机树的探索与合并，增加引力分量，使双向随机树朝着各自目标方向生长，减少了算法的随机性。以上对于RRT*算法的优化并未考虑到生成轨迹的平滑性，因此，本文通过距离公式选取次级节点，避免因随机生成树的树枝过短而导致曲率大幅度波动的问题，并添加路径转折点角度约束，从而确保生成的轨迹平滑，满足智能驾驶汽车动力学约束。

1 RRT*算法

RRT*算法基于随即采样的方式来搜索空间，通过连接每个相邻的采样点构成随机生成树。根据地图信息得到障碍物的位置和状态信息，将全局配置信息记为，包含障碍物的空间记为obstacle，无障碍空间记为free，对象出发点记为init，目标点记为goal，RRT*算法原理如图1所示。

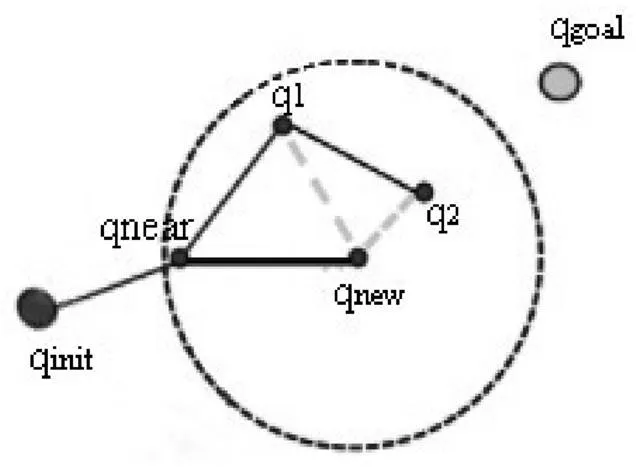
图1 RRT*算法原理图

（1）初始化随机树T，此时T中只有一个起始出发点init。

（2）在无障碍空间free中随机生成一个次级节点near，并且按照设定的扩展步长生成一个新的节点new，连接near与new，判断两点间的连线与obstacle是否冲突，此操作被称为碰撞检测，如果new通过碰撞检测，则将新节点new添加到随机树T上。

（3）在new的规定邻域内搜索满足要求的所有节点集合，图1中已用圆圈注明。此时将圆圈内其他点与near之间的代价函数作比较，若near到new的代价函数比通过1、2再到new的代价函数低，则将near与new进行连线。同时，还要对比从near出发到2的代价函数最低路线，若通过new到达2的代价函数最低，则将2的父节点更新为new，并更新代价函数。

（4）重复以上过程，直到直到达到迭代上限或找到目标点为止。通过对传统RRT*算法的算法流程可知，该算法按照随机采样的方式来寻找采样点，从而扩展随机树T。由于采样的随机性，会导致无障碍空间free上任意一点会被占据，而且采样点距离随机树T上点的距离存在不确定性，扩展的子节点随机分布将会导致以下问题：随机扩展中每个节点间连线长度具有随机性，从而导致连线段数过多，生成的路径曲率变化随机，很难满足智能汽车相关动力学约束的问题。

2 改进RRT*算法

2.1 最近次级节点的选择

RRT*算法在每次生成新的节点时都会根据距离公式选取距离随机树T上已知节点最近的点作为次级结点near。但是，如果选取两点间的最短距离过小，就会导致随机树T的树枝过短，生成的路径大幅度波动。因此，本文引入欧氏距离公式对当前节点pre与随机搜索到的节点rand之间的距离进行约束，规定两点间的最小距离不得小于设定的探索步长step，如果距离满足要求，就将新节点添加到随机树T上，否则重新生成新的节点进行判断。表1为改进RRT*搜索方法的算法伪代码：

表1 改进RRT*搜索方法的算法框架

次级结点qnear的选择策略 function Selection（） qrand=Sample_point（） distance=（qpre，qrand） if distance>step return qnear=qrand；end else return 2

2.2 路径转折点角度约束

RRT*算法生成节点具有随机性，导致生成的路径不平滑。在进行智能车辆路径规划时，没有考虑到汽车的动力学约束、最小转弯半径等因素，因此要尽可能控制路径的曲率范围。

图2为生成路径转折角度示意图。pre为当前节点，2为pre的父节点，rand为本次随机生成的节点。点pre与其父节点2连接构成的线段为，点pre与rand连接构成的线段为，两条线段构成的夹角为beta。当角beta越大时，生成的曲线越平滑，曲率波动越小。

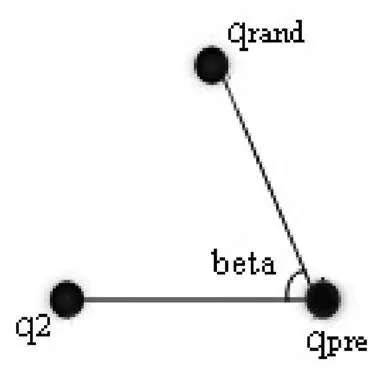
图2 路径转折点角度示意图

因此在RRT*算法中加入角度判别函数，只有当角beta大于90°时，才能将rand加入随机树T中。设2坐标为（1，1），pre坐标为（2，2），rand坐标为（3，3），此时线段的斜率1表示为：

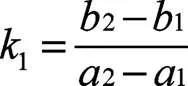
由式（1）和（2）可求得角beta的值：

3 仿真验证

为验证改进RRT*算法的性能，在Matlab仿真平台上进行试验。为了使改进后的算法可控，加入循环次数的限制。如果在规定循环次数内随机生成树T无法搜索到目标点goal，则显示算法返回失败，重新设置参数再次进行仿真验证。

设置大小为500×500像素的正方形仿真环境，被研究对象的初始位置坐标为[20,120]，目标位置的坐标为[490,490]，规定拓展步长为20，迭代次数最大值设定为10 000。分别采用原始RRT*算法和本文改进的算法进行路径规划，得到的仿真结果如图3所示。

图3 仿真结果图

智能汽车行驶环境如图3(a)和图3(b)所示，黑色区域为汽车行驶过程中的障碍物以及道路约束，空白区域为无障碍空间free。为验证改进RRT*算法的有效性，设置完全相同的仿真环境，经过随机生成树的扩展后，规划的路径为图3(a)和图3(b)中的曲线。

为分析改进RRT*算法的性能，在图3(c)给出两种算法路径规划的结果图。在初始位置附近，由于周围障碍物单一，对随机生成树的扩展影响较小，本文算法与原始RRT*算法所规划的路径基本重合。到达横坐标X为150附近，开始靠近第一个障碍物，原始RRT*算法所生成的路径曲率开始大幅度波动，轨迹间的连线角度接近90°。与此相比，本文算法生成的路径曲率变化较为平缓，轨迹间的连线角度接近160°。到达横坐标X为220之后，开始从两个障碍物中间通过，存在多个障碍物的干扰，可以看出两种算法规划的路径在此处有明显差异。原始RRT*算法由于没有路径转折点角度约束，生成的路径有尖锐的夹角(夹角小于60°），没有考虑到车辆的动力学约束。而本文算法生成的路径转折点最小角度为100°，考虑到了汽车在行驶过程中的轨迹特征。横坐标X为350之后，由于周围只存在一个障碍物，对算法规划路径的影响较小，本文算法与原始RRT*算法所规划的路径基本一致。

可以看出，相比于原始算法，经过改进后的算法规划的轨迹的曲率波动明显减小，轨迹也更平滑，能够更好的满足智能汽车在行驶过程中的运动学要求。

4 结束语

本文在现有RRT*算法的基础上提出了一种改进算法，通过引入欧氏距离公式对次级节点的选择进行限制，优化部分路径段的长度。同时，考虑到汽车行驶运动学的问题，通过设置转折点角度约束，提高路径平滑度。基于Matlab仿真平台对改进前后的RRT*算法进行仿真验证，结果表明，改进后的RRT*算法能够有效地降低路径规划的曲率波动，相比于比原算法，可以生成更为合理的路径。本文的仿真验证环节只在静态环境下进行，并没有考虑到动态障碍物，未来将考虑在具有动态障碍物的环境中进行路径规划，并能够根据障碍物的情况自适应的调整拓展步长，进一步提高该算法在路径规划方面的适应性。

[1] 刘琦.智能车辆驾驶行为决策与运动规划控制研究[D].西安:西安理工大学,2019.

[2] 梁中一,程方晓,魏巍.改进RRT～*路径规划算法[J].长春工业大学学报,2020,41(06):602-607.

[3] 韩丰键,邱书波,冯超,等.基于目标导向的双向RRT路径规划算法[J].齐鲁工业大学学报,2021,35(01):35-43.

[4] 施杨洋,杨家富,布升强,等.基于RRT改进的智能车辆路径规划算法[J].计算技术与自动化,2019,38(04):81-86.

Vehicle Path Planning Based on Improved RRT* Algorithm

ZHAO Gang

( School of Automobile, Chang'an University, Shaanxi Xi'an 710064 )

RRT* algorithm is a common method for intelligent vehicle path planning, but the traditional RRT* algorithm has many problems in vehicle path planning, such as path turning and curvature fluctuation. To solve these problems, this paper proposes an improved RRT*algorithm, which selects secondary nodes through the distance formula and adds the angle constraint of path turning point, so as to limit the minimum length of path segment and reduce the change of path curvature. The improved RRT* algorithm was simulated and verified by MATLAB simulation platform. Experimental results show that the algorithm can improve the smoothness of the generated trajectory, and the planned path is more consistent with the trajectory characteristics of the vehicle in the process of driving.

Path planning; RRT*algorithm; Angle constraint

A

1671-7988(2021)22-41-03

U495

A

1671-7988(2021)22-41-03

CLC NO.: U495

赵港，硕士研究生，就读于长安大学汽车学院车辆工程专业。

10.16638/j.cnki.1671-7988.2021.022.010