基于粒子群算法的磁悬浮列车控制参数优化

苗 欣，李言民，江守亮，金 浩

(1.中车青岛四方机车车辆股份有限公司，山东 青岛 266111；2.北京航空航天大学仪器科学与光电工程学院，北京 100191)

1 引言

高速磁浮列车以其与轨道无摩擦、低噪声等优势，目前已成为轨道交通领域内研究的热点。磁悬浮控制系统是磁浮列车的核心部分，其动态性能的好坏决定了列车系统的舒适性与安全性，因此对悬浮控制系统性能的优化就显得十分必要。悬浮控制系统性能的优化大致可分为控制系统结构优化与控制参数优化两个方面：控制系统结构优化包括电磁铁结构的优化、控制算法结构优化，如高温超导和电磁混合悬浮[1]、永磁电磁混合悬浮[2]等，通过改变电磁铁的物理结构提升悬浮控制性能；龙鑫林、佘龙华等在文献[3]提出的非线性控制方法，杨杰提出的悬浮系统的自扰控制算法方法[4]，又从控制算法结构上对悬浮控制系统进行优化。通过控制参数优化可以在悬浮电磁铁与控制器结构不变的情况下，提升控制性能，对于优化控制系统、指导调试车辆更具有现实指导意义。优化控制参数方法可以结合经典控制理论，如控制系统的随机线性二次最优原理[5]、零极点配置等方式，也可以依据时域或频域的控制性能指标，采用智能优化算法迭代求解最优参数组合，其实就等价为一定约束下的目标函数寻优问题，这种优化思想在各种控制领域得到广泛应用，如利用遗传算法实现多档位行星变速传动系统的动力学参数优化[6]，为降低齿轮传动误差，结合有限元计算，采用混沌蚁群优化算法进行优化[7]，利用改进多目标粒子群算法优化商用车的悬架系统参数，改善了汽车行驶的平顺性[8]，智能优化算法以其理论要求低，便于灵活运用的特点，被广泛应用于各类控制系统优化当中。

本文采用单电磁铁悬浮控制系统模型，通过改进的粒子群优化算法，使悬浮控制系统的传递函数与理想传递函数进行拟合，最终悬浮控制系统的动态响应特性与理想传递函数动态响应特性达到一致，从而优化了悬浮控制系统的轨道跟踪特性。

2 基于粒子群算法的参数优化

2.1 磁悬浮控制系统特性

磁悬浮列车的悬浮控制系统的最小系统为单电磁铁悬浮系统，一般而言，对于复杂控制系统设计，需要对系统进行降阶处理，减少模型自由度；另一方面基于Gottzein E提出“磁轮”[9]概念，TR系列的磁悬浮列车各悬浮点间耦合度大大降低，因此为便于分析磁浮列车的悬浮控制性能，一般建立单自由度磁悬浮控制模型图1。

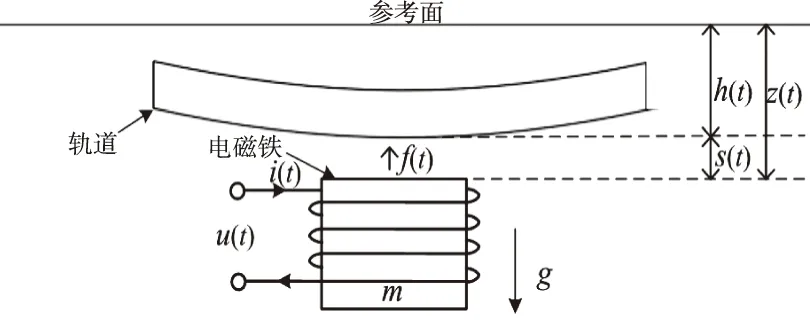
图1 悬浮控制系统

其中，u(t)为电磁铁电压、i(t)为电磁铁电流、m电磁铁的质量，f(t)为悬浮力，s(t)为电磁铁的测量间隙，h(t)为轨道面与参考面距离，z(t)为电磁铁与参考面距离。

系统的动力学方程

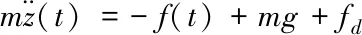
(1)

电磁力模型

(2)

轨道与电磁铁位置关系:

z(t)=h(t)+c(t)

(3)

电学方程

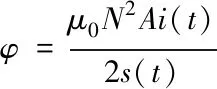
(4)

(5)

其中，fd为干扰力，φ电磁铁的磁链，R为电阻，A为电磁铁的有效面积，μ0为空气磁导率。

基于以上方程，得到线性化的传递函数如下[10]

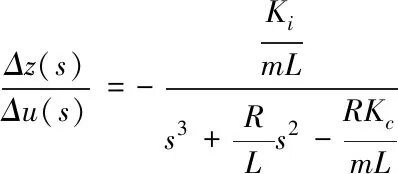
(6)

其中

根据劳斯定律，该系统为本质不稳定系统，因此需要进行闭环控制，引入间隙变化的微分量，增加特征方程的一次项，使系统变得稳定。

间隙变化的微分量一般可以通过如下两种方式获得：间隙的微分、加速度的积分。一方面，利用间隙传感器对间隙测量会对系统引进高频噪声，在微分环节的作用下，电磁铁会产生高频振动；另一方面加速度信号低频测量性能较差，在加速度积分的作用下，易产生零点漂移等，因此为避免以上两个缺点，构建二阶的观测器，综合利用两种传感器的信息对间隙变化率进行估计，其结构如下[11]图2所示。

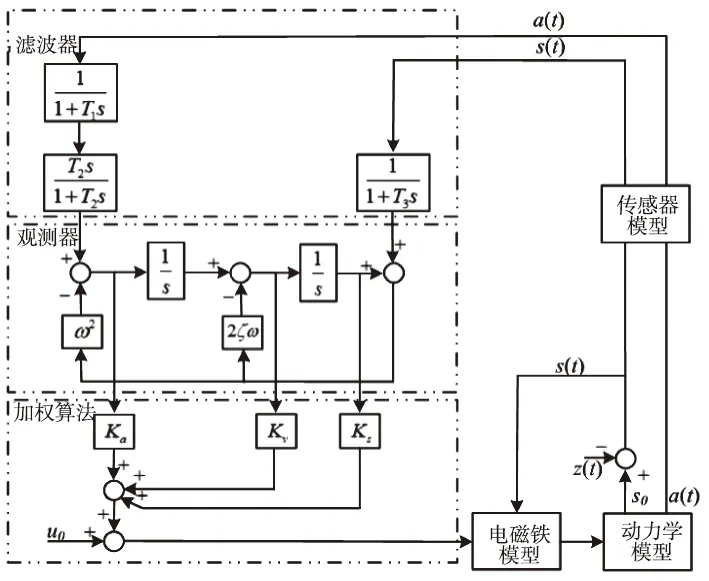
图2 悬浮控制系统模型

通过以上观测器可以得到估计后的加速度ao、间隙变化速度vo、间隙变化量so，并将以上的观测量加权求和，得到电磁铁的实时控制量，实现了带状态观测器的状态反馈控制。在稳定悬浮10mm时，以相对于参考面的轨道面变化Δh(t)为输入，电磁铁相对于参考面的位置变化Δz(t)为输出，可以得到线性化的传递函数

(7)

在系统稳定的前提下，对于Ka、Kv、Ks不同取值，该控制系统的带控制带宽、阻尼也会有所不同，从而决定了控制系统的性能。

2.2 磁悬浮控制参数优化原则

在高速运行时，为防止车辆撞击轨道、保证乘客安全，在较低频段的轨道面变化时，如弯道、梁跨、缓和曲线等，保证足够的稳定裕度，而对轨道错台、梁端转角等高频的轨道面变化不敏感。因此，对于25m长的高速磁浮的标准轨道梁，在列车最高时速600km/h下会存在6.7Hz左右的轨道梁特征频率，为保证列车安全性与舒适性，悬浮控制系统的带宽应需要设计为6.7Hz，同时要降低带宽内的谐振峰值，使带宽内的幅频特性较为平坦。

对于阻尼比ζ、无阻尼振荡角频率为ωn的二阶系统而言，其传递函数为

(8)

由图3、图4可知，当阻尼ζ=0.707时，对于5%的误差带，系统调节时间最短[12]；超调量为4.3%，相对较低;其自然频率即为传递函数的带宽，并且带宽内无谐振峰值，因此根据以上分析，以阻尼ζ=0.707、ωn=6.6Hz得到的理想系统，在保证响应能力的同时，超调量相对较小，具有很好的较好的综合性能，综上所述，可以得到如下的理想函数

图3 超调量(左)、不同误差带下调节时间(右)与阻尼关系

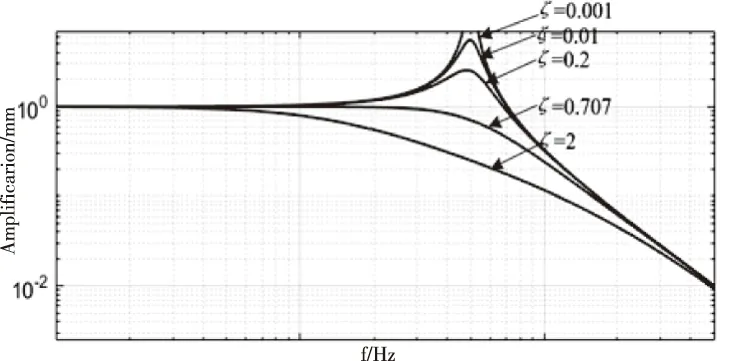
图4 不同阻尼比的幅频特性

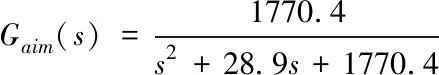
(9)

对于实际悬浮控制系统模型，可以通过迭代算法寻找Ka、Kv、Ks使得悬浮控制系统与理想系统性能近似，实现两个系统的近似，达到保证悬浮系统在指定带宽情况下，具有较好的动态性能。考虑到电磁铁悬浮控制系统是一个较强的惯性系统，具有典型的低通特性，因此可以得到如下结论：

1)低频带内Gaim(s)与Gmag(s)特性差别不大，幅频曲线都较为平坦，此时悬浮控制系统对缓和曲线、弯道具有较好的跟踪性。

2)中频带对系统的动态性能具有重要作用。

3)高频带内，由于实际系统的动态特性与Gaim(s)惯性作用特性一致，都具有大幅度的衰减特性。

因此，对于两个系统的拟合主要着眼于低频带末端以及中频带，为使两个系统的性能相近，以ωn为中心，设置拟合的频带为[ωn-Δωωn+Δω]，若按照一定原则保证两个系统在该频带内近似，就能实现控制系统与理想系统的动态特性拟合。

对[ωn-Δωωn+Δω]进行N点均匀等分，对于ωi频率下的理想系统的传递函数与悬浮控制系统的传递函数复数域的差值为

Δi=Gmag(s)-Gaim(s)

=|Gmag(jωi)|eφ(jωi)-|Gaim(jωi)|eφ(jωi)

(10)

对于[ωn-Δωωn-Δω]内所有的频率点，设置目标函数指标如下

(11)

该指标本质上是Δh(t)为输入、Δz(t)为输出的闭环控制系统与理想系统的奈奎斯特曲线拟合(如图5)，即在指定固定的频带内，使目标系统和悬浮控制系统该复数坐标系下拟合，就能确定闭环系统输入和输出的幅值相位关系，从而保证悬浮控制系统与目标系统动态行为上的一致。

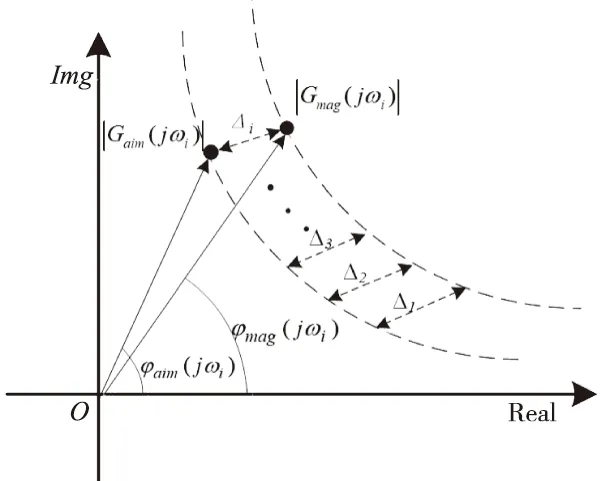
图5 系统奈奎斯特曲线拟合原理

此外，对于如果将悬浮控制系统的等价为二阶系统，那么Bode图上低频段等效的谐振频率和增益的峰值为

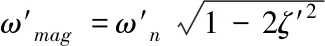
(12)

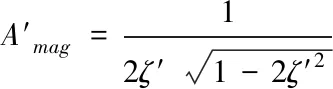
(13)

ΔA=|Aaim-Amag|→0

(14)

同时，为保证系统的带宽，设置带宽指标如下

Δω=|ωaim-ωmag|→0

(15)

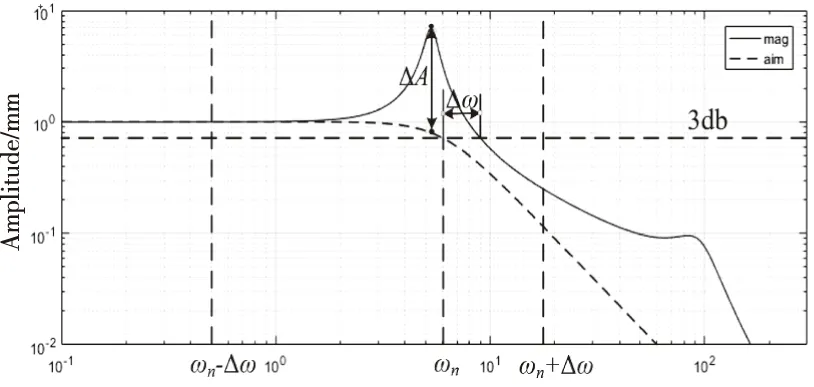
图6 ΔA、Δω指标

基于以上的分析，最终设置目标函数如下

J(Ka，Kv，Ks)=αΔd+βΔA+γΔω

(16)

其中α、β、γ为加权因子，随着Ka、Kv、Ks不同取值，J的值也会随之变化，通过一定的计算方法得到J的最小值，就可以找到最优化后的悬浮控制参数组合。

2.3 改进粒子群优化方法

粒子群算法是由J.Kennedy和R.C.Eberhart最早提出[13]，参考动物的群体性行为规律设计的智能算法，具有算法灵活调整、收敛速度快、原理简单的特点，在智能控制、函数优化等领域应用广泛[14][15]。

假设有N个粒子的群落，其中第k个粒子的位置可以用一个D维度的空间向量表示

xk=(xk1，xk2，…xkD)

(17)

对于每个粒子，每一次迭代移动的速度向量为

vk=(vk1，vk2，…vkD)

(18)

vk由有三部分组成

vk=ωvk-1+c1r1(xlocal-xk-1)+c2r2(xglobal-xk-1)

(19)

其中，ω为权重因子，vk-1为前一次迭代时的速度向量，c1、c2为学习因子，r1、r2为[0 1]之间的随机数，xlocal为第k个粒子的历史最优值，xglobal为全部粒子的历史最优值。

位置更新方程

xk=xk-1+vk

(20)

根据优化计算的指标要求，选取适宜的目标函数，经多次迭代后，即可找到参数xk的优化值。但是这种方式下，粒子在迭代初始寻优过程中，易进入局部最优值的情况，为减小进入局部最优的可能性，对速度的向量方程作如下改进

vk=ωivk-1+ci(xlocal-xk-1)+di(xglobal-xk-1)+eirxk-1

(21)

其中，权重参数ωi、ci、di、ei随着迭代次数增加的线性递减，r为[0 1]之间的随机数。

在迭代初期ωi、ci、di、ei相对较大，各个粒子在空间内运动比较剧烈，增强了全局收敛内能力，迭代晚期数值较小，保证了的局部收敛能力此外，由于随机因子r从粒子的自主学习和社会学习中剥离，使得粒子惯性更强，收敛更为快速。为尽量减少陷入局部最优的可能，可以采用试凑的方法，找到较为接近目标系统的一组参数x(Ka、Kv、Ks)，作为迭代计算的粒子初始位置，可置粒子边界范围

[(1-η)x(Ka，Kv，Ks) (1+η)x(Ka，Kv，Ks)]

其中，0.5<η<1为边界调整因子。

此外，在迭代优化中，需要设置判断系统稳定的边界条件，保证每个参数下系统特征根位于虚轴左侧，剔除使系统不稳定的控制参数组合。

2.4 仿真结果

基于以上分析，设计粒子群算法粒子的初始位置为x(Ka，Kv，Ks)=x(300、900、150000)，取带宽频率ωn=6.7Hz，Δω=6.3Hz，需要拟合的频带范围为[0.4Hz 13Hz]，其中[0.4Hz 6.7Hz]为低频带，以保证系统的低频特性，[6.7Hz 13Hz]保证系统的动态响应特性，以粒子数N=500，迭代次数为500进行迭代运算，优化后的粒子位置为x(174.57、1453.5、122589.3)，目标函数值、奈奎斯特曲线、闭环系统bode图的收敛过程如下。

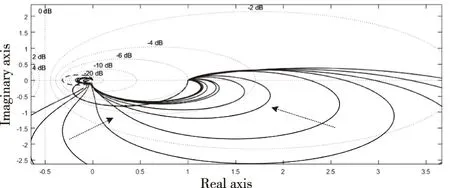
图8 系统闭环奈奎斯特曲线收敛过程

图9 系统幅频曲线收敛过程

如图7，从优化目标函数值的收敛过程来看，粒子群的初期收敛速度较快，具有较强的全局搜索能力，晚期的收敛过程较慢，保证了晚期的局部收敛精度。随着迭代进行，奈奎斯特曲线和bode图在固定带宽[0.4Hz 13Hz]内逐渐接近，谐振峰值逐渐减小，同时带宽逐渐靠近目标带宽，达到了控制目标。

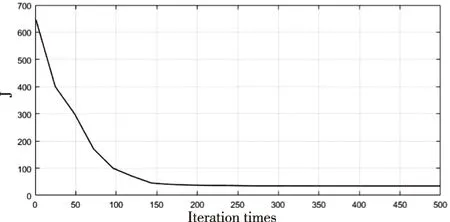
图7 优化目标值的收敛过程

3 硬件在环试验结果

dSPACE半实物仿真系统是由德国dSPACE公司研发的，是一种基于MATLAB/Simulink软件的控制系统开发及半实物仿真的软硬件实验平台，可以非常方便的结合MATLAB/Simulink进行半实物仿真。dSPACE实时系统拥有实时性强，可靠性高，扩充性好等优点[16]。采用SCALEXIO型号半实物仿真机搭建硬件在环的试验系统如图10。

图10 悬浮控制硬件在环试验平台

其中，工控机用于仿真模型的搭建，快速原型电路用于运行磁悬浮控制算法，SCALEXIO仿真用于运行电磁铁模型、列车动力学模型、传感器模型等，它们之间通过信号线连接形成闭环控制回路。

首先将系统模型各部分离散化，将控制算法通过Simulink的Embeded Coder工具包转换控制代码后运行在快速原型电路，然后在仿真机中编辑轨道不平顺激励，传感器模型测量间隙和加速度信号，通过线缆传输到快速原型电路中，快速原型电路的控制算法计算出控制电压，将该控制电压反馈到仿真机的电磁铁模型，电磁铁模型计算出悬浮力并作用到车辆动力学模型上，产生变化的间隙和加速度。

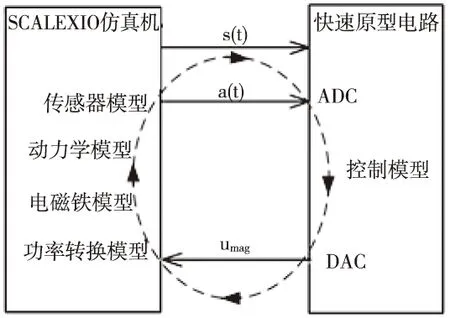
图11 硬件在环的拓扑结构

假定轨道梁挠度为5mm[15]，以典型的25m长轨道梁为例，设置4Hz、6.7Hz时的半正弦激励，并添加随机不平顺，分别模拟列车以350km/h、600km/h列车经过梁跨的情景，以验证控制参数优化方法的有效性，试验结果如图12。

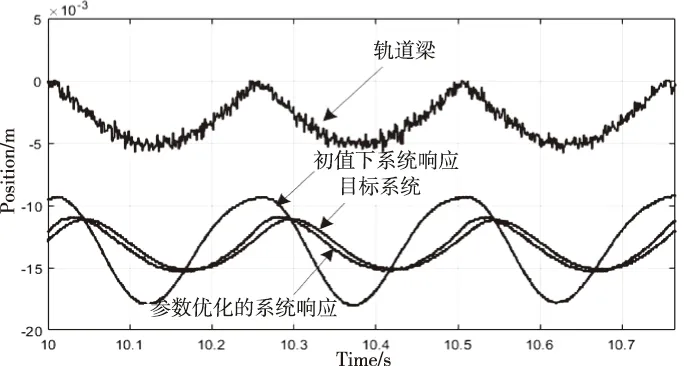
图12 4Hz轨道激励下的悬浮控制系统响应

如图12所示，当列车运行速度为350km/h，轨道激励为4Hz时，悬浮控制系统在初值参数的系统响应、优化参数后的系统响应、理想系统响应下的电磁铁振动的幅值分别为4.3mm、2.2mm、2.1mm。表明优化参数后的悬浮控制系统与目标系统动态行为相似，低频跟随性较好，能够较为理想地跟踪轨道。

如图 13列车速度为600km/h时，此时系统的轨道梁的激励频率为6.7Hz，悬浮控制系统在初值参数的系统响应、优化参数后的系统响应、目标系统响应下的电磁铁振动的幅值分别为4.2mm、1.6mm、1.4mm。初值参数下的悬浮控制系统，响应比较剧烈，由于悬浮电磁铁的具有较强非线性，电磁铁容易控制失稳或者与轨道吸死，而参数优化后的悬浮控制系统与理想系统响应近似，具有很好的跟随性，提高了列车舒适度和安全性。

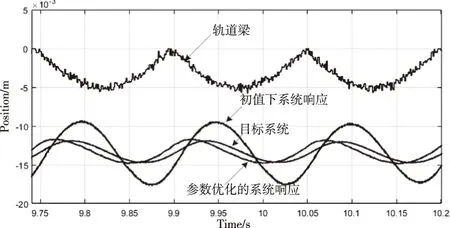
图13 6.7Hz轨道激励下的悬浮控制系统响应

如图14 对于8Hz及以上轨道激励，可以认为是悬浮控制系统需要抑制的轨道不平顺，系统此时不应跟踪轨道梁，初值参数下、优化参数下的悬浮控制系统与理想系统电磁铁振动的幅值分别为2.1mm、1.4mm、1.1mm。初值参数下的悬浮控制系统，阶跃响应振动剧烈，控制参数优化后的系统响应较为平缓，列车舒适度和安全性得到了提高。

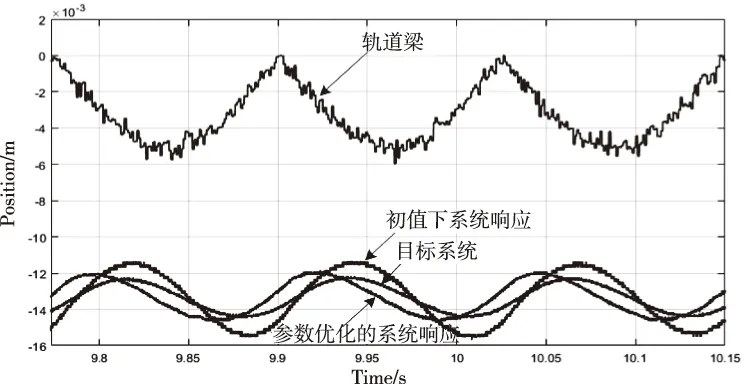
图14 8Hz轨道激励下的悬浮控制系统响应

磁悬浮列车系统在长期的运营当中，可能出现地基下沉等现象，会导致的轨道梁错台的产生，列车高速通过时，测量间隙的产生阶跃，引起悬浮控制系统振荡收敛，影响列车乘坐舒适度。

在仿真机中模拟5mm的轨道阶跃[17]如(图 15)，发现初值参数下、优化参数下的悬浮控制系统与理想系统电磁铁振动的超调量分别为37%、11%、4.8%。动态调节时间为分别为0.95s，0.3s，0.11s，因此优化后的控制参数在系统的稳定性、快速性都显著提高。

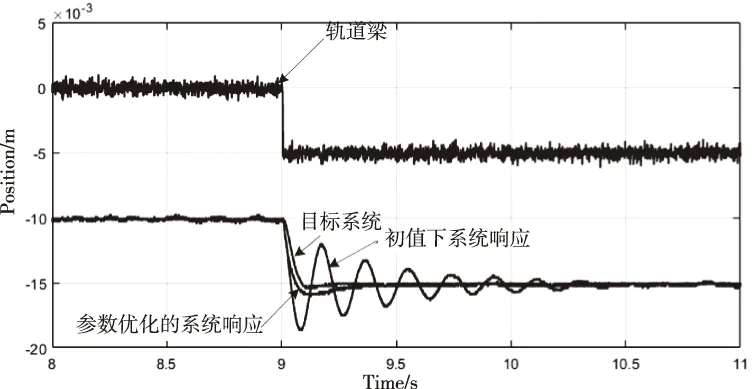
图15 5mm的轨道阶跃响应

4 结论

高速列车悬浮控制动态特性与控制参数关系密切，通过优化控制参数，使悬浮控制特性满足安全和舒适度指标更具有工程意义。针对目前时速600km/h磁浮列车尚未有试验线路的现状，本文首先确定理想拟合系统的传递函数，再通过粒子群算法使系悬浮控制系统与理想传递函数近似，通过搭建的半实物仿真系统，对悬浮控制参数进行了先期验证与参数优化，经半实物仿真验证，悬浮控制系统的快速性和平稳性得到了提高。

为提高拟合手段的精确性，对于指标函数的优化、加权因子等的设定是需要进一步研究的方向，此外考虑电磁铁的非线性等因素，提高整个模型的建模精度对参数优化方法的可靠性也有重要作用。