基于SWT和SVR的重力坝变形预测研究
李麒 朱光平
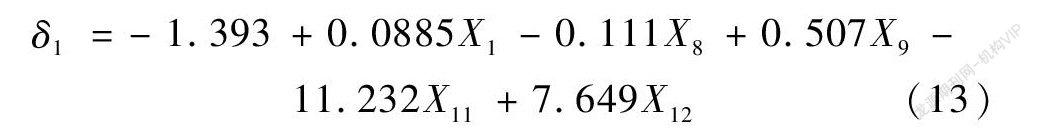
摘要:变形是重力坝安全状况的最直接反映,应用合理的变形预测模型可以对重力坝工作性态进行准确的监控及预警。利用Hampel滤波剔除原始变形信号粗差,通过平稳小波变换(SWT)获取变形信号多尺度分量,对比分析了不同阈值函数及阈值确定方法的去噪效果。针对预处理后数据及原始数据,分别采用逐步回归分析、BP神经网络和支持向量回归(SVR)建立变形预测模型,对比分析了各模型的预测效果。结果表明:SVR模型预测效果最好;经过预处理后的数据建模预测效果优于原始数据。
关键词:重力坝; 变形预测; 平稳小波變换; 阈值去噪; 支持向量回归
中图法分类号: TV642.3
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2021.11.028
0引 言
混凝土坝最主要的破坏形式是坝基滑动,因此坝体变形是其安全状况的最直接反映,也是国内外专家公认的最可靠指标[1]。有必要建立合理的重力坝变形预测模型,对重力坝工作性态进行准确的监控及预警。
目前,大坝常用的预测模型有多元回归模型、确定性有限元模型以及有限元与回归模型相结合的混合模型[2],这些模型有的泛化能力较差,有的计算量大。随着国内外学者对大坝变形预测模型研究的深入,神经网络、支持向量机、相关向量机等智能算法被逐渐应用到该领域[3-5]。受监测仪器、外部环境以及人为因素的影响,大坝变形监测数据不可避免地含有粗差及噪声,会影响后续的数据分析及预测模型的建立[6],然而目前很多研究均忽略了数据预处理的相关研究,导致得到的预测模型存在一定程度的偏差。
为了提高重力坝变形预测模型精度,本文利用Hampel滤波剔除原始变形信号粗差,并通过平稳小波变换(SWT)赋予低惩罚阈值去除噪声。考虑合理的环境影响因子,针对预处理后数据及原始数据,分别采用逐步回归分析、BP神经网络和支持向量回归(SVR)建立变形预测模型,并采用均方误差和拟合优度作为评判标准比较分析了各模型的预测效果。
1基本理论
1.1Hampel滤波
在大坝变形监测过程中,由于突发的不正常因素(如传感器噪声、信道干扰、处理过程失真、人为因素等)的影响,粗大误差的产生不可避免。粗大误差的测量值也可称为离群值,其不服从实测数据的统计分布规律[7]。当数据受到粗差污染时,会导致数据模型误差、模型参数估计错误和分析结果错误。因此,有必要对变形测量过程中的粗差进行识别和剔除以提高测量效果。在数据处理过程中,通常根据数据的位置和分散性来判断异常值。常用的粗差识别方法有拉依达准则、格雷布斯检验法、迪克逊检验法等,上述方法受数据分布和数量的限制,不能直接应用于数据处理[8]。然而,Hampel滤波法能够在不获取数据完整趋势的情况下判断粗差,具有良好的实时性和识别效果,因此成为在线粗差检测的较好选择。本文采用基于决策的Hampel滤波器进行粗差处理,其定义如下:
1.2平稳小波阈值去噪
大坝变形监测数据通常会受到高频噪声污染,从而影响后续数据分析和建模的精度,因此有必要对数据进行去噪处理。小波分析在时域和频域均具有良好的局部化性质,特别适用于非平稳信号的处理,因此本文采用小波分析进行时序数据去噪。
小波阈值去噪的基本原理是,通过小波变换将信号分解成不同尺度和分辨率的多个分量,其中噪声大多分布于高频分量,其小波系数幅值较小,而信号的一般趋势主要分布于低频分量,其小波系数幅值较大。通过选取合适的阈值,将小波系数小于阈值的部分去除过滤,剩余的部分重构后即为去噪信号[9]。小波分解在大坝变形监测数据去噪中的作用是仅去除高频分量中的噪声,尽可能地保留数据的低频成分。目前小波阈值去噪主要采用的是离散小波变换(DWT),会失去平移不变性并在重构时导致吉布斯振荡[10]。平稳小波变换省略了离散小波变换中的上采样和下采样过程,从而保证了不同小波分解水平下的子带大小相同,以便于最优子带阈值的选择。此外,SWT还可以在每个小波分解级别提供更精确的方差估计以识别噪声[11]。因此,本文采用SWT进行大坝变形监测数据的消噪处理。平稳小波阈值去噪的示意图如图1所示,主要包括3个步骤:① 平稳小波分解,选取合适的小波函数和最高分解层数N,计算信号s在每一层的小波系数;② 设定阈值,选择合适的阈值选取方法以及应用模式,对各层细节部分小波系数进行阈值处理;③ 信号重构,利用第N层的近似部分小波系数以及1~N层的阈值处理后各细节部分小波系数进行平稳小波逆变换(ISWT),重构得到原始信号估计。
2变形监测数据预处理
2.1工程概况
陆水枢纽混凝土重力坝坝顶上游侧布置有引张线自动化系统以监测坝顶的水平位移,共14个测点。此次选取坝顶中部6号测点在2014年1月至2016年11月期间的监测数据开展相关研究,规定水平位移下游方向为“+”,上游方向为“-”。为了减少粗差及噪声的影响,拟采用Hampel滤波结合平稳小波阈值去噪对采集到的变形数据进行预处理。
2.2粗差剔除
图3给出了该混凝土重力坝坝顶测点EX6水平位移实测过程线。由原始时间序列可以看出,大坝水平位移呈明显的年周期变化,另外,受外部环境或仪器自身影响,原始数据存在一定程度的缺失。首先采用滑动窗口(窗口大小为15)的中位数填充缺失值,然后对补缺后数据进行Hampel滤波(窗口大小为3),处理结果如图4所示,处于上下边界外的数据认为是粗差,采用窗口均值替代。由图4可知,原始序列在2014年3月25日及2016年6月1日处存在明显的异常值,经查,此时间段内上游水位、气温、降雨并无明显异常,很有可能是仪器不稳定导致的粗差。经过Hampel滤波后,原始序列各数据保持不变,仅粗差值被替代。需要说明的是,明显粗差值通过过程线可以直观识别,但是对于粗差较多的过程线以及传感器较多的情况,通过Hampel滤波可以实现粗差数据的自动化快速识别、剔除及补缺。
2.3平稳小波去噪
针对去粗差后的大坝变形数据,考虑到较小尺度下的小波变换能减小频率混叠现象[13],通过试验分析,选用正则性较好的db3小波对该序列进行3层分解,分解结果如图5所示。其中D1,D2,D3为时间序列的高频部分,A3为时间序列的低频部分。由图5可知,由于噪声的存在,高频部分振动较剧烈,通过对高频部分进行阈值处理,从而提取原始数据中的有效信号。经过计算,高、中、低惩罚阈值分别为0.092,0.055,0.049。表1给出了不同阈值确定方法下分别采用软阈值和硬阈值方式去噪后的均方根误差和信噪比。由表1可知,硬阈值函数处理效果普遍好于软阈值函数处理效果,低惩罚阈值在不同阈值函数下效果均最好,采用低惩罚阈值下的硬阈值去噪方式去噪效果最优,均方根误差仅有0.013而信噪比达到了40.48。
图6为大坝变形去粗差序列与去粗差后再去噪序列的对比图,由图6可知,经过平稳小波阈值去噪后,原序列变化趋势得到保留,仅高频噪音部分被抑制,去噪后数据线较为光滑。
3变形预测模型的建立
变形预测模型的建立对于大坝变形监控及预警意义重大。本节对经去粗差、去噪处理后的数据,分别采用逐步回归分析、支持向量回归机以及BP神经网络建立大坝水平位移预测模型,并对比分析了各方法的预测效果。
已有的坝工知识和变形监测数学模型表明,混凝土坝水平位移主要受上下游水位、温度和时效等因素的影响,考虑到下游水位数据缺失,本文建模仅考虑上游水位H。建立大坝位移预测模型时,考虑的环境因子主要包括:水压因子4个(H,H2,H3,H4),温度因子4个(观测日当天气温T,观测日前期1~7 d气温平均值T1-7,观测日前期8~30 d气温平均值T8-30,观测日前期31~60 d气温平均值T31-60),时效因子4个(t,In(t+1),t/(t+1),1-exp(-t),其中t=(观测日序值-基准日序值)/365,将这12个因子按顺序编号为X1,X2,…,X12。选取预处理后大坝水平位移数据的前80%作为训练集,后20%作为预测集,分别计算各模型预测值对应的均方误差MSE和拟合优度R2来检验预测效果。
经过数轮逐步回归分析计算,建立了坝顶水平位移统计模型如下:
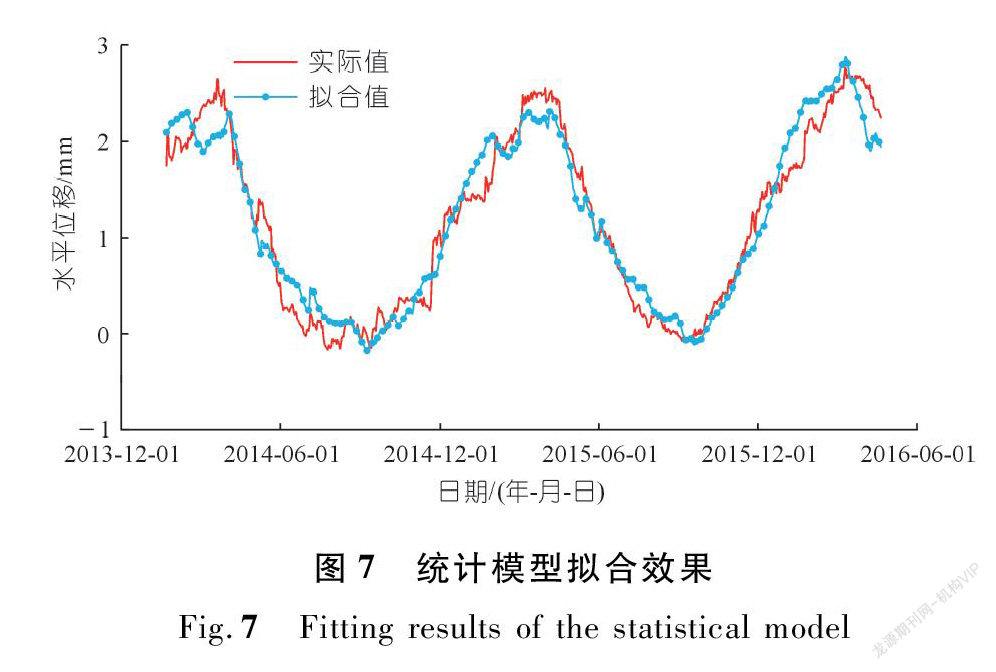
拟合结果如图7所示,统计模型的复相关系数达到96.57%,由此可知,经逐步回归分析所得统计模型的拟合效果较好,可用于后续变形预测。
考虑到各因子的物理意义及量纲有所不同,为了优化训练效果,在采用支持向量回归机建立预测模型时,首先将数据集归一化到区间[0,1],然后采用交叉验证和可变网格搜索法[14]确定惩罚系数C和宽度參数γ分别为0.031 25和0.25,根据文献的建议[15],系数ε一般取0.000 001即可。应用归一化后的学习样本集进行训练得到SVR预测模型δ,并依据此模型进行预测值检验。作为对比,同时采用BP神经网络法建立预测模型δ,网络输入层节点数为12,隐含层节点数为6,输出层节点数为1,网络学习的迭代次数设置为100次,学习率为0.01,训练目标的最小误差为0.001。
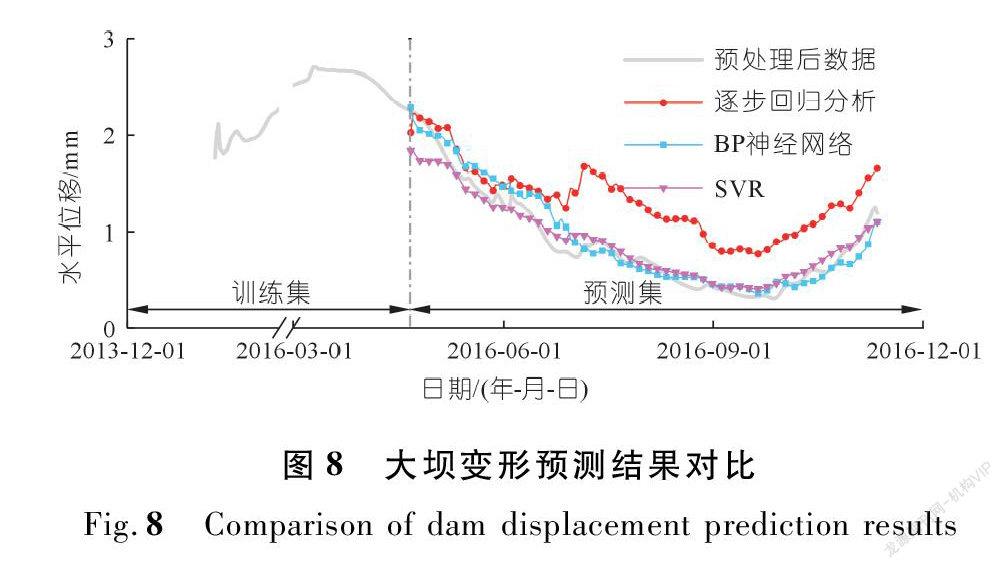
3种模型的预测结果如图8所示,对应的均方误差和拟合优度计算结果见表2。表2同时给出了仅根据原始数据建立的3种预测模型的预测效果。由图8可以明显看出,逐步回归分析得到的变形预测模型在2016年6月28日之前的预测效果较好,在该日期之后预测偏差相对较大,而SVR和BP神经网络预测结果均较优。根据表2给出的具体预测效果数据,SVR模型的预测结果相对于其他两种预测模型来说精度更高、适应性更好,该模型预测性能更优。同时,对比分析根据预处理数据与原始数据建立的3种预测模型的预测效果可知,经过去粗差及去噪可以在一定程度上提高模型预测精度。
4结 论
(1) 对于给定的大坝变形数据,采用低惩罚阈值下的硬阈值去噪效果最好。
(2) SVR模型的预测结果相对于逐步回归分析和BP神经网络模型来说精度更高,适应性更好,其模型预测性能更优。
(3) 经过去粗差及去噪处理后,变形预测模型的精度可以在一定程度上得到提高。
参考文献:
[1]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.
[2]顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006.
[3]屠立峰,王慧,顾微.基于GCS-SVM的大坝变形监测非线性预警模型[J].中国农村水利水电,2015(5):114-116.
[4]杜传阳,郑东健,陈敏,等.基于APPSO-RVM与APPSO-SVM的大坝安全预警模型的应用比较研究[J].水电能源科学,2015,33(3):45-49.
[5]黄世秀,洪天求,高飞.基于小波消噪及BP神经网络的大坝变形分析[J].人民长江,2011,42(9):90-93.
[6]王润英,伍彦熹,慕子煜,等.基于M估计的抗差Kalman滤波算法在某混凝土重力坝变形监测中的应用[J].水电能源科学,2015,33(12):89-92.
[7]HAWKINS D M.Identification of outliers[M].London:Chapman and Hall,1980.
[8]邹晓磊,薛桂玉.大坝监测数据异常值识别方法探讨[J].水电能源科学,2009,27(5):83-85.
[9]王奉伟,周世健,罗亦泳.自适应LMD融合新小波阈值函数的信号去噪[J].人民长江,2016,47(13):97-101.
[10]李士心,刘鲁源,杨晔,等.基于平稳小波变换的陀螺仪信号去噪方法[J].天津大学学报,2003(2):165-168.
[11]ZHONG S,OYADIJI S O.Crack detection in simply supported beams using stationary wavelet transform of modal data[J].Structural Control and Health Monitoring,2011,18(2):169-190.
[12]BIRG L,MASSART P.From model selection to adaptive estimation[A].In:Pollard D,Torgersen E,Yang G L.Festschrift for Lucien Le Cam:Research Papers in Probability and Statistics[M].New York:Springer,1997.
[13]秦毅,王騰,何启源,等.高密度小波变换在滚动轴承复合故障诊断中的应用[J].重庆大学学报,2013(3):17-23.
[14]叶建雄,李志刚,WU J,等.基于SVR模型的水下焊接最佳工艺[J].焊接学报,2017,38(12):69-72.
[15]XIANG J,LIANG M,HE Y.Experimental investigation of frequency-based multi-damage detection for beams using support vector regression[J].Engineering Fracture Mechanics,2014,131:257-268.
(编辑:郑 毅)
Abstract:Deformation is the most direct reflection of gravity dams safety,and the operating behavior of a gravity dam can be accurately monitored and forewarned by reasonable deformation prediction models.The gross error of the original deformation signal is eliminated by the Hampel filter.The multi-scale component of the deformation signal was obtained by stationary wavelet decomposition,and the denoising effect of different threshold functions and threshold determination methods were compared and analyzed.For the preprocessed and original data,the deformation prediction models were established by stepwise regression analysis,BP neural network,and support vector regression respectively,and the prediction effect of each model was compared and analyzed.The results showed that the SVR model had the best prediction results,and the prediction accuracy of the preprocessed data was better than that of the original data.
Key words:gravity dams;deformation prediction;stationary wavelet decomposition;threshold denoising;support vector regression

