基于套合模型的土壤有机质空间尺度效应分析

陈弘扬 邹宏光 方兵 周鹏飞 庄红娟 宋强 杨斌 张世文

摘要：为了探索土壤有机质含量在空间分布上的特征，更好地服务于土地生产力和土壤肥力评价，以北京市平谷区西北部桃园为研究对象，通过地统计学方法分析了土壤有机质空间尺度效应。结果表明，指数模型对土壤有机质含量拟合效果最佳，各尺度上的样点数据均符合正态分布，其空间结构对空间尺度的依赖性较明显;理论半方差变异函数I值和（Z*-Z）2检验表明，L尺度下普通克里格法预测效果比套合模型法好，在M、S尺度下结果刚好相反;土壤有机质含量在空间分布上呈集中连片的趋势，有机质含量低值主要集中在研究区的西南部和中东部区域，有机质高值主要分布在北部和南部的少部分区域。因此，在采样密度较大的尺度下基于多尺度套合法针对土壤有机质空间变异进行研究，使得插值结果达到更高的可靠性，可为制定土壤肥力评价方案提供科学的指导。

关键词：土壤有机质;尺度效应;空间变异;套合模型

中图分类号：S153.6+21   文献标志码： A

文章编号：1002-1302（2021）21-0247-06

收稿日期：2021-02-24

基金项目：国家重点研发计划（编号：2016YFD030080104）。

作者简介：陈弘扬（1996—），男，安徽合肥人，硕士研究生，主要从事土壤肥力相关研究。E-mail：136960529@qq.com。

通信作者：张世文，博士，教授，博士生导师，主要从事土壤过程定量化相关研究。E-mail：mamin1190@126.com。

土壤是地表上体系最庞杂，功能最多样的生态系统之一;土壤有机质是以多种形式和状态存在于土壤中的含碳有机化合物，是土壤系统的不可或缺的关键成分[1]。明确土壤有机质含量的动态变化，采用合适的方法掌握其空间分布规律，是土地生产力和土壤肥力评价的关键[2]。

目前，应用地统计学方法来研究土壤关键指标空间变异特征是土壤特性研究的热点[3]。学者对土壤关键指标的空间结构开展大量研究，如利用普通克里格法分析了新疆伊犁地区[4]、兰州市某典型生态区[5]、山东半岛东部地区[6]、意大利农牧交错带[7]内土壤属性的空间分布特征，但有学者指出普通克里格法对土壤有机质含量的插值效果并不是很好[8]。与此同时，有研究指出所选择的空间尺度是目前多数涉及有机质空间变异研究的前提[9-10]，少有研究专门论述同一研究区域、不同空间尺度上的土壤特征变异规律。部分研究探讨了不同空间尺度的土壤特征变异特征，并对尺度效应进行了验证[11-12]，但是缺乏更加深入研究，有必要对土壤有机质含量处于连续空间的变异特征进行更多的研究，使土壤空间管理达到更高的要求。

本研究重点对各个尺度下的土壤有机质空间变异结构特征进行了分析，在研究过程中提出多尺度套合模型，并将其应用到了黄淮海平原典型农业区的研究中，以期有效地揭示果园中有机质含量的空间分布特征，为土地生产力和土壤肥力评价提供科学依据。

1 材料与方法

1.1 研究区概况

研究区位于北京市平谷区，占地面积为 3 004.94 hm2，其中果园面积为2 764.39 hm2。研究区属温带大陆性季风气候，东北地势较高，西南较低，土地利用类型以果园为主，是全国重要大桃产地之一。土壤质地以轻壤质为主，土壤母质以钙质岩类风化物为主;土壤亚类以普通褐土为主，还包括淋溶褐土、碳酸盐褐土、;地面高程为34.55～992.77 m 。为了揭示区域土壤有机质含量空间分布特征的尺度效应，本研究以不同采样密度来反映采样尺度的变化，研究不同采样密度下有机质的空间变异特征。

1.2 样品采集和处理

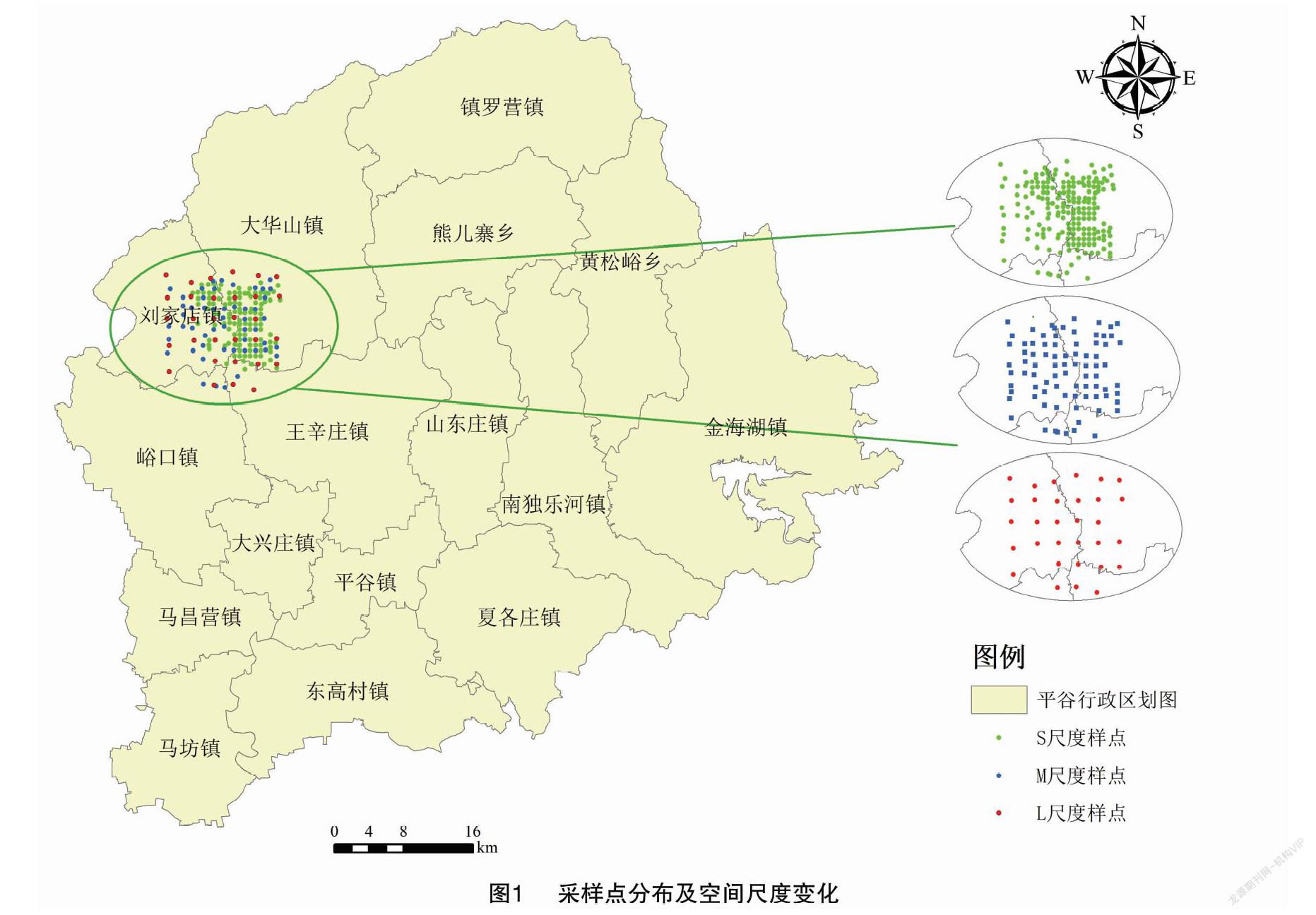
于2019年9月进行土壤样品采集，利用ArcGIS 10.1软件对研究区实行网格嵌套加密布点，布点过程分为如下3个步骤：首先，按照网格布点的方式，叠加研究区果园图斑，通过筛选在研究区布设31个采样点;然后，在果园分布较密集的区域加密布设51个采样点;最后，在前2次布点的基础上再次加密布设111个采样点，共布设了193个采样点（图1）。根据采样图和地块的坐标位置确定取样地块，到达事先布设的点位附近，选择代表性区域，采集表层土样，避开特殊地形部位以及堆过肥料的地方取样。如果选择位置无法达到，选择距离该样点较近且离公路较远的典型农田地块。采样时使用GPS进行精确定位，根据取样地块的大小和形状采用“S”法，随机采取5个样点的混合样，取样深度为 0～20 cm，取样质量为2 kg左右。采用重铬酸钾容量法测定每个土壤樣品的有机质含量。

1.3 尺度的定义与划分

尺度一般指的是时间或者空间的幅度[13]。本研究将重点分析空间尺度的异质性。由于非网格布点，研究过程中为了对空间尺度变化进行分析，采用了采样密度的间接描述方法，各个尺度的采样密度不同，可以对有机质的空间分布变异规律进行研究。总样点数是193个，其中L尺度上的采样密度较小，为0.011个/hm2，样点数为31个;M尺度上的采样密度居中，为0.03个/hm2，样点数为82个）;S尺度上的采样密度最大，为0.071个/hm2，样点数为193个（M、L尺度样点包含在S尺度内，图1）。

1.4 研究方法

1.4.1 变异函数的理论模型 为了研究不同采样密度下土壤有机质的空间变化规律，采用变异函数对土壤有机质含量进行研究，该函数已经广泛应用于地统计分析中[14]，以此对空间内区域变量Z（x）的相关性进行描述：

γ*（h）=12N（h）∑N（h）i=1[Z（xi）-Z（xi+h）]2。（1）

式中：γ*（h）表示对应的半方差;Z（xi+h）、Z（xi）分别代表点xi+h、xi位置的指标实测数据;h代表两点的空间分隔距离（m）;N（h） 代表间隔距离为h的样本点对数。

1.4.2 空间变异的多尺度套合模型及模型检验 目前在土壤属性空间变异结构分析中多采用半变异函数，但多尺度区域的区域化变量变化复杂，须要采用多个模型来对其空间变异性进行分析，即多结构的叠加[15]，也就是套合结构，公式如下：

γ*（h）=γ*0（h）+γ*1（h）+γ*2（h）+…+γ*n（h）=∑ni=0γ*i（h）。（2）

式中：γ*i（h）代表理论模型，即各个尺度下的空间结构特征;γ*0（h）代表套合结构的块金方差。

本研究选择了GS+软件确定不同尺度下的变异函数最佳理论模型，采用I值作为综合指标进行理论模型的最优值检验[16]。

I=（Z*-Z）2×P×1-1[（Z*-Z）/S*]2+（1-P）;（3）

P=0.1    0≤（Z*-Z）2<1000.2    100≤（Z*-Z）2。（4）

式中：Z代表实测数据，Z*、S*分别代表某个实测位置的克里格估计以及对应的标准差。根据I值大小可以判断模型的应用效果，I值越大，则对变量结构的代表性越差。

1.4.3 数据处理和分析方法 显著性分析以及描述性统计分析等运用SPSS 21.0完成;基于ArcGIS 10.1中地统计分析，进行多尺度空间结构套合和空间插值;半方差函数的计算采用GS+软件完成;图形绘制工作在Origin软件完成。

2 结果与分析

2.1 土壤有机质描述性统计

地统计学中，数据的非正态分布会使半变异函数形成一定的比例效应，导致基态值、块金值增大，使得部分结构特征隐藏，最终降低估值的精度[17]。如表1所示，L、M、S尺度下的土壤有机质含量均符合正态分布，所以3种尺度均可进行有机质多尺度空间结构分析。

研究区不同尺度下土壤有机质含量统计特征具有一定的可比性，3种尺度上有机质含量均值为21.42～21.60 g/kg，差异不大，由此可知研究区的土壤有机质含量分布比较均匀。土壤有机质含量标准差与采样密度直接相关，二者存在负相关关系，相对于L尺度，M、S尺度的土壤有机质含量表现出更高的集中性。当变异系数（CV）>1时，认为指标属于强变异;当CV<0.1时，认为指标属于弱变异;当CV介于0.1到1之间时，认为指标属于中等变异[18]。由表1可知，3种尺度均属于中等程度变异，其变异系数在16.05%～17.74%之间。

对于土壤有机质含量的描述性统计只能说明其含量变化，而对于土壤有机质独立性、结构性等特性的描述，须要基于地统计学法进行进一步分析和探究[19]。

2.2 不同尺度下土壤有机质空间变异分析

如表2所示，各尺度下的土壤有机质含量的最优理论模型均为指数模型。基底效应反映了土壤有机质空间变异的空间相关程度。基于区域化变量空间的相关性分级标准，在变量基底效应分别处于﹥75%、25%～75%、<25%的范围时，分别说明空间相关性较弱、中等、较强[20]。各尺度上土壤有机质空间相关性等级为中等，变异系数在46.30%～52.40%之间，表明结构性因素（高程、土类等）和随机因素（人类活动等）的差距不显著。在研究中发现，随着采样密度的增加，L、M、S尺度中的块金值逐步降低，由此可以证明，在采样密度变大的过程中，各个尺度都存在一定的空间变异性，结构性特征不同;L、M、S尺度的土壤有机质含量的块基比[C0/（C0+C）]随着采样密度的增加，持续降低，即表明在采样密度增大的过程中，增大了样点的空间相关性，表现出一定的正相关性。此外，L、M、S尺度上土壤有机质各理論半变异函数参数值均相差较大，尤其块金值（C0）和块基比[C0/（C0+C）]相差较大，表明随着研究尺度的增大，在L、M尺度上不能表现出差异的背景因素在S尺度上发挥着较大的作用，所以在研究M、S尺度的空间变异特征时如果选择L尺度，则难以保证结果的可靠性。结合上述分析可知，在研究土壤有机质的变异特征时须要采用各个尺度的套合模型，由此才能保证与实际结果的一致性。

2.3 多尺度套合模型拟合

结合尺度套合理论，块金值主要是S尺度下无法描述的空间变异，各个尺度都符合指数模型，由此得到的多尺度套合模型如下所示：

γ（h）=5.27×Nugget+6.11×Expomemtial（1480）+6.47×Expomemtial（1970）+6.64×Expomemtial（2520）。（5）

式中：Nugget表示块金值;Exponential表示指数模型。

土壤有机质含量的半方差函数经套合模型拟合后，对各尺度样点数据进行空间插值，称为套合模型空间插值。本研究比较了套合模型法插值和普通克里格法插值精度，并针对半方差函数进行了最优性检验，主要采用是十字交叉检验法，基于（Z*-Z）2进行计算分析。由表3可以看出，在L、S尺度下套合模型的I值和（Z*-Z）2都大于普通克里格法，在M尺度下普通克里格法的I值大于套合模型法，说明不同尺度下普通克里格法和套合模型法的预测效果各有优缺点，且随着采样密度的不断增大，2种方法的预测精度均在逐渐的增高，套合模型的预测精度与普通克里格法较为接近。

2.4 实测值与普通克里格法、套合模型法插值的对比分析

由表4可以看出，3种尺度下的土壤有机质含量平均值预测结果与实际结果基本相差0～0.1 g/kg，但是变异系数、最大值以及方差均低于实际数据，而最小值相对于实际结果更高。由此可以证明，2种方法对于原始数据起到了“压缩”的效果，其中克里格插值法能够有效地降低数据的变异性[21]。相对于普通克里格法，L尺度下的套合模型法插值结果在变异系数、标准差以及数据范围更小，即证明该方法的“压缩”效果更明显，这样会使预测效果变差;M、S尺度的插值效果与L尺度刚好相反，“压缩”效果较小，表明套合模型法插值比普通克里格法效果要好，更能反映实测值的大小。

根据表5可知，相对于普通克里格法，套合模型法在L尺度的土壤有机质含量平均绝对误差、平均相对误差更高，而相对误差≤20%的样点百分数低于普通克里格法;在M、S尺度下土壤有机质含量平均绝对误差和平均相对误差都表现为套合模型法小于普通克里格法，而相对误差≤20%的样点百分数高于普通克里格法。因此，这也验证了在M、S尺度下套合模型插值后预测值与实测值吻合度高于普通克里格法，插值效果优于普通克里格法，而L尺度下的插值效果则是普通克里格法较好。

2.5 土壤有机质含量的空间分布分析

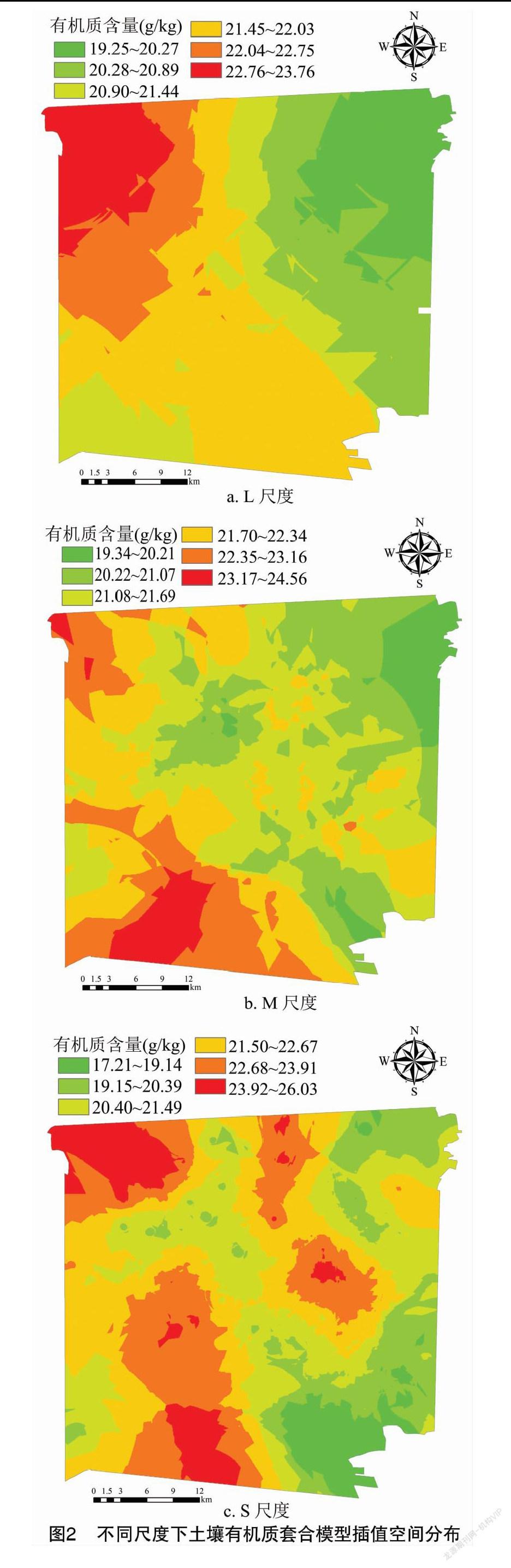
由图2可以看出，土壤有机质在空间分布上呈现集中连片的趋势，有机质含量低值主要集中在研究区的西南部和中东部区域，有机质高值主要分布在北部和南部的少部分区域。在空间结构性方面，L、S尺度下样点布置均匀，有机质在向各方向上扩散较均匀，空间分布有团块状趋势，等值线平滑;而在M尺度上由于布点的不均匀性和边界的无样点性，会对数据产生“压缩”作用，从而使研究区的北部和东部少部分区域在空间上呈现出条带状分布。

形成有机质空间分布的主要原因是以错河为界限将研究区分为两部分，在错河两岸的高海拔处由于汛期降雨较大，受暴雨冲刷影响，从而使有机质流失严重，在错河的下游有机质随水流的集聚作用，使下游的有机质含量普遍高于上游区域;从施肥角度看，研究区的主要经济作物为桃树，桃树在生长的过程中对肥料的需求较大，从而使研究区的有机质含量普遍高于平谷区平均水平，并且在研究区有机质高值区域，桃树的年龄以10年左右，这种年龄桃树相对于其他年龄桃树对养分的需求更大，从而使有机肥的投入量普遍高于其他地区，长期以往，最终导致这些区域有机质含量普遍高于其他地区。

3 结论

土壤有机质的空间结构性与空间尺度变化直接相关，一般大尺度无法对小尺度中的结构性进行呈现。正是由于各个空间尺度下的土壤有机质空间结构不同，需要通过多尺度套合模型来进行空间分布特征的分析，由此才能得到较为准确的结果。

基于最优性I值检验以及（Z*-Z）2值可知，相对于普通克里格法，处于L、S尺度下的套合模型I值以及（Z*-Z）2均明显更高，而M尺度的普通克里格法的I值大于套合模型法，说明不同尺度下普通克里格法和套合模型法的预测效果各有优缺点。此外通过绝对误差以及相对误差均值、差异显著性检验的结果可知，相对于普通克里格法，处于M、S尺度下的套合模型插值之后的预测结果与实际结果保持了更高的一致性，但是L尺度的插值效果则完全相反。

土壤有机质在空间分布上呈现集中连片的趋势，有机质含量低值主要集中在研究区的西南部和中东部区域，有机质高值主要分布在北部和南部的少部分区域。M尺度下研究区部分地区土壤有机质空间上呈现部分条带状分布的主要原因是由于M尺度下样点布设不均匀性和边界的无样点性，对数据产生压缩作用，使其插值效果较差。

参考文献：

[1]王 爽，王 鹏，李少娟，等. 大型城市会展地土壤养分空间分布特征研究——以2019北京世界园艺博览会为例[J]. 中国农业大学学报，2017，22（1）：129-138.

[2]赵业婷，常庆瑞，李志鹏，等. 渭北台塬区耕地土壤有机质与全氮空间特征[J]. 农业机械学报，2014，45（8）：140-148.

[3]王国芳，张吴平，毕如田，等. 县域尺度农田深层土壤有机质的估算及空间变异特征[J]. 农业工程学报，2019，35（22）：122-131.

[4]许尔琪，张红旗.伊犁新垦区土壤有机质的克里金插值和条件模拟多尺度分析[J]. 土壤，2013，45（1）：91-98.

[5]王 潇，赵建华，董 博.基于克里格插值的兰州市土壤全氮和有机质空间变异研究[J]. 甘肃农业科技，2011（4）：5-7.

[6]张文龙，李玉环，姬 祥.基于地统计学的耕层土壤有机质空间变异及不同插值模型的比较[J]. 中国农学通报，2011，27（6）：256-260.

[7]Cicchella D，Giaccio L，Dinelli E，et al. GEMAS：Spatial distribution of chemical elements in agricultural and grazing land soil of Italy[J]. Journal of Geochemical Exploration，2015，154：129-142.

[8]谢恩泽，赵永存，陆访仪，等. 不同方法预测苏南农田土壤有机质空间分布对比研究[J]. 土壤学报，2018，55（5）：1051-1061.

[9]朱洪芬，南 锋，徐占军，等. 黄土高原盆地土壤有机质与影响因子的空间多尺度关系[J]. 生态学报，2017，37（24）：8348-8360.

[10]Foroughifar H，Jafarzadeh A A，Torabi H，et al. Using geostatistics and geographic information system techniques to characterize spatial variability of soil properties，including micronutrients[J]. Communications in Soil Science & Plant Analysis，2013，44（8）：1273-1281.

[11]于 婧，周 勇，聂 艳，等. 江汉平原耕地土壤氮素空间尺度套合与变异规律研究[J]. 中国农业科学，2007，40（6）：1297-1302.

[12]Wu Z H，Liu Y F，Chen Y Y，et al. Spatial interpolation model of soil organic carbon density considering land-use and spatial heterogeneity[J]. Chinese Journal of Applied Ecology，2018，29（1）：238-246.

[13]霍霄妮，李 红，张微微，等. 北京耕作土壤重金属多尺度空间结构[J]. 农业工程学报，2009，25（3）：223-229.

[14]于 洋，卫 伟，陈利顶，等. 黄土高原年均降水量空间插值及其方法比较[J]. 应用生态学报，2015，26（4）：999-1006.

[15]杨 勇，李卫东，贺立源.土壤属性空间预测中变异函数套合模型的表达与参数估计[J]. 农业工程学报，2011，27（6）：85-89.

[16]刘国顺，常 栋，叶协锋，等. 基于GIS的缓坡烟田土壤养分空间变异研究[J]. 生态学报，2013，33（8）：2586-2595.

[17]高 歆.基于线性GSI二维半变异函数各向异性结构建模及估计研究——以DEM数据为例[J]. 地理研究，2020，39（11）：2607-2625.

[18]葛 畅，刘慧琳，聂超甲，等. 土壤肥力及其影响因素的尺度效应——以北京市平谷区为例[J]. 资源科学，2019，41（4）：753-765.

[19]杨子清，陈平留，刘 健，等. 基于Kriging法的森林土壤养分空间插值[J]. 福建农林大学学报（自然科学版），2012，41（3）：296-300.

[20]刘 聪，周 清，屈金莲，等. 不同地形条件下样点密度对土壤养分空间变异的影响[J]. 湖南农业大学学报（自然科学版），2013，39（1）：80-85.

[21]煙贯发，杜百利，张冬有，等. 松花江哈尔滨段悬浮物含量遥感反演与克里格插值预测精度对比[J]. 湿地科学，2015，13（2）：184-189.