基于SOAM方法的武汉疫情期间空气质量评价研究

摘 要： 本文以武漢市的COVID-19疫情主要发生期为案例，研究在疫情影响下，经济处于一种基本停滞或下滑的特殊状况下空气质量如何变化。根据相关网站提供的空气质量日报数据，对该市主要疫情期的2020年1-4月和正常年份的2019年同期，按本文提出的SOAM（Space Optimal Aggregation Model）方法进行了各月的综合评价。结果表明，2020年空气质量呈现出逐步向好的趋势，且2020年1-4月份空气质量皆优于上一年的2019年同期。这说明武汉市受疫情影响被迫采取的停工、停产和封城措施而导致的经济停滞或下滑现实，在客观上使得该市的空气质量在一定程度上得到了好转。此外，还应用本文提出的经济影响度模型对各主要空气污染物进行了经济影响度的计算。结果表明，经济因素对主要空气污染物PM2.5、SO2、NO2各自的影响程度分别为19%、12%和49%。这说明在经济因素的作用下，各空气污染物都会受到不同程度的影响。而在排除经济因素影响外，其他非经济因素，如城市的地理位置、气候等自然因素以及其他省份和地区的输入性污染等也会对一个城市的空气质量产生一定的影响。因此，在适度经济发展的情况下，促进各地区产业结构的转型、改进北方冬季燃煤取暖的传统方式，全国各地区的联防联控以及环境生态建设才是解决空气污染的有效途径。

关键词： 武汉市;COVID-19;指标信息空间最优集结;经济;空气质量评价

中图分类号： X 82

文献标志码： A

Study on Air Quality Evaluation During Epidemic Period inWuhan Based on SOAM Method

LI Lei

（School of Business， Jiangnan University，Wuxi 214122， China）

Abstract： A novel economic impact model is proposed by this paper to analyze the impact of economic downturn on the air quality in Wuhan during the epidemic period， and to explore the effective solutions to improve the urban air pollution. The Space Optimal Aggregation Model （SOAM） is used to evaluate the air quality of Wuhan from January to April in 2019 and 2020. The analysis results show that the air quality of Wuhan from January to April 2020 is better than that of the same period in 2019， and it shows a gradually better trend. This shows that although the measures of household isolation， shutdown and production stoppage adopted during the epidemic period in Wuhan caused economic downturn， it objectively improved the air quality of the city. In addition， the economic impact degree of the main air pollutants are calculated by the SOAM. The results showed that the economic factors affected the main air pollutants PM2.5， SO2 and NO2 by 19%， 12% and 49% respectively. This shows that under the influence of economic factors， all air pollutants will be affected to varying degrees. In addition to economic factors， other noneconomic factor will also have a certain impact on the air quality of a city. Therefore， under the condition of moderate economic development， the effective way to solve urban air pollution is to promote the transformation of industrial structure in various regions， improve the traditional way of coal-fired heating in winter in northern China， and the joint prevention and control of all regions in the country and the construction of environmental ecology.

Key words： Wuhan city; COVID-19; the optimal aggregation of index information space; economic; air quality evaluation

过去相关领域研究者往往研究的重点聚焦在经济增长对于空气质量影响上面。而对于经济变量几乎为零或经济负增长情况下，由于缺少现实中适合的案例，而没有研究的机会。本文是以COVID-19病毒在中国最初爆发地的武汉市为研究背景，探讨该市由于受到疫情影响被迫采取的停工、停产和封城措施而导致的经济停滞或下滑现实对其空气质量的影响。而这次武汉案例却恰好给研究者提供了一次难得的、却真实的在经济变量近似为零情况下，考察对空气质量影响的特殊实验。在研究方法上，本文提出了一个空间最优集结模型（SOAM）的空气质量评价方法。利用该方法，通过对武汉市2020年1～4月份与正常年份的上一年同期比较研究，以分别评估受疫情影响，经济变量近似为零以及正常年份经济变量大于零时空气综合质量状况，以期考察经济因素对于城市空气质量的影响。此外，本文还试图给出各经济因素对主要污染物的影响度模型，并估计出单纯经济因素对于每一种污染物的影响程度，以确定单纯经济因素对于空气污染物的影响比重。从而，间接的估计除了经济因素外，城市空气污染的其他影响因素，如，地理位置、气候等自然因素以及其他省份和地区的输入性污染等影响的可能。给城市常态下如何适度调整经济发展速度和总量，促进各地区产业结构的转型、改进冬季燃煤取暖的传统方式以及全国各地区的联防联控以及环境生态建设，提供有价值的参考依据。

1 文献综述

上个世纪60年代美国学者Boulding曾形象的将地球比拟成为太空中的一艘宇宙飞船。他认为人口和经济的无序增长迟早会使船内有限的资源耗尽，而生产和消费过程中排出的废料将使飞船污染，毒害船内的乘客，此时飞船会坠落，社会随之崩溃。然而，几十年过去了，当今世界环境问题并没有得到根本性的好转。进入到工业后期和发达阶段，随着人口的密度增加和经济的高速发展，包括中国在内的许多国家空气污染加剧，引起了科学界的广泛关注。2008年汇集了四大洲35个国家的200多名科学家参加了空气质量管理国际研讨会。会上就城市和区域范围内的空气质量评价、实践与评价标准的选择进行了广泛的探讨，其影响意义深远。

探讨经济增长与空气质量之间的关系研究，一直是环境经济领域里的热点问题之一。近些年来的研究成果越来越多的体现在了深刻揭示各种经济、空气污染物因素变量之间的定量关系上面。Kukla-Gryz通过经济活动结构和空气污染强度两个因素建立的结构方程模型，揭示了经济活动结构的变化导致了发展中国家空气污染的增加。Aristotelous根据1961年至2010年不同国家组的非平衡面板数据集，研究了经济增长和空气污染之间的关系。结果表明，经济增长和空气污染之间的关系取决于一个国家的经济发展水平。Ouyang等采用面板阈值模型，研究了30个经合组织国家的环境调控和经济增长对PM2.5的非线性影响，并探讨了PM2.5排放的主要驱动社会经济因素。分析结果表明，随着环境政策力度的加大，PM2.5排放先上升后无显著相关性，如果目前的趋势继续下去，排放有望减少。Soukiazis等根据一组28个经合组织国家的有力证据考察了2004—2015年可再生能源、经济发展与污染的关系，使用联立方程系统方法，描述经济变量之间的相互关系以及可再生能源和污染排放与反馈效应。Urhie等采用了适度中介模型，并利用Hayes开发的分析工具PROCESS macro解释了经济增长、空气污染和健康表现之间的相互作用。Sarkodie利用新的Breitung-Candelon Spectral Granger-causality关系来解释因果关系的趋势，验证了物质消耗与经济增长之间的反馈假设。研究表明，金属矿石的消耗可以预测经济增长、收入水平和可再生能源的消耗，但它会造成环境空气污染。

自1955年Environmental Kuznets Curve（EKC）假设提出以来，一些经济学家期望世界上经济高速发展的国家或地区在经济发展到一定程度，环境质量能够出现EKC假设预计的那样，出现好转的拐点。然而现实中的一些研究验证表明，很多案例不支持EKC假设成立。Cin曾对1997—2009年19个亚洲国家的环境库兹涅茨假说进行了实证研究。结果表明，人均GDP与CO2排放量之间存在正相关关系。在以出口为导向的亚洲国家中，没有关于环境库兹涅茨假说的有力证据。Georgiev和Mihaylov利用30个经合组织国家的面板数据，对四种本地（SOx、NOx、CO、VOC）和两种全球（CO2、GHG）空气污染物的环境库兹涅茨曲线（EKC）假设进行了检验。假设的收入和污染之间的倒u型关系并不适用于所有的气体。Tsujimoto以Environmental Kuznets Curve（EKC）假设为基础，根据1980年到2014年跨越7个州的35年时间序列的数据，运用回归分析方法，探讨波斯湾国家的经济增长（人均GDP）与空气污染（人均CO2排放）之间的关系。研究结果表明，EKC假设的支持力度不够显著。

近些年，由于中国经济高速发展带来了诸多的空气污染问题，引起了学术界的高度关注。许多研究者以中国的经济增长与空气污染作为研究背景，试图发现经济增长与空气污染间存在的潜在规律。Yang等研究了中国经济增长与环境污染和能源消耗的关系，结果表明：中国经济增长与环境污染和能源消耗存在长期稳定的协整关系，而且经济增长与能源消耗之间存在着长期双向因果关系，能源消耗是环境污染强单向因果关系。Xie等根据中国高分辨率人口密度地图、卫星检索的PM2.5浓度和省级卫生数据，考察了前10年经济发展与雾霾和雾霾事件间的关系，在一些人口密度高的内陆发展中省份（如河南、安徽、四川），由于更多的污染和资源密集型产业转移到这些地区，使得这些地区的雾霾污染呈上升趋势。Lu 等利用中国30个省份2002年至2014年的面板数据，采用联立方程模型（SEM），描述了经济发展、环境质量和公共卫生之间关系的三个方程组成，验证了经济发展对于环境的负面影响。Qiu 等发放了一份包含29个问题的匿名问卷，使用统计卡方检验来确定支持经济放缓政策或要求政府采取更多措施抗击雾霾污染的人口统计学受访者群体。结果表明，年龄在31岁到50歲之间的人，以及那些生活在高污染地区的人，支持经济放缓政策。Qiu 等为研究识别社会经济发展对PM2.5变化的潜在影响，采用空间回归和地理探测器技术，利用2014年中国190个城市945个监测站的数据，评估了社会经济因素与PM2.5浓度之间的关联方向和强度。Shi 等以中国31个省份为研究对象，采用对数均值分解指数法将解耦弹性系数分解为尺度解耦弹性、技术解耦弹性和结构解耦弹性，分析了2001—2015年经济增长与环境污染的解耦关系。Zhu 等利用2013—2017年中国73个重点城市的面板数据，采用VECM、脉冲响应函数、方差分解等方法进行实证估计。结果表明，PM2.5与经济增长等因素变量之间存在双向因果关系。Xie 等根据2015年中国249个城市的大样本，利用半参数空间自回归模型研究了经济增长对PM2.5污染的影响。Yang 等研究选取了雾霾严重的内陆地区成都平原经济区（CPEZ），利用空间计量经济学方法，识别了2006 —2016年期间PM2.5浓度的时空分布特征及其背后的社会经济因素。根据空间德宾模型（spatial Durbin model， SDM）的结果表明，人口密度、单位产出能耗、国内生产总值（GDP）、人均GDP等社会经济因素对PM2.5浓度有正向影响。

综上文献发现，其研究成果没有涉及到如何将不同时间节点上的多指标空气质量数据在某一段时间内进行集结，从而评价出这一时间段内的总体空气质量以及与当时经济状况的关系。因此，本文提出了一种基于SOAM的方法，以武汉市的COVID-19疫情主要发生期为案例，根据该市2020年主要疫情期的1-4月的日报数据，进行数据信息的集结，并与正常年份的2019年同期相比，得出在经济下滑或停滞期该市空气质量的变化以及对主要空气污染物PM2.5、SO2、NO2各自的影响程度。以期得出经济因素与空气质量之间的内在规律，为城市的经济发展与生态环境协调发展，提供参考依据。

2 理论基础

若要评估一个城市在某一时间段的空气质量状况，则必须首先要将该时间段内的每个时间节点上的多指标数据进行集结，以便得到该时间段的多指标数据的集结值。而传统的集结方法是Yager 等人提出的有序加权平均（OWA）算子和诱导的有序加权平均（IOWA）算子。但，无论是OWA法还是IOWA都不是最优集结方法，都存在着集结精度较低的问题。因此，不能够真实的反映出集结点的代表性。本文受到Steiner-Weber点问题的启发，拟建立以Steiner-Weber点问题为原型的Space Optimal Aggregation Model（SOAM）。

2.1 模型构建

首先考虑平面Steiner-Weber点问题。该问题是在Fermat-Torricelli点问题基础上给出的。1643年法国数学家Fermat首次提出的Fermat点问题。Fermat点问题是指如何找到距任意一个平面三角形三个顶点距离之和最小的点。因Torricelli采用初等几何方法最先解决了该问题，故该点常被称为Fermat-Torricelli点。其后，Steiner和Weber对于Fermat-Torricelli点进行了实质性的拓展，拓展后的点也被称为Steiner-Weber点。所谓Steiner-Weber点，是在平面上给定了m个已知点（m 个已知点可以超过 3个），满足到这m个已知点加权距离之和最短的点。其数学模型为：

minx f（x）=min ∑mi=1αi‖x-ai‖（1）

其中，向量：a1，a2，Λ，am∈Rn;m≥3;αi为距离权重，∑mi=1αi=1，αi>0;‖·‖欧几里得向量范数。

通过求解模型（1）得到的最优解，即可认为是最优集结点坐标。

然而，如果要求解多指标的空间最优集结问题，显然就不能够再采用平面Steiner-Weber点模型了。平面Steiner-Weber点模型需要拓展为空间Steiner-Weber点模型。为此，本文提出了一个Space Optimal Aggregation Model（SOAM）。

设欧式空间Rn上的m个已知点的点集为：

{Ai|（xi1，xi2，Λ，xin），i=1，2，Λ，m}（2）

如果存在一点：B*（x*1，x*2，…，x*n）满足

min αi|AiB*|=min ∑mi=1αi∑nj=1（x*j-xij）212（3）

式中，αi为距离权重，∑mi=1αi=1，αi>0，则称B*为m个已知空间点的Steiner-Weber点，即最优集结点。

为了直观起见，仅以n=3（三维属性构成的空间坐标系），B*维空间的最优集结点，即三维空间的Steiner-Weber点，见图1。

根据上述建立的空间Steiner-Weber点模型，本文来探讨空气质量监测指标最优集结问题。对于q个月，每个月中包含m天的n个空气质量监测指标数据，可以用下面的矩阵来表达：

A1=x111x112…x11n

x121x122…x12n

MM…M

x1m1x1m2…x1mn

A2=x211x212…x21n

x221x222…x22n

MM…M

x2m1x2m2…x2mn

Aqxq11xq12…xq1n

xq21xq22…xq2n

MM…M

xqm1xqm2…xqmn

其中，xkij為第k个月份（k=1，2，…，q）中第i天（i=1，2，…，m）在第j个空气质量监测指标数据（j=1，2，…，n）。将矩阵A1，A2，…，Aq映射到q个n维欧式空间上：En1，En2，…，Enq。

根据上述映射关系可以构建与其相对应的q个n维欧式空间坐标系，并由空气质量监测指标数据构成的空间点集，建立起基于空间Steiner-Weber点的空气质量监测指标数据的集结模型。

设Pki=（xki1，xki1，…，xkin）i=1，2，…，m;k=1，2，…，q为第k个月中第i天的空间点，则（Pk1，Pk2，…，Pkm）为第k个月的点集。当满足：

dk=min ∑mi=1αi‖PkiP*k‖ =min ∑mi=1αi∑ni=1（xkij-x*kj）212（4）

式中，P*k为第k个月最优集结点（k=1，2，…，q）;αi为第i天坐标点到第k个月最优集结点P*k的距离权重。

令P*=（P*1，P*2，…，P*q）为q个月的最优集结点集。通过求解式（4），可以得到最优集结矩阵：

R*=x*11x*12…x*1n

x*21x*22…x*2n

MM…M

x*q1x*q2…x*qn（5）

2.2 求解模型的算法

求解（4）式，相当于在q个n维欧式空间中，求解满足到m个已知点欧式距离之和最短的点集P*。当n=2，m=3时相当于求解平面Fermat-Torricelli点问题，采用初等几何方法即可求解。当n=2时，m>3相当于求解平面Steiner-Weber点问题，通常应用重心法和微分偏导法来求解。当n>2时，m>3，拓展为求解空间点的问题。目前，相关研究领域的文献中，鲜有介绍求解该问题的算法。本文拟采用一种以模拟自然界植物向光性生长的仿生算法——The plant growth simulation algorithm （PGSA）进行求解。

PGSA算法是本文作者之一李彤于2005年提出的一种以植物向光性机理为启发式准则的智能优化算法。该算法是将优化问题的解空间当作植物的生长环境，将最优解当作光源，根据真实植物的向光性特征，建立枝叶在不同光线强度环境下向着阳光快速生长的演绎方式。自PGSA创立后，已引起国内外众多学者的高度关注，并将其应用于各自的研究领域。与其他智能算法相比，均取得更优的结果。

利用PGSA，求解欧式空间最优集结点的步骤如下：

Step 1 确定初始生长点am∈X，X为Rn中的有界闭箱，这些初始生长点am为有界闭箱内随机均匀的点;

Step 2 求解各生长点的生长概率：

pm=∑ni=1（1/|amSi|）∑vm=1∑ni=1（1/|amSi|）（m=1，2，….v）（6）

Step 3 根据Step 2的结果建立各生长点在闭区间上内的概率空间，以随机数来选择本次迭代生长点;

Step 4 确定步长λ（一般取l/1000），生长点am按照α=90°的L系统进行生长，用新的生长点中集结点替代am;

Step 5 如若不再产生新的生长点且达到预设的迭代次数，分别得到全局最优解和局部最优解，则停止计算，否则转步骤2。

PGSA算法的程序框图，见图2。

2.3 属性权重及方案评价

为了确定各空气质量指标的属性权重及方案评价，本文采用各项属性指标自身所包含信息的客观赋权法——特征根法（Characteristic root method）来确定指标属性的权重。

对于具有m个样本 ，每个样本有n个指标的空气质量检测数据，构成m×n阶矩阵r，通过r求出其相关系数矩阵，并求出n个特征根λj，从而给出各指标属性权重wj：

wj=λj/∑nj=1λj（6）

采用线性加权法来进行方案的评价：

φ（A）=W·（R*）T（7）

式中，A=（A1，A2，…，Aq）;W=（w1，w2，…，wn）;R*为最优集结值矩阵;φ（A）为q个月份的综合评价值矩阵。

3 研究案例

武汉是我国中部地区最大的都市，也是重要的工业、科教基地和综合交通枢纽。近年来，经济发展势头强劲，2019年武汉市被列为新一线城市，GDP高达17157亿元。然而，随着经济的高速发展，与其他许多城市一样，近些年来武汉市的空气污染严重。由于其特殊地势、气象条件以及经济、能源消费增长的共同作用，导致武汉城市圈近年来以PM2.5为首要污染物的重污染天气现象频繁发生，已成为全国重要的大气污染城市之一。根据2016世界卫生组织发布的全球空气污染城市排名，在我国210个地级及以上城市中，武汉市在空气质量最差的城市中排名第12。其高密度的城市空间形态与严重的大气颗粒物污染，反映出大城市的典型污染特征。然而，自2020年1月23日至2020年4月8日，由于受到新型冠状病毒病（COVID-19）肆虐的影响，为了防止病毒向其他地区的扩散和疫情的进一步恶化，武汉市实行了前所未有的、最为严格的“封城”措施。这场突如其来的重大突发公共卫生事件，使得一个千万人口级的特大城市在较高速的经济发展中，骤然间被迫按下了经济的暂停键，2个多月时间内经济几乎处于停滞状态。为了考察武汉市自爆发COVID-19病毒以来，经济状况的改变对于当地空气质量的影响，本文根据武汉市空气污染特征，选择PM2.5、SO2、NO2为空气污染指标。以http：//aqicn.org/city/wuhan/cn/网站提供的武汉市2020年1月-2020年4月期间以及上一年的同期的主要空气污染物PM2.5、SO2、NO2监测日报数据为依据，利用本文提出的模型对其进行评估和对比分析。通过此案例的研究，揭示在经济停滞或负增長时对空气污染的影响规律。

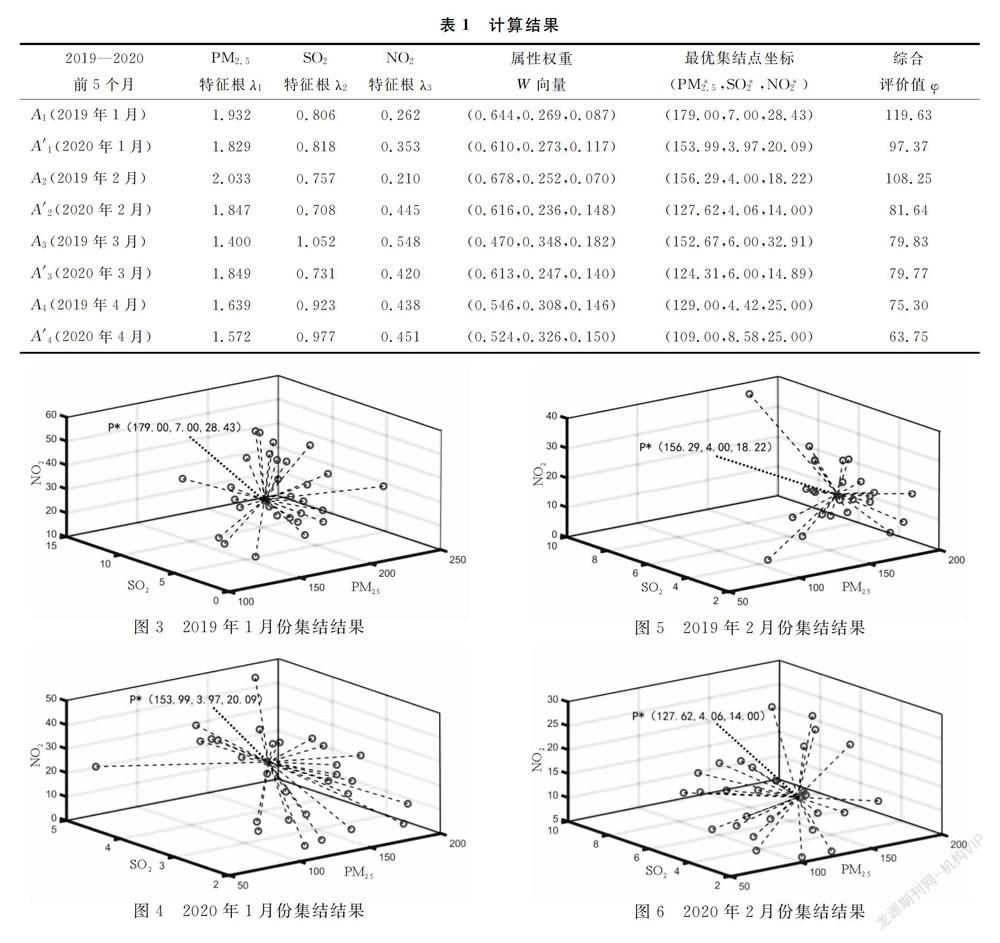
为了便于评估和比较，需要将日报数据集结为以月为单位的集结数据。根据公式（4），设定每日距离权重向量α=1。应用我们编制的PGSA_COMPILE程序，对武汉市2020年1月—2020年4月期间以及上一年的同期的主要空气污染物PM2.5、SO2、NO2监测日报数据进行最优集结。得到的最优集结坐标：P*（PM*2.5，SO*2，NO*2）即代表了每月空气污染指标数据，从而，可以构成最优集结矩阵R*，见图3-图10再根据公式（6）、（7）计算各指标属性权重向量W及综合评价值向量φ。其计算结果，见表1。

由于空气污染综合指标的评价值是越低越好，因此，由表1得出的比较结果为：

2020年前4个月比较：A′4（φ）A′3（φ）A′2（φ）A′1（φ）。

2020年前4个月与2019年同期比较：A′1（φ）A1（φ）;A′2（φ）A2（φ）;A′3（φ）A3（φ）;A′4（φ）A′4（φ）。

为直观形象起见，根据φ值绘制了折线图，见图11。图11表明，2020年的1月-4月的空气质量皆优于2019年的同期。这表明武汉市受到COVID-19病毒疫情影响而导致的经济停滞及下滑期间，空气质量明显高于正常年份的上一年同期，经济因素对于空气质量的影响显著。图9还表明，2020年1-4月φ值总体呈现下降趋势，即空气质量总体呈现向好的趋势。这与该市采取的史上最为严格的封城措施有关。

为了进一步考察武汉市封城期导致的经济停滞及下滑对空气主要污染物PM2.5、SO2、NO2的各自影响，不妨进行一下封城期间（2020年1月-2020年4月）与上一年同期各污染物的对比，见图12.、图13.、图14。

由于封城期间，经济活动处于基本停滞状态，因此，为考察单纯经济因素究竟会对各污染物产生多大影响提供了一次难得的经济学实验的机会。我们不妨建立如下公式：

Ei=PTi-PT′iPTi（8）

式中Ei为经济对于第i种污染物的影响度（i=1，2，3;1=PM2.5，2=SO2，3=NO2），PT′i为封城期间第i种污染物的均值，PTi为上一年同期第i种污染物的均值。

根据公式（8）就可以计算经济影响度：

EPM2.5=151.59-123.51151.59=19%

ESO2=5.56-4.925.56=12%

ENO2=27.21-13.9227.21=49%

计算结果表明，单纯经济因素对PM2.5的影响度为19%，对SO2为12%，对NO2为49%。这一结果也可以理解为，剔除单纯经济因素或增加经济因素可以使PM2.5、SO2、NO2分别减少或增加19%、12%、49%。单纯经济因素对于各污染物的影响程度大小依次为：NO2，PM2.5，SO2。除了单纯经济因素外，其他因素对PM2.5、SO2、NO2影响分别为：81%、88%、51%。

4 结语

本文在将平面Steiner-Weber点问题拓展为空间问题的基础上，创建了一个SOAM集结方法，并应用PGSA算法解决了将多指标属性的主要空气污染物日报数据集结成为月报数据难点问题。从而，可以通过线性加权方法计算各月的空气质量综合评价值φ，以此来评估每个月的空气质量。

应用SOAM方法对于武汉市2020年1-4月以及上一年2019年1-4月的各月主要污染指标的空气质量进行了研究评估。研究结果表明，2020年前4个月，在武汉市受到COVID-19疫情的影响迫使采取了停工、停产及封城措施后，经济处于停滞或下滑状态下，该市的空气质量则呈现出了明显的向好趋势。而且，与上一年正常年份的2019年同期相比，2020年前4个月的总体空气质量要优于2019年的同期。

由于封城措施使得该市的经济影响因素变量趋近为零，这为研究单纯经济变量对于空气质量的影响提供了一次极为难得的真实的实验研究。为了揭示这一奥秘，本文提出了一个经济影响度模型，与经济活动正常年份2019的同期进行比较研究，以得出各主要污染物的经济影响度。研究结果表明，单纯经济因素对PM2.5的影响度为19%，对SO2为12%，对NO2为49%。即剔除单纯经济因素或增加经济因素可以使PM2.5、SO2、NO2分別减少或增加19%、12%、49%。单纯经济因素对于各污染物的影响程度大小依次为：NO2，PM2.5，SO2。

除了单纯经济因素外，其他因素对PM2.5、SO2、NO2影响分别为：81%、88%、51%。这说明一个城市的经济因素对自身空气污染的产生只是一个重要的因素之一，但并非是唯一的影响因素。一个城市的空气污染程度，除了受到经济因素影响外，尚不能排除其地理位置、气候等自然因素以及其他省份和地区的输入性污染等影响。事实上，一个城市要维持正常的功能，经济活动是必不可少的，而经济活动也必然会导致一定程度空气污染的产生。因此，如何协调经济发展与污染之间的关系，走可持续发展之路，是城市所要面对的两难问题。

参考文献：

[1]BOULDING KE.The economics of the coming spaceship earth in environmental quality in a growing economy[M] Jarrett， H.， ED.; Resources for the Future/Johns Hopkins University Press： Baltimore， MD， USA，1966：3-14.

[2]LIU SH， HUA SB， WANG K， et al. Spatial-temporal variation characteristics of air pollution in Henan of China： Localized emission inventory， WRF/Chem simulations and potential source contribution analysis[J].Science of the total Environment，2018，624，396-406.

[3]LIU XP， ZOU B， FENG HH， et al. Anthropogenic factors of PM2.5 distributions in China's major urban agglomerations： A spatial-temporal analysis[J].Journal of Cleaner Production，2020，264：121709.

[4]MUEZZINOGLU A， ATIMTAY AT， INCECIK S. Special issue： Assessment of urban and regional air quality and its impacts-Selected papers submitted to the third international symposium on air quality management at Urban[J]，Environment International，2008，34（5） ： 579-579.

[5]KUKLA GA. Economic growth， international trade and air pollution： A decomposition Analysis[J]. Ecological. Economics，2009，68（5）：1329-1339.

[6]ARISTOTELOUS K. A re-examination of the empirical relationship between economic growth and air pollution[J].International Journal of Ecology and Development，2017，32（1）：1-16.

[7]OUYANG X， SHAO QL， ZHU X， et al. Environmental regulation， economic growth and air pollution： Panel threshold analysis for OECD countries[J].Science of the Total Environment，2018，657：234-241.

[8]SOUKIAZIS E，PROENCA S，CERQUEIRA PA.The Interconnections between renewable energy， economic development and environmental pollution： A simultaneous equation system approach[J].Energy Journal，2019，40（4）：1-23.

[9]URHIE E， AFOLABI A，  MATTHEW O， et al. Economic growth， air pollution and health outcomes in Nigeria： A moderated mediation model[J].Cogent Social Sciences，2020，6（1）：1-14.

[10]CIN B.An empirical analysis of asian countries' economic growth and environmental air pollution using dynamic MG panel model[J].Kukje Kyungje Yongu，2013，19（4）：89-112.

[11]GEORGIEV E， MIHAYLOV E. Economic growth and the environment： reassessing the environmental Kuznets Curve for airpollution emissions in OECD countries[J].Letters in Spatial and Resource Science，2015，8（1）： 29-47.

[12]TSUJIMOTO M. Economic growth and air pollution in the Persian （Arabian） Gulf States： Environmental Kuznets Curve hypothesis[J].Journal of the Japan Institute of Energy，2018，97（1）：16-22.

[13]楊旭，万鲁河，王继富，王宝健，徐洋.基于VECM模型的经济增长与环境污染和能源消耗关系研究[J].地理与地理信息科学2012，28（5）：75-79.

[14]XIE R， SABEL CE， LU X， et al. Long-term trend and spatial pattern of PM2.5 induced premature mortality in China[J].Environment International，2016，97：180-186.

[15]LU ZN， CHEN HY， HAO Y， et al. The dynamic relationship between environmental pollution， economic development and public health： Evidence from China[J].Journal of Cleaner Production，2017，166： 134-147.

[16]QIU F， WANG E， FAN M， et al. A questionnaire case study of Chinese opinions on the haze pollution and economic growth[J].Sustainability，2018，10（6）： 1-30.

[17]QIU F， WANG E， FAN M， et al. Examining the effects of socioeconomic development on fine particulate matter （PM2.5） in China's cities using spatial regression and the geographical detector technique[J].Science of The TOTAL Environment，2018， 619：436-445.

[18]SHI YB， ZHAO XX， JANG CL， et al. Decoupling effect between economic development and environmental pollution： A spatial-temporal investigation using 31 provinces in China[J].Energy and Environment，2019，30（5）： 755-775.

[19]ZHU LY， HAO Y， LU ZN， et al. Do economic activities cause air pollution  Evidence from China's major cities[J].Sustainable Cities and Society，2019，49： 1-10.

[20]XIE QC， XU X， LIU XQ. Is there an EKC between economic growth and smog pollution in China？ New evidence from semiparametric spatial autoregressive models[J].Journal of Cleaner Production，2019，220： 873-883.

[21]YANG Y， LAN HF， LI J. Spatial econometric analysis of the impact of socioeconomic factors on PM2.5 concentration in China's inland cities： A case study from Chengdu Plain Economic Zone[J].International Journal of Environmental Research and Public Health，2020，17（1）： 1-19.

[22]YAGER RR. On ordered weighted averaging aggregation operators in multicriteria decision making[J].IEEE Transactions on Systems， Man and Cybernetics，1988，18： 183-190.

[23]MORDUKHOVICH B， NGUYEN MN. Applications of Variational Analysis to a Generalized Fermat-Torricelli Problem[J].Journal of Optimization Theory and Applications，2011，148（3）：  431-454.

[24]KUPITZ YS， MARTINI H， SPIROVA M. The fermat-torricelli problem， Part I： A discrete gradient-method approach[J].Journal of Optimization Theory and Applications，2013，158（2）： 305-327.

[25]STREKACHINSKII GA， ORDIN AA. Computer optimization of Steiner-Weber networks by the gradient method[J].Journal of Regional Science，1976，12（5）：537-540.

[26]魯晓春，詹荷生.关于配送中心重心法选址的研究[J].北方交通大学学报，2000，24（6）：108-110.

[27]程珩，牟瑞芳.物流配送中心选址的重心法探讨[J].交通运输工程与信息学报，2013，11（1）：91-95.

[28]李彤，王春峰，王文波，宿伟玲.求解整数规划的一种仿生类全局优化算法-模拟植物生长算法[J].系统工程理论与实践，2005，25（1）： 76-85.

[29]李彤，王众托.模拟植物生长算法的原理及应用[J].系统工程理论与实践，2020，40（5）： 1266-1280.

[30]GUNEY K， DURMUS A， BASBUG S. A plant growth simulation algorithm for pattern nulling of linear antenna arrays by amplitude control[J].Progress in Electromagnetics Research B，2009，17（17）： 69-84.

[31]RAO RS， NARASIMHAM S. A new heuristic approach for optimal network reconfiguration in distribution systems[J].Journal of Applied Science， Engineering and Technology，2009，5（1）： 15-21.

收稿日期：2021-04-01

基金项目：教育部人文社会科学研究规划基金项目（17YJAZH041）

作者简介：李磊（1959—），男，黑龙江哈尔滨人，博士，教授，博导，研究方向：系统工程，E-mail：lilei59@jiangnan.edu.cn。